液态燃料熔盐堆三维动力学程序开发及验证
左献迪 程懋松 戴志敏
1(中国科学院上海应用物理研究所 上海 201800)
2(中国科学院大学 北京 100049)
液态燃料熔盐堆最早于20 世纪40 年代由美国橡树岭国家实验室(Oak Ridge National Laboratory,ORNL)设计、建造和运行,被第四代核能系统国际论坛选为6种第四代反应堆堆型之一。液态燃料熔盐堆使用高温熔盐作为燃料和冷却剂,具有高温、低压、高化学稳定性等特性,可应用于偏远地区发电、海水淡化、高温制氢等[1]。液态燃料熔盐堆与传统固态燃料反应堆不同,燃料熔盐在一回路中循环流动,一部分缓发中子先驱核(Delayed Neutron Precursors,DNP)在堆芯外一回路中衰变引起反应性损失,流场变化也会直接影响到反应性损失的多少,反应堆大部分能量直接释放在燃料熔盐中,中子物理与热工流体存在紧密耦合的关系。由于熔盐堆独特的中子动力学和热工流体特性,传统固态燃料反应堆堆芯动力学程序无法适用于液态燃料熔盐堆,需要重新推导模型和开发适用于液态燃料熔盐堆的动力学程序。
目前国内外已有许多团队进行了液态燃料熔盐堆计算模型和程序开发。中国科学院上海应用物理研究所Cheng等[2]基于OpenFOAM开发了适用于罐式液态燃料熔盐快堆的多物理耦合程序TMSR3D;施承斌、李锐等[3‒4]扩展RELAP5/Mod4.0 程序,使用点堆方程求解堆芯中子物理,添加零维和一维DNP计算模型,可进行熔盐堆系统瞬态分析。Shen 等[5]使用蒙特卡罗程序Serpent 对熔盐实验堆(Molten Salt Reactor Experiment,MSRE)进行了基准题验证。Krepel 等[6]基于固态堆三维节块法动力学程序DYN3D 发展了适用于熔盐堆的中子动力学与热工水力学耦合程序DYN3D-MSR。Li 等[7]基于格林函数节块法开发NTH3D-MSR。Zhuang 等[8]开发了节块法程序MOREL对MSRE建模并进行动力学分析计算。Jaradat 等[9]开发PROTEUS-NODAL,建模分析了MSRE 与熔盐快堆(Molten Salt Fast Reactor,MSFR)。
使用点堆模型无法对堆芯中子物理做详细计算分析,而蒙特卡罗法耗时较长。节块展开法计算速度快、可进行通量重构,广泛应用于核设计和动力学分析。中国科学院上海应用物理研究所开发了基于指数变换的三维四边形和六角形节块法动力学程序TCORE3D[10],可用于四棱柱和六棱柱形组件的熔盐冷却固态燃料熔盐堆三维时空动力学计算分析。
为开展液态燃料熔盐堆设计及分析,在TCORE3D 基础上,开发基于节块展开法的液态燃料熔盐堆三维动力学程序ThorCORE3D,并采用美国橡树岭国家实验室的MSRE稳态和瞬态实验基准题进行程序初步验证。
1 理论模型与数值方法
1.1 中子物理
液态燃料熔盐堆中燃料熔盐在一回路中循环流动,但熔盐的流动速度远小于中子速度,其对中子通量分布的影响很小,而DNP 会随燃料盐循环流动,轴向分布受流动效应影响明显[11],且会在堆外一回路中部分衰变造成反应性损失。程序采用三维时空多群扩散方程与包含对流项的一维缓发中子先驱核守恒方程,在节块n内:
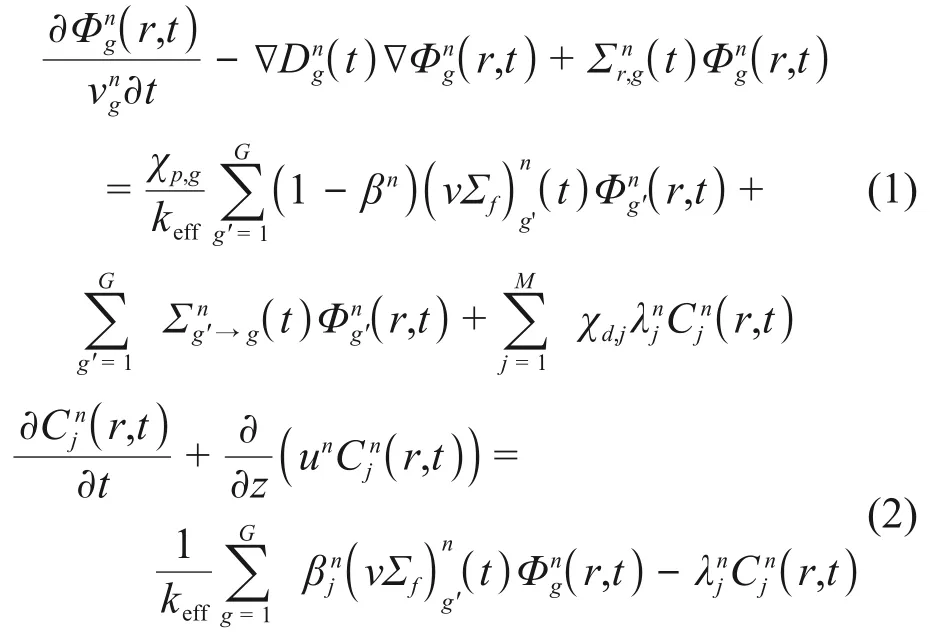
式中:g=1,2,…;G为中子能群编号;j=1,2,…;M为DNP群编号。为中子通量密度为DNP浓度;为DNP衰变常数;βn为缓发中子总份额为各群缓发中子份额;keff为有效增殖因子为中子速度;为扩散常数分别表示宏观吸收截面、宏观裂变截面、宏观散射截面;χp,g、χd,j分别表示瞬发中子、缓发中子能谱;un为燃料熔盐流速。
中子多群扩散方程采用节块展开方法求解[10]。
对于DNP守恒方程,假定在时间步长内指数变化进行时间离散,略去群角标:

采用一阶迎风格式进行空间离散:

最后整理为方程(5)、(6),通过迭代法求解。

在稳态计算结束后使用相同求解器,更换相应截面参数进行共轭方程求解:


式中:为共轭中子通量密度;为共轭DNP浓度。
求解完成后使用共轭中子通量密度等进行反应性、有效缓发中子份额、有效DNP衰变常数计算:



式中:ρ为反应性;βeff,j为有效缓发中子份额;λeff,j为有效DNP衰变常数。
1.2 热工流体
与传统固态燃料反应堆不同,液态燃料熔盐堆中大部分裂变能量直接释放在燃料熔盐中,流体能量方程中既有石墨的壁面换热源项,又有内热源。一回路燃料熔盐沸点较高不易汽化,直接采用单相流模型。通道式液态燃料熔盐堆燃料熔盐在各个通道中分别流动,相互之间不存在质量动量交换。ThorCORE3D 采用并联多通道模型进行热工流体(Thermal-hydraulic Fluid,HT)计算,将各种通道等效为同心圆柱。如图1 所示,通道内一维单相流热工流体动量、能量和质量方程如式(13)。

图1 热工流体计算通道近似Fig.1 Channel geometry approximation in TH calculation

式中:ρ为燃料盐密度;u为燃料盐流速;p为压强;h为燃料盐焓值;g为重力加速度;pfric为摩擦压降。
动量和质量方程采用差分法求解。焓方程采用特征线法求解,流体温度作为后续石墨温度求解边界条件。
求解石墨温度场时将石墨近似为内径r0外径R的空心圆管,外表面为绝热边界,内表面与燃料熔盐对流换热,忽略轴向导热。其热传导模型与固态堆中燃料棒传热模型类似,方程如下:

式中:T为石墨温度;ρg、cg、λg分别为石墨密度、比热容、热导率;Qv为石墨体积释热率。
石墨方程求解采用分层解析法,将石墨柱等面积均分为一系列同心圆管,通过输入定义各层释热份额,每个石墨管内均可解析求解出平均温度与壁面温度关系,进而推导出相邻石墨管平均温度关系,瞬态也可化为相同形式,采用三对角矩阵方法求解。
1.3 程序计算流程
ThorCORE3D 程序计算流程如图2 所示。计算前先由确定论组件程序或蒙卡程序生成不同温度、密度点的少群宏观截面。计算开始先假设均匀的功率分布,进行第一次热工流体计算,根据计算出的热工流体参数对截面数据进行插值更新,使用更新后的截面与流速等参数进行包含DNP 守恒方程的中子物理计算,根据中子通量结果计算出新的功率分布,多次迭代直到keff、温度等参数收敛。稳态计算结束后进行共轭通量计算。瞬态计算可在稳态计算完成后开始,同样迭代计算中子物理与热工流体,收敛后推进至下一时间步,直至计算完成。

图2 ThorCORE3D程序流程Fig.2 Flowchart of ThorCORE3D
2 程序验证
本节使用美国橡树岭国家实验室熔盐实验堆实验基准题开展ThorCORE3D 动力学程序初步验证。MSRE 是美国橡树岭国家实验室在20 世纪60 年代设计、建造和运行的第一个熔盐实验堆,是目前唯一可用的液态燃料熔盐堆实验数据来源。MSRE设计功率10 MW,实际运行功率8 MW,前期使用U-235燃料,后期使用U-233,其基本设计参数与材料物性如表1所示。

表1 MSRE主要参数Table 1 Key parameters of MSRE
使用ThorCORE3D动力学程序对MSRE进行建模,将整个堆腔等效为高200.67 cm 的圆柱,上下腔室高均为17.15 cm,堆芯活性区高166.37 cm,轴向共划分20节块,如图3(a)所示。堆芯径向每个燃料通道与周围石墨划分为一个正方形节块,每个控制棒通道与样品通道等效为4 个通道,径向共划分1 372 节 块,如 图3(b)所 示。使 用 组 件 程 序DRAGON生成计算所需的少群截面,DNP参数使用ORNL报告中数据,如表2所示。

表2 缓发中子先驱核参数Table 2 Parameters of DNP
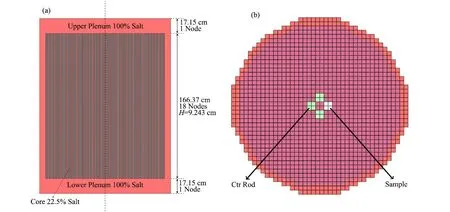
图3 MSRE轴向(a)和径向(b)节块划分Fig.3 MSRE axial(a)and radial(b)nodalization
2.1 稳态计算验证
使用MSRE 实验中流动引起的DNP 损失和控制棒积分与微分价值曲线开展ThorCORE3D 动力学程序稳态计算验证。
2.1.1 DNP损失
通过式(11)计算燃料流动与燃料静止状态下的有效缓发中子份额βeff,二者差值即为熔盐燃料流动引起的DNP 损失。如表3、4 所示,分别给出了采用U-235 燃料和采用U-233 燃料运行工况下,ThorCORE3D 计算值与MSRE 实验值、ORNL 计算值 及 其 他 程 序 计 算 值[7–8,18]对 比 结 果。ThorCORE3D 程序计算的DNP 损失与MSRE 实验值吻合良好,位于其他计算程序计算值范围内。使用ENDF 数据库DNP 参数与使用ORNL 报告中参数计算结果基本一致,后续计算均直接使用ORNL报告中DNP参数。
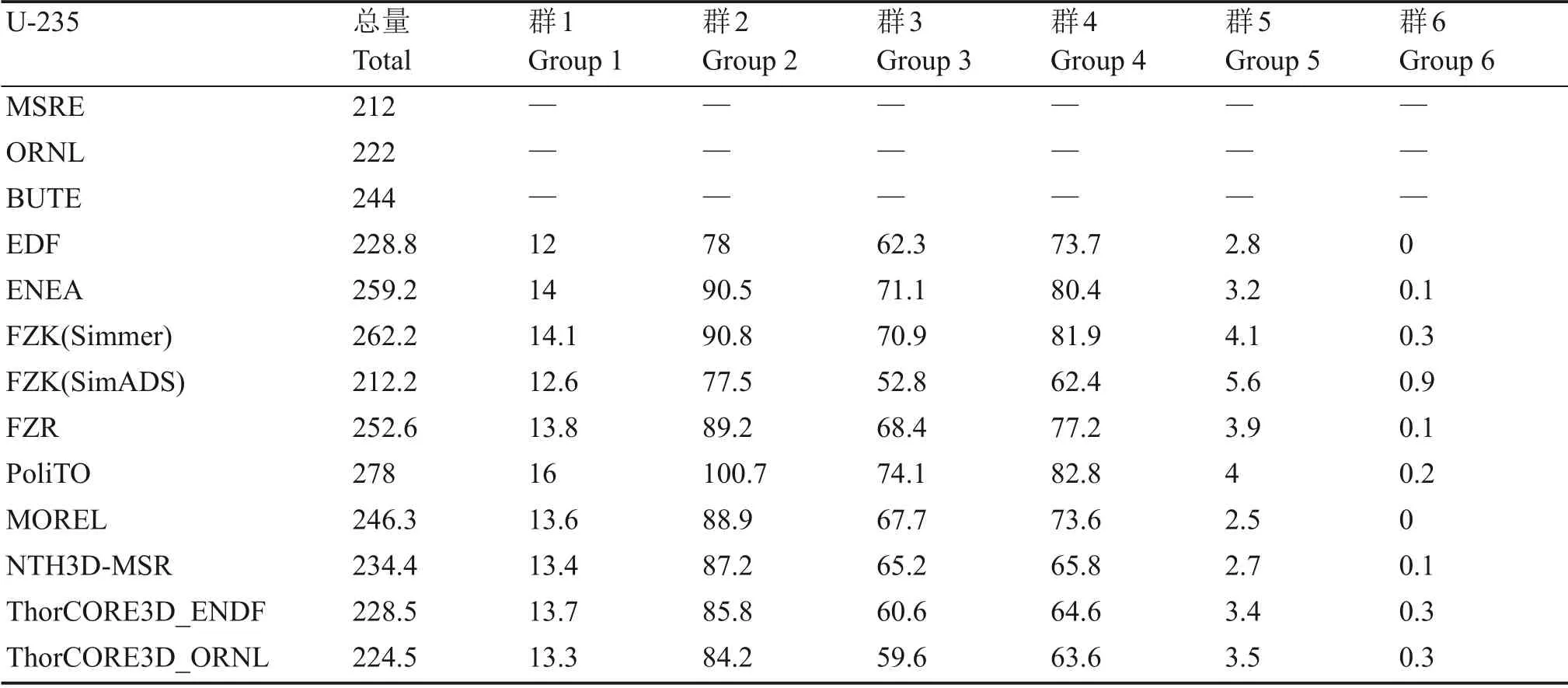
表3 使用U-235燃料正常运行下的缓发中子份额损失(10−5)Table 3 Loss in the delayed neutron fractions(10−5)due to the fuel circulation for U-235 fuel
2.1.2 控制棒价值
MSRE 共具有三根控制棒,实验中保持2 号、3号控制棒拔至顶端,测量1 号控制棒微分及积分价值[12]。使用ThorCORE3D 计算时,将1 号控制棒从完全插入状态逐级拔出至最顶端,共分14 个节点,计算每个位置处的keff,对比得出相应区间控制棒价值,并与MSRE 实验值对比。计算发现价值幅度与实验值基本吻合,但对应位置存在约10 cm 的整体偏移,其他研究者也发现相同现象[5]。纠正过后的控制棒积分价值对比如图4 所示,微分价值对比如图5 所示。结果表明:ThorCORE3D 程序计算的微分价值曲线相比实验值稍有轻微的偏移,这也造成了积分价值曲线在前段略微低于实验值,总的积分价值与实验值基本吻合。

图4 1号控制棒的积分价值Fig.4 Integral worth of control rod No.1
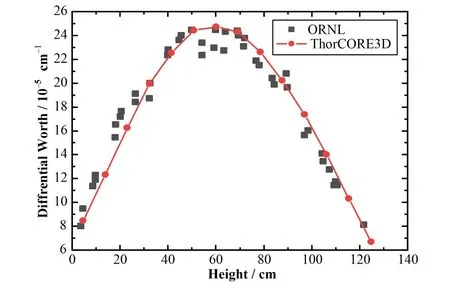
图5 1号控制棒的微分价值Fig.5 Differential worth of control rod No.1
2.2 瞬态计算验证
使用MSRE启泵、停泵、自然循环实验与引入反应性实验进行ThorCORE3D 动力学程序瞬态计算验证。
2.2.1 启泵和停泵实验
启泵和停泵实验是MSRE 零功率实验的一部分,实验过程中使用U-235 燃料。初始时刻一回路熔盐静止,在零时刻启动一回路熔盐泵,2 s 时熔盐开始流动至8 s时加速到额定流量,如图6所示。

图6 受保护启泵和停泵过程中燃料盐流量变化Fig.6 Fuel flow curve during transient of protected fuel pump startup and coastdown
由于燃料熔盐流出堆芯,部分缓发中子先驱核在堆芯外回路中衰变释放缓发中子,引起反应性损失。在一回路流量变化时,同时调节控制棒位,通过控制棒引入反应性使堆芯维持临界,记录控制棒位随时间的变化[12]。约15 s 后一回路中的DNP 随着燃料熔盐流动再次进入堆芯,损失的反应性随之降低,几次波动后逐渐稳定。停泵情形与启泵类似,在20 s内流量从额定值降低到零,记录棒位变化。

表4 使用U-233燃料正常运行下的缓发中子份额损失(10−5)Table 4 Loss in the delayed neutron fractions(10−5)due to the fuel circulation for U-233 fuel
由于堆芯功率较低且基本维持不变,使用ThorCORE3D动力学程序计算启泵和停泵实验时忽略温度反馈。通过搜索控制棒位使堆芯功率维持不变,可直接计算出控制棒位置变化,如图7所示。

图7 受保护启泵和停泵过程中控制棒棒位变化Fig.7 Change of control rod position during protected pump start-up and coast-down transients
启泵工况棒位曲线峰值比实验值略低,最终棒位与实验值一致。停泵曲线在实验中段略高于实验值,之后与实验值基本一致。通过控制棒价值曲线将棒位转化为反应性并与实验值及其他程序计算值对比[6,8],如图8、9所示,ThorCORE3D计算结果与实验值吻合良好,并优于其他计算程序。

图8 受保护启泵过程中控制棒补偿反应性Fig.8 Compensated reactivity during protected pump start-up transients

图9 受保护停泵过程中控制棒补偿反应性Fig.9 Compensated reactivity during protected pump coastdown transients
2.2.2 自然循环实验
在MSRE 自然循环实验中使用了U-233 燃料,堆芯初始功率4.1 kW,二回路泵正常运转,一回路泵保持关闭,仅靠自然循环驱动燃料熔盐流动,一回路流量极低。实验开始后逐步增加空气散热器散热量,使堆芯入口燃料盐温度降低,不使用控制棒进行控制,由于温度负反馈效应堆芯功率上升,继而堆芯出入口温差增大,自然循环流量上升,因流动引起的DNP损失也随之增加[13]。
使用ThorCORE3D 计算时,将入口温度变化与燃料盐流量变化作为输入,如图10 所示,计算堆芯功率随时间变化。如图11所示,在起始2 000 s内计算值与实验值有一些偏差。这是由于实际实验过程并不是从稳态开始[18],而ThorCORE3D 从稳态开始瞬态计算,其他时间功率随时间变化曲线吻合良好。

图10 自然循环实验中燃料盐流量与入口温度变化Fig.10 Changes of fuel mass flow rate and fuel inlet temperature in the natural circulation experiment

图11 自然循环实验堆芯功率变化Fig.11 Variation of core power in the natural circulation experiment
2.2.3 引入反应性实验
在MSRE引入反应性实验中,使用U-233燃料,一回路泵正常运转。在1 MW、5 MW 和8 MW功率水平下分别引入2.48×10−4、1.9×10−4和1.39×10−4反应性,堆芯功率急速上升,进而堆芯温度升高引起负反馈,随燃料盐流出堆芯的DNP 也增多,二者共同作用使功率提升减慢并在达到最高点之后逐渐下降至初始功率水平[19]。
计算时反应性均在1 s内引入,由于程序目前尚不能进行堆芯外部一回路热工流体模拟,入口温度使用RELAP5/Mod4.0程序计算值作为输入[4]。

图13 5 MW下引入1.9×10−4反应性后功率变化Fig.13 Power change in response to a step change in reactivity of 1.9×10−4 at 5 MW
计算结果与MSRE 实验值对比,如图12~14 所示。1 MW 和5 MW 工况下计算值与实验值吻合较好,8 MW 计算值在5 s 处比实验值多出一个尖峰,其他研究者计算值也有此峰[4],实验值记录的数据波动较大,此小峰可能被噪声淹没。
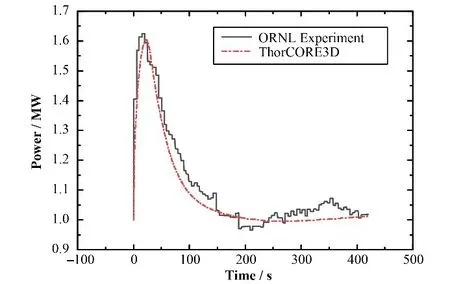
图12 1 MW下引入2.48×10−4反应性后功率变化Fig.12 Power change in response to a step change in reactivity of 2.48×10−4 at 1 MW

图14 8 MW下引入1.39×10−4反应性后功率变化Fig.14 Power change in response to a step change in reactivity of 1.39×10−4 at 8 MW
3 结语
液态燃料熔盐堆具有独特的物理和热工流体特性,传统固态燃料反应堆堆芯核热耦合程序不再适用。针对液态燃料熔盐堆核热耦合特点,基于节块展开法,建立了液态燃料熔盐堆三维动力学模型,并开发了相应的三维堆芯动力学程序ThorCORE3D,使用差分法进行带对流项的DNP输运方程求解,求解了带内热源的热工流体方程。采用美国橡树岭国家实验室MSRE 稳态和瞬态实验基准题,开展了ThorCORE3D 动力学程序初步验证。结果表明:在各种实验基准工况下,ThorCORE3D 动力学程序计算值与MSRE 实验值吻合良好,验证了改进后程序的正确性和适用性。ThorCORE3D堆芯三维动力学程序将为液态燃料熔盐堆概念方案、工程设计和瞬态分析提供强有力的工具。
作者贡献声明左献迪:进行程序开发及验证,数据分析及文章撰写;程懋松:提出研究思路,文章审阅与修订;戴志敏:负责研究方案指导、研究进度监督、研究项目管理和研究资金获取。

