基于小波变换的自适应阈值图像去噪技术研究
刘光宇 ,曹 禹 ,冯 伟 ,赵恩铭 ,邢传玺
(1.大理大学 工程学院,云南 大理 671003;2.哈尔滨工程大学 物理与光电工程学院,黑龙江 哈尔滨 150001;3.云南民族大学 电气信息工程学院,云南 昆明 650504)
1 引言
由于图像在传输和获取过程中会产生无法避免的噪声,且主要为高斯噪声,由此导致的图像质量下降,在后期处理图像过程中会增加难度,所以图像去噪是图像处理的关键[1]。
因为小波变换方法处理图像具有多分辨率且能量集中的性质[2],可以很好的区分图像中的噪声部分和不同频域的数据信息,很好的保留图像的真实信息,所以小波变换去噪结果优于一些传统的去噪方法[3]。利用小波变换对含噪图像处理得到对应的小波系数,处理小波系数需要选择合适的阈值将噪声信号和图像信号进行区分,重构信号的连续性和精准性对选择不同的阈值所产生的结果差异性比较大,所以选择合适的阈值来分离噪声和有效信号非常重要[4]。Donoho等人提出了小波软阈值估计方法和小波硬阈值估计方法[5]。然而,硬阈值法和软阈值法本身存在一些不足之处,如硬阈值法的阈值函数具有不连续性,重构所得的信号会产生伪吉布斯效应,软阈值方法估计后的小波系数和分解得到的小波系数总存在恒定的偏差,直接影响重构信号与有效信号的逼近程度[6]。为了保证图像的连续性和细节的保留,并提高图像的峰值信噪比(PSNR),基于小波变换的自适应阈值去噪技术可以通过噪声在小波变换下的特性自适应地确定小波分解的阈值,将PSNR作为滤波器参数的函数,采用缩小区间的搜索算法进行寻优,得到使PSNR最大的阈值函数参数,有效地去除了系统的噪声并达到较好的去噪效果[7]。
因此实验采用基于小波变换的自适应阈值去噪方法,与基于小波变换的软阈值函数、硬值阈值函数去噪方法的结果进行比较,验证基于小波变换的自适应阈值去噪技术的有效性。
2 小波变换图像去噪技术
2.1 小波变换图像去噪
基于小波变换的图像去噪技术首先通过小波变换将含噪的图像信号转换为一系列相应的小波系数。在这些小波系数中,有效信号对应的系数较大,噪声对应的系数较小[8],所以需要选择合适的阈值对小波系数处理,将噪声与有效信号分离,从而保留含有有效信号的小波系数,再通过小波逆变换得到去噪后图像[9]。小波去噪流程图如图1所示。

图1 基于小波转换的图像去噪技术流程图
设含噪图像模型 a(i,j)为:

公式中,a(i,j)为图像被噪声破坏后的含噪图像,b(i,j)为初始无噪图像;c(i,j)为遵从 N(0,σn2)的高斯噪声。
通过小波转换在等式两边同时进行后得到经过小波变换后的系数:

Wa为原始图像在小波变换后得到的系数,Wb为原始无噪声图像小波变换后的系数,Wc为高斯白噪声小波变换后的系数。

从(3)式可知,小波转换是一种线性变换,在选择阈值处理小波系数后,可以通过(4)式得到图像去噪之后的小波系数,而在实际去噪过程中,则直接通过阈值将噪声和有效信号分离。保留有效信号,舍弃噪声信号。
最后对Wb进行小波逆变换,就可以得到去噪之后重构的图像[10]。
2.2 阈值函数
在基于小波变换的阈值去噪方法中,阈值函数的选取主要有以下两种[11]:

(2)软阈值函数,函数如公式(5)所示。当小波系数的绝对值小于给定阈值时,将数值置为0,小波系数大于阈值时,令小波系数的值减去阈值,就可以得到去噪之后的小波系数。
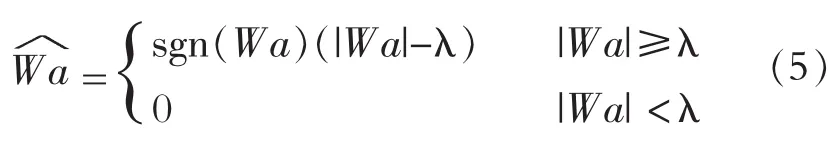
2.3 阈值选择
因为小波变换是将时空域上的信息变换到小波域上进行处理,经过小波变换产生的小波系数,将高频部分的噪声主要集中于小波系数较小的部分,而将低频部分的有效图像信号主要集中于小波系数较大的部分,因此需要选择合适的阈值对小波系数进行分离。
(1)Donoho和Johnstone提出的全局阈值方法
计算方法如公式(6)所示。

其中δ为噪声标准差,N为信号的长度。由于图像噪声信息的不明确导致无法计算δ,但可以通过估计噪声的方差σ,计算公式如(7)所示,median是求中值运算。

(2)Birge-Massart策略所选择的阈值[12]
计算方法如公式(8)所示。
首先设置一个分解层数x,针对所有大于x的层,我们不对其系数进行改动;对第y层(1≤y≤x),保留绝对值最大的ny个系数,ny由下式确定。

表达式内,经验系数可以通过Z和a表示。缺省的情况下,选用首层分解后的系数Z=L(1),a的大小在降噪时为:a=3。
2.4 自适应阈值函数理论
虽然通过软硬值阈值函数去噪结果相比较传统的去噪方法效果好,但是由于阈值函数中的阈值不可改变,因此不能动态调整阈值函数。而自适应阈值函数去噪公式如式(9)所示。

P为调节因子,P可以根据不同的小波系数大小进行动态调整,达到自适应选择阈值的目的,这样就可以解决软阈值函数去噪和硬阈值函数去噪的缺点,能够保证阈值函数的连续性,且避免阈值函数直接截断而引起的振荡效应,达到较好的阈值去噪结果表示通过自适应阈值处理后的小波系数,T表示为所运用的阈值[13-14]。
3 实验设计与实现
3.1 实验过程
实验图像为商洛学院校内路灯图像,首先将图像尺寸改为300×300像素的图像,并将图像类型转变为二值灰度图像,对该图像进行矩阵归一化处理,得到实验的原始图像,如图2所示。采用对比方法,对基于小波的自适应阈值去噪、软硬阈值去噪的结果进行比较分析。

图2 实验原始图像
3.2 实验结果
为了验证基于小波变换的软阈值函数、硬阈值函数与自适应阈值函数去噪技术的去噪效果,对原始图像添加方差为0.01的高斯噪声,得到含有噪声的图像,如图3(a)所示为含噪图像,再对含噪图像去噪,并对比分析结果。具体通过软阈值函数的Donoho全局阈值去噪方法,硬阈值函数的Donoho全局阈值去噪方法,软阈值函数的Birge-Massart策略计算阈值去噪方法,硬阈值函数的Birge-Massart策略计算阈值去噪方法以及自适应阈值函数的去噪方法进行去噪,去噪结果如图 3(b)到图 3(f)所示。

图3 去噪后图像
观察5种去噪结果,虽然图像中大部分噪声被滤除,图像变得更加清晰,达到较好的去噪效果,但在细节方面有比较大的差异。其中软阈值Donoho全局阈值、硬阈值Donoho全局阈值、软阈值Birge-Massart策略计算阈值去噪都对过度平滑,对物体边缘的轮廓不够准确,硬阈值Donoho全局阈值去噪和硬阈值Birge-Massart策略计算阈值去噪结果使图像出现锐化,而基于小波的自适应阈值去噪结果对物体边缘定位更加准确,清晰,且没有锐化等现象,达到了最好的去噪效果。
3.3 实验数据
对含噪图像去噪结果的客观评价主要比较峰值信噪比、均方误差和信噪比的数据,通过计算得到的数据如表1所示。

表1 不同去噪方法的评价指标结果

表1 不同去噪方法的评价指标结果(续)
通过表1数据,得到自适应阈值函数去噪方法的峰值信噪比和信噪比最大、均方误差最小,与自适应阈值函数去噪的图像结果最佳结论一致,实验数据证明了对高斯噪声降噪效果最好的是基于小波变换的自适应阈值函数去噪方法。
4 结语
对于图像去噪问题,利用基于小波变换的阈值函数去噪技术,对经过小波变换后的小波系数分别采用软阈值函数、硬阈值函数和自适应阈值函数对小波系数进行处理,最后通过小波逆变换实现了对图像的去噪。实验结果表明,基于小波变换的自适应阈值去噪方法对于图像的去噪结果可以达到最优,且峰值信噪比、均方误差和信噪比等数据都达到最佳,能够提升图像的整体质量,改善图像的视觉效果。

