基于时态软集的诺贝尔科学奖获奖数据分析

冯 锋，雒 静，王 谦，肖昀泽

(1.西安邮电大学 理学院,陕西 西安 710121;2.西安邮电大学 通信与信息工程学院,陕西 西安 710121;3.北京邮电大学 经济管理学院,北京 100876)

在“数据爆炸，知识匮乏”的大数据时代，海量的数据中存在很多的不确定性，这些不确定性信息直接影响人们在认知的过程中对现实问题的精确感知和预测。1999年，Molodtsov首次提出了经典软集的概念，为处理不确定性问题提供了新的研究方向[1]。从不同角度刻画同一复杂事物往往会得到其不同的侧面，而这些不完备的侧面都可以被视为对该复杂事物的近似描述，将这些近似描述综合起来即可构成对该复杂事物较完备的刻画。软集理论作为一种从参数化角度刻画不确定性问题的数学工具，引入对象论域和参数空间，能够实现更为客观且丰富的信息描述和处理，解决了概率论、模糊集[2]和粗糙集[3]等传统方法中参数化不足的问题。在实际应用中，也能够更灵活地处理复杂的不确定性问题，现已广泛应用于数据挖掘、决策分析和代数学等诸多领域[4]。

数据挖掘旨在从数据库中自动识别和提取出隐藏在其中的有价值信息，并将其表征为知识，进而提供辅助决策支持。关联规则挖掘是数据挖掘中最早活跃的一个重要分支，其目的是从交易数据集中提取频繁模式，并生成由频繁模式组合的强关联规则。Agrawal等[5-6]首次提出了关联规则的概念，并给出了关联规则挖掘问题的描述及具有代表性的Apriori算法。此后，还衍生了Apriori_LB[7]、XApriori[8]和基于权重的Apriori算法[9]等改进方法。Zaki等[10]提出了Eclat算法，这是一种基于垂直数据格式生成候选项集的深度优先算法，在挖掘过程中只需扫描一次数据库。随后也出现了Eclat的优化算法，如dEclat算法[11]和Eclat_opt算法[12]。FP-growth算法[13]是一种不产生候选项集的发现频繁项集的挖掘方法，其依赖于基于树的数据结构压缩存储有关频繁项集的数据信息。Aryabarzan等提出了一种有效的数据结构NegNodeset[14]，并基于此结构设计了negFIN算法，该算法采用集合枚举树生成频繁项集，并使用一种提升方法来修剪搜索空间。

传统关联规则挖掘是一种建立在事务数据集上的静态挖掘方法，而时态关联规则挖掘考虑到了传统关联规则挖掘所忽略的时间信息，旨在研究不同时段内有趣的关联规则，能够揭示潜藏在事物动态演进过程中的发展规律。Bettini等[15]研究了时间约束的事件结构粒度，发现了具有多粒度的频繁事件模式。孟志青[16]系统地研究了时态型和时态粒度的相关理论概念，并给出了一类简单频繁事件模式发现的例子。Ye等[17]提出了一种能够直接应用于时态数据集的关联规则挖掘算法。欧阳为民等[18]在Apriori算法的基础上进行扩展，提出了时间区间延展与归并技术以及新的时态关联规则发现算法，进一步推广了关联规则的应用。毛国君等[19]引入了时态区间代数，并给出了时态区间变量的时态交和时态并，提出了一种时态约束下的关联规则挖掘算法，用于挖掘基于时态约束的频繁项目序列集。臧国心等[20]研究了时态约束下各属性状态之间的周期时态关联规则，给出了相关描述语义及其实现算法。Gharib 等[21]利用时间粒度分层的概念解决了时间序列数据库动态关联规则的挖掘问题，开发了一种增量时态关联规则挖掘方法。Hong 等[22]提出了一个三阶段挖掘框架，可在时态数据库中找到具有分层粒度的时态关联规则。

2011年，Herawan和Deris首次将软集理论应用于交易数据集中的关联规则挖掘[23]。Feng等修正了文献[23]中的一些重要概念，并给出了参数陪集、参数类化软集和实现集等定义，进一步完善并阐明了基于软集的关联规则挖掘方法的本质[24]。之后，Feng等[25]提出了以软集理论和软集逻辑公式为主要工具描述和挖掘关联规则的新路线。此外，Feng等[26]给出了常规关联规则和极大关联规则挖掘中相关核心概念的统一数学表征，并提出了基于软集逻辑公式的极大关联规则挖掘算法。然而，某些项集在整个事务数据集的时间跨度中并不会频繁出现，但其在某些特定时间段内却是频繁的。上述基于软集的挖掘方法缺乏对项集时间因素的考虑，会忽略附加时间信息的项集关联性，遗漏部分有趣的关联规则。基于以上研究动机，拟借助时态软集进一步增强关联规则挖掘，尝试设计一种融合时态软集和Apriori算法的新方法提取促进型强时态关联规则，挖掘潜藏在时态信息中的数据关联性。此外，将所提算法应用于分析诺贝尔科学奖获奖数据，进一步验证方法的有效性。

1 软集理论

软集的本质是由给定参数集及其相应的集值映射构成的一个二元组，下面主要简述软集和时态软集的相关概念。

1.1 软集

设U为初始论域，与U内对象相关的全体参数构成集合E，称为参数空间，将(U,E)称为软论域。U的全部子集构成的类为U的幂集，记作P(U)。

定义1[1]二元组Ω=(G,B)称为U上的一个软集，其中B⊆E是软集Ω的参数集，G:B→P(U)是一个集值映射，称为Ω的近似函数。

对任一参数b∈B，由近似函数确定的子集G(b)称作软集Ω的b-近似集。

定义2[24]设Ω=(G,B)为论域U上的软集，u∈U，则称CΩ(u)={b∈B:u∈G(b)}为u在Ω中的参数陪集。

1.2 时态软集

定义3[27]设U为初始论域，有若干互不相交的时间段pi(i=1,2,…,n)构成集合P={p1,p2,…,pn}，则称映射τ:U→P是U上的时态粒化映射。

2 关联规则挖掘

关联规则挖掘旨在从交易数据集中发现数据项集之间潜在的、有意义的联系。一般而言，关联规则的挖掘分为两步：1) 找出所有满足最小支持阈值的频繁项集；2) 由频繁项集产生满足最小置信度阈值的强关联规则。

下面主要介绍常规关联规则和时态关联规则，对比发现时态在关联规则中的重要意义。

2.1 常规关联规则

假设项域I={i1,i2,…,i|I|}是给定交易数据中的全体项目之集，每条交易记录t都是I的一个非空子集。集合D={t1,t2,…,t|D|}包含所有交易记录，称为交易数据集。由I中若干项目构成的非空集合X称为项集，包含k个项目的项集称为k-项集。若X⊆t，则称交易记录t在D中支持项集X。

定义6[24]令D为一交易数据集，X为一项集，将D中由所有支持项集X的交易记录构成的集合称为项集X在D内的实现集，记作ΔD(X)，即

ΔD(X)={t∈D:X⊆t}

该实现集的基数|ΔD(X)|为项集X在D中的支持，记为SD(X)。给定两个互不相交的非空项集X,Y⊆I，形式表达式X⟹Y称为一个关联规则，其中，项集X与项集Y分别是规则的前件和后件。

定义7[24]关联规则X⟹Y在交易数据集D内的实现集ΔD(X⟹Y)定义为

ΔD(X⟹Y)=ΔD(X∪Y)

规则X⟹Y在D内的支持SD(X⟹Y)定义为

SD(X⟹Y)=SD(X∪Y)=card(ΔD(X⟹Y))

定义8[24]关联规则X⟹Y在交易数据集D内的置信度CD(X⟹Y)定义为

若式中SD(X)=0，则CD(X⟹Y)=0。

定义9关联规则X⟹Y在交易数据集D内的提升度LD(X⟹Y)定义为

若式中SD(X)·SD(Y)=0，则LD(X⟹Y)=0。

提升度可以衡量项集X和项集Y之间的相关性，当规则X⟹Y满足LD(X⟹Y)>1时，则代表项集X的出现促进了项集Y的出现，二者呈正相关，称规则X⟹Y为促进型关联规则。此外，LD(X⟹Y)值越大，项集X的出现对项集Y的出现带来的增益越高，二者相关性越强。为了在交易数据集中挖掘出有意义的规则，需要预先设置最小支持阈值a和最小置信度阈值b。当SD(X)≥a时，称项集X为频繁项集。而当规则X⟹Y满足SD(X⟹Y)≥a且CD(X⟹Y)≥b时，可称X⟹Y为强关联规则。

2.2 时态关联规则

部分项集在交易数据集的整个时间跨度中并不是频繁的，但在某些时间段内这些项集往往会频繁出现。因此，在不同时段内挖掘项集之间的关联性，可能会有意外的发现。下面具体阐明时态关联规则挖掘的相关基本概念。

令D为交易数据集，t∈D为交易记录，P={p1,p2,…,p|P|}为若干互不相交的时间段之集。若满足pt=τ(t)∈P，即交易记录t发生在时段pt内，则称pt是t的时段标记，并称T=(D,τ,P)为一个时态交易数据集。

定义10[27]令T=(D,τ,P)为一个时态交易数据集，且t∈D，Q⊆P。若有项集X⊆t，τ(t)∈Q，则称t在Q所辖时段内支持项集X。

定义11[27]令T=(D,τ,P)为一个时态交易数据集，Q⊆P，X为一项集，则T中项集X在Q所辖时段内的时态实现集为

定义12[27]时态关联规则X⟹QY在时态交易数据集T中的时态实现集定义为

定义13[27]时态关联规则X⟹QY在时态交易数据集T中的时态置信度定义为

定义14时态关联规则X⟹QY在时态交易数据集T中的时态提升度定义为

3 基于时态软集的关联规则挖掘

下面结合时态软集的相关理论和时态关联规则的基本概念，研究时态关联规则的软集描述方法及相应挖掘算法。

3.1 时态关联规则的软集描述

设U为初始论域，u∈U，若干互不相交的时间段构成集合P={p1,p2,…,p|P|}，Q⊆P。

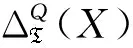
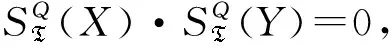
为了阐明上述概念在实际动态场景中的现实意义，下面以某医院患者的病例信息为例作简要论述。

例1假设某医院提供了12位入院治疗患者的相关信息，对这些病例数据进行统计，具体如表1所示。

表1 某医院12位患者的确诊信息

设入院治疗的12名患者ui(i=1,2,…,12)构成了论域U，与其相关的属性构成了参数空间E。令参数集B=A∪D⊆E，其中A={a1,a2,a3}为患者所患疾病，am(m=1,2,3)分别表示新冠肺炎、普通感冒和流行性感冒。D={d1,d2,…,d7}表示临床症状，其中dn(n=1,2,…,7)分别代表发热、咳嗽、咽痛、呼吸困难、乏力、腹泻和头痛。令P={p1,p2,p3}，其中pk(k=1,2,3)分别表示患者的确诊时间为“2022年1月14日”“2022年1月16日”“2022年1月17日”。

由表1构建时态粒化映射τ:U→P，该映射基于时态信息给出论域U的划分为

{τ-1(pk)|pk∈P}={{u1,u2,u3,u4,u5},
{u6,u7,u8},{u9,u10,u11,u12}}

在此基础上，进一步构建U上的一个时态软集Φ=(F,B,τ,P)，如表2所示。

表2 时态软集Φ=(F,B,τ,P)的表格表示

令Q={p1,p2}⊆P，由定义5易见

τ-1(Q)={u1,u2,…,u8}

记时态软集Φ的Q-片段软集为ΦQ=(H,B)，计算可得

H(a1)={u1,u3,u4,u6,u8}
H(a2)={u2,u7}
H(a3)={u5}

此外，

H(d1)={u1,u2,u3,u4,u5,u6,u8}
H(d2)={u2,u4,u6,u7,u8}
H(d3)={u2,u3,u6,u7}
H(d4)={u4,u8}
H(d5)={u1,u4,u6,u8}
H(d6)=∅
H(d7)={u5}

根据定义15，项集{a1}的Q-实现集为

考虑时态关联规则{a1}⟹Q{d1,d4,d5}，由定义16，其在时态软集Φ中的Q-实现集为

其Q-支持为

由定义17，该规则的Q-置信度为

根据定义18可得其Q-提升度为

取α=2和β=30%，则{a1}⟹Q{d1,d4,d5}是Q所辖时段中的促进型强时态关联规则，其含义可解释为2022年1月14日和16日这两天，被确诊为新冠肺炎的患者中有40%的人临床症状表现为发热、呼吸困难和乏力。

3.2 基于时态软集的关联规则挖掘算法

Agrawal等提出的Apriori算法[6]是一种经典的候选项集生成法算法，采用逐层搜索的方法筛选频繁项集，进而由频繁项集生成满足置信度阈值的强关联规则。下面，基于时态关联规则的软集描述，提出一种融合时态软集和Apriori算法的促进型强时态关联规则挖掘算法(Apriori-based Soft Promotive Temporal Association Rule Mining，Apriori-SPTARM)。

Apriori-SPTARM算法以时态交易数据集T=(D,τ,P)、集合Q⊆P、最小时态支持α∈N*和最小时态置信度β∈(0,1]作为输入，其输出为所有促进型强时态关联规则构成的集合SPTAR(T,Q,α,β)。算法的具体步骤如下。

步骤4连接剪枝，生成(k+1)-候选项集，并保留所有(k+1)-频繁项集。

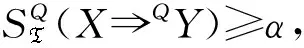
4 实例验证及结果分析

为了验证Apriori-SPTARM算法的有效性，将其应用于诺贝尔科学奖的部分获奖数据，分析特定时段内项集的关联性，对比该方法与常规关联规则挖掘方法的不同及其相较于传统方法的优势。

4.1 数据介绍

诺贝尔奖旨在表彰在化学、物理学、生理学或医学、和平以及文学领域作出巨大贡献的个人或组织，在国际上具有广泛而深远的影响。

在Kaggle网站中获取有关诺贝尔奖获奖者的数据集，该数据集共包含969条记录，涉及1901年至2016年所有获奖者的相关信息，包括获奖者姓名、性别、获奖年份、奖项类别和所属国家等内容。为简化问题，在此仅分析科学领域的获奖数据，包括诺贝尔化学奖(Nobel Prize in Chemistry,NPC)、诺贝尔物理学奖(Nobel Prize in Physics,NPP)和诺贝尔生理学或医学奖(Nobel Prize in Physiology or Medicine,NPPM)，并将诺贝尔科学奖简称为诺奖。对原始数据集进行数据清洗以达到分析需求，完成预处理后，人工添加2017年至2020年的获奖信息，最终得到满足条件的简化数据337条，仅包含获奖年份、奖项类别和所属国家等3类属性，可将每条记录视为一条交易数据。预处理后的部分获奖记录如表3所示。

表3 预处理后的部分获奖数据

4.2 数值实验

实验配置为Windows 10 x64操作系统、 Intel(R) Core(TM) i5-7200U CPU @ 2.50 GB处理器和8.00 GB内存，软件为Matlab R2019a。

设论域U={u1,u2,…,u337}包含1901年—2020年颁发的所有诺贝尔科学奖，与诺奖相关的属性构成U对应的参数空间E。取参数集B=C1∪C2，其中C1={c1,c2,…,c30}为诺奖的所属国家，C2={NPC,NPP,NPPM}。根据表3中的数据，令P={p1,p2,p3,p4,p5,p6}，其中p1=[1901,1920]，p2=[1921,1940]，p3=[1941,1960]，p4=[1961,1980]，p5=[1981,2000]，p6=[2001,2020]，即主要研究P所辖的6个时段。时态粒化映射τ:U→P可诱导出U划分为

{τ-1(pk)|pk∈P}=
{{u1,…,u52},…,{u278,…,u337}}

表4 时态软集=(G,B,τ,P)中参数集的支持

利用表4构建模糊集

直观地，基于预处理后得到表3中的简化数据，模糊集F能够描述每个国家的总体科学影响力，可将其称为总体科学影响力模糊集(Overall Scientific Impact Fuzzy Set,OSIFS)。筛选出支持不小于12的8个主要国家，通过计算得到的隶属度分别为

F(c1)=F(USA)=0.531
F(c2)=F(UK)=0.226
F(c3)=F(Germany)=0.125
F(c4)=F(France)=0.080
F(c5)=F(FRG)=0.056
F(c6)=F(Switzerland)=0.056
F(c7)=F(Japan)=0.047
F(c8)=F(Sweden)=0.045

根据总体科学影响力模糊集F的隶属度降序，8个国家的排名为

c1c2c3c4c5=c6c7c8

由此可见，美国的总体科学影响力位居第一，英国次之，排名第三的是德国。根据隶属度的相关含义，上述排名从诺贝尔科学奖的总体获奖情况角度反映了各国的科学影响力。

图1和图2给出了8个主要国家在6个时段中的隶属度计算结果，能够从获得诺贝尔科学奖的角度反映各国在不同时期科学影响力的变化情况。

图2 国家cj(j=5,6,7,8)在各时段的隶属度

根据隶属度的相关含义，由图1和图2可以看出，1901—2020年美国的科学影响力稳步提升，与此同时，德国的科学影响力逐渐下降，而英国则长期处于稳态。进入21世纪后，日本在科技领域发展较快。

4.3 结果分析

基于已构建的时态软集，利用Apriori-SPTARM算法提取6个时段内满足阈值条件的促进型强时态关联规则。将每个时段内的最小时态支持α设置为2和最小时态置信度β为70%，最终结果如表5所示。

表5 时态软集=(G,B,τ,P)中的时态关联规则

续表5 时态软集=(G,B,τ,P)中的时态关联规则

1) 考虑促进型强时态关联规则R1，其p1-支持为

p1-置信度为

p1-提升度为

该规则的实际意义可解释为1901—1920年间，授予荷兰的诺贝尔科学奖均为物理学奖。

考虑规则R4，其p2-支持为

p2-置信度为

p2-提升度为

该规则的实际意义可解释为1921—1940年间，授予荷兰的诺贝尔科学奖均为生理学或医学奖。

2) 考虑规则R9，其p4-支持为

p4-置信度为

p4-提升度为

该规则的实际意义为1961—1980年间，授予英国的诺贝尔生理学或医学奖有71.43%是与美国共享的。

再考虑规则R23，其p5-支持为

p5-置信度为

p5-提升度为

该规则的实际意义可解释为1981—2000年间，授予加拿大的诺贝尔化学奖均是与美国共享的。

对于规则R27，其p6-支持为

p6-置信度为

p6-提升度为

该规则的实际意义可解释为2001—2020年间，授予日本的诺贝尔化学奖均是与美国共享的。

可以发现，从1961年至今，各国在科技创新上的合作共享逐步加强。

3) 令Q=P={p1,p2,…,p6}，设置Q所辖时段内的最小支持为12，最小置信度为70%。对于规则{NPPM}⟹Q{USA}，其Q-支持为

Q-置信度为

Q-提升度为

利用常规关联规则挖掘方法，在1901至2020年整个时间范围内，规则{NPPM}⟹Q{USA}是频繁出现的但并不满足置信度阈值，故该规则不可被识别为强关联规则。而根据表5，规则R7({NPPM}⟹p4{USA})、规则R16({NPPM}⟹p5{USA})分别在时段p4和p5内被识别为促进型强时态关联规则。

再考虑规则{NPC,UK}⟹Q{USA}，其Q-支持为

Q-置信度为

Q-提升度为

因此，在传统挖掘技术中，该规则在1901—2020年整个时间范围内不是频繁的，更不可被识别为强规则。根据时态信息划分数据集后，对于规则R28，即规则{NPC,UK}⟹p6{USA}，其p6-支持为

p6-置信度为

p6-提升度为

显然，规则R28为p6时段内的促进型强时态关联规则，而借助传统方法这条规则不可被发现。

由上述分析可知，某些项集只在特定的时间段内是频繁出现的，而在整个数据集的时间跨度上并非是频繁的，借助传统方法不能提取出由这些频繁项集生成的规则。此外，部分频繁出现的规则不能满足最小置信度阈值，将数据集按时态粒度划分后，这些规则可被识别为某些时段内的强规则。总之，基于时态软集的关联规则挖掘方法可以帮助发现一些在常规关联规则提取中被忽略的强时态关联规则。

5 结语

探索了时态软集及其在时态关联规则挖掘中的应用。首先，借助时态粒化映射引入了时态事务数据集的粒度结构，定义了时态软集及其Q-片段软集，进而构建描述和挖掘时态关联规则的一种数学框架。其次，通过融合时态软集和Apriori算法，设计了一种基于时态软集的关联规则挖掘算法Apriori-SPTARM，可用于提取促进型强时态关联规则。最后，将所提方法应用于分析诺贝尔科学奖获奖数据。数值实验表明，在实际场景中数据会随时间产生动态变化，传统关联规则挖掘忽略了时间因素的影响，容易遗漏某些特定时段内的强规则。Apriori-SPTARM算法弥补了传统方法的缺陷。通过时态软集引入数据集的时态粒度结构后，局部时段内由频繁项集生成的规则可被识别为强时态关联规则。这为解决时态关联规则挖掘问题提供了新思路，同时也拓展了软集在关联规则挖掘中的应用。

值得注意的是，基于时态软集的关联规则挖掘中仅考虑了数据的时态粒化，且实例分析中采用了等时间间隔的划分方式，具有一定的局限性。在今后的研究中，可考虑自适应时段划分方法。此外，如何通过更具一般性的粒化方法划分事务数据集也是值得探索的方向。