向量格中Hahn-Banach定理的推广

刘和英

(合肥科技职业学院 基础部,安徽 合肥 230000)

2003年S.Simons在文[1]中介绍了 Hahn-Banach定理的一种新版本,并且给出它在线性或者非线性分析,凸分析以及单调多值函数等方面的若干应用,取得了一系列有意义的研究成果.本文主要考虑向量格中的Hahn-Banach定理,得到了线性算子扩张的一般结果,推广了S.Simons在文[2]中的若干结论,下面我们仍采用文[1]的一些记号和定义.

1 基本概念

定义1[3]若对∀x,y∈E,上确界sup(x,y)存在,记为x∨y,则序向量空间E称为向量格；若E是向量格,E0是E的子空间,若对∀x,y∈E0都有x∨y∈E0,则称E0是E的子格；如果对于E中每个非空的有上界的子集都有上确界,则称向量格E是序完备的.

定义2[3]设E是非平凡的向量空间,F是序完备的向量格,若映射S:E→F满足：

(1)S(x+y)≤S(x)+S(y).∀x,y∈E.
(2)S(λx)=λS(x).∀x∈E且λ>0.

则称S是一个次线性算子.

定义3[2]设E是非平凡的向量空间,F是序完备的向量格,且S:E→F是次线性算子,令A是E中的非空的凸子集,若映射g:A→E满足：对∀x1,x2∈A,u1,u2>0且u1+u2=1,都有

S(x+g(u1x1+u2x2))≤S(x+u1g(x1)+u2g(x2))

则称g是S-凸的.显然仿射算子一定是S-凸的,反之不成立.

引理1[3]设E是非平凡的向量空间,F是序完备的向量格,且S：E→F是次线性算子,则对任意的线性算子T0:E0→F满足T0x0≤Sx0,对∀x0∈E0且E0⊂E,则存在T0的扩张T:E→F,使得Tx≤Sx,∀x∈E.

以上引理1被称为向量格中的Hahn-Banach定理,下面通过证明得到了线性算子扩张的一般结果:

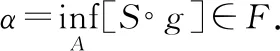
证明：显然T满足正齐性,下面只需证T是次可加.

[S(x1+λ1g(a1))-λ1α]+[S(x2+λ2g(a2)-λ2α)]=S(x1+λ1g(a1)+x2+λ2g(a2))-(λ1α+λ2α)=

将上式两边同取下确界,可得T(x1)+T(x2)≥T(x1+x2) 因此T是次可加的,从而T:E→F是次线性算子.现在固定a∈A,对∀x∈E,λ>0,由于

T(x)≤S(x)+λ[S(g(a))-α]

令λ→0则有T(x)≤S(x),综上存在E上的线性算子T,使得T≤S∀x∈E.

注:文[2]中的引理1.4是我们引理2取F=R时的特殊情况.

2 主要结果

推论1[2]设E是非平凡的向量空间,F是序完备的向量格,且S:E→F是次线性算子,则存在E上的线性算子T,使得T≤S.

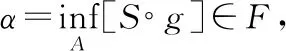
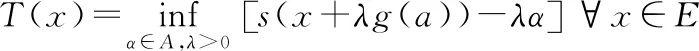
显然T:E→F是一个次线性算子,满足T≤S.再根据推论1,存在E上的线性算子L,使得L≤T.

因此有L≤S且-L≥-T,从而对∀a∈A,取λ=1,x=-g(a)我们有

L(g(a))=L(-g(a))≥-T(-g(a))≥α

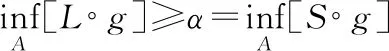
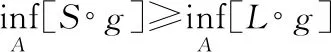
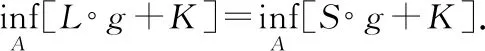
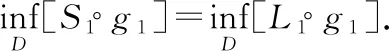
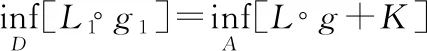
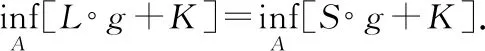
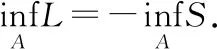
证明：令g(x)=x对∀x∈A,则结论显然成立.