基于改进样本块匹配准则的数字图像修复方法

张园园

(安徽工业经济职业技术学院 计算机与艺术学院,安徽 合肥 235100)

随着互联网的飞速发展,有关图像信息的交流和互动已经成为当今人们获取信息和传递信息的重要依据,人们日常生活中图像信息必不可少[1].但是图像信息在传输过程中会出现一些损坏以及一些人为的破坏,导致图像出现污迹和划痕；且拍照时不注意而拍入镜头的物体、人物以及拍照时留下的时间和文字信息,导致图像不美观[2,3].因此,图像修复问题是当今人们重视的问题,尤其是艺术价值和收藏价值较高的图像修复问题具有更高的研究价值.图像修复最早起源于古文物书画等作品的修复,且修复过程采用手工完成.但手工修复非常耗费精力和金钱,也隐藏很大的风险,会造成不可逆的结果[4-6].因此,当前通常采用数字化的数字图像修复技术,利用特定的算法确定待修复区域,并依据有效的匹配规则,完成图像修复,确保修复图像达到原图的视觉效果[7,8].本文采用基于改进样本块匹配准则的数字图像修复方法,提高修复图像的质量.

1 数字图像修复研究

1.1 采集最佳目标匹配块

采用Criminisi算法进行待修复图像板块优先权的确定,设置H为整个图像；Δ为等待修复区域；αΔ为待修复区域轮廓；α为已知像素区域,且α=1-Δ；Q为轮廓中心的目标点,待修复图像板块优先权设定为：

Q(q)=B(q)O(q)

(1)

式(1)中：采用置信度项B(q)对目标块Υq中准确信息进行评定,得出：

(2)

将B(q)初始化后,得出：

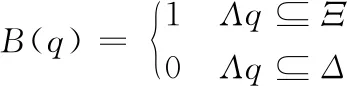
(3)

数据项O(q)表示每次迭代轮廓αΔ前沿的等照强度函数：

(4)

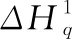
(5)

σΔ的单位外法线方向为uq,归一化因子为φ,值为255.

为了获取最大优先级的匹配块Υn,应在找到最大优先权的目标块Υq后通过匹配准则对所在的已知区域中进行搜索,两种匹配块匹配准则为：

(6)

式(6)中的Υq和Υn相对的已知像素点RGB的误差平方和(SSD)用o(Υq,Υn)表示如下：

(7)

其中,Υq及Υn中已知像素点分别对应式中的s及k,Υq中像素点φ的RGB三原色分别为V(s)、F(s)、K(s)；Υn中像素点k的RGB三原色分别为V(k)、F(k)、K(k)；因此,可以通过以上方法找到最佳目标匹配块.

1.2 基于IG-GN算法的图像修复方法

IG-GN算法是用于模板图像及目标图像的高效配准方法.由于将一种简单同时不实用的平方差及(SSD)相关准则运用在最初的IG-GN算法中,使得图像潜在的亮度变得非常敏感.该种情况使得任何可能的移位和缩放变化在目标图像中都会引起很大的误差[9],导致匹配块和目标块产生一定的变形差异[10].因此,本文采用一种能够接受图像块之间存在的潜在变化且融合了仿射变换函数的鲁棒性高且实用的相关准则,即ZNSSD准则,其表示如下：

(8)

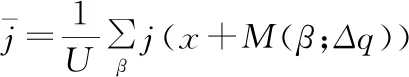
(9)

(10)

IG-GN算法采用的零均值归一化平方差与ZNSSD相关准则更加具备实用性,亮度的线性转变可以在目标图像中出现[11],且算法的精准度会增加.上述图像修复效果更加适合常规视觉标准,是因为它在图像修复中,能够明显减少图像块之间的差异[12].

最小化ZNSSD相关准则BZNSSD(Δq)是IG-GN算法的运算目标.通过将泰勒级数将式(8)展开后得出图像形变增量Δq为：

(11)

(12)

(13)

结合式(12)、(13)可以看出,这两个都是只与对照图像有关的常数,且都可以通过预计算得出.为得出最终的形变增量结果,采用最小二乘法最小化公式(11)中BZNSSD(Δq),则有：

(14)

式(14)中海森矩阵N6×6表示如下：

(15)

通过式(15)可以看出,只对照图像的局部梯度值、参考形变函数的雅可比矩阵的海森矩阵,与形变参数p不相关,其是迭代计算中的常数,能够通过预计算得出.该种运算过程忽略了海森矩阵的循环运算以及求逆过程,使得IG-GN算法运算效率大大提高.

形变参数增量Δq通过以上计算得出,因此也确定了对照图像的形变函数增量M(β;Δq).作用在目标图像的新形变函数,需要对形变函数增量求逆矩阵同时组合即刻形变函数M(β;q),采用公式(16)修正M(β;q)：

(16)

式(16)中形变函数增量的求逆操作为M-1(β;Δq),由此获取修正后的形变函数M(β;q).

IC-GN算法进行收敛迭代运算过程中,为使形变函数达到形变参数增量是零或者迭代次数达到预设最大次数[13],采用式(14)对当前形变函数下的形变参数增量进行反复计算且修正来完成,则设置收敛规范是形变参数增量的模值不大于0.001,相应的定义公式为：

(17)

基于IC-GN算法的图像修复详细流程如下：

(1)方法初始化.采用Criminisi算法获取最佳目标匹配块,设置对照图像以及目标图像分别是待修复图像块以及最佳目标匹配块,初始形变参数是两个图像块的相对位置偏差[14].通过式(12)到(15)运算出对照图像的梯度值、形变函数的雅克比矩阵以及海森矩阵后,进行高斯牛顿迭代法的运算.

(2)形变的目标图像块j(x+M(β;q))通过双三次插值算法得出.

(3)形变参数增量Δq根据优化算法与式(14)得出.

(4)利用式(14)获取形变参数增量Δq,依据Δq可获取形变函数增量M(β;Δq),为了获取修正的形变函数,需要将M(β;Δq)同前期的形变函数融合,并采用式(16)描述的修正方法进行修正M(β;q).

(5)将式(17)作为修复算法的收敛规范,循环执行过程(2)到(4)直到满足收敛规范.

(6)将获取最佳形变函数作用在目标图像中,通过该结果对待修复图像块中的未知像素进行填补[15],完成图像修复.

2 实验分析

为了对本文提出的基于改进样本块匹配准则的数字图像修复方法的有效性进行验证,对比分析本文方法和Komodakis方法的修复结果.所有实验均在windows10平台上采用Visual Stu dio 2017完成,计算机配置为IntelCoreTMm3-8100Y CPU@1.1.GHz 1.6GHz、RAM 4GB.

采用Komodakis方法和本文方法对图1进行修复,修复结果分别用图2和图3表示.

图1 待修复图像

图2 Komodakis方法去除修复效果

图3 本文方法去除修复效果

对比分析图1—图3三个图可以看出采用Komodakis方法进行修复后,图像较为模糊,而使用本文方法后,图像更清晰,没有明显模糊区域,证明了本文方法修复效果更好.

分别采用Komodakis方法和本文方法对图4中的白色污染区域进行修复,两种方法的修复结果分别用图5和图6描述.

对比分析图4—图6三个图能够明显看出,通过Komodakis方法修复后,白色污染的修复区域明显存在边界纹路,而通过本文方法针对白色污染区域进行修复后,修复区域不存在边界纹路,有效降低修复后的图像边界上像素值跳跃现象,确保修复后的图更接近原图或者达到原图,修复效果好.

对比分析两种方法的图像修复质量以及修复后图像峰值信噪比,结果分别用图7和表1描述：

图4 待修复图像

图5 Komodakis方法修复效果

图6 本文方法修复效果

从图7中能够直观看出,相对于Komodakis方法,本文方法对于天空图和枫叶图分别进行全图修复和区域污染修复后的图像质量更好,本文方法具备更好的修复能力.

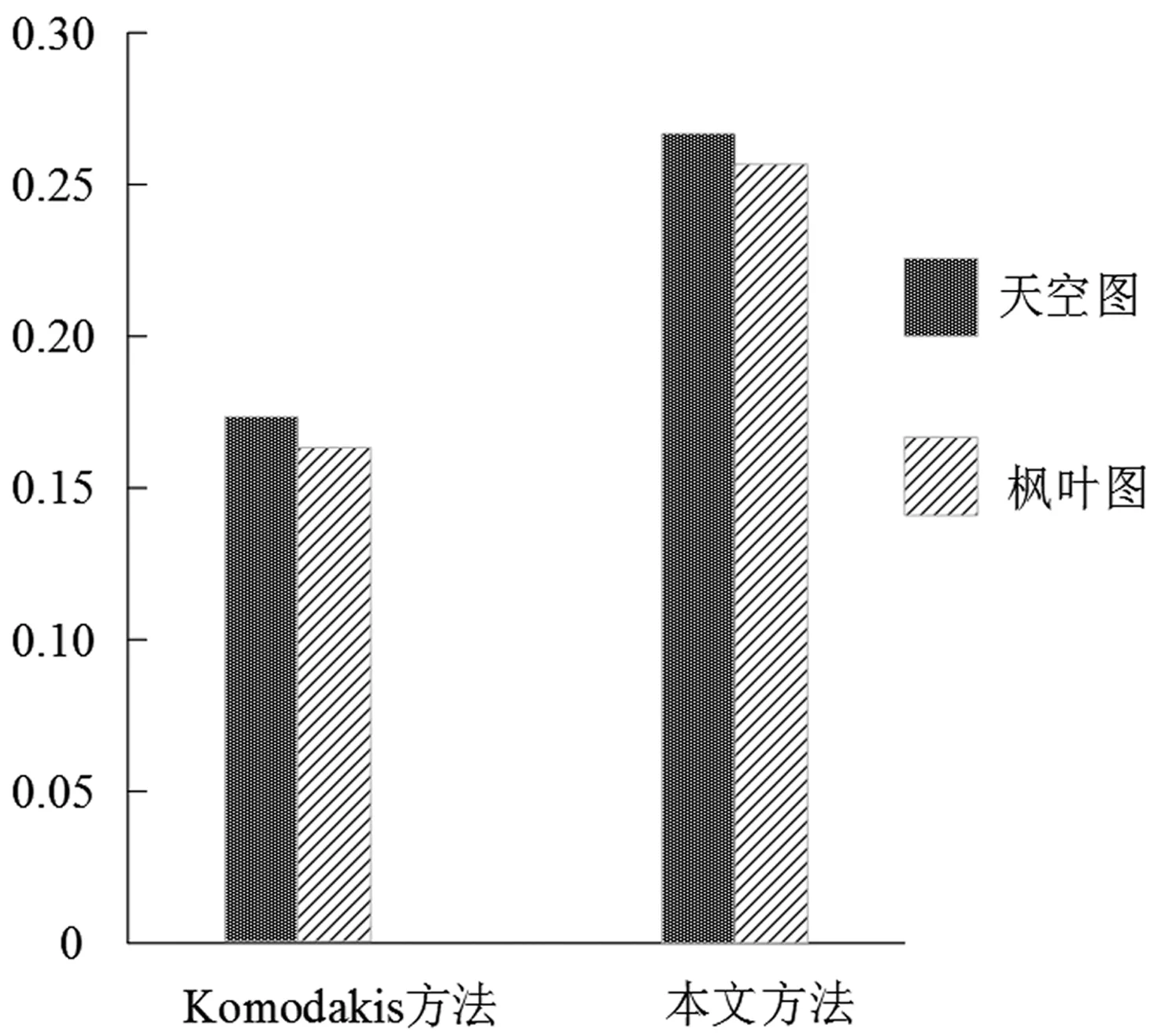
图7 图像修复质量对比

通过表1可以看出,本文方法修复后的图像峰值信噪比低于Komodakis方法的峰值信噪比,说明本文方法修复后的图像含噪少,图像清晰度好.

3 结 论

文章研究的基于改进样本块匹配准则的数字图像修复方法,将最小化ZNSSD相关准则作为样本块匹配准则,依据该准则采用IG-GN算法修复数字图像.该种算法采用的最小化ZNSSD相关准则具有较高的实用性,使得目标图像中可呈现亮度的线性转变,降低目标图像潜在亮度的敏感性,降低匹配块和目标块存在的变形差异,确保修复后的数字图像中不存在模糊区域和边界纹路,增强图像修复质量.