低液气密度比横向射流一次雾化模拟研究
杨 帆,叶桃红
(中国科学技术大学 热科学和能源工程系,安徽 合肥 230001)
横向射流雾化系统是传统燃气轮机燃烧装置的重要组成部分,在航空、航天、舰船、农业等方面具有广泛应用。一次雾化的机理研究起源于圆管射流雾化研究,Reitz[1]基于小扰动假设,提出了一次雾化和界面不稳定相关,并且最大增长速率的表面波决定了液滴的生成。但是这一理论仅适用于低速射流。在高速射流方面,Wu和Faeth[2]通过研究直射式喷嘴入注静止空气的雾化现象,提出了湍流诱导一次雾化机理,即湍流涡旋提供的能量与气动压降的能量之和大于生成的液滴所需要的表面能时,液滴将生成。Wu和Faeth 提出当液气密度比大于500时,空气动力学效应将被抑制,湍流成为驱动液滴形成的唯一机制。当密度比小于500,空气动力和湍流都是一次雾化的重要驱动力。Sallam[3]在横向射流实验中也发现了类似的现象,管内流动为湍流的横向射流的雾化同时受到湍流和空气动力学因素的影响。Arienti[4]在混合欧拉-拉格朗日框架下,采用VOF方法描述连续的液核与气相,采取拉格朗日粒子追踪一次雾化生成的液滴,结合湍流是液滴生成的重要驱动力,研究了常温常压下液气密度比为612和773的燃料的一次雾化,研究获得的液滴直径和液滴速度与实验结果基本吻合。在现代燃气轮机中,为了在短时间内实现高效的混合与燃烧,通常空气经过进气口压缩机压缩为高压空气喷注到燃烧室内[5],此时液体燃料和横流气体之间的密度比要比常温常压下的密度比低,此时一次雾化不仅受到湍流的影响还受到空气动力学影响。显然Arienti的研究没有考虑到空气动力学的影响,不能直接应用于实际燃气轮机工作工况下的雾化。本文在Arienti工作的基础上,对低液气密度比下的横向射流一次雾化进行了模型修正,并开展了数值仿真计算及分析。
1 数学物理模型
1.1 基本控制方程
设生成的液滴的体积分数为,那么连续相的相体积分数为。设连续相中液相的体积分数为α1,密度为ρ1,连续相使用VOF方法追踪连续相。
连续相的连续性方程为

(1)
式中:U为混合物速度,m/s;Sα为由一次雾化引起的连续相的质量损失,m/s。
质量交换的源项为
(2)
式中:Vcell为网格体积,m3;Δt时间对应网格因为雾化损失的质量为mp,kg。
连续相的动量方程为

-(1-ε)p+(1-ε)ρg+Mout+Mex+MS
(3)
式中:Reff为有效应力,包括黏性应力与雷诺应力的贡献,N/s;g为重力加速度,m/s2;Mout为一次雾化引起的连续相动量损失,N/s;Mex为连续相与液滴之间的动量交换,N/s;MS为连续相之间的表面张力,N/s;表面张力采用CSF模型[6]计算。
一次雾化仅引起液相的动量损失:
Mout=ρ1SαU
(4)
一次雾化生成的液滴采用拉格朗日粒子追踪,通过计算网格内液滴体积确定,液滴受到的曳力采用Schiller- Naumann模型[7],由于气体湍流引起的湍流分散力采用Shirolkar JS随机漫步模型[8],液滴的碰撞和聚合采用O’Rourke模型[9],由于实验中没有观测到明显的二次破碎现象,因此在后续计算中并没有采用二次破碎模型,此外由于蒸发的时间尺度远大于液滴在计算域中的停留时间尺度,因此液滴也没有采用蒸发模型。
1.2 一次雾化模型
在Arienti的研究基础上,将同时受到液体湍流和空气动力学因素影响的一次雾化拆分为两个过程:
(1)第一阶段仅仅受到液体湍流的作用,不受空气动力学的影响,完全由湍流诱导的一次雾化经历雷诺破碎[10],根据理论分析其液丝大小满足:
(5)
式中:τR为雷诺破碎的时间尺度,采用湍流涡旋到达离喷嘴距离为y的位置的时间尺度来估算,s;Uy为当地流速在射流方向的速度分量,m;C为经验参数,这里采用Sallam[3]实验中拟合的值0.4。
(2)第二阶段完全受空气动力学的影响,液丝破裂生成更多的小液滴,液滴直径和液丝直径之间的关系为[11]
(6)
式中:ρf为液相密度,kg/m3;ρg为气相密度,kg/m3;μf为液相黏度,Pa·s;li为液相长度尺度,m。
上述关系式仅仅适用于静止空气中的破碎,为了在横向射流中使用,引入气相和液丝的滑移速度Ur=Ul-Ug。Uinf采用当地的液相平均速度,Ug采用来流气相速度近似。
一次雾化产生的液滴的质量采用Arienti提出的计算方式:
mp=ηρlμpSΔt
(7)
式中:S为界面的面积,m2。采用isoadvector[12]的Iso-Surface算法估计界面面积,已经证明该方法为二阶精度。
不同于M. Arienti采用固定的雾化速率,这里采用Le[13]的实验表达式,把雾化速率和破碎点高度结合在一起,越靠近破碎点,雾化速率越高。
(8)
式中:yb为横向射流雾化破碎点高度,m。破碎点高度采用如式(9)估计:

(9)
式中:dj为喷嘴的直径,m;q为动量通量比;Cb为一个和喷嘴设计、管内流动状态相关的经验参数。对于长径比为10的喷嘴,Cb取为3.3[14]。
1.3 计算工况
数值模拟的几何体的结构如图1所示。图1中入射孔直径D=457 μm,喷嘴长度L/D=10,位于空气入口下游5 mm中心线上,空气入口宽度为46 mm,沿着射流方向的高度为30 mm,通道长度为74.6 mm。数值模拟的设置和Y.Gopala.E[15]的实验设置一致,研究液气密度比为312,马赫数为0.2和0.35的预热高压空气来流下,动量通量比为180时,液体燃料Jet A的雾化。具体的算例的主要参数见表1,Jet A密度为790,黏度为0.001 9,与空气之间的表面张力系数为0.022。
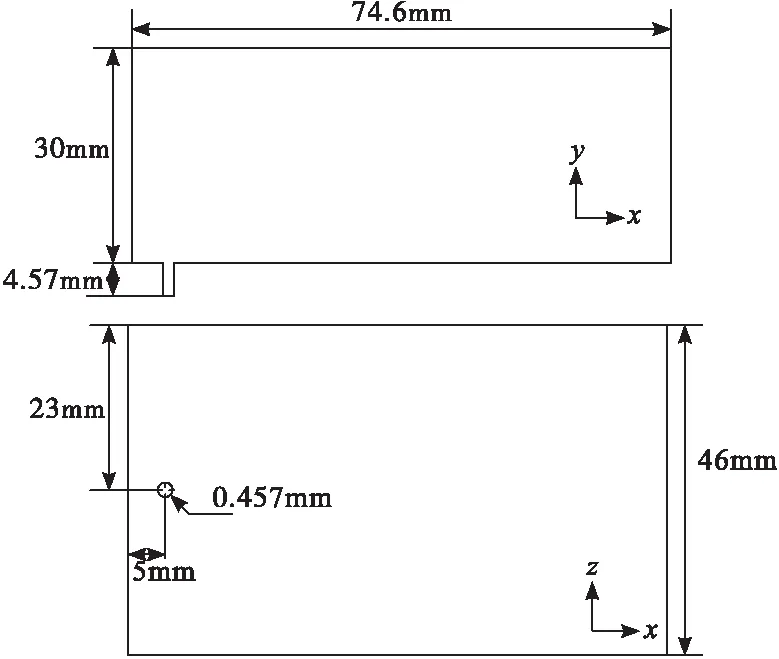
图1 计算域示意图

表1 LJIC算例设置
1.4 数值方法和边界条件
1)边界条件
根据实验测量在喷嘴上游5mm处的空气流场属于充分发展的湍流,且该位置的气体流动基本不受射流流动的影响,气体湍流强度为4%,根据幂次定律,空气入口的速度分布满足[4]:

δT>dw→u=uinf
(10)
式中:δT为速度边界层厚度,mm,依据实验测量,入射孔板上的边界层厚度约为3 mm;dw为入口平面内任意点到壁面的最短距离,mm;Uinf为主流区流速。液体入口给定平均速度。出口采用压力出口,假设出口各个物理量零梯度。壁面采用了无滑移壁面边界条件。
2)数值方法
计算采用的求解器基于OpenFoam-7开发,采用有限体积方法离散控制方程,相体积分数方程的对流项采用Gauss vanLeer格式,其余方程对流项采用bounded Gauss Gamma格式,扩散项采用中心差分格式,湍流模型采用k-omega SST VLES模型[16]。速度-压力修正采用PIMPLE算法。计算中控制最大库朗数为0.6,计算中所有线性方程组的归一化误差设为10-8。所有的拉格朗日粒子统计时采用如下策略:计算射流稳定后的3个时间步内的粒子在边长为1.5 mm的小正方体内的属性平均值。
1.5 网格无关性验证
为了排除网格对于计算结果的影响,采用了稀疏、中等、稠密的三套网格进行计算,网格的总数量分别为75万、143万、300万,网格在壁面和喷嘴附近进行了加密。三套网格在壁面和喷嘴附近的最小尺度分别为0.044D、0.021D和0.01D,D为喷嘴直径。
图2(a)为三种网格在平面z=0内相体积分alpha为0.5的界面等值线,从图中可以看到中等规模的网格下,计算得到的相界面和密网格下的结果差距不大,主要的差异处于破碎点附近,而稀疏网格计算的相界面的高度明显偏低。为了检查拉格朗日粒子统计值与网格大小的关系,统计了喷嘴下游20 mm附近一个长和宽为1.5 mm,沿着射流入射方向,高为30 mm的长方体内的液滴速度,图2(b)展示了不同网格下,在喷嘴下游20 mm处液滴速度的概率密度统计,可以看到稀疏网格下液滴速度分布概率密度最大值略低于中等网格和密网格计算所得的最大值,中等网格和密网格计算得到的液滴速度分布基本一致。结合上述讨论,在后面的计算中将采取中等网格进行计算。

图2 不同网格下的计算结果
2 计算结果与讨论
Elsam[17]和Yogish Gopala[18]通过实验测量了高温高压下的射流轨迹,图3为Case 1和Case 2模拟获得的射流轨迹和Elsa和Yogish Gopala获得的经验关系式对比图。模拟获得的Case 1和Case 2射流轨迹高度与上述经验公式相比都偏低,Case2更加明显。可能的原因是Elsam和Yogish Gopala的测量的动量通量比的最大值为40,模拟的Case的动量通量比为180,动量通量比代表了液体射流和气相横流的惯性力之比,对射流轨迹的影响很大。另外模拟的射流的边界条件与实验真实情况存在一定的偏差,也是造成射流轨迹偏低的重要原因。

图3 射流轨迹对比图

图4 Case 1和Case 2在y=0截面上的液滴速度分布
图4为Case1和Case 2 在y=0截面上的液滴速度分布图,液滴大小为实际大小的24倍,并采用液滴的速度大小着色,图中灰色部分为液柱,可以清晰地看到液滴从液柱背面剥离的表面雾化现象,且越远离壁面的液滴其直径越大,这可以通过液体湍流是驱动一次雾化的动力因素来解释,喷嘴出发到达更远的地方的湍流涡旋的时间尺度更大,相应的其长度尺度更大,而产生的液滴直径又和液体湍流涡旋的长度尺度成正比,因此离喷嘴越远的液滴的直径也就越大。大液滴主要集中于液柱破碎点后,但是最大液滴出现破碎点下游,这说明这些更大的液滴不是由于雾化破碎产生而是液滴聚合产生。另外Case2的液滴直径明显小于Case1的液滴直径,虽然Case1 和Case2有相同的动量通量比,但是Case2的液体入射雷诺数更大,液体湍流的长度尺度更小,在湍流驱动雾化假设下产生的液滴直径相对就较小,Case2的气体韦伯数相对于Case1的更大,这意味着Case1中空气动力学作用更强,在空气动力学作用下,将产生的更小的液滴。从液滴速度来看,靠近喷嘴所在的壁面的液滴的速度往往较小,而远离喷嘴所在壁面的液滴的速度较大。这是由于表面破碎产生的液滴和液柱背面的The Wake[29]区域进行动量交换,速度迅速和当地气流速度一致,在The Wake区域内保持较小的速度向下游运动,而远离喷嘴所在壁面的大液滴直接受到来流气流的影响,液滴和来流气流进行动量交换,液滴速度逐渐和来流速度相同,因此这些大液滴的速度更大。

图5 Case 1和Case 2在x=20 mm处的液滴D32、D10和液滴速度统计图
图5(a)和图5(b)给出了Case1和Case2在喷嘴下游20 mm处的液滴的D32和D10的统计信息与实验测量值的对比,液滴直径分布和图4中提及的现象一致,随着液滴远离壁面液滴直径逐渐增大,且Case 2产生的液滴直径比Case 1小。图5(c)给出了Case 1和Case 2在喷嘴下游20 mm处液滴速度大小的统计信息与实验测量值对比,为液滴速度,和实验数据一样仅考虑空气流动方向和射流入射方向的速度,为来流空气速度。可以看到液滴的速度大小和来流空气速度大小有明显的区别,其最大的特点为液滴的速度相对于气体来流速度有较大的滞后,Case1 和Case 2在喷嘴下游20 mm处液滴的速度大小的分布十分相似,Case 2的液滴的速度滞后率相对较小,最大滞后位置相对于Case 1偏后。这说明动量通量比对液滴的速度分布起决定性的影响。在y/D大于40后,模型预测的D32明显比实验值低,可能是由于射流穿透深度预测偏低引起。Case 2中液滴的速度最大滞后位置预测相对于实验值偏后,除了液滴直径在y/D大于30后与实验有一定差别外,液滴直径和液滴速度分布与实验基本一致。
3 结 论
本文在混合欧拉拉格朗日框架下,针对低液气密度比同时受到液体湍流和空气动力学影响的横向射流,引入了一次雾化的液滴直径的修正,发展了新的一次雾化模型。对液气密度比为312、空气入口马赫数为0.2和0.35以及液体射流和空气主流的动量通量比为180的直射式喷嘴的横向射流雾化开展了模拟,结果表明模拟射流轨迹与实验经验关系式相比偏低,除了液滴直径在y/D大于30后与实验有一定差别外,液滴直径和液滴速度分布与实验基本一致。
致谢
感谢中国科学技术大学超级计算中心对本文数值模拟计算的支持。

