图的最小度和无矛盾连通数
严政,赵小鹏,慈永鑫
长江大学信息与数学学院,湖北 荆州 434023
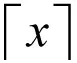

1 基本结果
关于图G的无矛盾染色,CZAP等[2]首先确定了路径的无矛盾连通数。
命题1[2]设Pn表示有n条边的路径,则:
设C(G)是G中由割边诱导的子图,用Q1,Q2,…,Ql表示C(G)的分支,记h(G)=max{cfc(Qi):Qi是C(G)中的分支}。
命题2[2]设G是一个有割边的连通图,则:
h(G)≤cfc(G)≤h(G)+1
对于阶为n的连通图G,1≤cfc(G)≤n-1;当且仅当G=Kn时,cfc(G)=1;当且仅当G=K1,n-1时,cfc(G)=n-1[3,5,10]。若G是非完全图,则cfc(G)≥2。特别地,对于2-连通图,cfc(G)=2;文献[3,11]进一步得到,对于非完全2-边连通图,cfc(G)=2。
命题3[2]设G是一个非完全2-连通图,则cfc(G)=2。
设t是正整数,G的t-冠(corona)是指向G的每个顶点添加t条悬挂边所构成的图。
命题4[2]设Cn=v1v2,…,vn(n≥4)是一个圈,G是它的2-冠,则cfc(G)=3。
命题5[2]设G是一个有割边的连通图,则cfc(G)≤max{2,|E(C(G))|}。
引理1[2]设G是一个连通图,则从G的每一个非平凡块中适当选择一条边,可形成G的一个匹配。
引理2[2]设G是一个2-连通图,e∈E(G),则G中任意2个不同的顶点u和v之间存在1条包含e的u-v路径。
关于无矛盾连通数的更多结论,详见文献[3]和[10,11]。
2 主要结果
2.1 阶小于ks+2s+3k+6(s≥k≥2)的连通图的无矛盾连通数
定理1设G是一个阶为n(n≥2)的连通图,其中n≤ks+2s+3k+5(s≥k≥2)。如果δ(G)≥s+2,则cfc(G)≤k。
证明先用反证法证明G至多有k条割边。假设G有l(l≥k+1)条割边,则删除G的所有割边得到l+1个连通分支,设H0是其中最小的分支。
情形1|V(H0)|=a≤s+2。
由于δ(G)≥s+2,所以H0中的每一个顶点都至少连接一条割边。设y为G中与H0关联的割边数,则:
整理得:
a(s+2)≤a(a-1)+y
即:
y≥a(s-a+3)
又:
a(s-a+3)-(s+2)=a(s+2+1-a)-(s+2)
=(s+2)(a-1)+a(1-a)
=(a-1)(s+2-a)≥0
因此,y≥s+2≥k+2。设G中与H0相关联的割边分别为e1,e2,…,ey,则G={e1,e2,…,ey}有y+1个连通分支,记为H0,H1,…,Hy。因为δ(G)≥s+2≥4,所以对于任意的Hi(1≤i≤y),都存在v∈V(Hi),使得N(v)⊆V(Hi),从而每个Hi至少有δ(G)+1个顶点。于是:
≥y(s+3)
≥(k+2)(s+3)
=ks+2s+3k+6
与n≤ks+2s+3k+5矛盾。
情形2|V(H0)|≥s+3。
由δ(G)≥s+2,得:
≥(l+1)(s+3)
≥(k+2)(s+3)
=ks+2s+3k+6
这与n≤ks+2s+3k+5矛盾。
因此G至多有k条割边。由命题5可知,当k≥2时,cfc(G)≤k。
定理1中的界是紧的。构造图Gk+1如下:记H0,H1,…,Hk+1均是阶为s+2的完全图,取H0中任意一点分别与H1,H2,…,Hk+1中的一点连接。此时,有:
|V(Gk+1)|=(k+2)(s+2)=ks+2s+2k+4
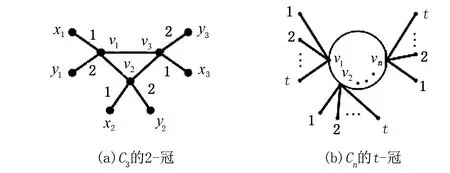
δ(G)=s+1 显然,cfc(Gk+1)=k+1。 特别地,当s=k时,得到下述推论。 推论1设G是一个阶为n(n≥2)的连通图,如果n≤k2+5k+5(k≥2)且δ(G)≥k+2,则cfc(G)≤k。 推论2设G是一个阶为n(n≥2)的非完全连通图,如果n≤5s+14(s≥2)且δ(G)≥s+2,则当G存在3条割边且相交于一点时,cfc(G)=3;否则cfc(G)=2。 证明由定理1可知,满足条件的G至多有i条割边,记为ei(i≤3)。 情形1G没有割边,即G由非平凡块构成。 根据引理1,从每一个非平凡块中选取一条边构成匹配M,此时令c(M)=1,c(E(G)-M)=2。 情形2G仅有1条割边。 从G中所有的非平凡块中选取一条边构成匹配M,令c(e1∪M)=1,c(E(G)-e1∪M)=2。 情形3G有2条割边。 删除2条割边有3个连通分支,分别记为H0,H1,H2。 1)如果e1和e2相邻,则令c(e1)=1,c(e2)=2。 2)如果e1和e2不相邻,则令c(e1)=c(e2)=2。 现在对每个连通分支进行染色,从每个Hi(0≤i≤2)中的非平凡块中取一条边构成匹配M,此时令c(M)=1,c(E(G)-{e1,e2}∪M)=2。 情形4G有3条割边且不相交于同一点。 删除3条割边有4个连通分支,分别记为H0,H1,H2,H3。 1)如果ei(1≤i≤3)各不相邻,即割边之间没有交点,此时令c(e1)=c(e2)=c(e3)=1。 2)如果ei(1≤i≤3)中恰有2条割边相邻,不失一般性,假设e1与e2相邻,此时e3和e1,e2均没有交点,则令c(e1)=c(e3)=1,c(e2)=2。 3)如果e1和e2相邻,e2和e3相邻并且e1和e3不相邻,则令c(e1)=c(e3)=1,c(e2)=2。 接下来从每个Hi(0≤i≤3)中的非平凡块中取一条边构成匹配M,令c(M)=2,c(E(G)-{e1,e2,e3}∪M)=1。 根据引理2可以验证,上述情形1~4中任意2个顶点之间都存在一条只需要2种颜色的无矛盾连通路径,即cfc(G)≤2,显然cfc(G)≥2,从而cfc(G)=2。 情形5G有3条割边且相交于一点。 由于任意2条割边之间都仅存在1条路径,因此3条割边的颜色互不相同。即cfc(G)≥3。另一方面,由定理1可知,cfc(G)≤3。于是cfc(G)=3。 综合上述所有情形,推论2成立。 推论3设G是一个阶为n(n≥2)的非完全连通图,如果n≤4s+11(s≥2)且δ(G)≥s+2,则cfc(G)=2。 证明由定理1可知,满足条件的G至多存在2条割边,一方面,由推论2中情形1~情形3知,存在1种只需要2种颜色的无矛盾连通染色,于是cfc(G)≤2。另一方面,对于任意的非完全连通图,有cfc(G)≥2,从而cfc(G)=2。 引理3设G是一个由任意2-连通图中每个顶点都悬挂t条边所构成的图,则: t≤cfc(G)≤t+1 证明对于有割边的连通图G,由于每个顶点悬挂t条边,因此h(G)=t。根据命题2,有: t≤cfc(G)≤t+1 对一种特殊的2-连通图Cn,文献[2]研究了Cn(n≥4)的2-冠,得到其无矛盾连通数为3。下面给出Cn(n≥3)的t-冠(t≥2)的无矛盾连通数。 定理2设Cn=v1,v2,…,vn(n≥3)是一个圈,G是它的t-冠,其中t≥2,则: 证明由于G是Cn中每个顶点通过添加t条悬挂边得到的图,即h(G)=t。由引理3,有cfc(G)≥t。下面分2种情形讨论。 情形1t=2。 1)如果n≥4,则由命题4可知,cfc(G)=3。 2)如果n=3,此时假设cfc(G)=2。如图1(a)所示,与顶点vi(1≤i≤3)相连的2个悬挂点分别记为xi,yi。因为与vi相连的悬挂边之间仅有1条路径,所以需染不同的颜色,令c(vixi)=1,c(viyi)=2(1≤i≤3)。对于C3,由命题3可知,2-连通图的无矛盾连通数为2。因此根据对称性,不妨令c(v1v2)=1,c(v1v3)=c(v2v3)=2。由引理2可知,对C3中任意2个顶点之间的路径均选择通过染颜色1的边。这时任意选择x1-x2之间的路径,都无法找到一条无矛盾连通路径。与假设矛盾。因此cfc(G)≥3。另一方面,由引理3知,cfc(G)≤3,故cfc(G)=3。 图1 圈的悬挂边Fig.1 Pendant edges of cycle 情形2t≥3。 由上述易知,只需证明cfc(G)≤t。如图1(b)所示,定义染色规则如下:不失一般性,在Cn中选择任意2条边并给它们染颜色1和2,Cn中所有剩余的边都染颜色3,与每个vi相邻的K1,t分别用1,2,…,t进行染色。此时,上述染色方式使得G中任意,2个顶点之间都存在一条无矛盾连通路径,于是cfc(G)≤t。证毕。 命题6[5]设G是一个阶为n(n≥2)的连通图,k(k≥2)为整数。如果: 则: cfc(G)≤k 命题7[6]设G是一个阶为n(n≥2)且包含割边的连通图,k(k≥2)为整数。如果: 则: cfc(G)≤k或 Δ(C(G))≤k+1 引理4[12]设G是一个具有t条割边且最小度为δ=δ(G)的n阶连通图,则: 其中: 定理3设G是一个阶为n(n≥2)的连通图,k(k≥2)为整数,如果: 则: cfc(G)≤k 其中: 证明用反证法。假设cfc(G)≥k+1,由命题5知,|E(C(G))|≥k+1,根据引理4,有: 特别地,当δ(G)≥k+2时,m=0。于是有下述推论。 推论4设G是一个阶为n(n≥2)且δ(G)≥k+2(k≥2)的连通图,如果: 则: cfc(G)≤k 在已有无矛盾染色理论基础之上,利用图的最小度研究无矛盾连通数不超过k的图类,同时给出一些无矛盾连通数为2和3的最小度条件。此外,能否根据最大度或添加最大度条件去讨论图的无矛盾染色,在后续研究中可以尝试。目前只针对特殊图类进行了研究,如何确定任意给定连通图的无矛盾染色需要进一步的研究。2.2 Cn(n≥3)的t-冠(t≥2)的无矛盾连通数
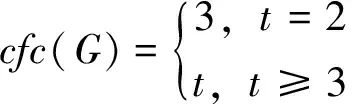
2.3 阶为n最小度为δ的连通图G的无矛盾连通数
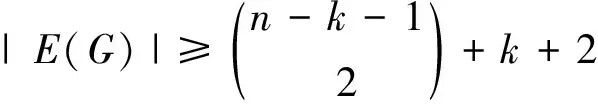



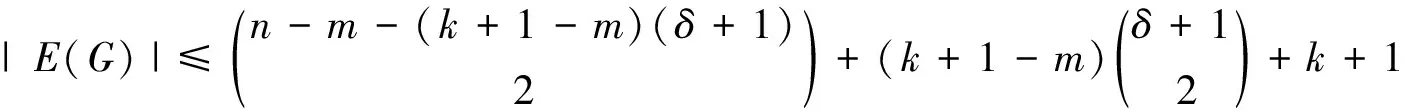

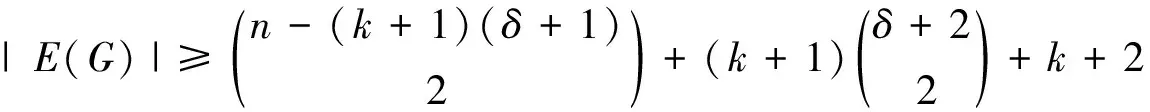
3 结语

