竖向外载作用下夹层海底管道凹陷行为研究

管锋，邓一波，张良振，万锋，刘先明，刘少胡

1.长江大学机械工程学院，湖北 荆州 434023 2.中国石化石油机械股份有限公司，湖北 武汉 430205

随着石油工业向深水领域发展，海洋油气资源安全输送对海底管道的结构承载能力和保温性能提出了更高的要求。近年来，出于经济性、安装和结构抗力等方面的考虑，填充聚合物或水泥基芯的夹层管被提出并用于深水环境[1]。

外压承载能力、弯曲特性、整体屈曲、管道连接方法和凹陷行为等是深水管道设计和安全评价中需要考虑的关键因素。针对夹层管，FU等[2]采用数值模拟方法对填充水泥基复合材料夹层管在外压作用下的屈曲和安装过程中的弯曲性能进行了研究，发现增加初始凹陷会降低夹层管的压溃压力，层间粘结性能和核心层厚度是影响管道结构行为的重要因素；HE等[3]对填充实体聚丙烯夹层管的后屈曲响应研究表明，增大内外管厚径比能提升夹层管的压溃压力，并且其影响程度还取决于其他结构参数和层间粘结条件；GONG等[4]发现良好的层间粘结性能能显著提高夹层管的屈曲传播压力和能量耗散能力；CHENG等[5]通过试验研究了夹层管的真实层间粘结特性，研究表明，夹层管的层间粘结能力较弱，与数值模拟中的层间无粘结情形接近，增大层间摩擦系数有利于提升管道的极限弯曲强度；CASTIHO和PASQUALINO[6]通过试验和数值模拟验证了机械损伤将导致夹层管抗压强度降低；ZHAO等[7]针对夹层管的热屈曲问题，利用变刚度梁扰度曲线Green函数法，求解建立了夹层管隆起屈曲临界轴向力计算公式；ONYEGIRI等[8]采用有限元法研究了夹层管用安装接头的弯曲力学行为，分析了内管壁厚、缩进长度、安装接头填料的刚度等对接头处应力集中的影响；QUISPE等[9]通过非线性有限元数值模拟对夹层管螺纹连接器进行分析，探究其在上扣扭矩、外部压力和轴向载荷下的接触应力和最大张力，结果表明，螺纹连接器是一种可行的夹层管接头解决方案。

现有研究主要针对夹层管的承压、弯曲、整体屈曲和管段连接方法等，包括含凹陷夹层管的承压能力，然而鲜有直接针对夹层管凹陷行为的研究。但在使用过程中，管道遭受第三方载荷而出现凹陷损伤时，必须进行凹陷评价，这需要对夹层管的凹陷力学行为进行深入理解。QIAN等[10]对夹层管在准静态垂直载荷下的结构凹陷行为进行了实验和数值研究，获得了其载荷与凹陷深度关系。但研究并未考虑内外部压力效应，同时管道两端处于自由边界条件，与实际海底管道约束条件存在一定差异。除此之外，单层管凹陷行为研究的方法和手段可以作为夹层管研究的基础。WIERZBICKI和SUH[11]通过理论分析研究了楔形物体加载下管道的凹陷行为，并提出了不同约束条件下凹陷深度预测模型；KARAMANOS和ANDREADAKIS[12]考虑内压的影响，建立了管道凹陷深度计算模型，并且研究发现内压的存在显著提升了管道抵抗凹陷的能力；同时，DNV规范[13]推荐了海底管道撞击损伤风险评估及凹陷深度预测方法。

总体而言，对夹层海底管道在深水环境下的工程应用，现有凹陷力学行为研究未考虑内外部压力的影响，且缺乏系统性研究，现有单层管凹陷深度理论预测模型和评价方法并不直接适用于夹层管。因此，研究内外部压力作用下夹层海底管道的凹陷行为，对夹层管设计及安全运行具有重要意义。为此，笔者对现有海底管道的凹陷深度和应变计算方法进行了梳理，在此基础上建立了夹层管凹陷变形有限元模型，研究了其载荷位移关系和应变特征等凹陷力学行为，探究了核心层厚度和强度、内部介质压力和落物尖锐程度等因素对夹层管凹陷承载能力和凹陷应变的影响。

1 凹陷深度预测模型及应变计算方法

工程中对凹陷管道的评价有2种方法，即基于深度的评价方法和基于应变的评价方法[10]。基于深度的评价方法规定凹陷深度不大于6%的名义管径，基于应变的评价方法规定凹陷区应变不大于6%，否则管道需要移除或修复。研究凹陷深度与外载荷的关系有利于提升管道的耐撞性设计，并能为凹陷管道的检测维护提供依据，对凹陷区域应变的研究则能为凹陷管道提供更精确的评价。

1.1 凹陷深度与外载荷关系

对单层管而言，外载荷与凹陷深度的关系可通过塑性力学方法建立。刚性基础上两端固定约束管道的外载荷与凹陷深度关系式的推导，建立在刚-塑性三维圆柱壳模型基础之上[11]。该模型由一系列非连接的横向圆环和纵向弦线(梁)构成，如图1所示。横截面圆环为包含4个可移动塑性铰的刚-塑性环模型，并假定其周向不可扩展。纵向弦线被视为随凹陷深度变化发生弯曲和拉伸(压缩)的刚-塑性梁模型，模型忽略了剪切变形和扭转变形，其破坏机制如图2所示。根据虚速度原理可建立凹陷深度与外载荷之间的关系式：

(1)

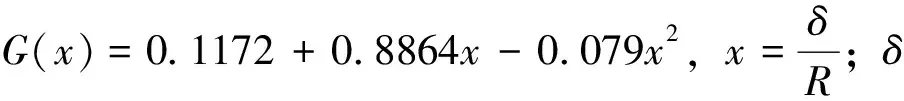
图1 刚塑性壳模型 图2 凹陷区域变形模式Fig.1 Rigid-plastic shell model Fig.2 Geometry deformation mode of denting zone

1.2 凹陷应变计算方法

凹陷区域管壁的凹陷应变包括环向弯曲应变εxb、轴向弯曲应变εyb和轴向薄膜应变εym，其表达式为[14]：

(2)

(3)

(4)

式中：Ri为管道内径，mm；R1为凹陷环向曲线的曲率半径，mm；R2为凹陷轴向曲线的曲率半径，mm；L为凹陷长度，mm。

对凹陷进行评价时，采用管道内外表面有效应变的最大值与允许的极限应变进行比较。管道内外表面的有效应变由塑性力学可计算得到：

(5)

(6)

由于材料硬化和夹层管复合结构特征，单层管凹陷深度与外载关系模型并不能直接应用于夹层管。理论公式不能准确反映夹层管道内管和外管凹陷区域的应变情况，而通过试验很难模拟内外压同时存在下夹层管的凹陷变形。因此，利用数值模拟方法研究夹层管凹陷力学行为较为简便，且非常有效。

2 夹层管凹陷变形数值模拟

2.1 有限元模型建立及验证

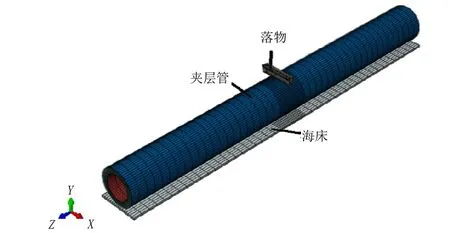
图3 坠落物体载荷作用下夹层管有限元模型Fig.3 Finite element model of sandwich pipe under dropped object load

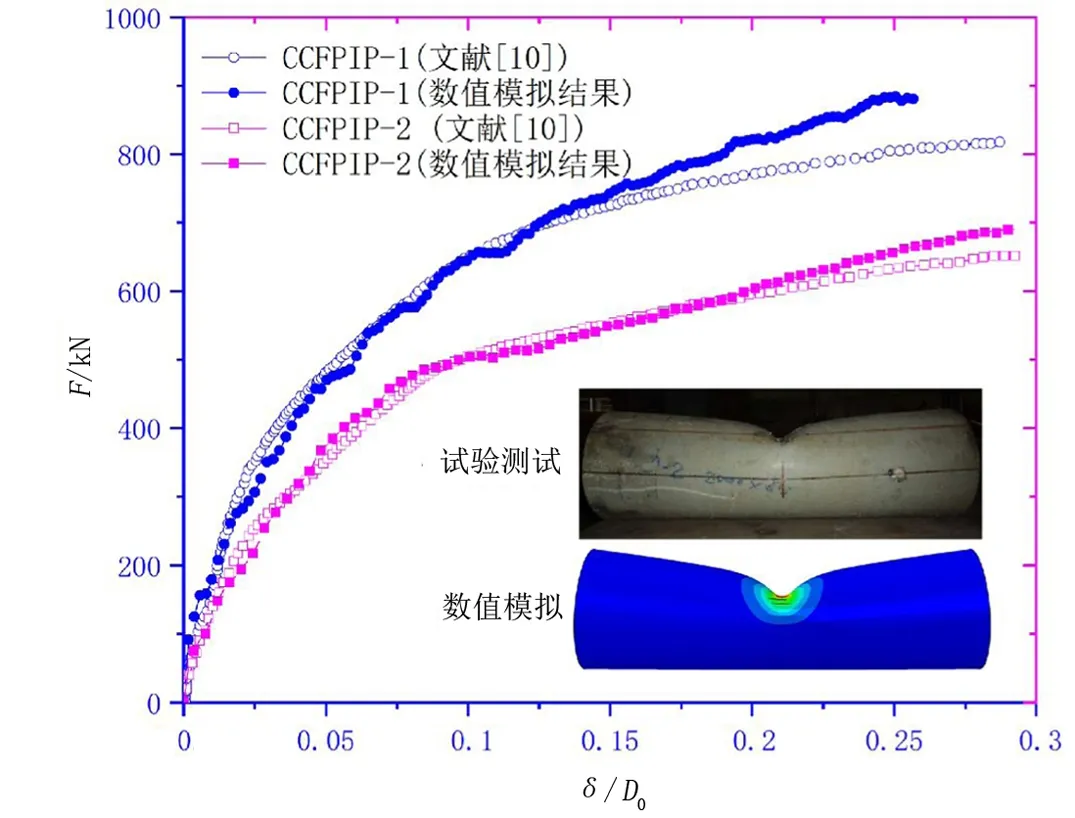
注：D0为外管直径,下同。图4 仿真结果与试验结果对比Fig.4 Comparison of simulation and test results

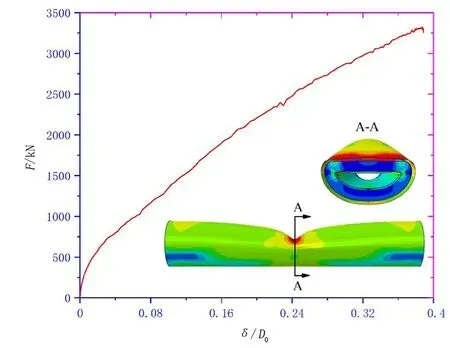
图5 夹层管外载荷-凹陷深度关系及失效模式Fig.5 The external load-denting depth relationship and failure mode of sandwich pipe

数值计算模型包括夹层管、坠落物体(落物)和海床3部分，如图3所示。落物形状为DNV规范中推荐的楔形落物轮廓[13]，考虑刚性海床的情形，撞击过程中落物的变形很小，忽略不计，故有限元建模中将海床和落物视为刚性体。

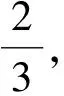
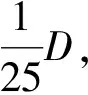
2.2 夹层管凹陷力学行为

以内部输送压力为10MPa,水深500m处的夹层管为研究对象。在内外部压力及落物外载联合作用下，夹层管在加载点处产生沿轴向两侧对称的向下单侧局部凹陷，如图5所示。凹陷中心截面形状由上部直线部分和两侧的缘弧部分构成，截面整体变形与薄壁管类似，符合塑性铰变形机制，如图2所示[11]。图5同时展示了凹陷深度与落物外载的关系曲线，结果表明，落物外载随着凹陷深度的增加非线性加载，即在外载荷作用下夹层管凹陷变形呈现出非线性平衡路径；在凹陷初期材料处于弹性范围内，载荷-位移曲线呈线性变化，但该过程极短；随着凹陷深度增加，管道逐渐出现塑性变形，管道刚度发生变化，载荷-位移曲线表现出非线性变化特征；当凹陷深度继续增加，由于材料硬化和薄膜应力效应，夹层管的凹陷承载能力得到强化，结构抗力随凹陷深度近似线性增长。

对凹陷夹层管内外管的应变分布进行分析，如图6所示。整体而言，内外管环向应变和轴向应变均沿凹陷中心往管道远端逐渐变小，管道水平横截面上下两侧应变分布不对称。具体地，外管的环向压缩应变发生在凹陷中心截面两侧(塑性铰区域)，外管其他区域均处于环向拉伸应变状态，且凹陷中心附近顶部和底部的应变更大，环向压应变水平要远高于拉应变水平；外管整体处于轴向拉应变状态，凹陷中心应变状态明显高于其他区域，凹陷区域两侧局部区域产生了少量的轴向压缩应变，这是由落物压缩挤压造成的。与环向应变不同，凹陷区域轴向高应变区域存在与管道顶部。

内管的应变分布与外管有所不同，由于水泥基复合材料的约束作用，在凹陷过程中内管整体基本处于环向压应变状态，只有凹陷中心附近区域发生少量的环向拉伸应变；内管轴向应变拉伸区和压缩区的分布规律与外管一致，但内管顶部和底部应变与两侧应变的分化相比外管要更为显著。

图6 夹层管应变分布Fig.6 The strain distribution of sandwich pipe

图7对比了内外管凹陷中心截面关键点处的环向应变和轴向应变，可以发现，截面顶点环向和轴向的应变值均要大于截面侧面点对应的应变值；相同位置，内管环向的应变值要大于外管，而外管的轴向应变值要高于内管。这体现出夹层管凹陷过程中外管承受更大的轴向拉伸载荷，而由于复合结构的约束效应，内管的环向受力更大。

图7 内外管凹陷中心截面应变对比Fig.7 The comparison of strain in the central cross-section of inner and outer tube indentation

3 凹陷应变影响因素分析

3.1 凹陷承载能力参数敏感性分析

分别考察了核心层厚度、核心层抗压强度、内部介质压力和落物底部的尖锐程度等4个因素对夹层管凹陷承载能力的影响。凹陷承载能力通过凹陷深度与外载特征曲线进行表征，核心层厚度通过引入环空率来表示，环空率越大则核心层厚度越小。核心层抗压强度指填充的水泥基复合材料的抗压强度，落物底部尖锐程度指落物底部半圆轮廓直径的大小。

图8分别展示了核心层厚度、核心层强度、内部介质压力和落物底部半径对夹层管凹陷承载能力的影响。可以看出，核心层厚度、核心层材料强度和内部介质压力均为夹层管凹陷承载能力的重要影响因素，而落物底部尖锐程度对凹陷载荷承载能力影响不明显；减小环空率、提高核心层抗压强度以及增加内部介质压力对夹层管的凹陷承载能力有不同程度的增强效果，其中核心层厚度的增强效果最明显。随着环空率降低，夹层管的刚度和结构强度显著提升，且随着凹陷深度的增加，环空率降低带来的增益效果越来越明显，如图8(a)所示。图8(b)比较了30、50和70MPa等3种不同核心层抗压强度下夹层管的载荷-凹陷深度关系曲线。在凹陷初期3条曲线基本重合，重合段相对不同环空率下的情形(如图8(a))明显变长；当核心层强度由30MPa增加到70MPa时，不同凹陷深度下夹层管凹陷承载能力约提升20%左右。内部介质压力由4MPa提升至10MPa时，夹层管刚度有一定程度的提升，凹陷深度越大压力增强效应越明显，如图8(c)所示。当凹陷深度不超过1%外管外径时，内部压力对载荷-位移曲线基本无影响；落物底部半径对夹层管凹陷承载能力的影响如图8(d)所示，底部半径为15、35mm的落物对应的载荷位移曲线重合；当凹陷深度超过6%外管外径后，底部半径为5mm的落物其对应的载荷位移曲线比15、35mm情形下的载荷位移曲线稍低，说明在较大凹陷深度下，尖锐的落物底部轮廓会在一定程度上降低夹层管凹陷承载能力；此外，观察凹陷区域的变形模式可知，落物底部半径越尖锐，凹陷轮廓曲率越大。

图8 不同参数对凹陷承载能力的影响Fig.8 The influence of different parameters on the indentation bearing capacity

需要注意的是，环空率的增加必然引起管道整体质量的增加，从管道安装和经济性角度出发，需要寻求一种折中的方案。而内压的增益效果实际上与夹层管的整体厚度有关，不同厚度下，内压的增益效果不同。

3.2 管道等效塑性应变与设计参数关系

应变是凹陷管道的评价指标之一，分析夹层管凹陷应变对其凹陷评价具有重要意义。为此，分别考察了核心层厚度、核心层强度、内部介质压力和落物底部轮廓等参数对内外管等效应变的影响，结果如图9所示。分析结果表明，4种单一因素影响下外管等效塑性应变水平均高于内管，内管等效塑性应变只有外管等效塑性应变的1/3左右。

图9(a)为0.5、0.7和0.9等3种环空率下外管和内管的等效塑性应变，等效塑性应变与凹陷深度的关系曲线呈“S”型，随着凹陷深度的增加等效塑性应变逐渐变大；随着环空率增大，外管和内管的等效塑性应变均呈减小趋势；当凹陷深度为15%外管外径时，环空率由0.5增大到0.9使得外管和内管的等效塑性应变分别减低25%和42%，这是由于核心层厚度减小降低了夹层管的刚度，产生相同深度的凹陷所需的外载荷也随之降低，从而导致内外管产生的等效塑性应变也相应变小。

核心层强度对内外管等效塑性应变的影响如图9(b)所示，等效塑性应变随凹陷深度增加呈“S”型增长。凹陷深度为15%外管外径时，30、50和70MPa等3种不同核心层抗压强度对应的外管等效塑性应变分别为0.39、0.40和0.41，对应的内管等效塑性应变分别为0.13、0.11和0.14，结果表明核心层强度提高对内外管等效塑性应变的影响基本可以忽略。

内部介质压力对内外管等效塑性应变的影响与核心层强度类似，如图9(c)所示，在最大凹陷深度处，4、6和10MPa 3种内压对应的外管等效塑性应变分别为0.381、0.389和0.396，对应的的内管等效塑性应变分别为0.135、0.132和0.13，内外管等效塑性应变的变化幅度小于4%，因此可认为内部压力对等效塑性应变基本无影响。

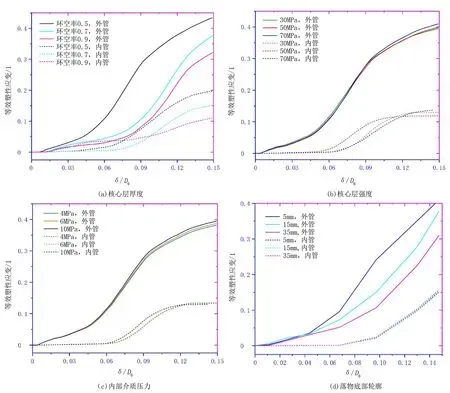
图9 内外管等效塑性应变随设计参数的变化Fig.9 The variation of equivalent strain of inner and outer tubes with design parameters

落物底部尖锐程度对等效塑性应变的影响如图9(d)所示，内外管等效塑性应变与凹陷深度近似呈抛物线关系，随着凹陷深度的增加等效塑性应变快速增长；随着落物底部半径增大，外管等效塑性应变降低，内管等效塑性应变升高；最大凹陷深度处，5、15和35mm落物底部圆弧半径对应的外管等效塑性应变分别为0.398、0.358和0.297，降幅为25%；对应的内管等效塑性应变分别为0.15、0.152和0.156，增幅为4%。由此可知，落物底部半径对外管的等效塑性应变影响非常显著，对内管等效塑性应变的影响可忽略不计。落物底部越尖锐，外管产生的等效塑性应变越大。

4 结论

1)内外部压力与外载荷联合作用下，夹层管的凹陷变形平衡路径表现为非线性特征。外载造成夹层管单层局部凹陷模式，凹陷中心横截面截面变形符合塑性铰变形机制。

2)凹陷夹层管外管的塑性应变远高于内管，核心层厚度减小有利于降低内外管的最大等效塑性应变。外管的轴向拉应力要大于内管，由于夹层结构的约束效应，内管的环向应变值要高于外管。

3)核心层厚度、强度和内部压力有益于提升夹层管结构抗力，其中核心层厚度增益效果最佳，但同时也要从安装和经济性角度出发综合权衡。落物底部尖锐程度对夹层管的凹陷承载能力影响有限，但尖锐的底部轮廓会使外管塑性应变显著增加。