基于IMM-PPO的无人机机动目标追踪

成旭明，丛玉华，欧阳权，王志胜

(南京航空航天大学自动化学院，南京 210016)

0 引言

随着航空、军事领域的发展，空中侦察追逃、灾后搜索救援等任务的危险和损耗与日俱增。无人机因其高机动性、低成本性，在这些任务中得到广泛的应用[1-2]。如何使无人机在复杂环境下具备自主避障导航与跟踪机动目标的能力是在实际应用中需要解决的难题，为此国内外学者进行了深入研究。

智能体在复杂环境中进行自主避障跟踪可以视为一类具有动态目标点的路径规划问题，在常见的路径规划问题上，Duchoň等[3]通过生成详细网格地图为智能体提供全局信息，采用改进的A*算法完成路径规划。Huang等[4]采用RRT算法在环境不确定性下规划智能体轨迹。Li等[5]将规划问题转换为目标优化问题，并提出了一种基于牛顿引力的启发式算法进行搜索寻优。上述的路径规划策略在全局规划上具备一定的优势，但对智能体模型与地图环境的信息有较高的要求。

随着计算机技术与人工智能的发展，一些研究者尝试将强化学习应用于无人机导航任务中，取得了不错的成果。Q-learning是强化学习中一种较为常用的算法，能够通过判断长期折扣奖励评估智能体的学习优劣[6]。Zhao等[7]设计了基于Q-learning的自适应路径探索与避障策略，用以无人机导航。Chao等[8]改进了Q-learning的动作选择策略并采用新的Q值初始化方法，使无人机具有更强的探索最优路径的能力。深度神经网络以其强大的函数逼近拟合能力，与强化学习结合衍生出许多改进算法，Jiang等[9]将经验回放思想引入DQN提出了MP-Dueling DQN，相比DQN在无人机避障与跟踪任务上具有更快的收敛速度与更强的泛化性。Guo等[10]采用分布式深度强化学习框架，利用LSTM神经网络处理时序问题的能力，提出了分层RQN的学习方法，能够在高动态环境中完成导航。以上方法虽然具备完成导航任务的能力，但也存在智能体动作空间离散的局限性。与这些方法中的离散动作空间不同，在实际应用中，无人机的动作空间往往是连续的，在现有的研究中，Li等[11-12]基于连续动作空间的DDPG算法框架，改进了演员-评价者(Actor-Critic)网络结构，使其对历史观测具备更好的拟合能力，对地面目标跟踪性能更优。在DDPG探索中引入混合噪声，对飞行任务解构并基于迁移学习的思想进行预训练权重，在面对不确定环境时具有良好的泛化性。以上研究通过强化学习训练决策网络，能够对移动目标进行有效避障跟踪，但在面对具有混合运动模型的机动目标时，缺少了对目标的状态估计步骤，在实际任务中具有较大的偏差。

针对上述缺陷，提出一种基于交互式多模型滤波(IMM)和近端策略优化(PPO)的机动目标追踪跟随策略，定义了以无人机运动模型为基础的动作空间以及用来表示环境信息的状态空间，根据追踪时间、跟踪性能以及避障约束构建奖惩函数，设计避障跟踪决策网络并进行训练。根据仿真实验分析，提出的方法相比传统算法在动态环境中具备更优秀的追踪避障及跟踪性能。

1 问题描述

1.1 无人机运动模型

研究无人机在三维空间中的动态目标追踪任务，假设能够通过自动驾驶仪使无人机运动在某一固定高度，无人机在二维坐标系中满足如下的连续运动方程：

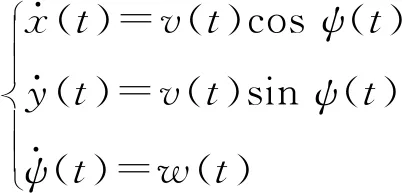
(1)

式中：x(t),y(t)为t时刻无人机在二维坐标系中的位置；v(t)表示t时刻无人机朝向方向的线速度；ψ(t),w(t)分别为t时刻无人机的偏航角与偏航角速度。将运动方程离散化可以得到从t时刻到(t+1)时刻的无人机状态更新方程为：

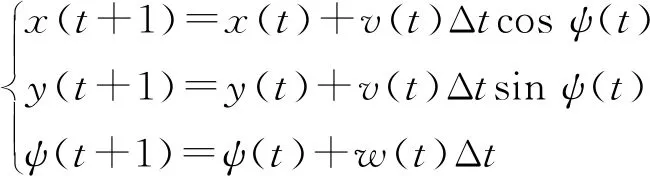
(2)

式中Δt为离散时间间隔。

1.2 任务目标及约束

无人机在复杂障碍物环境中追踪并跟随移动目标需要综合考虑目标跟踪性能与追踪耗时，同时需要满足任务过程中的避障约束。

1.2.1 目标跟踪性能

对机动目标的跟踪性能通常可以用无人机与目标的距离表示，提升跟踪性能即缩短无人机在单位时间内与目标的距离。跟踪性能对应的目标函数可以表示为：

(3)

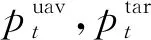
1.2.2 追踪耗时

在无人机实际执行目标跟踪任务时，会存在起始位置与目标起始位置相距较大的问题。在这种情况下，无人机需要自主规划路径以快速追踪并逼近机动目标，因此缩短无人机追踪目标的时间是需要考虑的另一个重要目标。追踪时间的待优化目标函数可以表示为：

minJ2=NΔt

(4)

式中N为无人机到达目标跟踪范围内的采样步数。

1.2.3 避障约束

在无人机的飞行域内存在大小、方位均未知的静止障碍物，可视为移动障碍物的敌方无人机，追踪无人机在感知到敌方无人机后能够获取其最大半径及当前时刻的状态信息。在复杂障碍物环境下，考虑到算法学习的收敛性，将实际观测窗信息进行处理，压缩至9条激光束，且每个激光束的相隔角度为22.5°，如图1所示。

图1 基于激光测距的无人机障碍物检测

图中:vuav为无人机当前的速度矢量;{di|d1,d2,…,dn}为第i个从无人机出发的激光束测得的与障碍物的距离，且di≤dmax。任务环境中存在静止障碍与运动状态已知的移动障碍，若在无人机导航过程中发生碰撞，则任务失败，因此无人机需要与障碍物保持合理安全的距离，约束条件为：

min(d1,d2,…,dn)>rsafe

(5)

式中rsafe为安全避障距离。

2 基于IMM-PPO的无人机避障跟踪

为了实现复杂环境下对机动目标更准确的跟踪，将IMM与PPO算法结合，对机动目标进行多模型融合状态估计，并将融合输出结合其他观测量构建状态空间，作为强化学习算法Actor-Critic网络的输入，训练无人机自主跟踪决策模型。作为一种基于策略的算法，PPO算法解决了传统策略梯度算法收敛依赖步长选择的问题并提高了经验利用率，使训练过程能够更快收敛。

2.1 跟踪目标状态估计

卡尔曼滤波常用于运动目标的状态估计，而在复杂环境下，机动目标的运动模型往往不是单一的，基于IMM的滤波方法能够考虑多个运动模型的转移概率，通过马尔可夫转移矩阵完成模型概率更新，从而得到多个滤波器的融合输出估计。IMM的优化过程如图2所示。

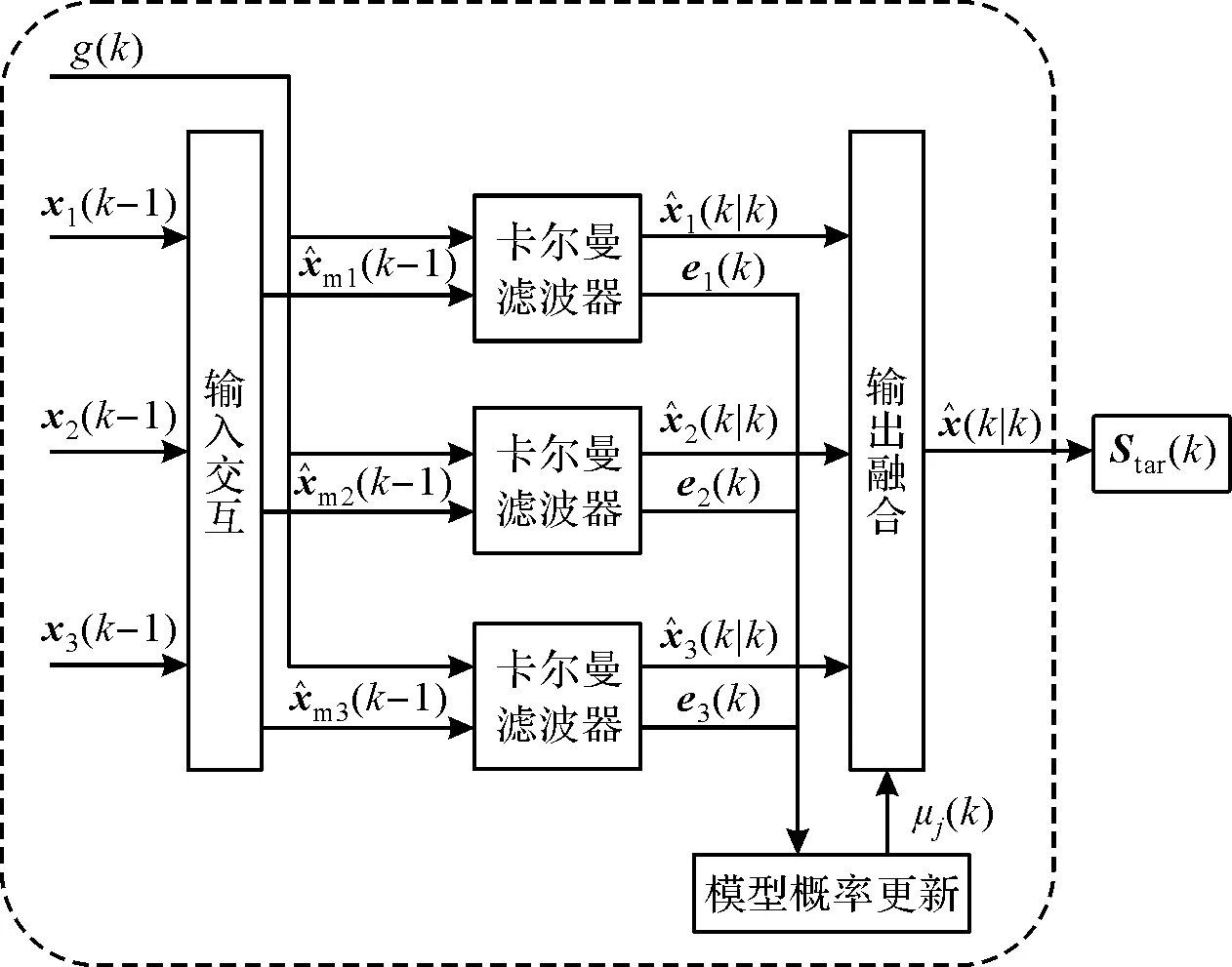
图2 交互式多模型滤波融合估计

定义模型间的概率转移矩阵P为:

(6)

其中pij(i=1,2,…,n;j=1,2,…,n)代表由模型i转换到模型j的概率，根据转移概率及概率更新计算模型混合概率为：

(7)

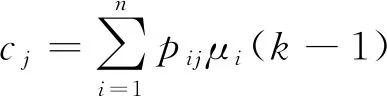
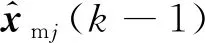
(8)

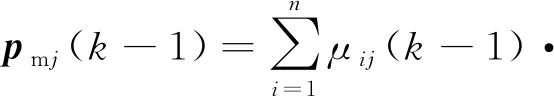
(9)

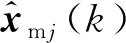
模型j的概率更新采用最大似然函数法，选取似然函数为：

(10)

式中vj(k),Sj(k)分别为滤波残差与其协方差，由对应于模型j的滤波器输出得到，概率更新方式为：

(11)

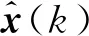
(12)

至此完成了k时刻运动目标的状态估计。

2.2 基于强化学习的目标跟踪框架

2.2.1 动作空间和状态空间设计

参照1.1节中无人机运动模型，以无人机朝向方向的线速度v与偏航角速度w作为控制量输入，强化学习动作空间可表示为：

A=(v,w)

(13)

状态空间从3个角度构建：1)无人机自身信息；2)对障碍物和动态威胁的观测量；3)机动目标的状态估计。在强化学习算法中，为了消除状态信息的维度不同对训练效果造成的影响，对状态空间St=(Sb,So,Star)中不同量纲的分量进行归一化处理，分别表示为：

(14)

(15)

(16)

其中：(xuav,yuav)为当前时间步下无人机于坐标系下的位置坐标；xmax,ymax分别为矩形飞行域的长、宽；ψ为无人机偏航角；vmax为无人机最大允许线速度；Svo表示碰撞域的状态信息；θ表示当前无人机和目标的连线与坐标系x轴所成夹角。无人机追踪机动目标的过程如图3所示。

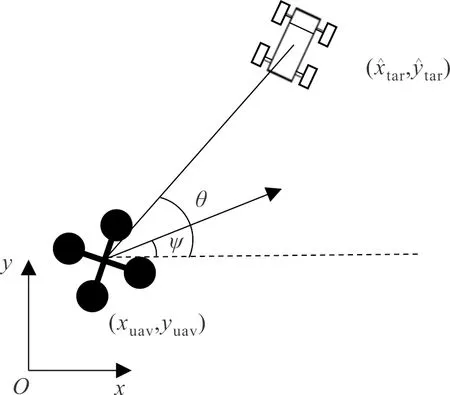
图3 无人机追踪机动目标示意图

2.2.2 奖惩函数设计

针对无人机自主避障跟踪的奖惩函数设计建立在指标函数与约束条件的基础之上。一种常用的设计思路是采用稀疏奖惩，即智能体仅在回合结束的情况下得到奖惩，这就需要智能体以不加引导的随机动作不断探索环境以获得奖惩，会导致算法的收敛速度降低，并且容易陷入局部最优解。因此在任务中，奖惩函数由稀疏奖惩与单步奖惩组成，稀疏奖惩仅在特定任务完成或回合结束时产生，单步奖惩则在智能体与环境的每一步交互后产生，旨在引导智能体更快地完成追踪任务。

1)障碍物惩罚函数

根据状态空间及避障约束条件设计障碍物惩罚函数，利用状态信息{di|d1,d2,…,dn}构造虚拟斥力场的思想，在无人机接近障碍物时给以较大的惩罚，而在远离障碍物时给以较小的惩罚，在未检测到障碍物时惩罚为0，设置单步惩罚函数的数学形式为：

(17)

式中αso为障碍物惩罚系数。在面对具有避障功能的移动障碍物时，基于碰撞域提出一种考虑碰撞时间的惩罚函数设计方法。为了方便计算，将障碍物与无人机形状简化为其最小外接圆。如图4所示，其中va,ra分别为无人机速度矢量和半径，vb,rb分别为障碍物速度矢量和半径。

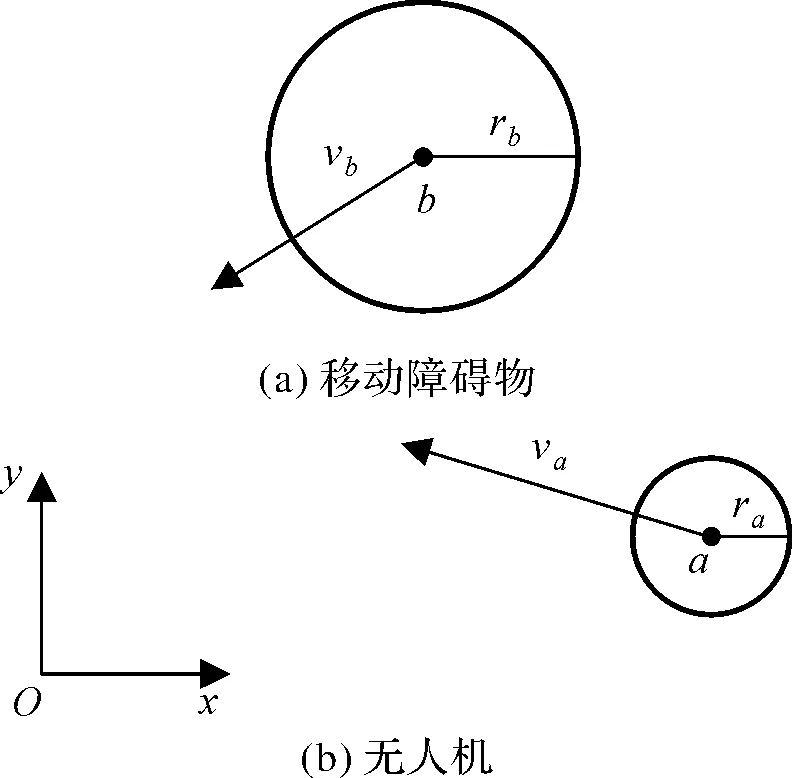
图4 无人机与移动障碍物示意图

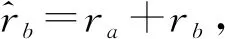
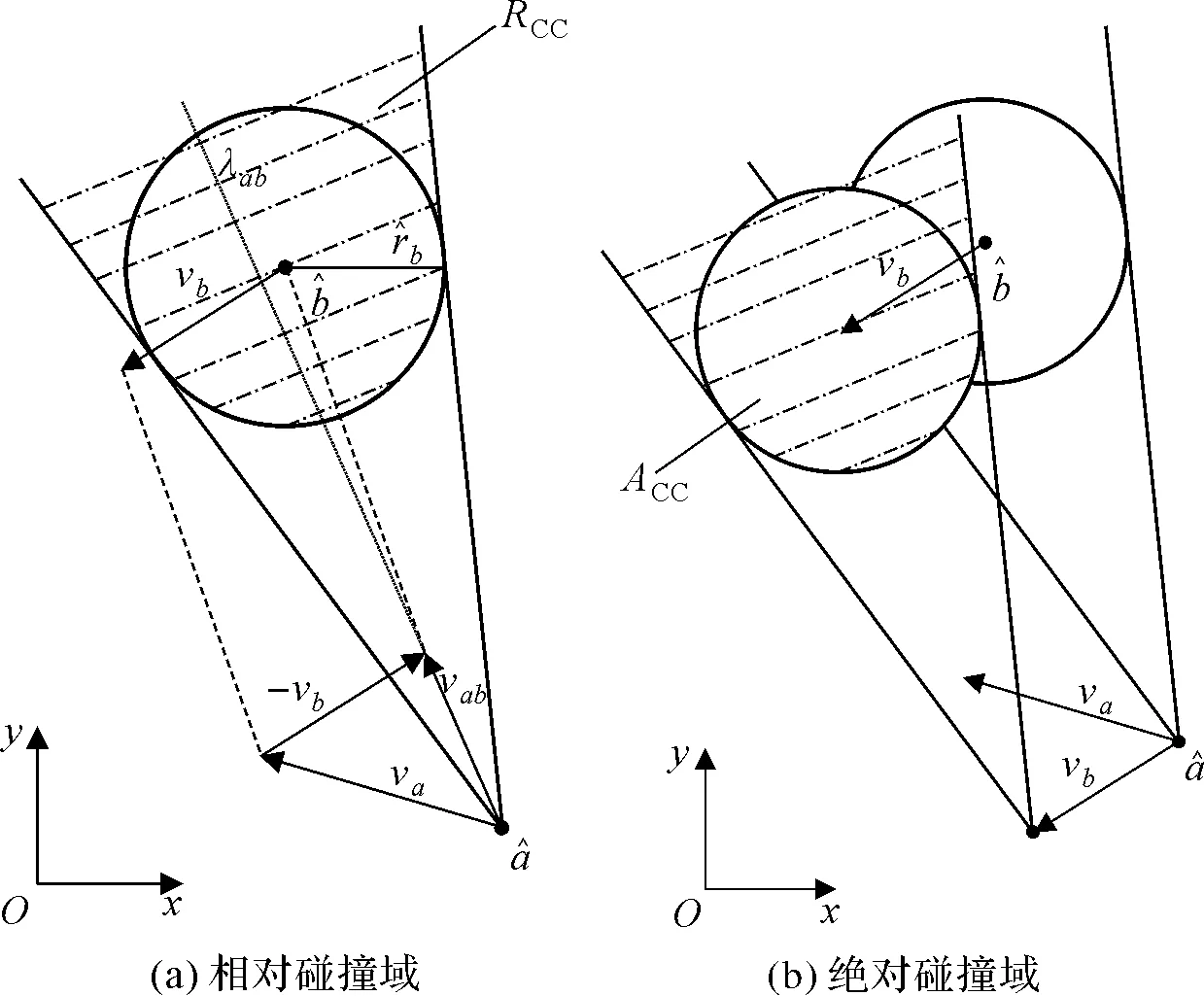
图5 碰撞域示意图

(18)

ACC=RCC⊕vb

(19)

根据碰撞域的数学形式，当无人机的线速度矢量处于碰撞域ACC内时，经过时间tc，智能体将与移动障碍物发生碰撞。基于预期碰撞时间的单步惩罚函数构造为：

(20)

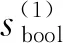
ro=rso+rvo

(21)

此外，为了缩减训练时间使其更快收敛，在无人机撞到障碍物或边界时将得到稀疏惩罚：

(22)

2)快速追踪奖励函数

复杂环境下追踪目标需要无人机以较短的时间完成避障导航并快速进入目标跟踪范围，因此在避障导航阶段决策网络需要提供较大的速度决策量，设置单步奖励函数为：

(23)

rt=-αtkLk

(24)

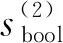
rf=rv1+rt

(25)

此外，为了鼓励无人机到达跟踪范围，在完成避障导航后，给以稀疏奖励：

(26)

3)跟踪性能奖励函数

为了实现更精准的无人机地面目标跟踪，需要使跟踪阶段的无人机具有与目标接近的速度，且在二维平面上无人机与目标的距离越小代表跟踪性能越好。因此设置基于速度、距离和角度的奖惩函数分别为：

(27)

rL=αL(Lk-1-Lk)

(28)

(29)

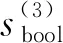
rc=rv2+rL+ra

(30)

将以上奖惩函数按照重要性分配权重系数，则总奖惩函数的数学表达形式为：

r=woro+wfrf+wcrc+rdone1+rdone2

(31)

2.3 基于IMM-PPO的目标追踪策略训练

PPO算法采用了Actor-Critic网络，这种网络结构能够同时进行值函数与策略函数学习，其中Actor学习策略函数，Critic学习策略的近似值函数。

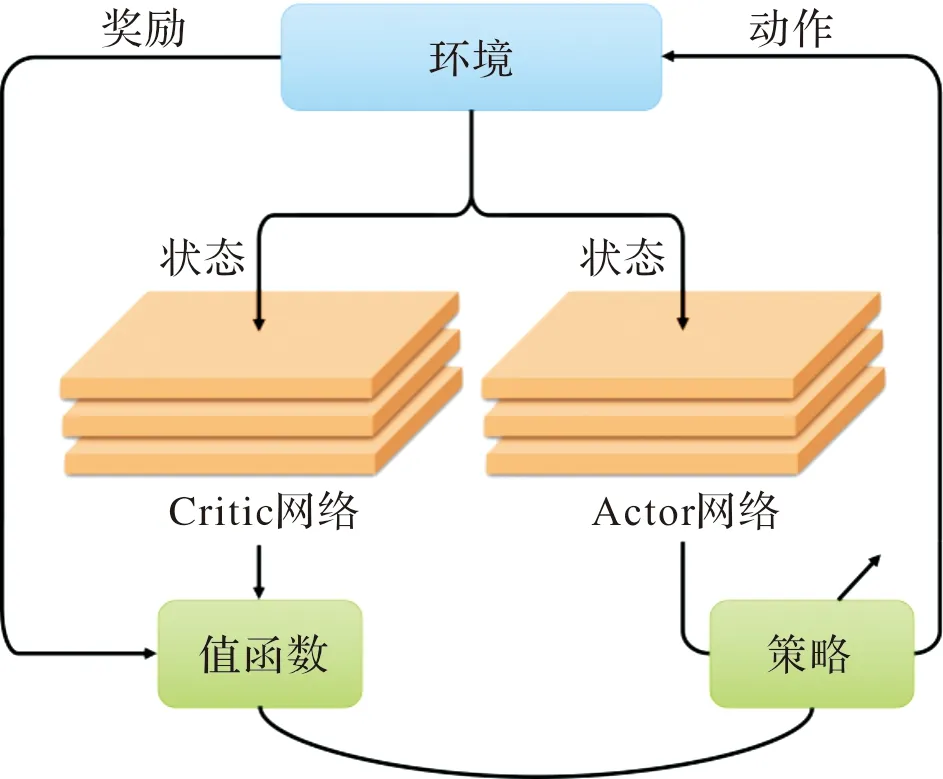
图6 Actor-Critic网络

在Actor-Critic框架下的策略更新[13]可以表示为：

(32)

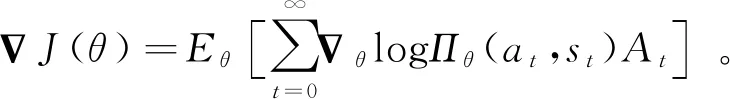
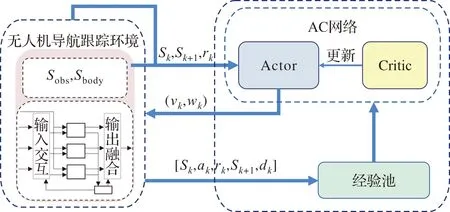
图7 无人机导航跟踪策略训练框架

Actor网络用于接收智能体与环境交互的状态信息St=(Sbody,Sobs,Star)，并输出动作(v,w)的采样Dt，Critic网络通过对优势函数的估计来评估策略的优劣。网络权重及学习参数的更新本质上是学习关于(a,s)的策略函数，将待优化的导航跟踪策略函数近似参数化：

Π(a|s)～Πθ(a,s)

(33)

式中：a为无人机动作(v,w)；s为状态信息St。通过策略梯度算法对策略参数进行基于梯度的优化[14]，定义策略梯度估计为：

(34)

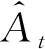
(35)

式中：VΠ(st)表示无人机在t时刻下的状态st时采用策略Π的价值；Rt′表示在t′时刻智能体得到的奖励；γ为奖励折扣因子。无人机导航跟踪策略更新的目的是寻找到一个优于原策略Πθ的Π′θ，以旧的策略Πθ与环境交互，将采集到的样本用于更新策略Π′θ，为了防止新旧策略相差过大，使用一种截断方式限制策略更新。因此采用优势函数估计描述策略更新的目标函数表示为：

(36)

式中：Π′θ为新的策略，ε为超参数。clip()函数用来将新旧策略的比值限定在(1-ε)与(1+ε)之间，具体函数形式如图8所示。

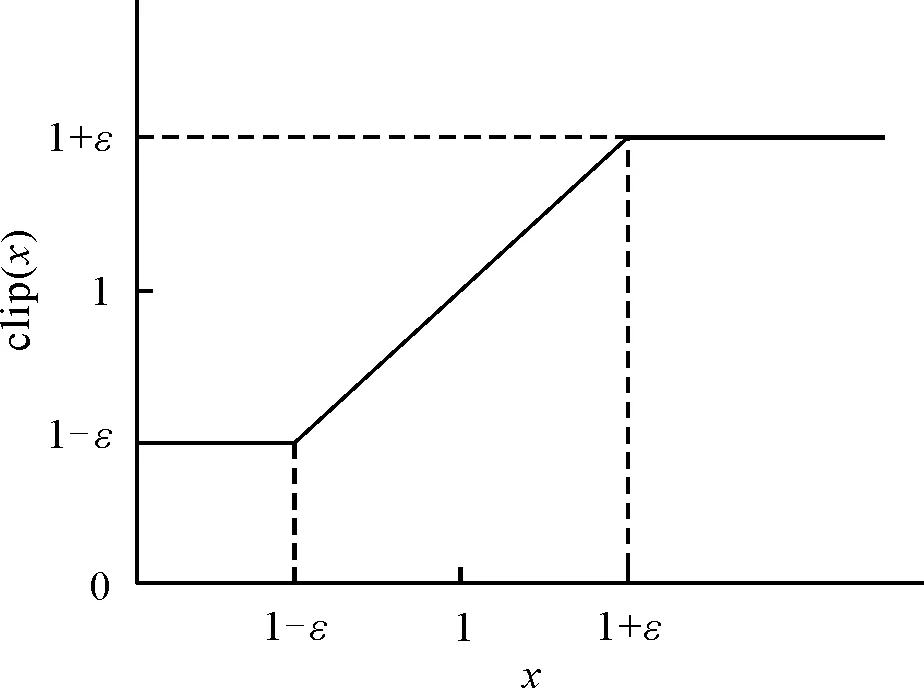
图8 截断函数示意图

若在t时刻采取动作at的回报大于平均回报，即优势函数为正，则增大该动作概率，反之减小该动作概率。

2.4 无人机目标追踪策略网络决策

对网络权重参数训练完成后，决策网络将无人机与环境交互采集到的状态信息St=(Sb,So,Star)=(s1,s2,…,sn)作为输入，其中n为状态空间维度。采用权重参数和偏置计算网络输入的加权和，并得到神经元的输出，其表达式为：

(37)

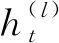
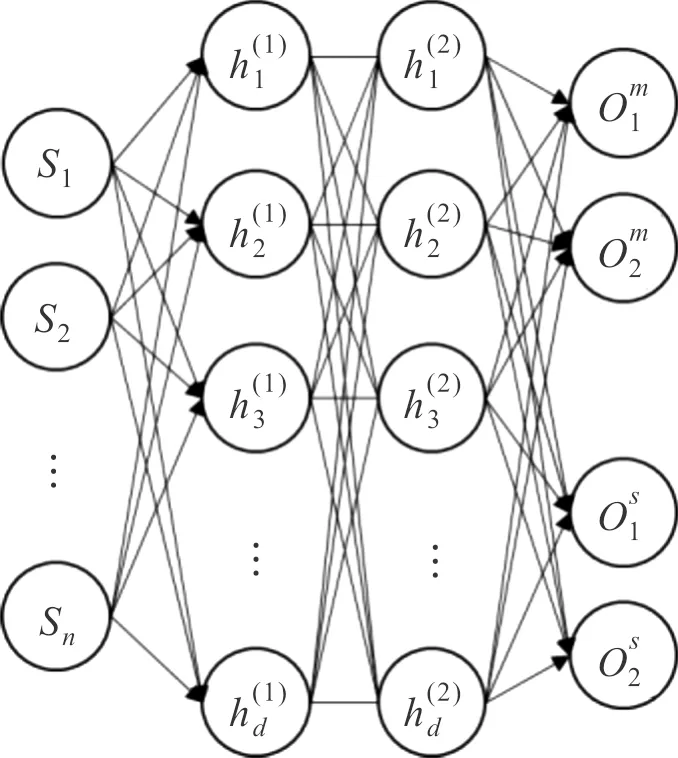
图9 决策神经网络结构图

3 仿真验证

为验证IMM-PPO算法在无人机追踪任务上的有效性，进行仿真实验。首先进行仿真环境的搭建以及参数设置，然后分析了策略训练过程中强化学习算法的奖励变化曲线，最后分别采用IMM-PPO算法与DWA算法进行无人机机动目标追踪仿真实验，比较两种算法的性能。

3.1 仿真环境

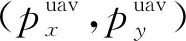
3.2 基于IMM-PPO的无人机跟踪策略训练

采用IMM滤波算法对目标状态进行估计，将估计值作为强化学习算法状态空间的一部分进行无人机跟踪策略训练。训练过程中的回报随回合数变化如图10所示。

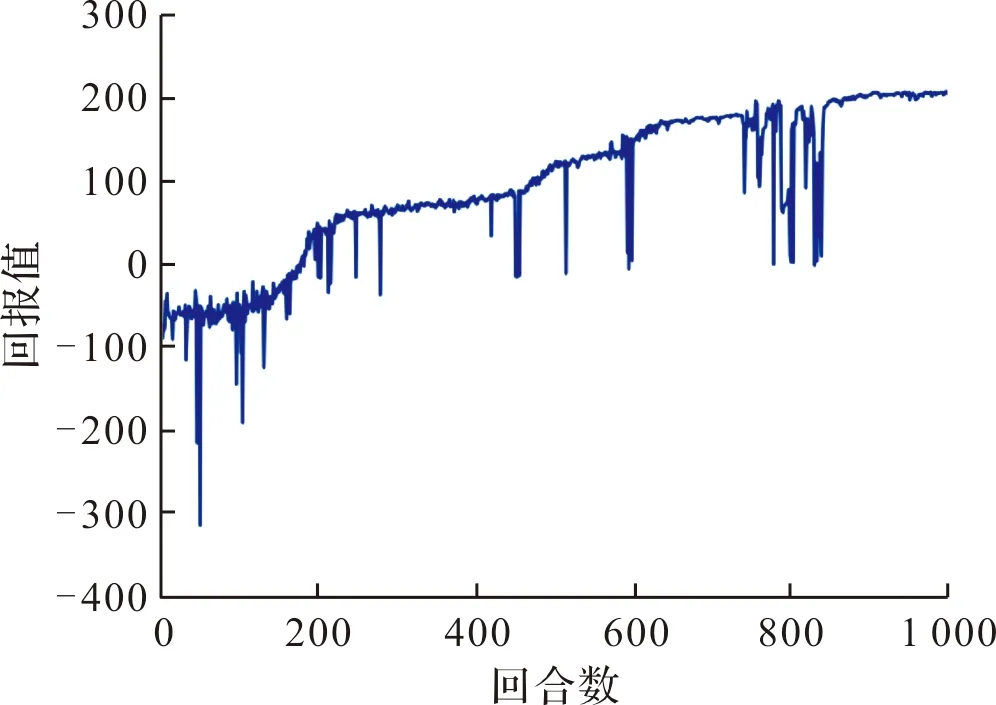
图10 奖励变化曲线

从图中可以看出，在训练初始时刻，无人机在复杂环境中处于探索阶段，得到的回合奖励较少。在多个回合训练后，无人机逐渐具备避障跟踪能力，能够与障碍物保持安全距离并缩短与目标之间的最小距离，回报呈逐渐上升趋势。在900回合后无人机避障跟踪决策网络权重趋于收敛，表明无人机能够在奖励函数的指引下学习到最优的跟踪策略。

3.3 与传统DWA算法对比

为了突出IMM-PPO算法在障碍物环境中追踪机动目标的优越性，与传统DWA算法作比较，设置两种算法下无人机具备相同的初始状态以及约束条件，在同样的环境中追踪运动模式相同的机动目标。

3.3.1 快速性对比

针对单位时间决策网络的动作输出，给出IMM-PPO算法和DWA算法下的无人机避障导航的过程图如图11所示。

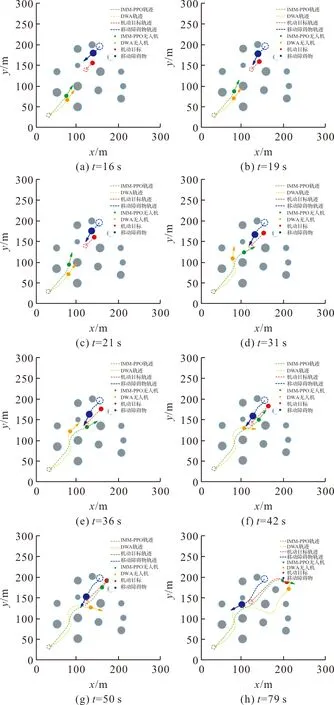
图11 避障导航过程图

从图中可以看出，IMM-PPO算法与DWA算法均能指引无人机躲避障碍并到达目标跟踪范围。在t=16 s时，IMM-PPO算法下的无人机检测到障碍物并调整偏航角，在奖励函数的引导下以较快的速度躲避障碍并飞往下一个跟踪点，如图11(a)所示。在t=21 s时DWA算法下的无人机检测到障碍物并判断后续k步的路径指标函数，选择最优的避障路径，并在t=31 s时完成避障，如图11(d)所示。从t=36 s至t=42 s，IMM-PPO决策网络根据环境信息预测的碰撞时间，结合快速追踪的奖励函数，调整输出的动作，使无人机能够快速且以较低代价远离碰撞域，如图11(e)、图11(f)所示。t=50 s时，IMM-PPO算法下的无人机到达机动目标的跟踪范围并开始执行跟踪任务，而在t=79 s时，DWA算法指导的无人机才进入目标的跟踪范围，如图11(g)、图11(h)所示。两种算法下无人机完成追踪避障并进入目标跟踪范围的路径长度如表1所示。

表1 IMM-PPO与DWA避障导航路径长度比较

3.3.2 跟踪性能对比

为了体现IMM-PPO在跟踪性能方面的优势，无人机飞行过程中的速度控制量和目标相对距离变化曲线及跟踪任务轨迹分别如图12～图14所示。

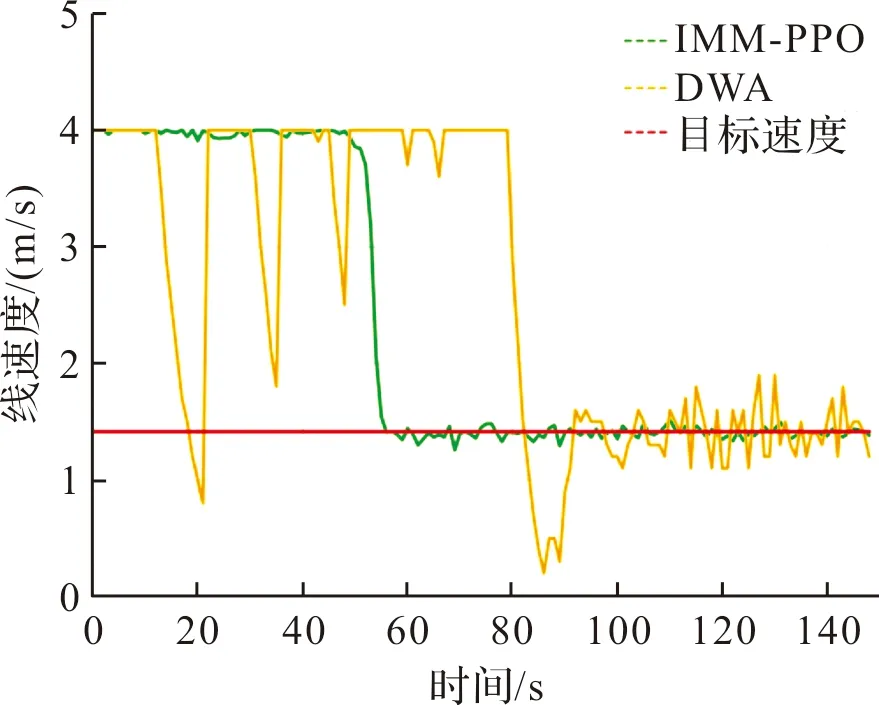
图12 IMM-PPO，DWA速度变化图

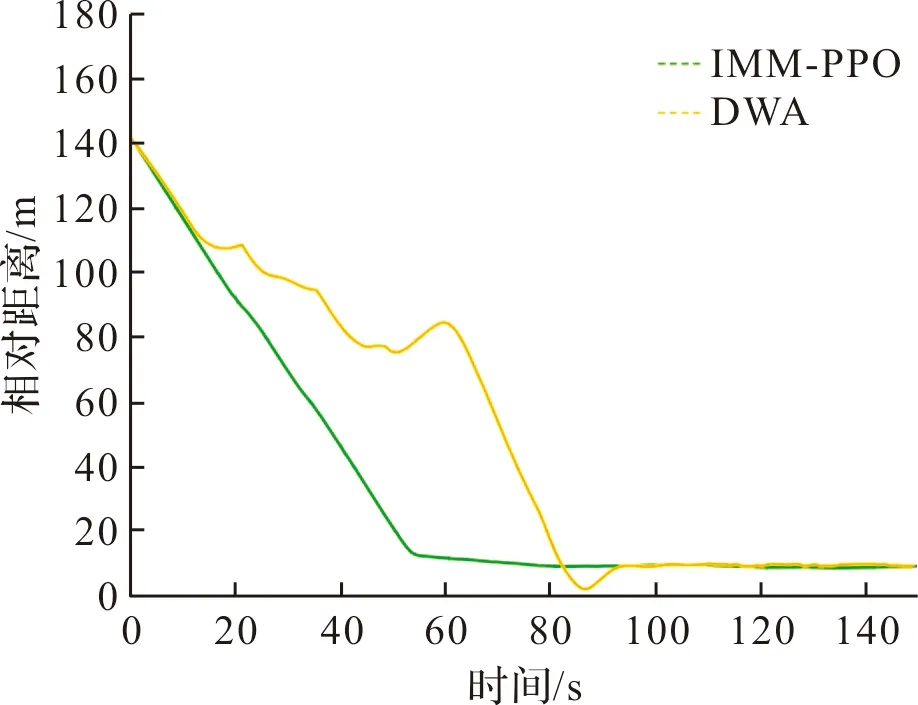
图13 无人机与目标相对距离图

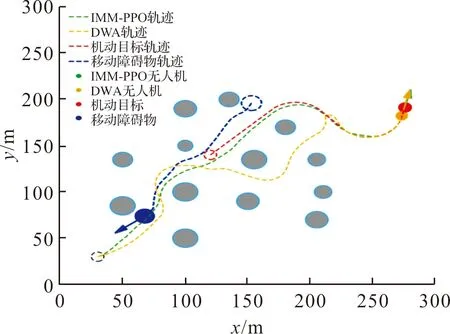
图14 机动目标跟踪任务轨迹图

从图12可以看出，在任务起始时刻，IMM-PPO算法与DWA算法都输出较大的速度控制量，从而使无人机能够快速接近目标，在检测到障碍物并进入避障任务环节时，IMM-PPO算法的速度控制量仍旧稳定在最大允许速度附近，而DWA算法下无人机的速度控制量具有较大振幅。当任务进行到跟踪阶段，即无人机到达机动目标的跟踪范围内时，IMM-PPO策略网络输出一个接近机动目标真实速度的速度控制量进行跟踪，并且直到仿真结束均能够稳定在目标速度附近；而DWA算法下的无人机速度振荡明显，无法达到稳定在目标速度附近的跟踪效果。图13描述了任务过程中无人机与目标相对位置变化，可以看出，从t=50 s至t=149 s，IMM-PPO决策网络能够使无人机以平稳的速度稳定在跟踪范围内，相比于DWA算法，IMM-PPO算法下的无人机具有更多的有效跟踪步数。图14展示了从初始时刻到最大时间步数的无人机运动轨迹，从图中可以看出，IMM-PPO算法下的无人机具有更加平滑的运动轨迹，DWA算法牺牲了部分跟踪性能而进行避障，轨迹具有较明显的突变。根据以上结果分析，基于IMM-PPO算法的无人机在线避障跟踪策略明显具有更好的跟踪性能。

3.4 强化学习在线跟踪策略

为了进一步体现IMM-PPO的在线感知避障跟踪能力，改变环境中障碍物的大小，分别设置无人机与移动障碍物位于与上述仿真不同的初始位置(110 m,10 m)，(182 m,204 m)并且移动障碍物具有不同的避障轨迹，仿真结果如图15所示。

由图15可以得到，无人机能够在无碰撞的情况下，在41 s时到达目标跟踪范围执行跟踪任务并始终保持与目标的相对距离在20 m内。由此可以看出，在环境改变的情况下，训练后的无人机避障跟踪策略网络仍然能够指导无人机进行静止与移动障碍躲避并跟踪机动目标。

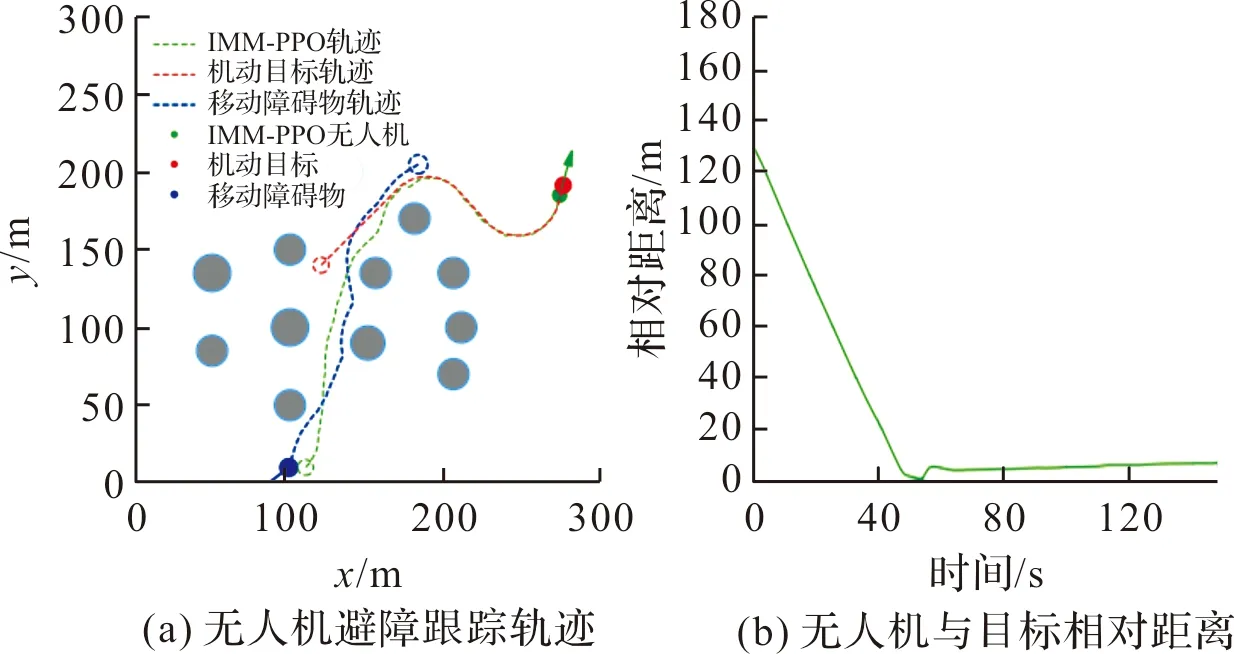
图15 不同环境下的无人机在线避障跟踪仿真

总之，传统的避障算法DWA能够通过指标函数选取最优的无人机控制量(v,w)，但在面对复杂障碍物时将得到较大的减速度，从而无法保持较高的速度追踪机动目标，延长了无人机导航的路径长度与耗时，在执行跟踪任务时无法保持与目标接近的速度。而文中所提算法能够在线自适应调整动作，根据无人机与移动障碍的预期碰撞时间避免其在追踪过程中陷入碰撞域内，从而快速躲避障碍物并到达目标跟踪范围，在跟踪目标时速度能够稳定在目标速度附近，更适用于无人机机动目标跟踪场景。

4 结论

针对复杂环境下无人机机动目标追踪的问题，提出一种基于IMM-PPO的目标追踪策略，首先采用交互式滤波算法对机动模型进行滤波估计，接着根据优化目标及约束设计奖惩函数，并对策略网络权重进行训练，训练好的神经网络根据智能体与环境交互得到的信息更新输出动作的概率分布，在避开静止与移动障碍物的前提下在线完成快速导航并对机动目标进行稳定跟踪。从仿真结果来看，相较于传统避障算法DWA，文中所提算法能够兼顾目标跟踪过程的安全性、快速性并且能够保持更好的跟踪性能，在环境改变时也能够执行目标追踪任务，具备一定的泛化性。