基于改进速度障碍算法的无人机反侦察路径规划研究
冒 燕,杨家鼎,徐小强
(武汉理工大学自动化学院,武汉 430070)
0 引言
无人机(UAV)已广泛应用于情报侦察、火力摧毁、安防应急、电力巡检、农林植保等军民用领域[1],在军事应用方面,未来作战模式对武器装备的苛刻要求,无人机具有无人员伤亡事故、使用限制较小、隐蔽性好、效费比高等优点,在现代战争中的地位和作用日渐突出[2]。路径规划是无人机自主飞行的关键技术之一[3],若要无人机更好地执行预定航行任务,其使用的路径规划算法应能够快速适应动态变化的复杂电磁环境,即避免进入雷达的探测范围,将无人机反雷达侦察看成规避障碍物,而路径规划算法的优劣主要体现在如何准确规避静态和动态障碍物上[4]。
针对无人机路径规划的最小路径、方向调整等问题,国内外学者相继开展了一系列研究工作[5-7]。Liu等[8]提出了一种混合差分共生生物搜索(HDSOS)算法,对共生生物搜索(SOS)的互利相位和寄生相位进行了改进,引入了牵引函数的概念,对静态障碍物有较好的避障规划,但没有考虑动态障碍物;陈良剑等[9]提出了一种基于快速随机搜索树(RRT)的动态规避航迹规划算法,通过引入启发因子和动态调试的方式加强了算法的指向性,在障碍物密集的环境下有较优秀的表现,但在复杂情况下耗时较长;Liu等[10]提出了一种基于改进t分布的进化算法对航迹规划的导引函数进行连续优化,对于复杂未知地理信息条件下航迹规划具有良好的实用性,以上3种算法都仅考虑了对单一或复杂静态障碍物避障的影响因素,忽略了对动态障碍物的避碰;王宏伟等[11]采用速度障碍法同时调速和调向,基于最小调整量原则,实现与动态障碍物的冲突解脱,但并没有考虑多种静态障碍物的复杂场景;陈方正等[12]基于动态窗口法,将测向定位目标函数由单步最优原则扩展到对多步预测航迹的评价,增强了对静态和动态障碍的预判能力,使其规避更迅速,但当多步设置较大时会需要更高的算力;袁建华等[13]提出了一种基于改进粒子群算法与滚动策略相结合的路径规划算法,通过加入信息素与启发函数增强全局搜索能力,可以较好的对静态和动态障碍物进行规避,但在复杂环境下实时性不够好,虽然以上两种算法都能避开动态障碍物,但不能明确指定从何方位进行规避,也无法对动态障碍物的避碰边界范围做出精确判断。
综合上述分析,文中将无人机路径规划中面临的雷达反侦察问题描述为无人机在明确避碰范围下如何对动态和静态障碍物的避障问题,提出一种基于改进速度障碍法并结合人工势场法对动态和静态障碍物在明确的安全边界中进行路径规划,该算法可以对障碍物边界范围提前进行较为精确的避障,具有操作简单、易于实现和实时性好的特点,进而提高无人机在避碰中的稳定性。
1 改进速度障碍法
1996年,Fiorina等[14]将速度避障运用在动态环境的路径规划方面,基本思想是通过动态障碍物的速度大小和方向提前对其从指定方向进行避障。
设无人机A的安全范围半径为RA,动态障碍物B的安全范围半径RB,通过相对范围,将动态障碍物的威胁区半径扩大为RA+RB,由无人机A的位置和威胁区可以得到障碍锥,如图1(a)所示,当无人机与动态障碍物的相对速度落入障碍锥时,则表示在该速度下运动必会发生碰撞。
当相对速度落入速度障碍锥后,并不会立即进行避障,而是两者到达某一安全距离时,再重新选择速度方向。在世界坐标下设无人机坐标为(Xa,Ya),动态障碍物坐标为(Xb,Yb),需要重新对障碍物的位置和速度进行坐标系变换,使其以无人机为相对参考系,相关计算为:
l1:y=tan(α+β)(x-xvb-Xa)+(yvb-Ya)
(1)
l2:y=tan(α-β)(x-xvb-Xa)+(yvb-Ya)
(2)
(3)
式中:α为无人机与障碍物位置连线与参考坐标系水平正轴夹角;β为速度障碍锥的二分角;l1与l2为两个射线方程;C为无人机可达速度圆方程;va为世界坐标系下的无人机速度矢量的模。
将式(1)、式(2)分别与式(3)联立可得到候选速度,如图1所示,(a)图中va1和va2为速度避障法得出的临界避碰速度,分别从障碍物后方和前方避障,(b)图中vL和vR分别为无人机最大偏转角对应的速度。

图1 速度障碍模型与无人机模型
障碍物以陆基雷达和机载雷达为例,无人机较机载雷达优先从其后方绕行避免被侦察,故需要选择与机载雷达速度方向夹角较大且当前速度夹角较小的候选速度。
改进速度障碍法通过障碍锥进行速度的提前选择对动态障碍物实现从不同方位的避障,具有较精确的安全避障距离,然后结合人工势场法对静态障碍物进行不同决策。
2 改进人工势场法
1986年,Khatib等[15]首先将人工势场理论运用在智能路径规划领域,其主要思想是将机器人的感知环境看作一个虚拟的力场,障碍物或具有威胁的区域对机器人产生斥力,目标点对机器人产生引力,机器人便可以在其合力下向目标点前进。在人工势场中建立引力场和斥力场,将机器人和障碍物简化为圆点方便于分析。
传统人工势场法具有陷入局部最小陷阱和目标点不可达问题,其常用斥力场函数为:
(4)
式中:ρ(q,qobs)为无人机与障碍物距离;ρ(q,qgoal)为无人机与目标点距离;ρ0为斥力势场的影响范围;Krep为斥力增益系数。
Krep可表示为:
(5)
为克服传统算法的陷入局部最小陷阱和目标点不可达问题,文中引用改进的人工势场法[16],其斥力函数可表示为:
(6)
(7)
(8)
式中m为斥力势场因子,通常取0.5。
无人机的引力采用速度障碍法的选择速度,根据无人机和障碍物的位置关系,改变斥力正交后的方向实现从静态障碍物较短弧长一侧进行避障,以达到较短路程的目的,并实现在安全距离内对静态障碍物进行精确平滑避障。
3 仿真场景设置
3.1 雷达场景设置
针对在实际对雷达的检测中无人机会出现来自传感器系统误差的白噪声,对采样点使用平滑滤波器进行小批量处理来判断动态和静态障碍物,再将数据输入算法中。
将无人机对不同雷达边界检测划分为3种场景:
1)陆基雷达和机载雷达的检测边界没有重叠,无人机分别避开两种类型障碍物,并且目标点靠近陆基雷达;2)陆基雷达和机载雷达的检测边界存在重叠,无人机首先进入陆基雷达影响范围,同时调整速度方向对陆基雷达进行避障;3)陆基雷达和机载雷达的检测边界存在重叠,无人机首先对机载雷达进行速度选择,在避开机载雷达途中对陆基雷达进行避障。
将无人机、陆基雷达和机载雷达的边界判断划分为以上场景,方便对复杂场景多个小场景拆分后再进行选择避障。
3.2 无人机反雷达侦察最大距离的确定
算法仿真中的静态障碍物为地面静止的陆基雷达或海上慢速移动的舰载雷达,动态障碍物为空中机载雷达[17],其速度参考全球鹰无人机速度,取为100 m/s。避障半径为雷达对无人机的最大探测距离,其数学模型Rmax可描述为[18]:
(9)
式中:Pt为雷达的发射功率;G为雷达天线的增益;λ为雷达信号的波长;Simin为雷达接收机的灵敏度;σ为无人机的雷达截面积(RCS)。
设某部舰载雷达的Pt,G,λ,Simin分别为5×105W,30 dB,0.1 m,-90 dBm,无人机通过雷达隐身技术设计后的RCS降为0.1 m2,通过雷达探测距离的数学模型可以计算雷达探测距离约为20 km。
3.3 无人机参数确定
算法仿真中以以色列的哈比无人机[19]为例,哈比无人机是世界上性能最为先进的反辐射无人机之一,设无人机在二维水平面的速度为50 m/s、半径为2 m、巡航范围为300 km。
3.4 算法流程
算法流程如图2所示,无人机在给定检测范围对雷达进行检测,通过雷达边界进行判断,若无人机将雷达判断为机载雷达,则使用速度障碍法重新选择无人机速度方向,若为陆基雷达则用改进人工势场法进行避障;在两者边界重合范围时,无人机在可达速度范围内选择能够同时远离机载雷达和陆基雷达的方向,并通过速度障碍法重复进行修正。当无人机离开雷达范围后,无人机选择指向目标点的偏航方向以保证最短时间和路程。

图2 算法流程图
4 算法仿真验证及结论分析
为验证本算法的实际效果,通过数学仿真软件依次对3.1节中的3个场景进行仿真模拟。主要仿真参数设置如表1所示,其中机载雷达方向以X正轴逆时针计算,步长设置不宜过大,以免导致无人机与雷达距离突然减小而斥力快速增大使无人机大幅度偏航,连续性下降。设置人工势场作用范围半径为雷达侦察半径的2.2倍。斥力场增益K的数值越大,无人机受到的势场影响程度也就越大,此处设置增益K为人工势场作用范围的2倍。

表1 无人机避障仿真主要参数
仿真结果如图3~图8所示,图3、图5和图7的场景仿真结果中的虚线圆表示雷达探测范围。图4、图6和图8中的图(a)为无人机偏航方向和大小,以地图X正轴逆时针方向为正;图(b)为每步的方向改变量,即对图(a)中数值进行梯度运算;图(c)中无人机与雷达距离在小于40 km时进行显示,过远距离显示为0 km。表2数据为3种仿真场景中的无人机路程以及与各个雷达的最小距离。

图3 场景1的仿真结果

图4 场景1中角度量以及与障碍物最小距离
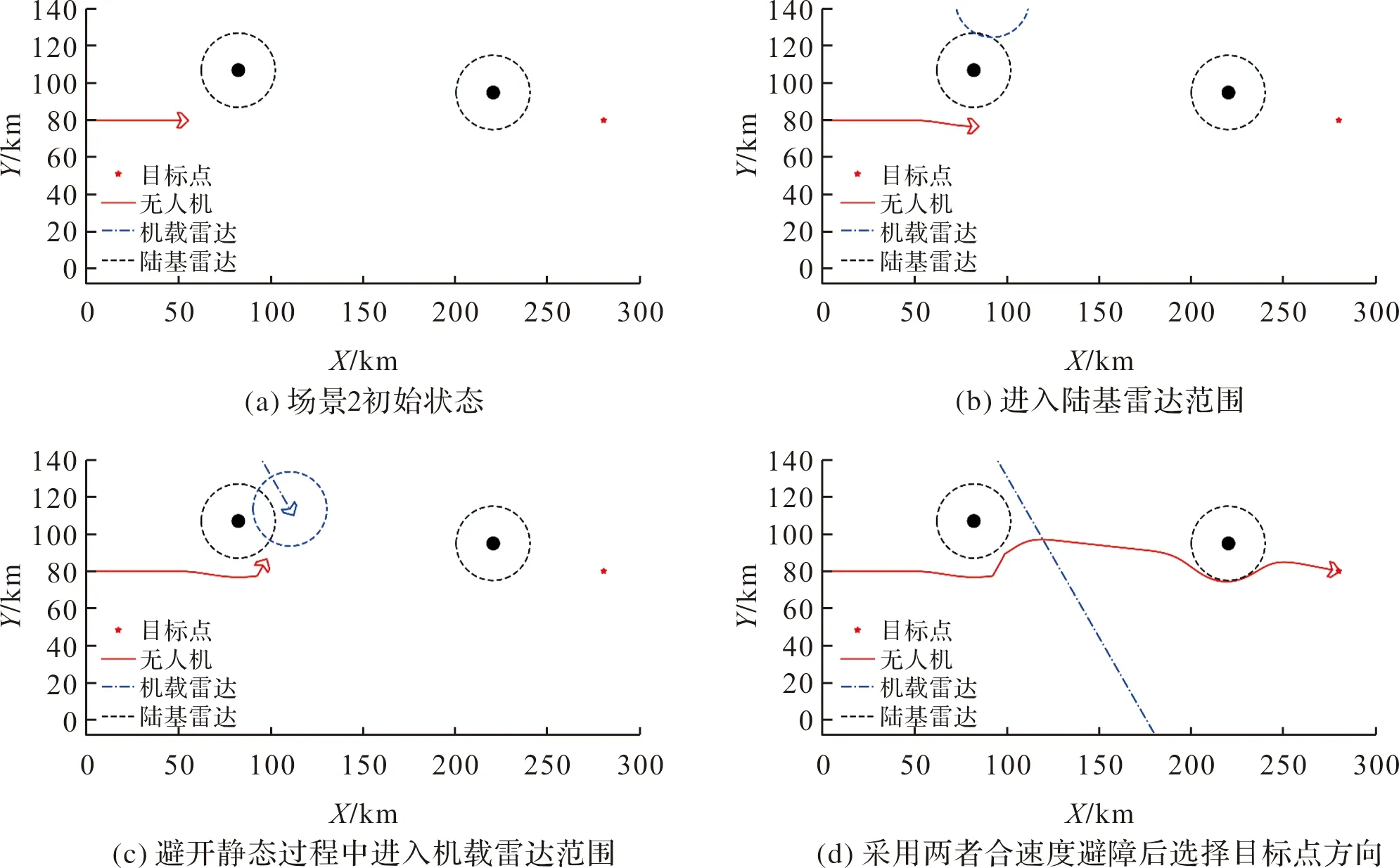
图5 场景2的仿真结果

图6 场景2角度量以及与障碍物最小距离

图7 场景3的仿真结果

图8 场景3角度量以及与障碍物最小距离
场景1仿真结果如图3所示,无人机首先在图3(b)中检测到机载雷达并通过速度障碍法重新选择速度从后方避开,然后在图3(c)中避开之后选择指向目标点的速度方向,途中检测到陆基雷达,最终无人机通过改进人工势场法顺时针绕过陆基雷达到达目标点,如图3(d)所示。
场景2仿真结果如图5所示,根据图5(b)中的无人机路径可知,无人机首先检测到陆基雷达,由于雷达中心位置相对无人机位置偏右,故使用人工势场法以顺时针从较短的弧长方向进行避障,然后在速度障碍法和人工势场法的共同作用下速度平缓行驶一段后进行避障,如图5(c)所示,当无人机绕过机载雷达后再选择目标点方向的速度,最终到达目标点,如图5(d)所示。
场景3仿真结果如图7所示,无人机首先检测到机载雷达并通过速度避障法重新选择速度进行避开;在避开途中检测到陆基雷达,且在陆基雷达周围存在机载雷达,故无人机通过人工势场法选择逆时针避开陆基雷达;在无人机避开第一个陆基雷达和机载雷达后继续避开第二个陆基雷达并到达目标点,以上3个阶段分别如图7(b)、(c)、(d)所示。
由图4、图6和图8的图(a)可得无人机的偏航角较为稳定,没有出现抖动;在图(b)中,由于避碰机载雷达时由速度避障法对速度方向进行选择以及在避开机载雷达后重新对速度方向选择,故存在两个明显的在限制范围内的偏航角改变量;结合图(c)和表2可得,在3个场景中无人机与陆基雷达和机载雷达的安全距离都符合要求,且具有较短的仿真路程。

表2 3种场景下的仿真数据结果 单位:km
综上仿真结果可得,文中算法在避碰陆基雷达和机载雷达中能够得到一条完整的规划路线,其通过速度障碍法对机载雷达进行速度提前选择的方案以及人工势场法能实时避碰陆基雷达的优势,可保证合适的安全距离范围内具有较精确的规划路程。
5 结语
针对无人机避碰复杂动态和静态障碍物时的速度选择问题,提出了一种在二维平面交替使用速度避障和改进人工势场法的局部路径规划方法。仿真结果表明,无人机可以在安全距离范围内以及较短路程下对陆基雷达和机载雷达进行避碰,且具有较好的实时性。该算法可以提高无人机的自主控制能力和复杂电磁环境中的反侦察能力,保证无人机顺利完成预定的侦察、干扰或摧毁等规划任务。
上述研究结果是基于特定场景而研究的,没有考虑最大俯仰角以及飞行高度要求的情况,未来可优化速度障碍法和人工势场法,使其在三维空间中进行使用,更加符合实际情况。此外,将雷达侦察范围作为动态和静态障碍物简化为圆形区域,很大程度上简化了计算,实际应用中,可结合实际区域的地形、恶劣天气等约束条件,设置更多的障碍物,考虑不规则障碍物作为实验模型。文中算法属于一种局部路径规划方法,可在大型航空地图中结合其他全局算法,采用分段处理达到避障的效果。

