基于模糊马尔可夫链的奖惩系统*

南京信息工程大学数学与统计学院 张雨晴 董英华

现有文献中，通常在一个精确的模型下对奖惩系统进行研究，忽略了奖惩系统中的不确定性。本文在索赔次数服从泊松分布的假设下，把分布参数量化成一个三角模糊数，将不确定性考虑进奖惩系统中。利用模糊马尔可夫链来研究奖惩系统，并通过模糊转移概率矩阵计算得到模糊稳态概率分布。将其与普通稳态概率分布对比，发现模糊稳态概率分布的1截集与普通稳态概率分布相等，验证了普通奖惩系统是模糊奖惩系统的一个特例。从严厉性方面对奖惩系统进行比较，发现普通奖惩系统相较于模糊奖惩系统略严厉些。

在汽车保险中，通常用奖惩系统对先验费率进行调节，使得投保人缴纳的保费反映真实的风险水平，因此奖惩系统在车险费率厘定中占据重要位置。奖惩系统是根据保单的历史索赔数据对续期保费进行调整的机制，即对上年或连续多年无索赔发生的投保人，续保时降低保费；对上年发生索赔的投保人，续保时提高保费。在我国，这种制度又称为无赔款优待系统。

现有文献中，多数在索赔次数或索赔额服从一个精确分布的条件下研究奖惩系统。Frangos等[1]在泊松-伽玛分布假设下，利用先验风险特征和索赔次数信息结合广义线性回归模型建立奖惩系统。孟生旺[2]在二项-贝塔分布和负二项-贝塔分布的假设下，分别建立奖惩系统。孟生旺和张永霞[3]在累计索赔额服从零调整逆高斯分布的条件下，结合风险特征信息研究奖惩系统。对模型中存在的不确定性，Adillon等[4]将参数量化成模态区间，在索赔次数服从泊松分布的条件下对奖惩系统进行研究。Villacorta等[5]引入模糊数对索赔次数分布的参数进行量化。

实际应用中，索赔次数或索赔额的模型中往往包含不确定性，这种不确定性可能由随机性等原因造成的。因此本文在索赔次数服从泊松分布的假设下，采用Villacorta等中的方法，将分布参数量化成三角模糊数来研究奖惩系统。下文中，将基于模糊马尔可夫链的奖惩系统称为模糊奖惩系统。在给定转移规则的条件下，利用模糊转移概率矩阵计算模糊稳态概率分布。用相对稳定平均水平、对新投保人的隐性惩罚和变异系数指标从严厉性方面比较普通奖惩系统和模糊奖惩系统，发现模糊奖惩系统的严厉性略低于普通奖惩系统。

1 奖惩系统

奖惩系统中包含保费等级、奖惩系数和转移规则[3，6]。

(1)保费等级。假设有s个保费等级，对新加入的投保人，进入初始保费等级。

(2)奖惩系数。第i个保费等级的奖惩系数为ri(i=1，2，...，s)。保费等级越高，奖惩系数越高，反之。其中，初始保费等级的奖惩系数为1。

(3)转移规则。已知投保人索赔次数的情况下，决定投保人从原保费等级转移到新保费等级的规则。

本文采用常用的-1/+2转移规则，即投保人在上一投保期无索赔发生，续保时下降1个保费等级，若发生索赔，那每发生1次索赔，续保时上升2个保费等级。该转移规则如表1所示（i，j，k均为整数）：

表1 -1/+2转移规则Tab.1 -1/+2 transition rules

从表1可以看出，投保人最多上升（下降）到最高（低）保费等级。投保人在某一投保期内从保费等级i转移到等级j的概率Pij(pij≥0)称为一步转移概率，矩阵P=(pij)称为转移概率矩阵。保单组合经过若干个投保期后，各保费等级的分布将趋于稳定，此时各保单所处状态称为稳定状态，其概率分布称为稳态概率分布π=(π1，...，πs)，满足式(1)[7]：

2 模糊马尔可夫链

2.1 模糊数

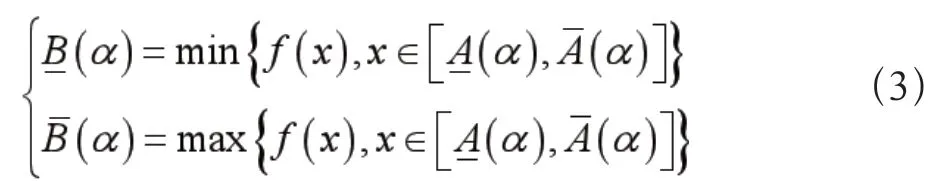
2.2 模糊马尔可夫链

采用模糊马尔可夫链进行研究时，只是在普通马氏链的基础上，将状态变为模糊状态或将转移概率矩阵变为模糊转移概率矩阵。本文采用后一种方法进行研究。

设{Xn，n=0，1，2，...}是一个马氏链，对应的转移概率矩阵为P=(pij)。若P=(pij)中的一些概率pij存在不确定性，则可通过模糊数来量化。此时P=(pij)转变成模糊转移概率矩阵其中通过获得的稳态概率分布称为模糊稳态概率分布的α截集为满足

3 实证分析

本文用澳大利亚某保险公司一年期的车辆保单数据进行实证分析，该数据可从文献[10]中获得，数据中保单索赔次数信息如表2所示。

表2 保单索赔次数信息Tab.2 Number of claims information

计算得该组数据均值约为0.07，方差约为0.077，均值与方差相差较小，可用泊松分布拟合。假设索赔次数N服从参数为λ的泊松分布，即N～P(λ)，概率分布为

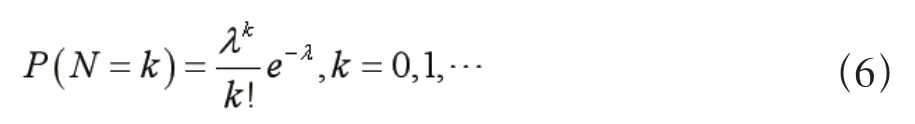
用极大似然法求得参数λ的估计值为0.07，故本文中的索赔次数N～P(0.07)。

本文采用我国2015版奖惩系统的保费等级及奖惩系数数据（如下表所示）进行研究，数据可从文献[11]中获得。由表1可得奖惩系统的具体转移规则如表3所示。

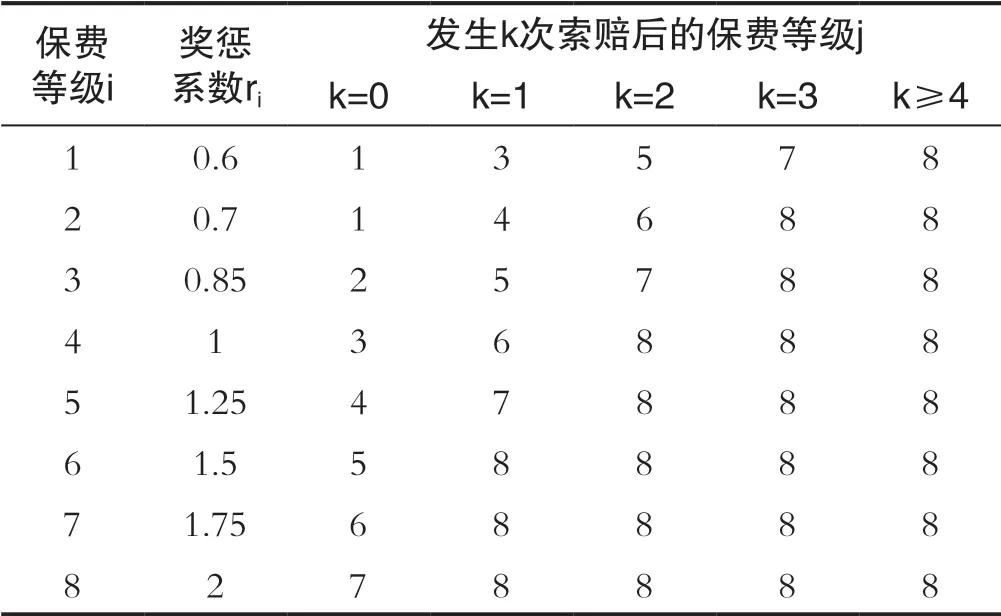
表3 奖惩系统的具体转移规则Tab.3 Specific transition rules for the Bonus-malus system

表3的奖惩系统中，投保人的续期保费等级只与当期的保费等级和索赔次数有关。设Xn表示投保人在第n个保险期内的保费等级，则{Xn，n=0，1，2，...}为一个马氏链，该马氏链的状态空间S为保费等级的集合，即S={1，2，...，8}。由表3可得马氏链对应的转移概率矩阵为

其中pk=P(N=k)，k=0，...，3，qn=P(N≥n)， n=1，...4。由式(6)得p0=0.9323938，p1= 0.0652676，p2=0.0022844，p3=0.0000533，q1=0.0676062，q2=0.0023386，q3=0.0000542，q4=0.0000009。由式(1)和式(7)得稳态概率分布为π=(π1，π2，π3，π4，π5，π6，π7，π8)

由式（6）得P0=e-λ，在区间[λL，λU]=[0.068，0.072]内所以由式(3)得P0的α截集为因为P0=e-λ为非线性函数，所以采用三角近似法计算由式(4)得。同理可得：

用R软件的FuzzyStatProb包可计算模糊稳态概率分布中的α截集上下界的真实值，结合式（1）和式（8）计算得的近似三角模糊数如下

表4的α截集的上下界及误差Tab.4 α-cuts of it's upper and lower bounds and errors

表4的α截集的上下界及误差Tab.4 α-cuts of it's upper and lower bounds and errors

images/BZ_122_1503_2767_1587_2819.pngimages/BZ_122_1191_2761_1284_2817.pngimages/BZ_122_891_2772_974_2822.pngimages/BZ_122_591_2760_676_2812.pngα 0 0.8461048 0.8544213 0.8461048 0.8544213 0 0 0.25 0.8469736 0.8531283 0.8470724 0.8533098 0.012% 0.021%0.5 0.8480278 0.8522171 0.84804 0.8521982 0.001% 0.002%0.75 0.8490109 0.851098 0.8490075 0.8510867 0.0004% 0.001%1 0.8499751 0.8499751 0.8499751 0.8499751 0 0(errα)(errα)

本文从严厉性方面将普通奖惩系统与模糊奖惩系统进行比较。选用相对稳定平均水平(RASL)、对新投保人的隐性惩罚(ECL)、变异系数(CV)指标评价奖惩系统的严厉性，计算公式分别为

令标准保费为1，则保费等级j的保费Pj=rjP，j=1，...，8，稳态平均保费取三角模糊数对应的非模糊数计算模糊稳态平均保费根据表3中的奖惩系数和模糊稳态概率分布的结果计算得保费Pj和非模糊数π'j如表5所示：

根据式（9）、式（10）和式（11）并结合表5中的数值，得奖惩系统严厉性的各指标值如表6所示

表5 稳定状态下各变量的数值Tab.5 Numerical value of each variable in stationary state

表6 奖惩系统严厉性指标值Tab.6 Severity index value of the Bonus-malus system

从表6可以看出，模糊奖惩系统的RASL值略高于普通奖惩系统，说明在模糊奖惩系统达到稳定状态时，投保人所处保费等级分布比普通奖惩系统略均匀；其ECL值略低于普通奖惩系统，说明对新投保人的隐性惩罚略低；其CV值也略低于普通奖惩系统，说明普通奖惩系统较为严厉些。

4 结语

对于奖惩系统的研究，现有文献中，大多数是在具有精确参数的分布下进行的，忽略了模型中的不确定性。考虑到模型中存在的不确定性，本文将索赔次数的分布参数量化成一个三角模糊数来研究奖惩系统。利用模糊转移概率矩阵、三角近似法及FuzzyStatProb包计算得到模糊稳态概率分布将的结果与普通奖惩系统的稳态概率分布π=(πj)对比，发现的1截集πj(1)与πj相等，验证了普通奖惩系统是模糊奖惩系统的一个特例。的0截集给出了稳态概率分布的最大模糊性。

本文从严厉性方面对奖惩系统进行比较，选取RASL、ECL、CV指标对奖惩系统的严厉性进行评价。通过比较各指标值发现普通奖惩系统比模糊奖惩系统略严厉些，对新投保人的隐性惩罚略高。因此，将参数量化成模糊数可以使奖惩系统中包含参数的不确定性，还可以略降低奖惩系统的严厉性。