在数学体验中发展学生的逻辑思维

张健

[摘  要] 在数学领域里面，逻辑主要体现为数学概念以及规律之间的因果关系，推理主要体现为运用逻辑得到新的概念或规律，或者运用概念或规律解决问题. 当前的初中数学教学有着数学学科核心素养培育的任务，因此数学教学更重要的任务就是落实学生的核心素养. 研究表明，让学生进行数学体验可以有效地发展学生的逻辑思维. 当学生身处数学体验时，遇到问题和矛盾是不可避免的，为了解决这些问题或者化解这些矛盾，学生就会自发地寻找逻辑并且建立起逻辑关系. 在这个过程中，概念、判断与推理都是自然的产物，逻辑推理的过程会自然发生，因此逻辑推理能力的培养在某种程度上就是数学体验的必然结果.

[关键词] 初中数学;数学体验;逻辑思维

数学学科核心素养的组成要素之一是逻辑推理，这一界定符合数学教学的传统. 换句话说，在数学教学中一直就有重视逻辑推理的传统，无论是在新的数学知识学习的过程中，还是运用数学知识解决问题的过程中，逻辑推理都发挥着不可替代的作用. 在数学领域里面，逻辑主要体现为数学概念以及规律之间的因果关系，推理主要体现为运用逻辑得到新的概念或规律，或者运用概念或规律解决问题. 在应试的视野下，教师对逻辑推理的重视往往体现在解题上面，而当前的初中数学教学有着数学学科核心素养培育的任务，因此数学教学更重要的任务就是落实学生的核心素养.

通常来说，逻辑推理能力的培养与具体的推理过程有关，而真正要培养的实际上是学生的逻辑思维，当学生具有了逻辑思维后，无论是在新的知识学习中，还是在问题解决的过程中，学生都会自发地进行逻辑推理，并在此过程中进一步提升自己的逻辑思维能力. 当教师的目的在于应试时，培养学生逻辑思维的过程主要是解题的过程，而在培育学生数学学科核心素养时，就需要开辟新的培养逻辑思维能力的途径. 研究表明，让学生進行数学体验可以有效地发展学生的逻辑思维.

数学体验是人们在数学活动中所生成的对数学内容的情感且生成意义的活动. 对于学生的素质形成与素养养成来说，数学体验是核心环节. 有研究表明，学生获得数学体验的教学策略包括：营造开放的课堂教学环境，让学生对学习活动产生强烈体验的内驱力;创设良好的数学问题情境，唤起学生的情感活动，使学生获得发现和提出问题的数学体验;让学生经历“再创造与再发现的过程”，获得科学发现的体验;倡导学生积极主动地参与“数学建模”活动，鼓励学生在数学体验中主动成长. 对于一线教师而言，作为现成的研究成果，通过数学体验来发展学生的逻辑思维时，还需要进行理论上的内化与实践中的探索.

数学体验是逻辑思维培养的有

效途径

从学术定义的角度来看，逻辑思维是借助于概念、判断、推理等思维形式所进行的思考活动，是一种有条件、有步骤、有根据、渐进式的思维方式，是学生数学能力的核心. 其实从这一学术定义来看，逻辑思维是一个非常抽象的概念，如果学生的学习过程也是这么抽象，那么显然不符合初中学生的认知特点. 那么如何让这一过程变得形象呢？最根本的办法还是要让学生完成数学体验.

对体验的理解可以简化为“以身体之，以心悟之”，这是著名的教育家、国家督学、原江苏省教育科学研究所所长成尚荣先生所给出的界定. 笔者认为这一界定非常适合初中数学教师理解“体验”. 相应地，数学体验可以理解为体验的下位概念，当学生心悟的对象是数学学习对象时，那么这样的体验就是数学体验. 体验式学习与传统的讲授式学习，最大的区别之处就在于前者是主动的，而后者是被动的. 当学生主动学习时，他们的学习目标是明确的，而且有可能会寻找到最适合自己的学习方式，在这一过程中必然会有数学体验.

那么为什么说数学体验是逻辑思维培养的有效途径呢？这其中一个至关重要的原因就在于，只要学生主动地获得知识，那么他们就一定会寻找到自洽的逻辑. 如果从哲学的角度来看，这就是说当学生（其实不只是学生，而是所有的人）处于矛盾中时，学生一定会想方设法去解决这一矛盾，从而让自己生活在自洽的逻辑当中. 当学生身处数学体验中时，遇到问题和矛盾是不可避免的，为了解决这些问题或者化解这些矛盾，学生就会自发地寻找逻辑且建立起逻辑关系. 在这个过程中，概念、判断与推理都是自然的产物，逻辑推理的过程会自然发生，因此逻辑推理能力培养的落实在某种程度上就是数学体验的必然结果.

基于逻辑思维培养的数学体验

教学

那么到了具体的教学过程中，如何基于逻辑思维的培养去设计数学体验教学呢？很显然主动权取决于教师. 在具体的教学过程中，教师要发挥主导作用，要利用数学问题、数学辩论、数学活动、数学实践等多种教学手段，为学生提供逻辑思维成长的契机.

例如，在“等腰三角形”的教学中，要让学生理解等腰三角形的性质，就可以设计一个能够让学生进行数学体验的过程. 笔者在教学中重点设计了两个环节：

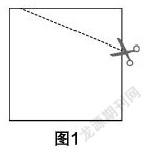
环节1：让学生通过裁剪的方法体验如何得出等腰三角形. 具体的做法是给学生一张长方形的纸片，然后将长方形纸片对折，再通过如图1所示的方式裁剪，将裁剪下来的纸片展开后就得到了一个三角形. 随后让学生观察这个三角形，并借助于几何直观去判断这个三角形的特征.

通常情况下，凭着初中学生的认知能力以及学习经验，往往能够依据直觉判定其是等腰三角形（当然这时学生未必能够说出等腰三角形的概念，但是判定两边相等肯定会出现）. 这时学生判断的主要依据是自己的直觉，但直觉不是逻辑思维能力——事实上，直觉本身也对应着直觉思维，直觉思维是与形象思维和抽象思维并列的思维方式，我们平常所说的逻辑思维实际上是抽象思维的核心组成部分，体现着抽象思维最基本的特征. 不过直觉思维水平有高有低，这里学生通过体验与观察进行直觉判断，是一种水平相对较低的直觉思维，但其是奠定更高水平的逻辑思维能力形成的基础.

环节2：让学生基于操作进行想象，然后梳理出已知条件与求证目标，进而进行逻辑推理. 在上一环节中，学生判定三角形的两边相等是基于对折和剪切过程中形成的三角形的两条边“重合”所得出的结论. 这是数学中的几何直观，也是一种合情推理. 其后，在探究“等腰三角形的性质”而需要进行逻辑推理时，最关键的环节就是根据已知条件去选择推理工具，而这个推理工具就是“三角形全等”的知识.

笔者这里不再赘述具体的证明过程，只是想从逻辑推理的角度进行相关的阐述：其一，根据已知的边与角的关系，选择三角形全等的判定法则进行证明——这是一个在大脑中进行逻辑推理的过程;其二，书写逻辑推理的过程——这是一个运用数学语言展现逻辑推理的过程. 这两者是相辅相成、相互促进的：后者以前者为基础，前者以后者为旨归. 将两者结合起来，追求用精确的数学语言去表征学生严密的逻辑推理过程，是逻辑推理能力能得到充分培养的关键保证.

初中数学体验与逻辑思维培养

的思考

碰到上述例子可以发现，在面向初中学生进行数学教学时，首先要认识到逻辑思维能力的培养是数学学习的一个关键，其次要认识到发展学生的逻辑思维很关键的一点就是为学生创设一个良好的情境，能够让学生在学习的过程中，有明确的、清晰的思维加工对象，思维过程遵循着严密的逻辑，而满足这个条件的重要方式就是体验式学习. 当学生的体验式学习指向数学学科时，这就是真正的数学体验，如此也就证明了数学体验与逻辑思维培养之间确实存在着密切的关系，数学体验可以为学生逻辑思维的发展提供广阔的空间.

总体而言，数学思维能力就是能够用数学的观点去思考问题和解决问题的能力，人们通过大量的实践活动总结归纳出来的数学知识，其本质是数学思维活动最终的结晶. 逻辑思维的过程一定是理性的，因此人们常常将逻辑思维称为理性思维. 逻辑思维是数学思维能力不可缺失的元素，是学科核心素养的重要组成部分. 面向核心素养培育的要求，结合初中学生在数学学习中表现出来的认知方式与特点，数学教师一个重要的任务就是研究教材，将教材中的内容以及其他相关的课程资源组合在一起，去创造一个能够让学生进行充分体验的学习空间. 当学生在这个空间中有了充分的体验后，教师再想方设法将学生形成的感性认识转化为理性认识，并且用数学语言去描述，于是学生就可以顺利地建构起数学知识，同时学生的逻辑思维也能得到充分的发展. 这是一个符合教学规律的认识，在初中数学教学中应当充分理解与运用，以更好地培育学生的数学学科核心素养.

3530501908245