基于压缩感知的混合光谱解析算法
伍 娟 妮
(日日升智能科技发展(山东)有限公司 山东 烟台 264006)
0 引 言
压缩感知(Compressed Sensing)[1-17]是一种近年发展起来的信号处理技术,它利用信号的稀疏性,通过求解欠定线性矩阵方程的解来有效地恢复重建信号。Donoho等科学家于2006首先提出压缩感知的理论并给出了相关的证明。压缩感知理论的出现引起了学术界的极大兴趣,同时工业领域也表现出积极的热情。压缩感知理论研究的不断推进,带动了信息论、信号编码理论和计算机科学发展,也为工程应用领域带来新的技术支撑,进一步促进机器学习、模式识别、图像处理、生物信息处理、医学数据处理和高光谱遥感等领域的发展。
本文概要地介绍了范数、线性系统矩阵方程及常见求解算法[13,19]、稀疏度(Sparsity)[1]、受限等距性(Restricted Isometric Property,RIP)[1]和受限零空间性性质(Restricted Null space Property)[1]等压缩感知问题的基本概念和数学模型。从经典线性代数的角度来看,压缩感知问题可以简化为寻找如下欠定线性矩阵方程组的稀疏解的问题[1]:
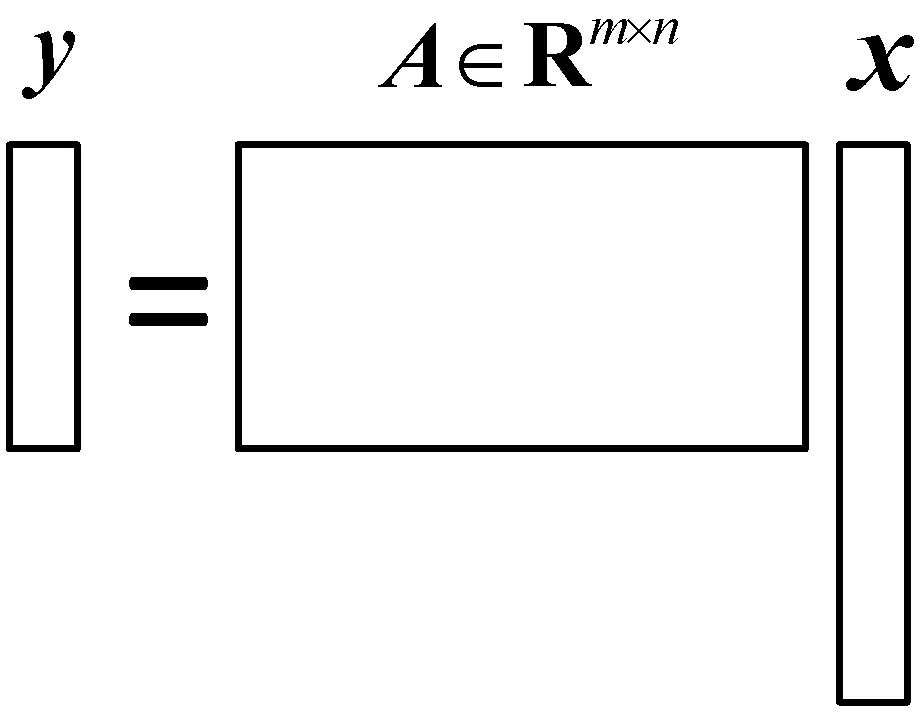
y=Axx∈Rn×1
(1)
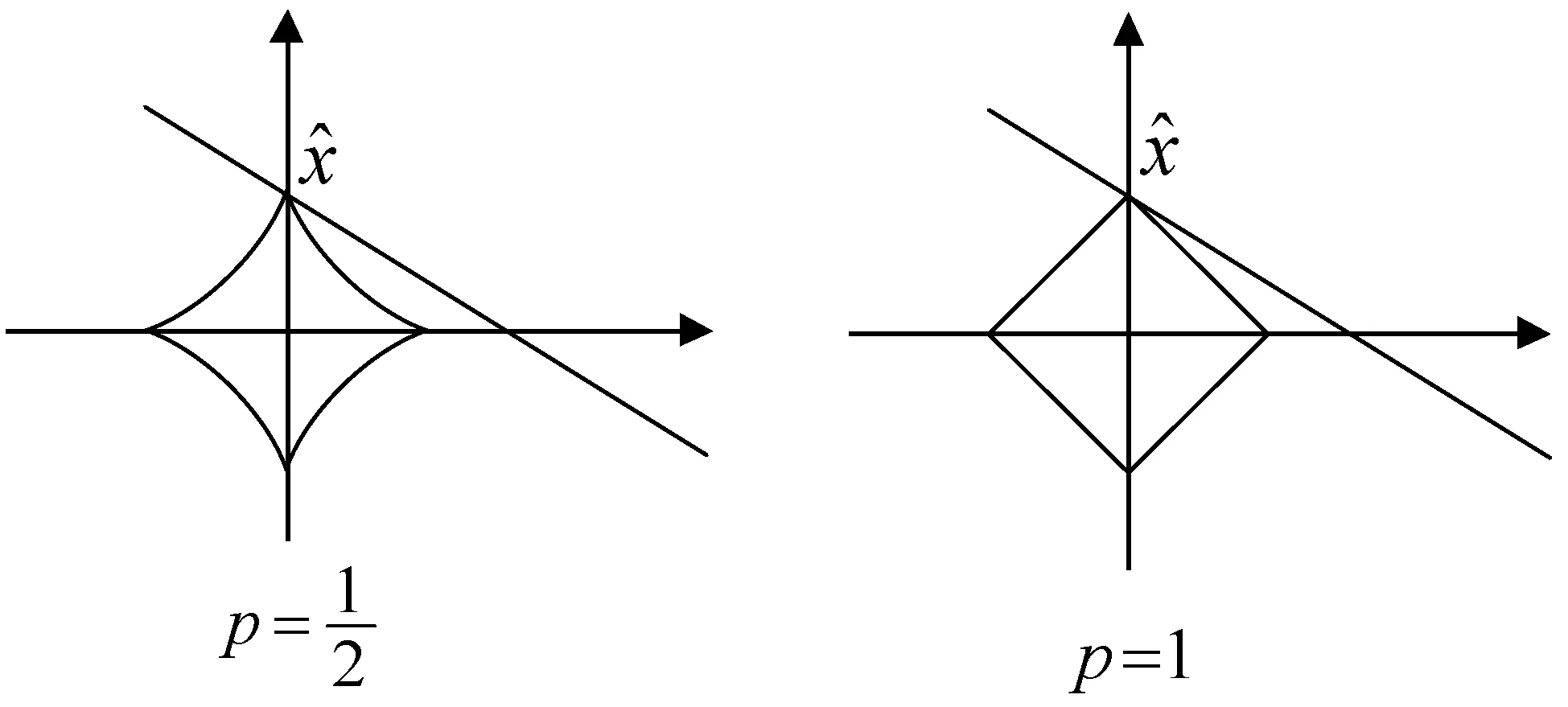
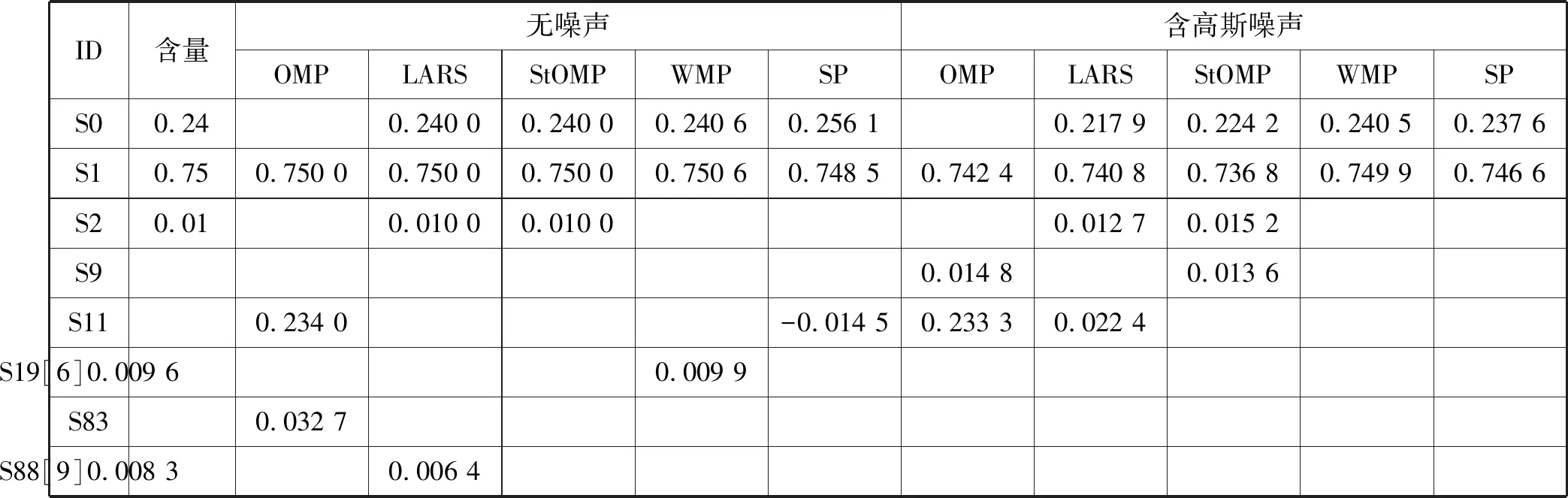
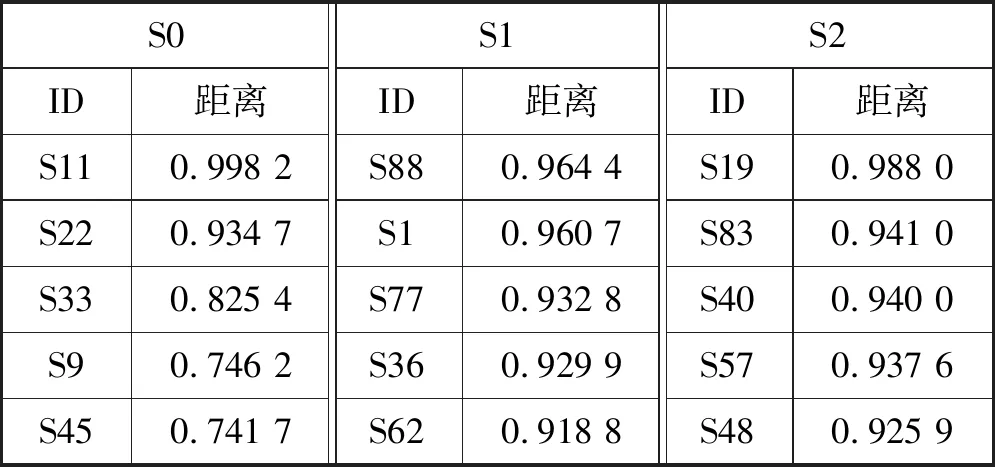
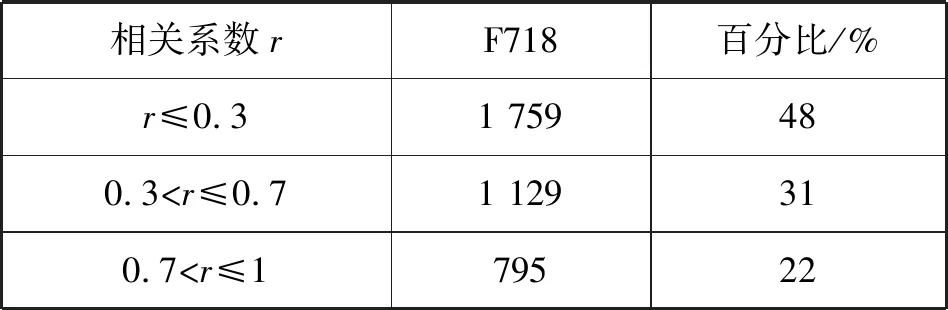
式中:A∈Rm×n(m (2) s.t.y=As 此L0范数优化问题是一个求解组合优化的NP难问题,通常求解很困难。因此,要考虑此问题的L1松弛: (3) s.t.y=As 相关理论证明了当且仅当矩阵A满足受限零空间性质时,L0范数问题与L1范数问题等价[1]。 针对L0范数和L1范数优化问题,本文重点讨论了三种恢复稀疏信号的求解算法。其中正交匹配追踪(Orthogonal Matching Pursuit,OMP)[5]算法是一个近似求解L0问题的贪婪算法,其复杂度低且容易简单。著名的最小角回归(Least Angle Regression,LARS)[5-6]算法求解L1范数问题。分段正交匹配追踪(Stage-wise Orthogonal Matching Pursuit,StOMP)[20]算法与迭代收缩算法存在广泛的相似之处,并且结合了OMP和LARS的优点。 数值实验部分介绍了高光谱图像处理和生物信息学以及化学信息学中的混合光谱模型。混合光谱解析[21-25]是近十年迅速发展的领域,也是高光谱分析领域和生物信息学光谱处理的重点和难点。基于压缩感知的混合光谱分解算法利用已知的光谱库作为基础,代替了端元集合用于高光谱混合像元分解的方法。近年来,随着稀疏表示和压缩感知理论成功地应用于机器学习、图像处理和信号处理领域,研究人员对信号的稀疏性有了更深刻的认识。在高光谱分析领域,Iordache等[26]首次尝试将稀疏性约束加入到高光谱混合像元分解模型中,自此之后,基于稀疏性的高光谱混合像元分解受到国内外学者的高度关注,并成为新的研究热点。 通过两种不同光谱库的具体数值实验,分析了几种稀疏恢复算法在混合光谱解析时的性能和存在的问题,并给出了相应的优化建议。 向量x=(x1,x2,…,xn)的Lp范数定义为: (4) 常见的有L0范数、L1范数、L2范数和无穷(极大)范数: (5) (6) (7) (8) 线性参数估计广泛应用于科学和工程技术领域。线性模型可以表示为如下的线性矩阵方程形式: Ax=y (9) 式中:数据矩阵A∈Rm×n,假设y∈Rm×1,则x∈Rn×1。数据向量y和数据矩阵A的不同,矩阵方程可以有如下四种主要的类型: (1)m=n。即方程个数等于未知量个数,矩阵A和向量y均已知且A非奇异,则方程有唯一解x=A-1y。 (2)m>n。称为超定方程(又称矛盾方程),并且矩阵A和向量y均已知,其中之一或者二者可能存在误差或干扰,此时,方程组没有任何“严格”的解。 (3)m (4) 盲矩阵方程。数据矩阵A未知,向量x未知,仅数据向量y已知。 矩阵方程的高效求解算法一直是数学和计算机算法领域研究的一个核心,本文概述上述矩阵方程的常见求解方法并重点说明欠定矩阵方程的适用条件和常用解法。 1.2.1超定方程m>n 超定矩阵方程中方程个数大于未知量个数,最常用的求解方法是最小二乘法(Least Square,LS)。根据Gauss-Markov定理,如果假设量测误差为高斯正态分布且具有零均等方差,则最小二乘估计量是唯一的一个具有最小方差的线性无偏估计量[19]。 针对矩阵A和向量y的不同情况,分别有普通最小二乘法、数据最小二乘法、Tikhonov正则化方法、总体最小二乘法和约束最小二乘法等多种算法[19]。 最小二乘法的核心思想就是寻找解向量x使得矩阵方程两边的误差平方和最小。矩阵方程Ax=y的普通最小二乘解为: (10) 若矩阵A列满秩,即rank(A)=n,则ATA非奇异,矩阵方程有唯一解: xLS=(ATA)-1ATy (11) 若rank(A) xLS=(ATA)-1ATy (12) 式中:(ATA)-1为ATA的Moor-Penrose逆矩阵。 在工程应用中,数据矩阵A常为秩亏损矩阵,即rank(A) (13) 式中:λ为正则化系数。其解为: xLS=(ATA+λI)-1ATy (14) 在信号处理领域该方法称为松弛法。在机器学习和统计学中,称该L2约束问题为岭回归。 Tikhonov正则化方法实质上是一种改良的最小二乘估计法,通过在矩阵ATA上加入一个惩罚项λI使得矩阵ATA+λI非奇异。它放弃了最小二乘法的无偏性,以损失部分信息、降低精度为代价提高模型的稳健性,获得的回归系数更符合实际、更可靠,对病态数据的拟合要强于最小二乘法。 如果考虑矩阵A和向量y都存在观测误差,并且假设误差是具有相同方差且满足独立同分布的随机变量,则常采用总体最小二乘(Total Least Squares,TLS)法。如果噪声统计相关或具有不同的方差,则考虑使用约束总体最小二乘法,具体内容参阅文献[19]。 1.2.2盲矩阵方程 考虑盲矩阵方程: X=AS (15) 式中:X∈Rm×n为观测矩阵;矩阵A∈Rm×d、S∈Rd×n均未知。若假设A列满秩、S行满秩,则可在已知X的情况下,求解未知矩阵A和S。求解盲矩阵方程的常用方法有:子空间法、非负矩阵分解法和独立成分分析等,具体内容参阅文献[19]及其参考文献。 1.2.3欠定矩阵方程m 欠定矩阵方程中方程的个数小于未知量个数,适用于样本数小于特征数的情况。此时需要考虑三个问题:该方程是否存在稀疏解,该稀疏解是否唯一,如何求解。 压缩感知理论认为:通过信号恢复算法,可以利用信号的稀疏性从比Shannon-Nyquist采样定理所需要的信号少得多的样本中恢复信号。压缩感知理论中的两个最关键的概念就是稀疏度和不相关性。稀疏度要求信号在某个域中是稀疏的,不相关性通过等距特性度量。一般而言,相关性越小,恢复算法的性能越好。 (2) 受限零空间性质。给定矩阵A∈Rm×n,其零空间为: null(A)={x∈Rn|Ax=0} (16) 对于给定的子集S∈{1,2,…,n},若有: null(A)∩C(S)={0} 则称矩阵A∈Rm×n在S上满足受限零空间性质,记为RN(S)。 (3) 受限等距性(Restricted Isometric Property,RIP)。最简单度量方式是让矩阵A中的各列做内积,一个更复杂的不相关概念与受限等距性(RIP)[5,8,27]有关。 对于线性系统Am×nx=y,m>n,若存在常数δk∈(0,1),使得对于任意向量s∈Rk和A的子矩阵Ak∈Rm×k有: (17) 则称矩阵A满足k限定等距性(kRIP)。此时可以通过下面的优化问题近似完美地从y中恢复稀疏信号s,进而恢复出信号x: (18) s.t.y=As 此L0范数最小化问题是一个求解组合优化的NP难问题,通常求解很困难。因此,要考虑此问题的L1松弛: (19) s.t.y=As 当且仅当矩阵Am×n满足受限零空间性质时,L0与L1问题等价[5]。 压缩感知理论同时在信号处理和统计学习领域独立发展,最后得到近似的概念[5]。从经典线性代数的角度来看,压缩感知问题可以简化为寻找如下欠定线性系统的稀疏解的问题: y=Axx∈Rn×1 (20) 式中:A∈Rm×n(m 图1 CS模型 图2 Lp模型 (1) 当0 (2) 当p=1时,Lp球是菱状球,当球与直线Ax=y相交于坐标轴上时得到一个稀疏解。 (3) 当p>1时,Lp球是外凸球,直线Ax=y与外凸球切点一定不在坐标轴上,因而,此时的解是不稀疏解。 欠定稀疏矩阵方程是稀疏表示和压缩感知领域需要求解的问题,其求解方法有贪婪追踪、凸松弛方法、迭代收缩算法、贝叶斯框架和消息传递/置信传播算法[1,17]等。 1) 贪婪算法是稀疏信号处理领域中广泛使用的一种信号复原法算法,此类算法在某些情况下优于凸集选择算法[3]。贪婪算法一般分为贪婪追踪算法和阈值算法。贪婪追踪算法通常以零值为初始值,在每一步迭代中通过最优化方法得到确定的非零值,经过多轮迭代,逐步建立信号的估计。这类方法通常能非常快速地处理较大的数据,但是其理论性能比常规的凸集方法弱。常用的贪婪追踪算法有:匹配追踪(MP)、正交匹配追踪(OMP)、梯度追踪(GP)、共轭梯度追踪(CGP)、分布正交匹配追踪(StOMP)、分布弱梯度追踪(StWGP)和顺序递归匹配追踪(ORMP)等。阈值类贪婪算法在迭代选择非零元素的同时剔除非零元素。此类算法通常简单且运行速度快而且有与凸集算法相当的理论性能,甚至能够用来恢复非稀疏信号,但是计算精度不高。常用的阈值类算法有:迭代硬阈值(IHT)、压缩采样匹配追踪(CoSaMP)、子空间追踪(SP)等。 (2) 考虑到L0与L1问题的受限等价性,在求解欠定矩阵方程的稀疏解时往往使用更容易实现的L1凸松弛算法。Lp优化问题在最优化领域有着广泛而深入的研究和大量的算法,比较常用的最小化L1算法有:Homotropy算法(最小角回归算法LARS)、Chabollet-Pock算法[3],FOCUSS(Focal Undetermined System Solver)算法(又称为迭重加权最小二乘法(Iterative Reweighed Least Squares))[11]等。更深入的研究请参阅相关专著。 4) 稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)的相关理论最早出现在Tipping关于相关向量机(Relevance Vector Machine,RVM)的文献中,之后RVM模型被引入到压缩感知信号恢复中[10]。文献[16]中总结到:SBL算法与广泛使用的L1惩罚算法(如LASSO、BP等)相比优势明显,具体体现在以下几个方面:(1) 在无噪情况下,如果不能满足某些严格的条件,L1惩罚算法的全局最小点并不是真正的最稀疏解,而此时SBL可以更好地得到最稀疏的真实解。(2) 当感知矩阵A的列与列之间相关性很强时,大部分已知算法的性能都比较差,而SBL性能良好。(3) 学者已经证明SBL算法等价于一种迭代加权L1算法,更易获得真正的稀疏解。(4) 当信号不是特别稀疏甚至根本不稀疏时,SBL算法也表现出很好的优势。总之,Bayesian方法对先验知识的使用使得SBL算法可以得到更好的结果。但是相较于其他算法,SBL算法计算速度偏慢。目前该方法已经得到了越来越多的研究和发展。 5) 置信传播(Belief Propagation)[10]是一种在图模型上进行推断的消息传递算法。其主要思想是:对于马尔可夫随机场中的每一个节点,通过消息传播,把该节点的概率分布状态传递给相邻的节点,从而影响相邻节点的概率分布状态,经过一定次数的迭代,每个节点的概率分布将收敛于一个稳态。在求解欠定矩阵方程时,常见的消息传递算法有最小和算法(Min-Sum Algorithm)[3]和近似消息传递(Approximate Message Passing,AMP)算法[3]等。最小和算法可以准确计算LASSO估计的高维极限,而AMP算法允许沿着不同大小的实例序列进行渐近精确分析,特别是在大系统中,AMP算法以指数速度收敛于LASSO最优。 欠定矩阵方程稀疏求解算法的研究仍在不断的发展和更新中,当为某一个具体的应用选择算法时,通常需要权衡不同算法的特性,如:计算速度、存储量、是否易于实现、灵活性、还原效率等因素。本文重点研究以下三个算法: (3) OMP和LARS算法在遇到高维问题时,性能较差。分步正交匹配算法(StOMP)[12]的设计者将OMP与LARS相结合,并且与迭代收缩算法存在广泛的相似之处。 学者已经证明了只要采样矩阵A满足RIP参数,OMP算法就可以使用k个步长精确恢复任意k个稀疏信号[5]。 OMP算法的每一步迭代都基于最佳匹配原则,找出稀疏解的一个非零元素,然后用伪逆修正此非零元素,循环迭代,直到找到所有的非零元素。算法要求已知非零元素的个数即稀疏度k。OMP算法如算法1所示。 算法1OMP算法 输入:给定矩阵A∈Rm×n,向量y∈Rm,误差阈值ε。 输出:向量x∈Rn。 步骤1初始化:令残差r=y,标签集Ω=∅。 步骤2辨识:求矩阵A中与残差向量r最强相关的列,并将其加入标签集Ω。 Ωk=Ωk-1∪{jk} 其中AΩk=[aω1,aω1,…,aω1],ω1∈Ωk 步骤4更新残差:rk=y-AΩkxk。 步骤5更新矩阵A,设第jk列为零或删除此列,因为此列已经被选中。 步骤7输出稀疏向量。 OMP算法时间复杂度为O(kmn),它的变化形式在精度和时间复杂度都有所改进,而且得到了广泛的应用。OMP算法在统计建模中被称为向前逐步回归(Forward Stepwise Regress,FSW)[1],常见的改进还有:纯匹配追踪(Pure MP)[1]、松弛匹配追踪(Relaxed MP)[1]和弱匹配追踪(Weak MP)[1]等。 在统计学习中,L1范数约束问题被称为LASSO(Least Absolute Shrinkage and Selection Operator)。LASSO由斯坦福大学统计系的Hastie等提出[5],是一种不等式约束的普通最小二乘法,具有收缩和选择两种基本功能,常用于回归问题。LASSO方法和岭回归(Ridge Regression,RR)方法一样,都有助于降低过拟合的风险,并且LASSO更易获得“稀疏”解。 最小角回归(LARS)是一种逐步回归的同伦算法,是求解LASSO问题[30-32]的有效算法。LARS算法如算法2所示。 算法2LARS算法 输入:给定矩阵A∈Rm×n,向量y∈Rm。 输出:向量x∈Rn。 步骤1矩阵A归一化,使其样本均值为零,L2范数为1。 步骤2初始化x=0,支撑集S=supp(x)=∅,残差r0=y-Ax=y。 步骤3寻找与残差r具有最大相关性的矩阵A的列ai,即λ0=maxi{ S=S∪{i} 单变量矩阵As 步骤4fork=1 toK=min(m-1,n) (2) 以向量ξ为方向,从xk-1开始,朝着它们的最小二乘解移动系数x,其中As:x(λ)=xk-1+(λk-1-λ)ξ,0≤λ≤λk-1。进一步得到新的残差r(λ)=y-Ax(λ)。 (3) 关注λ=| (4)xk=x(λk)=xk-1+(λk-1-λ)ξ。 (5)rk=y-Axk。 步骤5返回稀疏向量xK。 在LARS算法中,向量集Am×n的角平分线向量(Equiangular vector)μ的定义如下,它与Am×n中的向量的夹角都相等: μ=Equi(A)=A(ATA)-1In (21) 式中:In=(1,1,…,1)n;Equi表示求角平分线向量。 LARS保证当前残差与已经入选的变量之间的相关系数相等,选择当前残差在已经入选的变量构成的子空间上的投影为求解路径,继续搜索,寻找新的满足条件的变量,加入之前的子空间,并更新寻找路径。 LARS算法利用LASSO系数路径是分段线性的事实,通常情况下,LARS算法更加准确,计算复杂度更低,并且对于低维问题能够得到一个更好的解。一般情况下,LARS的步骤等于A的维度,因此在高维问题上,其计算代价更高。 与OMP算法相比,StOMP的每个阶段都有多个系数可以进入模型,而OMP的每个阶段只能选择一个系数。对于每步选择多个元素的StOMP而言,迭代多次(建议10次)可以得到近似线性系统y≈Ax所需的稀疏解。StOMP算法如算法3所示。 算法3StOMP算法 输入:给定矩阵A∈Rm×n,向量y∈Rm,误差阈值ε。 输出:向量x∈Rn。 步骤1初始化x0=0,支撑集S=supp(x)=∅,残差r0=y-Ax0=y。 步骤2残差向后投影: 计算ek=AT(y-Axk-1)=ATrk-1 步骤3阈值选择: 如果选择阈值使得|Jk|=1,即每次更新一项,则得到OMP。 考虑一般情况,每次迭代可更新多个项。 步骤4支撑集更新:Sk=Sk-1∪Jk。 步骤5带约束最小二乘:给定支撑集,并假设|Sk| 式中:P∈Rn×|Sk|是一个选择算子,从向量x中选择允许为非零项的|Sk|的个数。 步骤6更新残差:rk=y-Axk。 步骤7循环执行步骤2到步骤6,直到停止迭代。 步骤8返回稀疏向量x。 本文所述实验用到的算法程序为自编写软件,运行环境:Windows操作系统;开发环境:Visual Studio S2015;算法:C++语言和Armadillo库。 光谱分析法是根据物质的光谱来鉴别物质及确定其化学组成和相对含量的方法。在高光谱图像(Hyperspectral image)[33-41]分析领域,混合光谱常称为混合像元,纯物质称为“端元”(Endmember),各个端元所占的比例称作“丰度”(Abundance)。高光谱解混(或称混合光谱分解)(Hyperspectral Unmixing,HU)或称光谱混合分析(Spectral Mixture Analysis)的目的就是分析出混合光谱内包含的不同纯物质的光谱信号及其含量。高光谱混合模型主要有线性和非线性两种。线性模型(Linear Spectral Mixing Model,LSMM)假设单一光子仅能影响一类地物并将反射结果线性累积到像元光谱中。在生物信息学和化学信息学中[42],如何有效地分析复杂多组分体系中的组分及其含量一直是分析化学研究的难点。自然界的物质往往以混合物的形式存在,比如中草药成分中的有效和有毒成分分析、痕量物质的检测等。在生物信息学和化学信息学的光谱分析中存在类似的线性光谱混合模型,根据多组分体系的朗伯-比尔定律和加和定律,混合物的光谱可以表示为:y=Ax+e,其中:y为目标光谱向量;x为光谱浓度向量;A为已知光谱样本;e为残差。混合光谱解析也就是在已知光谱库中找到某一光谱或者光谱组合可以最好地逼近目标光谱。 本文描述如下两个数据源不同的实验:实验一中的数据源光谱矩阵A20×3 683中的各个数据之间的距离比较分散,而实验二中的数据源矩阵A91×1 867中包含非常近似的数据。因为MDS算法能够保证原始空间中的距离在低维空间中得以保持,数据源均采用多维尺度分析(Multidimensional Scaling,MDS)[43-44]算法进行降维可视化以帮助分析高维数据之间的关系。在本实验中,MDS算法选用光谱分析中常用的Cosine距离作为度量标准。 4.3.1实验一 量测矩阵(谱库)A20×3 683由20个长度为3 683的红外纯物质光谱构成,测试用混合光谱分别有带噪声和不带噪声两个目标光谱,均通过模拟计算得到,其拟合公式为: T=0.24S0+0.69S1+0.07S2(+Gaussian) 式中:S0、S1、S2表示光谱;Gaussian表示高斯噪音。 图3、图4和图5分别为量测矩阵(谱库)A20×3 683的MDS降维可视化、混合物光谱、纯物质光谱。 图4 混合物光谱(0.24S0+0.75S1+0.01S2+Gaussian) 图5 纯物质光谱1(从上到下依次为S0、S1、S2) OMP、LARS和StOMP三个算法的计算结果如表1所示。可以看出,算法OMP、LARS和StOMP在此测试集上均能很好地计算混合物所含纯物质及其含量。 表1 混合光谱分解1 4.3.2实验二 量测矩阵(谱库)A91×1 867由91个长度为1 867的红外纯物质光谱构成,测试用混合光谱分别有带噪声和不带噪声两个目标光谱,均通过模拟计算得到,其拟合公式为:T=0.24S0+0.69S1+0.07S2(+Gaussian)。图6、图7和图8分别为矩阵量测矩阵(谱库)A91×1 867的MDS降维可视化、混合物光谱纯物质光谱,表2为本文算法的计算结果。 图6 量测矩阵(谱库)A91×1 867的MDS降维 图7 混合物光谱(0.24S0+0.75S1+0.01S2+Gaussian) 图8 纯物质光谱2(从上到下依次为S0、S1、S2) 表2 混合光谱分解2 此实验数据表明,算法OMP、LARS和StOMP在此测试集上均存在误差,因此引入弱匹配追踪(Weak Matching Pursuit,WMP)[1]和子空间追踪(Subspace Pursuit,SP)[1]进行对比研究。为了分析算法的计算精度,表3给出了在数据源中与S0、S1和S2三种物质的Cosine距离最小的5个光谱。 表3 Cosine距离 当混合光谱不包含噪声时,LARS和StOMP在此测试集上能很好地计算混合物所含纯物质及其含量。但是OMP算法得到的结果有偏差,其中S1的含量最大,得到的结果正确,但是从含量数据分析,OMP算法错误地把S0和S11混淆,因为这两个光谱的Cosine距离等于0.998 2;把S2和S83混淆,因为这两个光谱的Cosine距离等于0.941 0。 当混合光谱含有均值为零、方差为1的高斯噪声时,对于含量最大的S1,五个算法能得到几乎都正确的结果,但是WMP的计算精度最高。对于其他混淆的光谱S2与S19,其Cosine距离为0.998 0。 4.3.3结果分析 总体上来说,对于含量最大的光谱S1(含量0.75),在含噪声和无噪声模型中,均能得到比较满意的结果。对于含量为0.24的光谱S0,OMP算法容易把它与其相近的光谱混淆。但是对于含量只有0.01的光谱S3,因为数据源中有与其非常相似的光谱,所以只有LARS和StOMP在不含噪声的模型中给出了准确的结果,在其他算法和模型中,该物质均没有被正确识别。 混合物光谱解析的一个难点在于含噪声系统中精确计算痕量物质的性质及其含量,可能的优化方法有: (1) 谱库筛选:根据目标光谱筛选构成矩阵A的谱库,在其满足算法成立的数学条件情况下,尽可能少地包含相似数据。比较图3和图6,实验一的数据源中的各个光谱的距离较远(图3),而实验二的数据源中有些光谱的距离非常近(图6)。 (2) 特征选择:从n个维度中选择出能代表整体特性的k(k 以实验一为例,数据矩阵A20×3 683的第718号属性是一个特征峰位置,此特征峰与其他属性的Pearson相关系数如表4所示,数据显示,其中有22%的属性与该属性的相关系数大于0.7。 表4 第718号属性与其他属相之间的相关系数 需要说明的是,虽然相关系数接近于1的程度与数据维数n相关。当n较小时,相关系数的波动比较大,仅仅根据相关系数判定变量x与y之间的线性关系时误差较大。但是在光谱数据中,特征数n一般都比较大,简单起见,本文采用相关系数作为度量标准来说明特征之间的线性相关性。 (3) 滤波:采用合适的滤波技术和算法,尽可能地提高混合光谱的信噪比。 (4) 恢复算法的选择和优化:根据具体问题选择合适的算法,提高计算精度和性能。 本文未分析各个算法的时间复杂度,特别是面对大数据量时,时间复杂度会是一个衡量算法性能的关键因素。除了发展速度更快的算法外,并行计算、GPU、通过小波变化压缩数据等都是提高算法计算速度的有效方法。 压缩感知自创始以来受到了学术界和工业界的广泛关注,它利用了信号的稀疏特性,通过求解欠定线性系统的稀疏解来有效地恢复重建信号,改变了传统信号处理中数据采集然后压缩(特征提取)再传输(处理)的模式,在信息理论、信号/图像处理、医学成像、模式识别、生物信息、光学/雷达成像和无线通信等诸多领域有着重要的理论研究和应用价值。 压缩感知相关的理论比较复杂,本文从欠定线性矩阵方程开始,介绍了压缩感知的基础知识。最后,通过两种不同光谱库的具体数值实验,重点讨论了OMP、LARS和StOMP稀疏恢复算法在混合光谱解析时的性能和存在的问题,并给出相应的优化建议。通常认为求解压缩感知问题的方法有贪婪追踪、凸松弛方法、迭代收缩算法、贝叶斯框架、消息传递/置信传播(Belief Propagation)算法等。通过压缩感知算法精确恢复信号的方法基于光谱库完备的假设,随着压缩感知和稀疏表示理论的蓬勃发展,学者们对稀疏性有了更为深刻的认识,稀疏化建模在光谱学等一些高维数据分析领域中都有着广阔的应用前景和深入的研究空间。1 基础概念
1.1 向量范数

1.2 线性模型
2 压缩感知
2.1 概 述
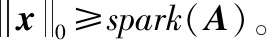
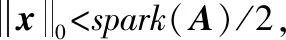
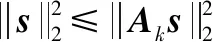
2.2 数学模型
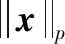
3 算 法

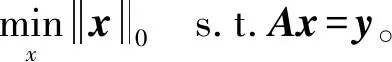
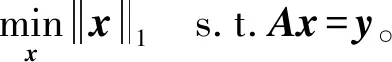
3.1 OMP算法
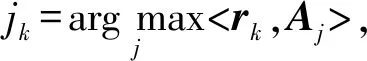
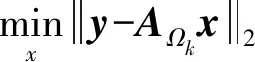
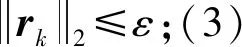
3.2 LARS算法
3.3 StOMP算法
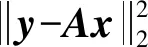
4 实 验
4.1 实验环境
4.2 光谱混合模型
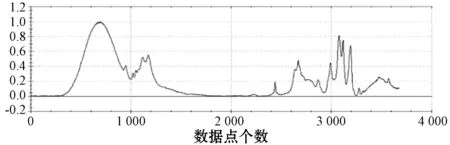
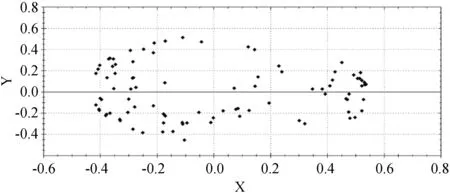
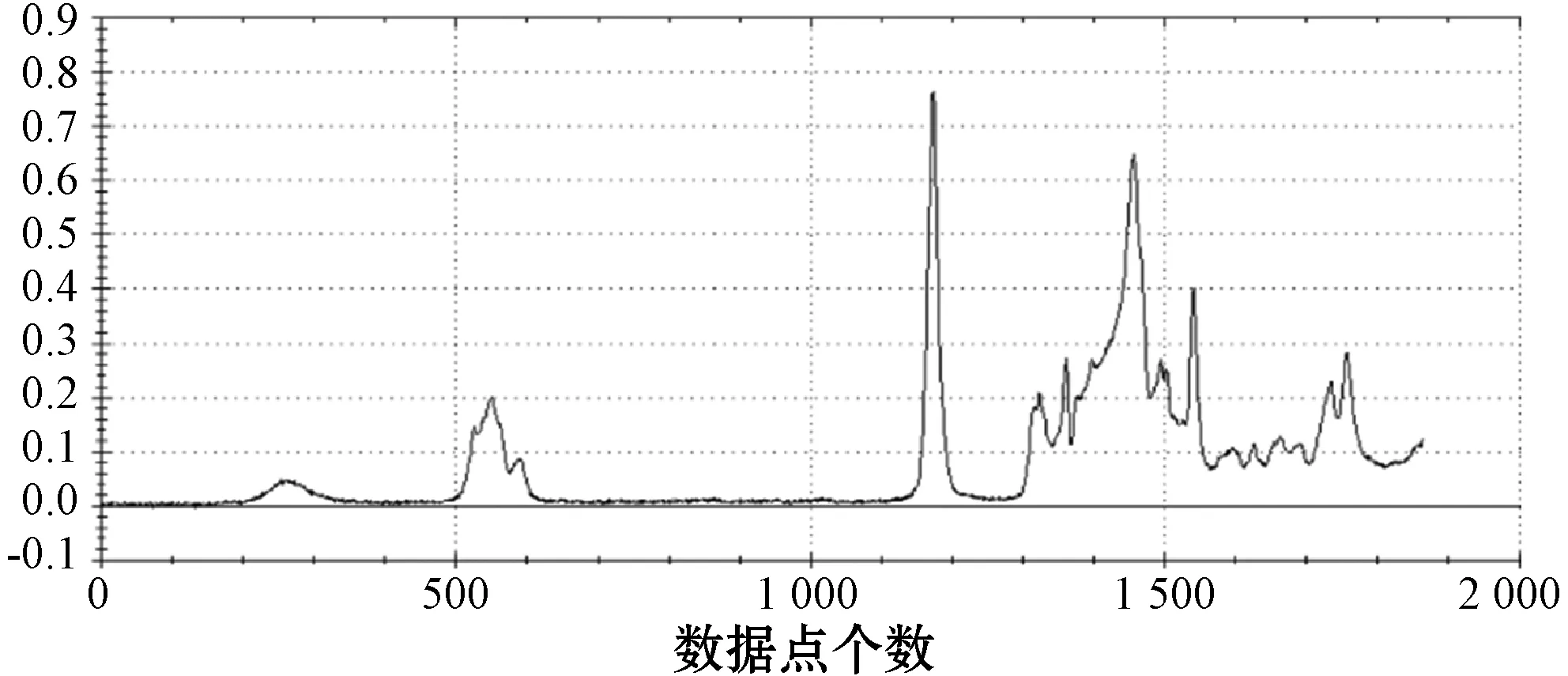
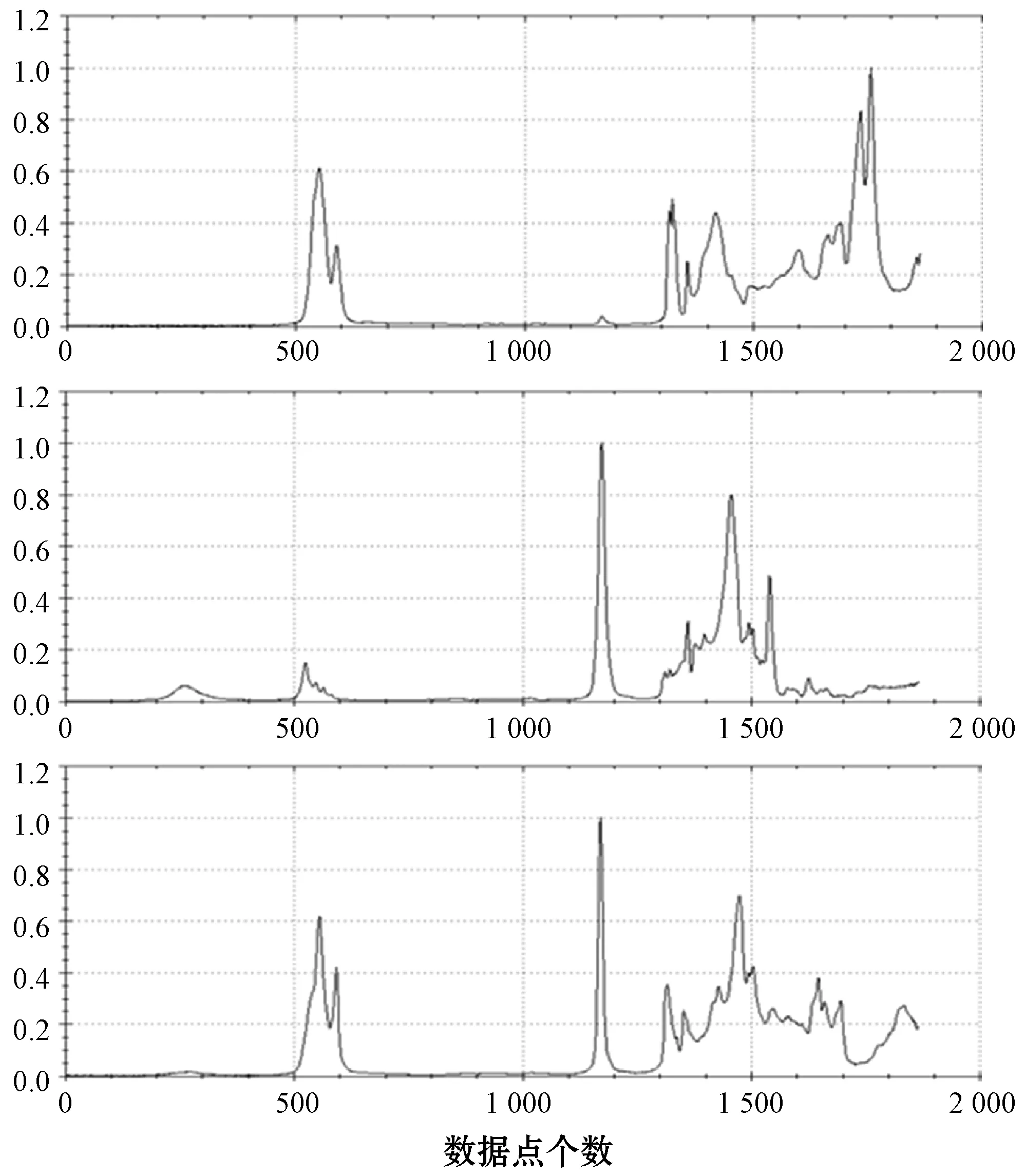
4.3 实验设置与结果分析


5 结 语

