轮式机器人分数阶滑模内模速度控制器设计
王 鑫 刘怡明 王明明* 孙晓云
1(石家庄铁道大学电气与电子工程学院 河北 石家庄 050043)2(苏州大学机电工程学院 江苏 苏州 215137)
0 引 言
轮式机器人具有速度快、效率高的优点,广泛应用于矿山检测、市政检测等领域[1-2]。针对轮式机器人无刷直流电机(Brushless Direct Current Motor,BLDCM)驱动系统,传统PID控制策略,速度响应慢、抗干扰能力差、过度依赖精确的数学模型,文献[3-4]将模糊控制与PID结合,虽然不需要精确的数学模型,但隶属度函数的选取需要大量的经验,难达到最好的效果。文献[5-6]将滑模控制应用于BLDCM调速系统,使系统参数变化时不受影响,在内外扰动下系统具有良好的鲁棒性,但滑模控制易出现系统抖振。文献[7]采用指数趋近律滑模算法对BLDCM进行调速控制,但在原点处存在带状高频抖动。文献[8]将神经网络与滑模控制结合,抑制了系统抖振,但未考虑调节时间。文献[9]将分数阶滑模控制应用于消除永磁同步电机系统抖振,同时使系统具有较少的响应时间。文献[10]将内模控制应用于消除内环干扰,使整个系统具有干扰抑制特性。
本文在深入研究轮式机器人运动方式与BLDCM调速的基础上,结合分数阶滑模控制与内模控制提出一种轮式机器人分数阶滑模内模调速新方法。为了验证算法的有效性,通过搭建MATLAB/Simulink与Carsim 联合仿真平台,在不同路面扰动的情况下进行启动加速与速度突变的仿真实验。实验结果表明,分数阶滑模内模速度控制器可以有效地降低速度响应时间,消除干扰,提高系统的鲁棒性。
1 轮式机器人模型建立
1.1 Carsim简介
Carsim是用于车辆动力学的专用仿真软件,可以模拟道路和空气动力输入的响应,并且主要用于预测和模拟总体车辆操纵稳定性。本文借助Carsim的路面输入响应,进行轮式机器人在不同路面下的仿真实验,用于轮式机器人速度控制器的开发。
1.2 BLDCM数学模型
针对BLDCM为两相导通星形三相六状态的情形,在理想状态下,三相绕组的电压平衡方程式为:
(1)
式中:Ua、Ub、Uc为三相绕组的相电压;ea、eb、ec为三相绕组的反电动势;ia、ib、ic为三相绕组的相电流;M为各相绕组之间的互感;r为各相绕组的电阻;L为各相绕组的自感。BLDCM定子绕组产生的电磁转矩可表示为:
(2)
式中:Te为电磁转矩;ω为电机机械角速度。运动方程为:
(3)
式中:TL为负载转矩;J为电机转动惯量;B为阻尼系数。
1.3 轮式机器人差速运动模型建立
为了轮式机器人更加灵活、转弯半径更小、适应更多的路况,建立前后四轮差速控制模型,将轮式机器人抽象成前、后两个转向模型进行分析,前后轮差速转向模型的转矩分配状态直接由转向模型进行确立。模型中内外轮的转矩比为:
(4)
式中:W为轮距;H为轮式机器人质心到地面的高度;w为电机机械角速度;V为轮式机器人速度;g为重心加速度;θ为转向角度。在转向过程中,内外侧轮的转矩差为ΔTp:
(5)
轮式机器人内外侧轮在转向过程中所需的实际转矩分别为:
Tin=Te-ΔTp
(6)
Tout=Te+ΔTp
(7)
根据轮式机器人运动方式,利用MATLAB/Simulink与Carsim建立四轮差速运动模型,通过Simulink和Carsim的接口设置来完成轮式检测机器人的驱动系统与整车模型之间的信号传递, 实现将电机转矩直接加载到车轮上。每一个车轮由一个BLDCM进行控制。Carsim系统输入输出如表1所示。
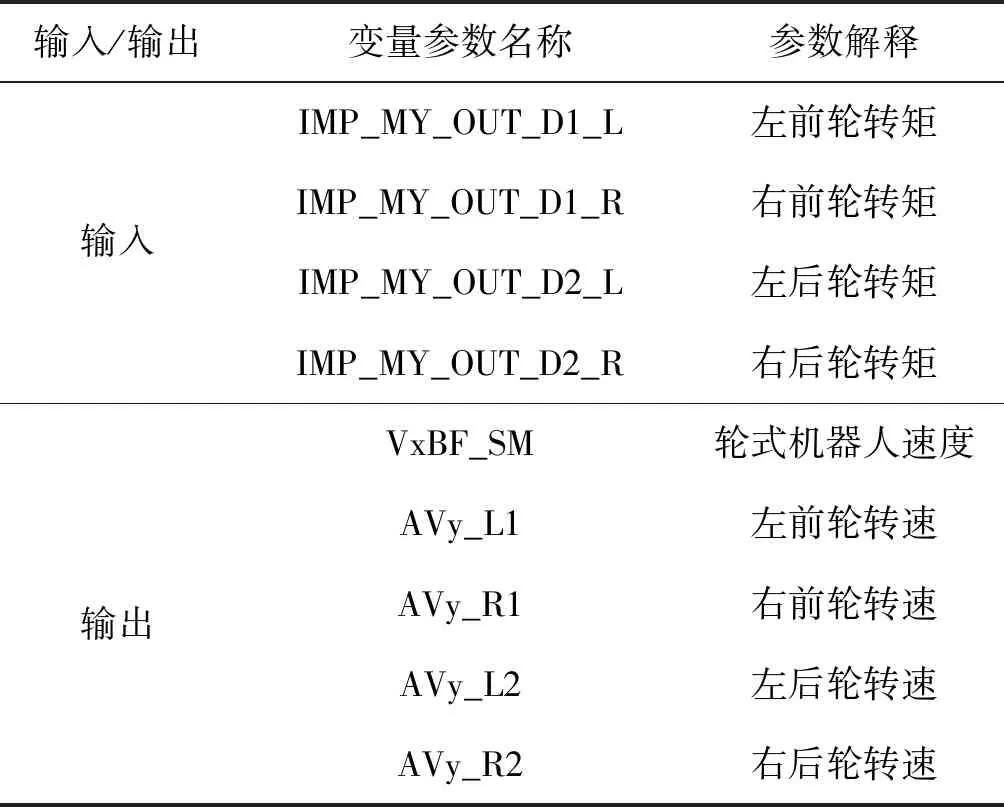
表1 Carsim系统输入输出
Simulink和Carsim控制结构如图1所示。
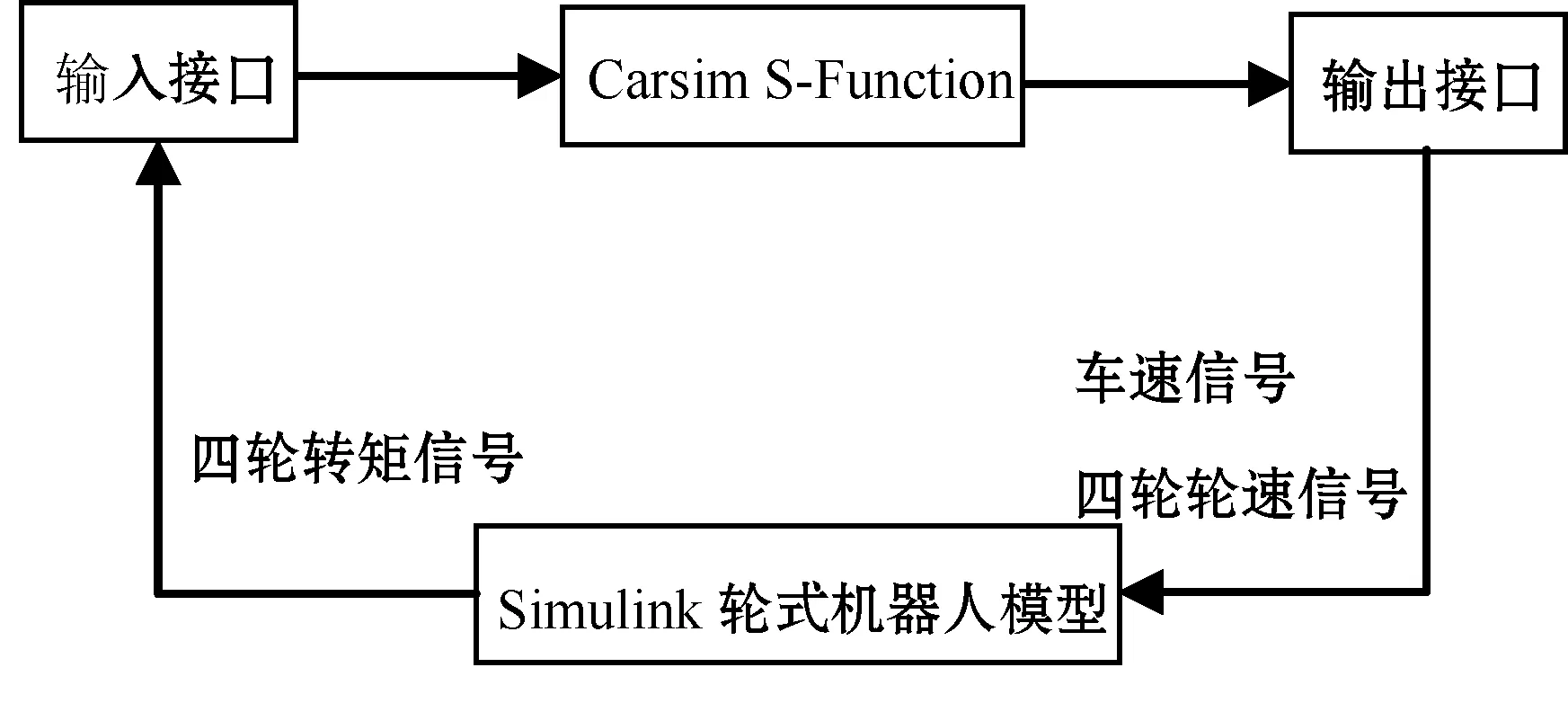
图1 控制结构
2 轮式机器人调速系统设计
2.1 分数阶滑模控制简介
分数阶滑模控制是由分数阶算子与滑模控制结合而成的。一般将分数阶微积分的基本操作算子定义为aDta,具体形式为:
(8)
式中:a为阶次,Re(a)为其实部;α是操作算子的下限,t为上限;τ为积分的导数。
随着对分数阶的认知与分析,常用的为Grünwald-Letnikov(GL型)、Caputo(C型)和Riemann-Liouville(RL型)。
其中RL型分数阶微积分定义为:
(9)
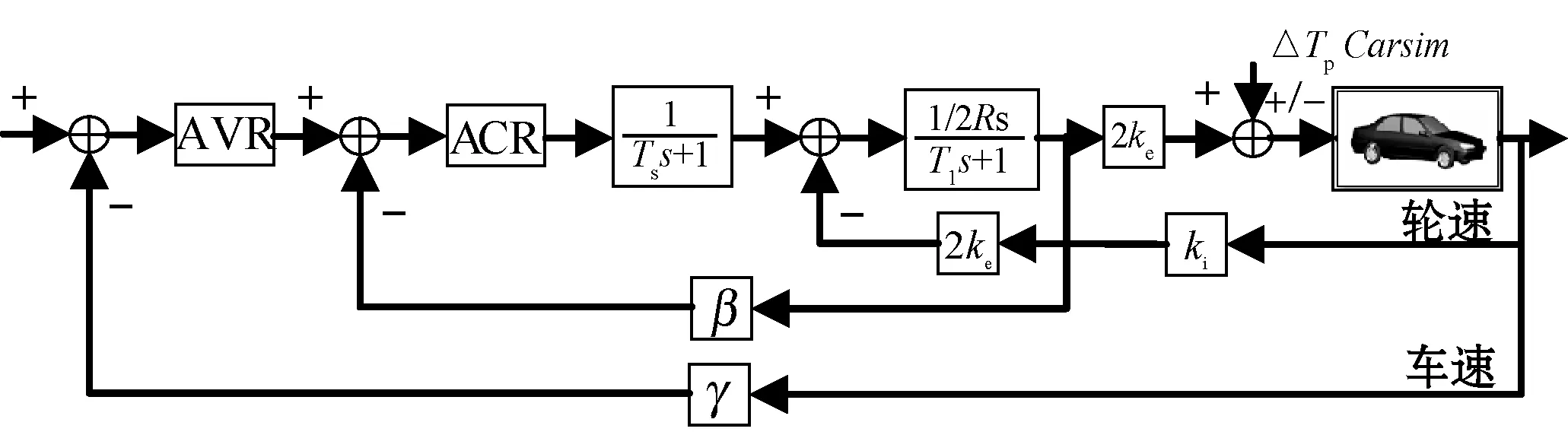
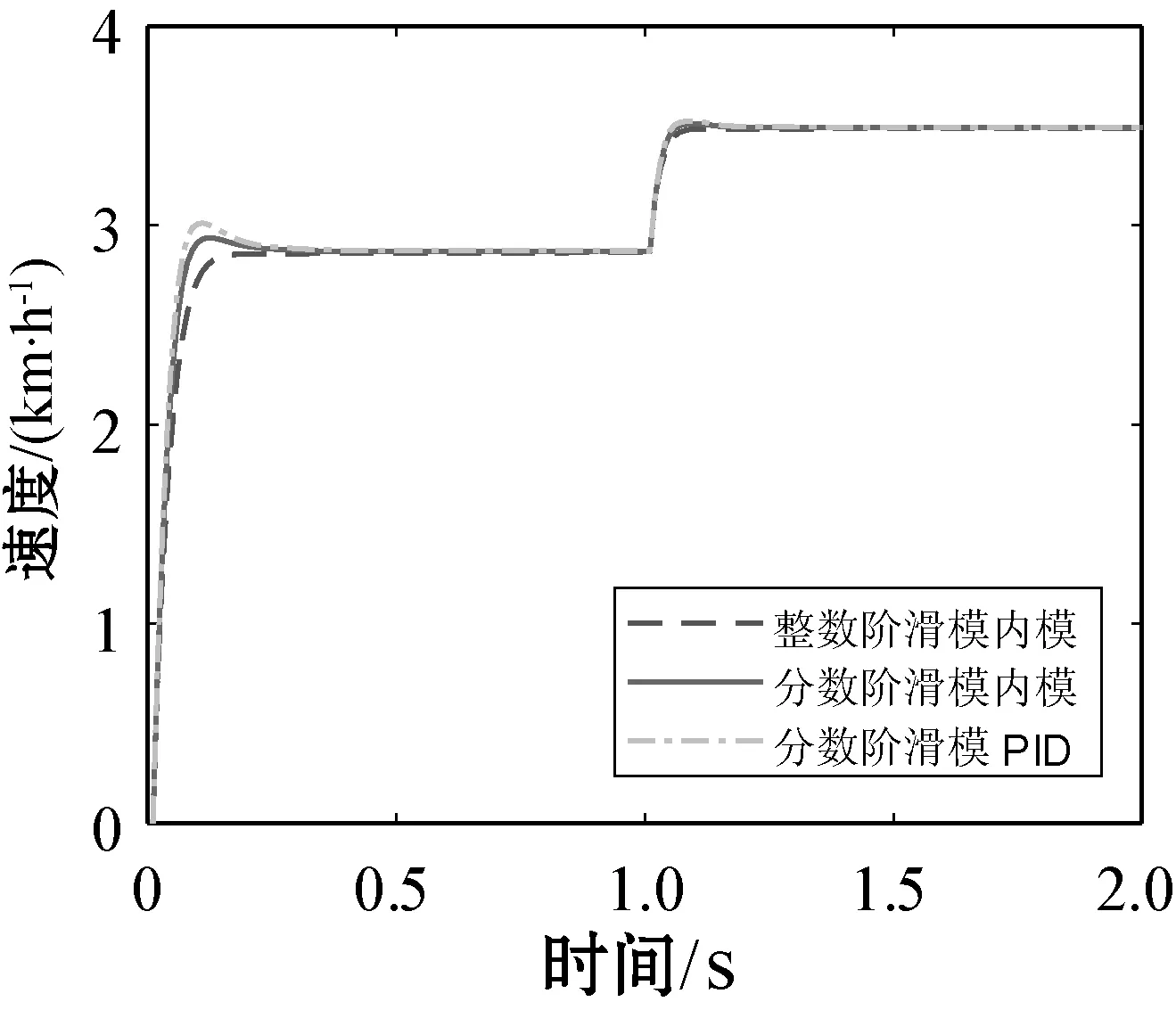
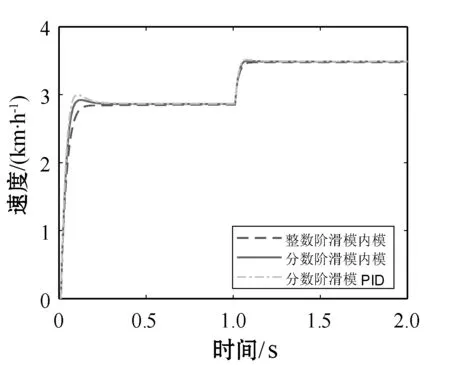
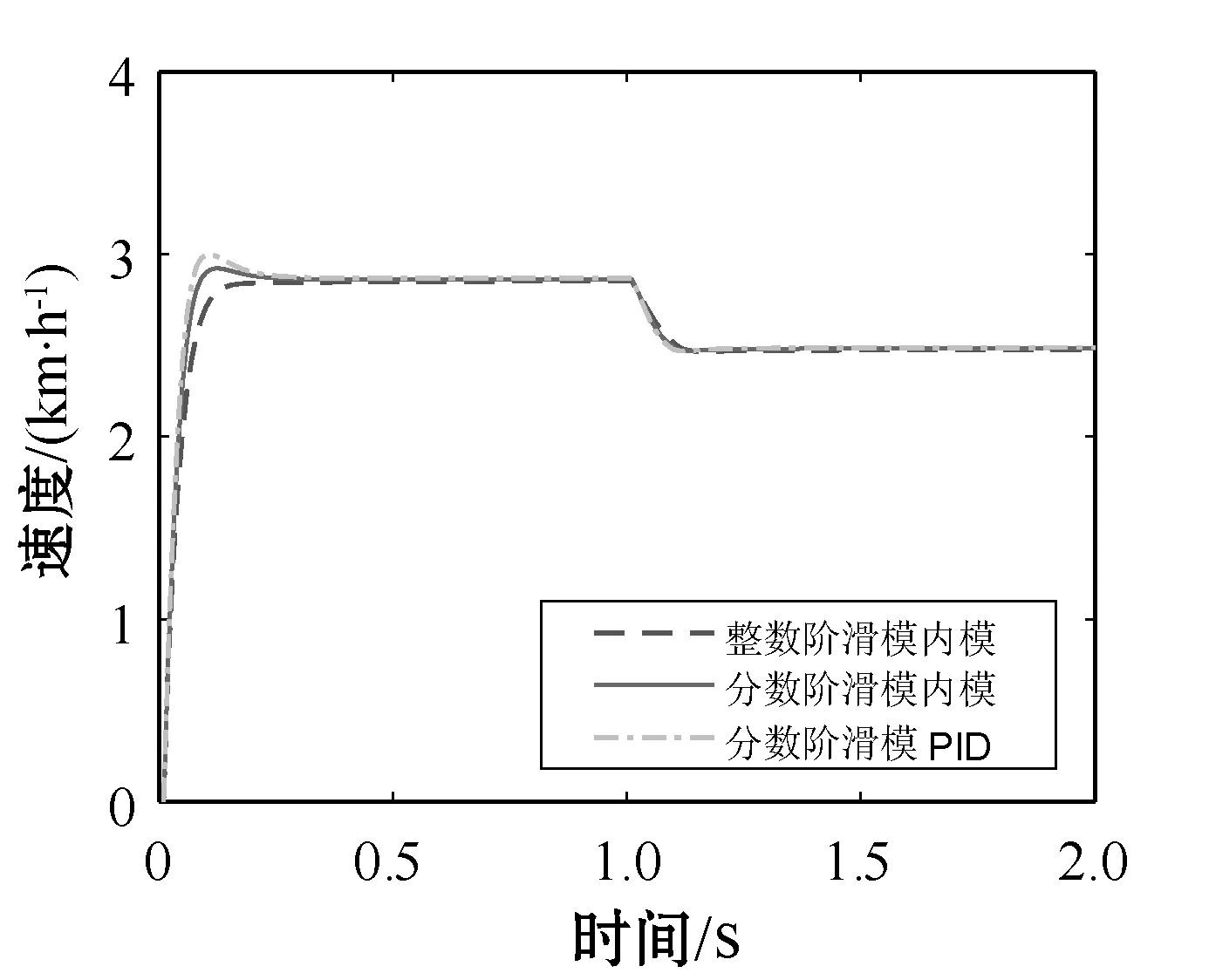
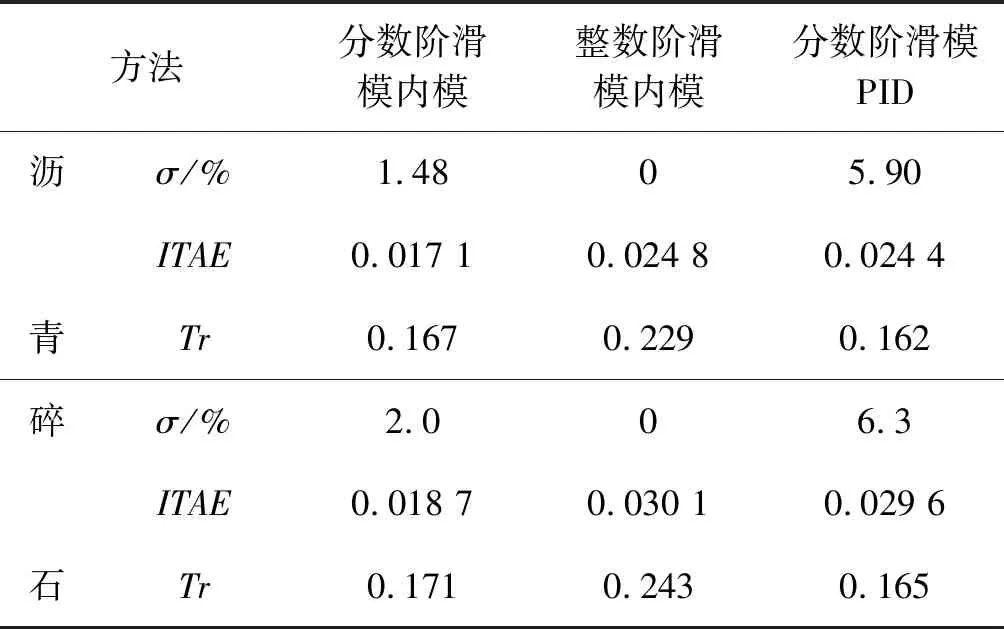
式中:m∈N;a满足m-1 RL函数的分数阶积分的Laplace变换为: L[αDt-af(t)]=s-aL[f(t)]=s-aF(s) (10) 利用BLDCM数学模型,忽略粘滞摩擦系数的影响,改进式(3)为: (11) 则BLDCM的状态方程为: (12) 式中: (13) (14) 电流i为输出,转速偏差为输入。 取分数阶积分滑模面为: (15) 式中:c为滑模面增益,且c>0。指数趋近律为: (16) 式中:ε>0;k>0。 则分数阶滑模控制的控制结果为: (17) 分数阶滑模控制的结果,使得输出的电流变为分数阶积分,降低了电流环输入的波动,提高了系统鲁棒性。 采用李雅普诺夫稳定性来分析分数阶滑模控制的有效性,设李雅普诺夫函数为: (18) 对其求导得: s×[-εsgn(s)-ks]= -εs·sgn(s)-ks2 (19) 加入干扰项后,有新的状态方程: (20) 为了满足李雅普诺夫函数,有: (21) 结合内模控制器原理可知,内模控制系统输出为: (22) 式中:R(s)为系统输入;Y(s)为系统输出;CIMC(s)为内模控制器;G(s)为实际被控对象;GM(s)为被对象数学模型;D(s)为扰动。 根据BLDCM结构,电流环结构如图2所示。 图2 电流环结构 假定被控对象与模型匹配,则: (23) 根据内模控制器的设计原则,将模型GM(s)分解成: GM(s)=GM+(s)GM-(s) (24) 式中:GM-(s)具有最小相位特征,而GM+(s)则为模型非最小相位部分,包含时滞环节和右半平面零点。 为保证内模控制器的可实现性,提高系统的稳定性和鲁棒性,引入低通滤波器f(s),将电流内环看成一阶惯性系统,则电流内模控制器CIMC(s)为: (25) (26) 则电流环内模控制器传递函数为: (27) 存在λi使得: Y(s)=R(s) (28) 从式(27)与式(28)容易看出,电流环内模控制器只需调节一个参数λi,使得控制参数调节更加简便,并且可以消除负载变化带来的干扰D(s),从而提高系统的鲁棒性。 为了验证分数阶滑模内模调速方法的优越性,利用MATLAB/Simulink与Carsim软件进行仿真实验,并与整数阶滑模内模控制、分数阶滑模PID控制进行对比分析。 以轮式机器人速度作为外环,根据实际速度与设定的速度偏差进行控制,使轮式机器人速度快速地跟随给定速度变化,电流环作为内环,速度环的控制输出作为电流控制的输入,紧紧跟随速度环的变化进行控制,最后结合Carsim反馈的轮式机器人轮速信息,完成整个系统的控制。速度环和电流环分别由控制器AVR和ACR控制,速度控制器AVR使用分数阶滑模控制器;电流控制器ACR为内模控制器。轮式机器人调速系统(单个轮子)动态结构如图3所示。 图3 轮式机器人调速系统(单个轮子)结构 设定轮式机器人车长:820 mm;车宽:695 mm;车高:356 mm;车重:65 kg;车轮半径:150 mm;轮距:602 mm;轴距:504 mm;电机额定功率5 kW;电阻(Rs):0.125 Ω;电感(T1):3.75 mH;反电动势(ke):0.25 V·(r·min)-1;电流反馈系数(ki):36;PWM延迟系数(Ts):0.4。 在Carsim中,根据不同的地面滚动摩擦系数与滑动摩擦系数,选取沥青与碎石两种不同的路面扰动进行仿真实验。设置启动速度为2.88 km/h,突然加速实验在1 s时速度由2.88 km/h变为3.50 km/h;突然减速实验在1 s时速度由2.88 km/h变为2.50 km/h。 根据所建模型,首先在沥青地面的情况下进行仿真实验。沥青地面突然加速过程如图4所示。 图4 沥青地面突然加速过程 沥青地面突然减速过程如图5所示。 图5 沥青地面突然减速过程 根据参数设置对碎石路面进行仿真实验,碎石地面突然加速过程如图6所示。 图6 碎石路面启程突然加速过程 碎石地面突然减速过程如图7所示。 图7 碎石地面突然加速过程 由图4-图7可知,分数阶滑模内模在轮式机器人速度变化过程中,速度快速跟随到设定值且基本上无超调。为了进一步证明本文算法的有效性,选取超调量σ、上升时间Tr与时间乘绝对误差积分准则ITAE进行评估,对图4、图6前1 s数据进行处理,数据处理结果如表2所示。 表2 数据处理结果 由表2数据分析可知,在不同的地面干扰情况下,分数阶滑模内模控制较分数阶滑模PID控制在保持快速性的同时降低了系统超调;分数阶滑模内模控制速度响应优于整数阶滑模内模控制,且在保持快速性的同时只存在少量的超调,证明控制系统具有良好的动态响应;从ITAE指标也可以看出,分数阶滑模内模控制瞬态响应的振荡性小。 综上所述,分数阶滑模内模速度控制器对于外部干扰具有较强的抗干扰能力、响应速度快、响应速度曲线波动小,能够快速达到设定速度,并以设定速度平稳运行。 在不同路面的扰动下,为了提高轮式机器人的响应速度,降低外部扰动对调速系统的影响,改善系统抖振。本文在轮式机器人无刷直流电机调速系统的基础上,结合分数阶滑模控制与内模控制策略,提出一种调速控制新方法。通过搭建MATLAB/Simulink与Carsim联合仿真平台,与分数阶滑模PID控制和整数阶滑模内模控制进行对比实验,实验结果表明,分数阶滑模内模控制器能有效降低速度响应时间,减少扰动对速度控制的影响,消除系统抖振,提高系统的鲁棒性,可应用于以速度调控为主导的控制系统。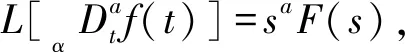
2.2 速度环分数阶滑模控制
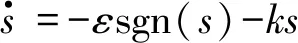
2.3 分数阶滑模稳定性分析
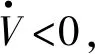
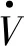
2.4 电流环内模控制
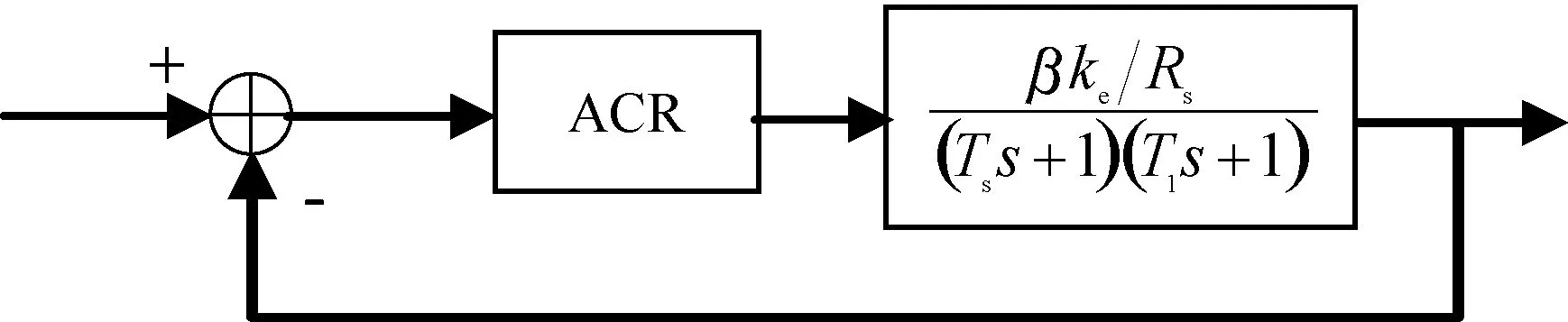
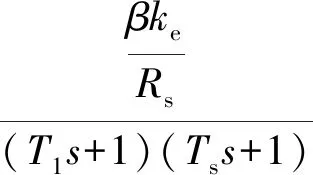
3 系统仿真与分析
3.1 仿真平台
3.2 仿真效果分析

4 结 语

