概念格的对象渐减更新算法
王静宇 郑雪岩
(内蒙古科技大学信息工程学院 内蒙古 包头 014010)
0 引 言
形式概念分析是Wille[1]于1982年提出的,它的核心数据结构是概念格,是根据描述现实世界的形式背景建立起来的,描述了对象和属性之间的关系。在现实生活中,对象和属性不断发生变化,概念格也随之改变,因此研究概念格的维护是十分必要的。Godin等[2]提出了一种渐进式的概念格构造算法;概念格的应用涉及到了多个领域,例如信息检索、知识管理、软件工程[3-4]等;吴刚等[5]提出了扩展概念格的维护;谢霖铨等[6]提出了粗糙概念格构造的算法;智慧来等[7]提出了概念格的第一类维护和第二类维护;刘保相等[8]提出了一种区间概念格结构;智慧来等[9]研究了以关系为更新粒度的概念格增量维护;张春英等[10]提出了基于属性幂集的渐进式生成算法;文献[11-12]提出了增加一个对象或属性时的概念格维护;崔芳婷等[13]提出了基于约束的模糊概念格构造算法;王春月等[14]提出了基于二元关系消减的概念格维护算法。
删除对象后概念格会发生改变,为了防止重新构造概念格耗费大量时间,本文借鉴了张磊[15]的构造概念格的方法,对删除对象后概念格的结构变化以及概念之间的联系进行改进,提出一种概念格的对象渐减更新算法。
1 相关概念
形式背景是一个矩阵图,表示对象和属性之间的二元关系,矩阵的行表示属性m、列表示对象g,形式背景记为O=(G,M,R),其中:G是对象的集合;M是属性的集合;R表示G和M之间的关系。若g行与m列的交叉处为1,即gRm=1,则表示对象g具有属性m,相应地,gRm=0表示对象g不具有属性m。形式背景如表1所示。
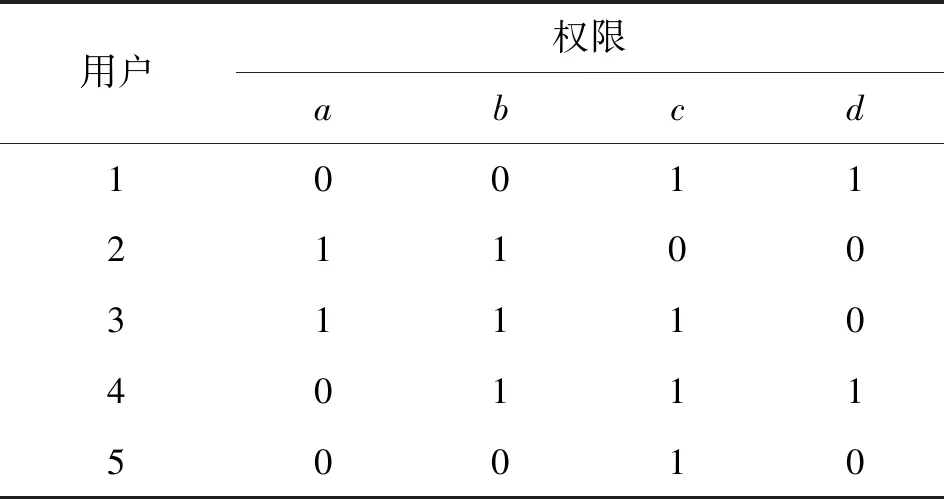
表1 形式背景示例
定义1若X是G的子集,Y是M的子集,令:
(1)h(X)={m∈M|g∈X,gRm}。
(2)h(Y)={g∈G|m∈Y,gRm}。
如果X、Y满足h(X)=Y、h(Y)=X,则称(X,Y)是形式背景的概念Node,简称N,X(x1,x2,…,xn)是概念(X,Y)的外延,记为Extension(N),简称E(N),Y(y1,y2,…,yn)是概念(X,Y)的内涵,记为Intension(N),简称I(N),概念的集合记为NS(O)。
定义2设(X1,Y1)和(X2,Y2)是形式背景的两个概念,如果X1⊆X2,且不存在X3,使得X1⊆X3⊆X2,则称(X1,Y1)是(X2,Y2)的子概念,(X2,Y2)是(X1,Y1)的父概念,记为(X1,Y1)≤(X2,Y2)。(X1,Y1)和(X2,Y2)是一对父子概念对,所有父子概念对连在一起构成了概念格的Hasse图,在Hasse图中,把连接两概念之间的线称为边。表1的形式背景所对应的概念格的Hasse图如图1所示。
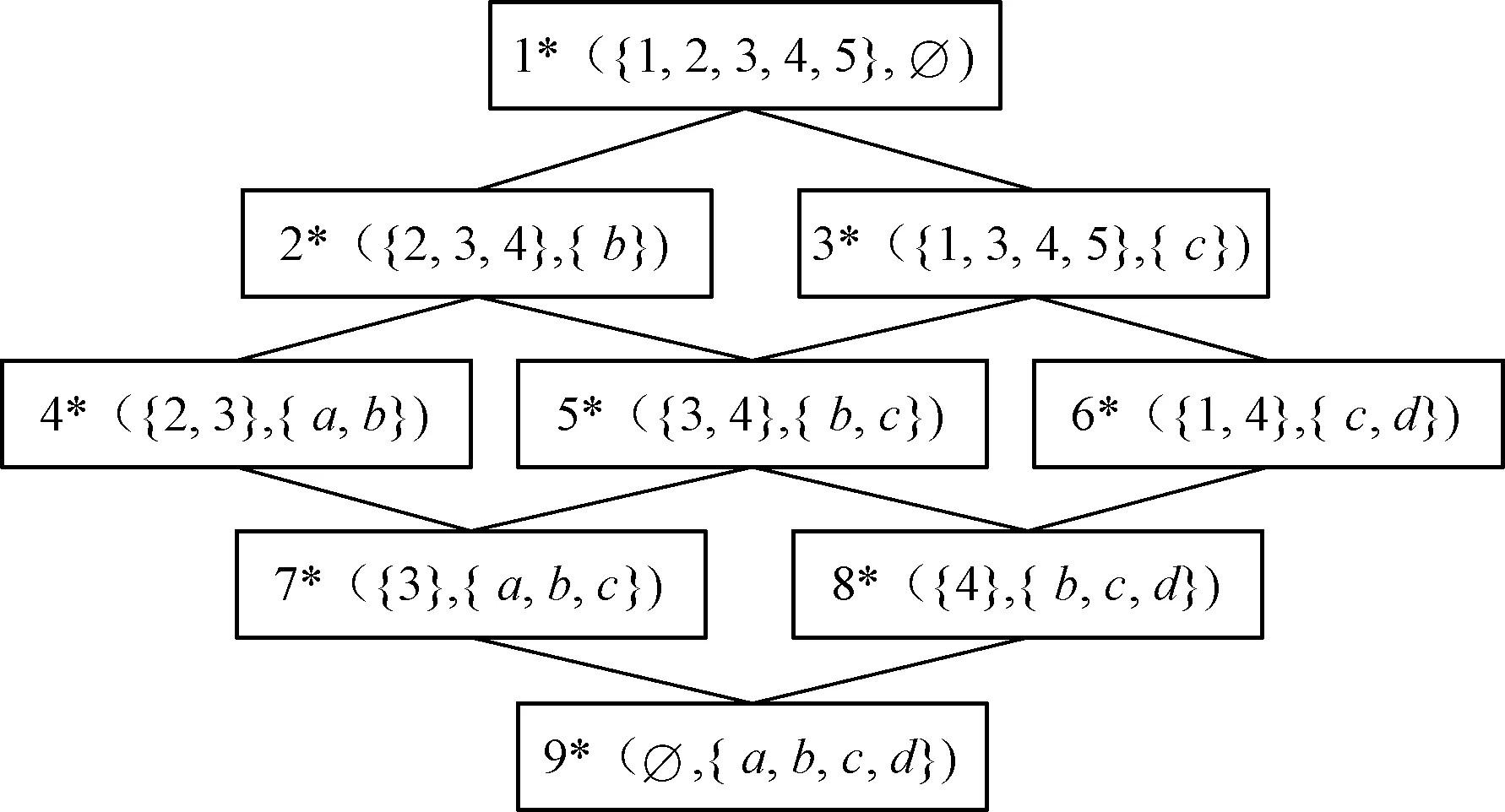
图1 表1的形式背景对应的概念格的Hasse图
定义3对于概念(X1,Y1)和概念(X2,Y2),X1⊆X2,如果(Xx,Yx)是(X1,Y1)到(X2,Y2)之间的路径上唯一的一个概念,则称(Xx,Yx)是(X1,Y1)和(X2,Y2)的枢纽概念。
2 概念格
2.1 概念的分类
记删除对象x后的概念格为L(O|-{x}),原概念格为L(O),L(O)中的概念由如下三种类型组成:
(1) 不变概念:指外延中不含删除对象x的概念,即x∉Extension(N)的概念。这一类概念的集合用FS-{x}(O)来表示。

(3) 删除概念:指外延包含x,∃Extension(N1)=E(N)-{x}的概念。这一类概念的集合用DS-{x}(O)来表示。
2.2 概念的分析
定理1删除对象x后,原概念格中的不变概念不发生任何变化,直接保留到新的概念格中,即FS-{x}(O)⊆NS(O|-{x})。
定理2删除对象x后,更新概念的外延减去x即可成为新概念格中的概念,即VS-{x}(O)⊆NS(O|-{x})。
定理3删除对象x后,新概念格中的概念是由FS-{x}(O)和VS-{x}(O)组成的。
由上文可知,新概念格由不变概念和更新概念组成,删除对象后,不变概念不发生任何变化,直接保留到L(O|-{x})中,更新概念的外延减去x,即可成为L(O|-{x})中的概念,删除概念需删掉。
定理4包含所有对象的概念是头概念,头概念必定是更新概念,因此构造L(O|-{x})时不需要判断它的类型,直接更新外延即可。
定理5包含所有属性的概念是末概念。末概念的外延不包含任何对象,所以末概念必定是不变概念,构造L(O|-{x})时不需要判断它的类型。
2.3 边的分析
概念格是由概念和概念之间的边组成的,因此删除某一个对象后,不仅要考虑新概念格中概念的组成,还要考虑概念之间的边的变化。边都是存在于父概念和子概念之间的,所以我们来根据父概念和子概念之间的关系去判断边的变化。
定理6不变概念的子概念还是不变概念。
由定理6可知,以下两种情况不存在:
(1) 父概念为不变概念,子概念为删除概念。
(2) 父概念为不变概念,子概念为更新概念。
定理7如果父概念和子概念中没有一个是删除概念,则该父概念和子概念之间的边不需要改变,保留到新的概念格中。
由定理6和定理7可知,以下三种情况不需要调整边:
(1) 父概念是更新概念,子概念是不变概念。
(2) 父概念是更新概念,子概念是更新概念。
(3) 父概念是不变概念,子概念是不变概念。
定理8删除对象x后,若Extension(N)-{x}=∅,则在删除概念的父概念与其子概念之间增加一条边;若Extension(N)-{x}!=∅,且概念是其父概念与子概念之间的枢纽概念,则在删除概念的父概念与其子概念之间增加一条边。
定理9一个删除概念的子概念中只有一个不变概念,其他都是删除概念。
由定理9可知,父子概念分别为删除概念和更新概念的情况不存在。
综上所述,删除对象后边的关系如表2所示。
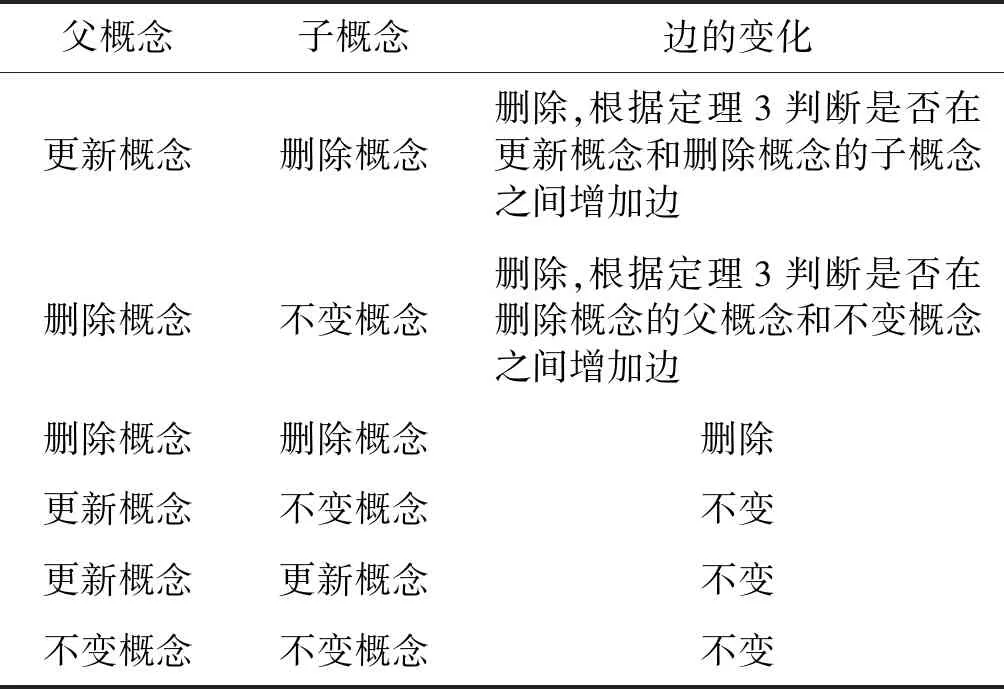
表2 删除对象后各父概念与子概念之间边的变化
根据前文中对删除对象后概念和边的分析可知:删除对象后,父概念与子概念的类型有一定的联系,父概念与子概念之间的边也存在一定的变化规则。据此提出一种渐进式的概念格构造算法,即对象渐减更新算法。
3 算法描述
3.1 算法思想
根据前文所述可知,不变概念的子概念依然是不变概念,删除概念的非不变子概念是更新概念,不需要判断这两种概念的类型。算法主要解决的是删除一个对象后,如何得到一个新的概念格,该算法采用广度优先遍历的顺序,以头概念为顶点,依次对概念进行处理,因此访问某个概念的时候,它的父概念已经被访问过,进而该算法可根据父概念的类型来判断子概念的类型。
该算法不需要判断不变概念的子概念,所以只需要判断更新概念和删除概念的子概念即可。在该算法中设未被访问过的概念的visited的值为0,被访问过的概念的visited的值为1。概念的visited的值为0时算法向下执行,所有概念的visited的值为1时算法结束。
3.2 对象渐减更新算法
算法1的相关术语:Child(FS)用来表示不变概念的子概念;Child(VS)用来表示更新概念的子概念;Child(DS)用来表示删除概念的子概念。
在算法1中,直接对头概念进行更新,然后算法向下执行。如果是更新概念的子概念,则判断其类型并进行相应的处理(4-17行);如果是删除概念的非不变子概念,则该概念必然是删除概念,此时调用算法2对概念进行删除操作并修改相关的边的关系(18-22行),直到所有概念的visited的值为1。
算法1对象渐减更新算法
输入:原始概念格L(O),删除对象x。
输出:删除对象x后的格L(O|-{x})。
1.Extension(N):=Extension(N)-{x};
//更新头概念
2.WhileN.visited:=0
///当概念未被访问过的时候
3.For (N∉Child(FS))
4.For (N∈Child(VS))
5.If (x∉Extension(N))
6.doNotChange;
//不做改变
7.N.visited:=1;
8.Else If (∃Extension(N):=Extension(N)-{x})
9.Delete(L(O),N);
//调用算法2,删除概念并调整相应的边
10.N.visited:=1;
11.Else If
12.Extension(N):=Extension(N)-{x};
//更新概念的外延
13.N.visited:=1;
14.End If;
15.End If;
16.End If;
17.End For;
18.For (N∈Child(DS))
19.If(N∈Child(DS) and 非FN)
20.Delete(L(O),N);
21.N.visited:=1;
22.End For;
23.End For;
24.End While;
25.ReturnL(O|-{x});
算法2的相关术语:NChild用来表示概念的子概念;NParent用来表示概念的父概念。
该算法用于将概念删除并调整其相关边的关系,在该算法中,符合下面两种情况的需要添加边:
(1) 对于外延不只由x组成的概念,如果它是任意两个概念之间的枢纽概念,则在这两个概念之间添加边。
(2) 对于外延只由x组成的概念,直接在其父概念与子概念之间添加边。
算法2删除算法
输入:概念格L(O),删除概念N。
输出:删除概念N后的格L(O|-{x})。
1.If (Extension(N)-{x} !=∅ andN是NParent→NChild的枢纽概念)
2.Then 删除与N相关的边,添加边NParent→NChild,删除N;
3.Else删除与N相关的边,删除N;
4.If (Extension(N)-{x}=∅)
5.Then 删除与N相关的边,添加边NParent→NChild,删除N;
6.Else 删除与N相关的边,删除N;
7.End
4 算法示例及实验验证
4.1 算法示例
以图1为例,删除对象4,算法的维护过程如下:
(1) 头概念是更新概念,直接更新。
(2) 概念2*的外延去除对象4后与概念4*的外延相同,因此2*是删除概念,删除2*,删除边(1*,2*),删除边(2*,4*),删除边(2*,5*),且2*是1*与4*之间的枢纽概念,故添加边(1*,4*)。
(3) 3*的外延减去4后与其任何一个子概念延都不相等,故3*为更新概念,更新3*的外延。
(4) 因为4*和5*都是2*的子概念,且4*是不变概念,故5*为删除概念,删除5*,删除边(3*,5*),删除边(5*,7*),删除边(5*,8*),因为5*是3*和7*之间的枢纽概念,故增加边(3*,7*)。
(5) 6*的外延减去x后与其任何一个子概念延都不相等,故6*为更新概念,更新6*的外延。
(6) 7*的外延不包含对象4,故7*为不变概念,不作任何改变。
(7) 8*的外延只包含对象4,符合E(N)-{x}=∅,故删除概念8*,添加边(6*,9*),删除边(6*,8*),删除边(8*,9*)。
删除对象4后的概念格对应的Hasse图如图2所示。
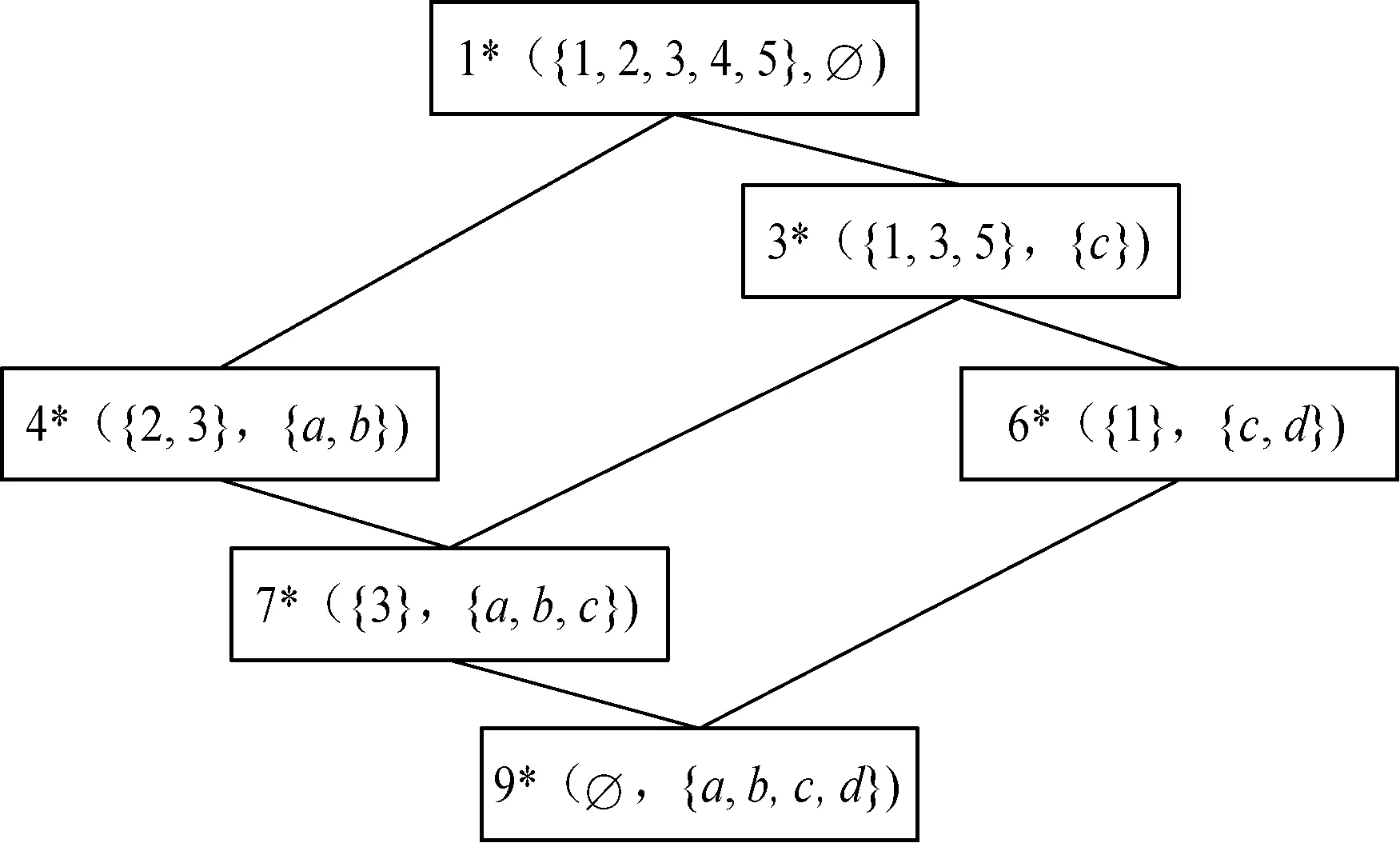
图2 删除对象4后的概念格
4.2 实验验证
删除某一对象后,该渐进式维护算法不需要重新构造概念格,只需对更新概念、删除概念及其相关的边进行处理,因此在很大程度上减少了概念格的维护时间。该算法还包含以下几个优点:
(1) 不需要判断头概念的类型,可直接更新头概念。
(2) 该算法可根据父概念的类型来判断子概念的类型,所以可以减少概念类型的判断次数。
(3) 若概念的外延中只包含删除对象x,则不必判断概念是否是两个概念之间的枢纽概念,可直接在概念的父概念和其子概念之间添加边。
实验一验证需调整的概念占总概念的比例。
随机生成形式背景,属性个数固定为20,对象数目从10到100,每次增加10个对象来进行实验。实验结果如图3所示,纵轴表示需要调整的概念占全体概念的比例;横轴表示对象的数量;两条折线的对象属性间存在关系的概率分别为0.20和0.25。当删除一个对象时,需要调整的概念所占比例较小,而且随着对象数的增加,这个比例会更小,所以相对于重新构造概念格,本文这种渐进式的方式的效率会比较高。
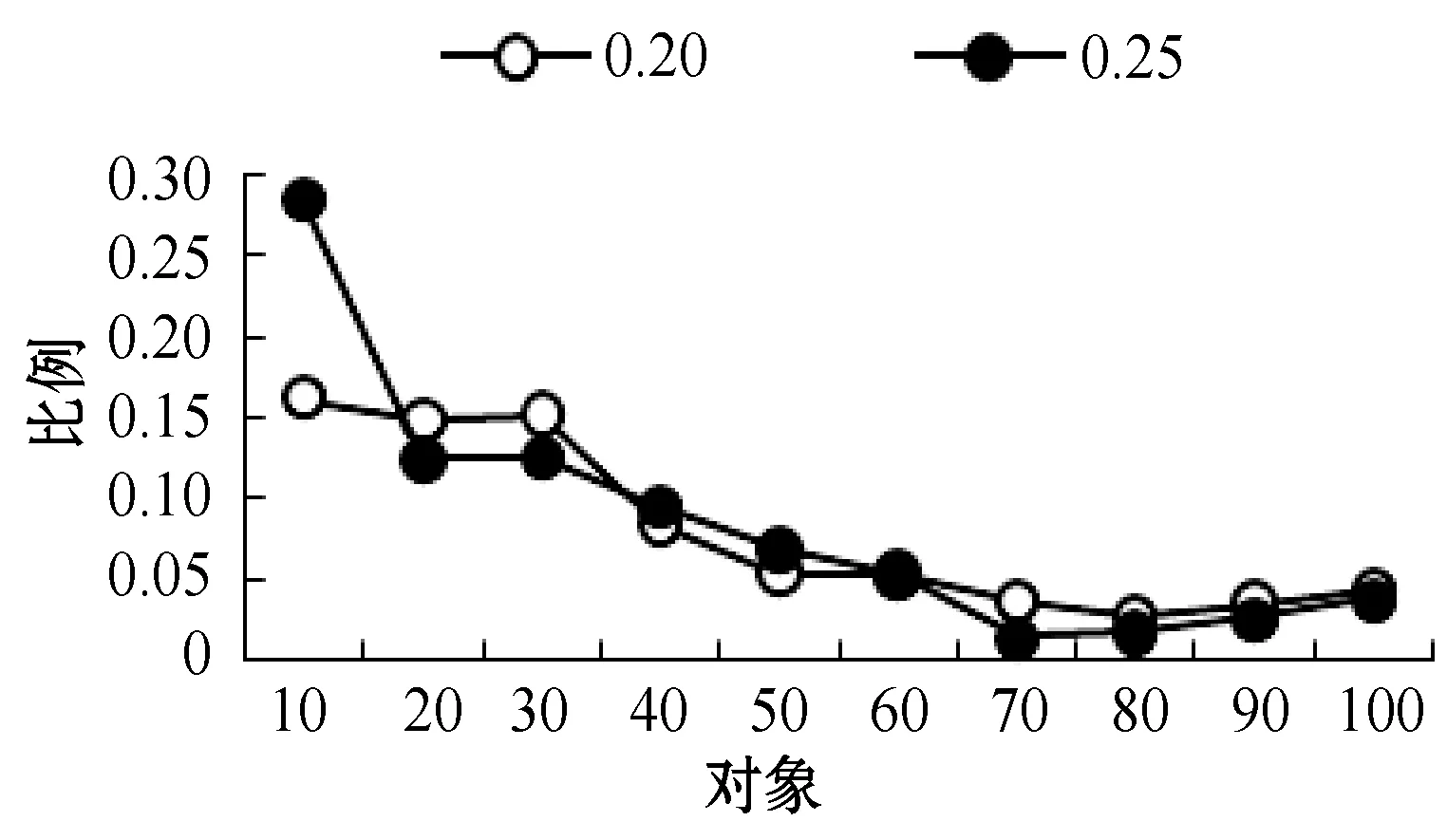
图3 需要调整的概念占总概念的比例
实验二主要从时间方面验证算法的有效性。
为了验证本文优化算法的结果,与AddIntent[16]算法和In-Close[17]算法进行对比。AddIntent算法是最快的基于对象的概念格构造算法之一,In-Close算法是近年出现的最快的概念格构造算法之一。我们随机产生了三组数据,三个算法的性能都是这三组数据的平均值,属性的数目都为20,对象数目从100到900,每次增加50个对象来测试算法的执行时间。相对于In-Close算法和本文算法,AddIntent算法消耗的时间比较多,放在同一个图中对比不明显,因此分开来对比。图4是本文算法与AddIntent算法的对比,图5是本文算法与In-Close算法的对比,两个图的横轴都表示对象,纵轴都表示算法执行所用的时间。实验结果表明,随着对象数目的增加,三个算法所花费的时间都在增长,但本文算法所用时间明显低于AddIntent算法和In-Close算法。因此本文的算法明显减少了构造概念格所花费的时间。
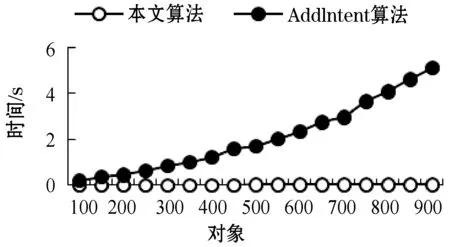
图4 对象数目增大时本文算法与AddIntent算法的时间性能
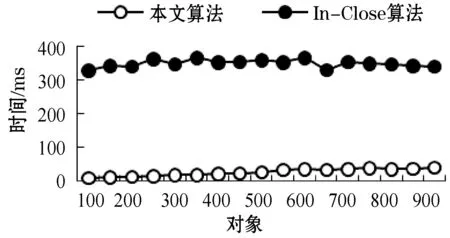
图5 对象数目增大时本文算法与In-Close算法的时间性能
5 结 语
本文根据删除对象后,概念格中父子之间的边以及概念的变化,提出一种概念格渐进式更新算法,该算法减少了概念格构造的时间。
该算法对删除概念的子概念的访问是有序的,而删除概念的非不变子概念肯定是删除概念,如果先找出不变子概念,就不需要判断其余子概念的类型。对于同一个概念的子概念,如果删除概念在不变概念前的情况较多,则算法的执行速度可能会更快,下一步将研究这一方面的内容。

