一种改进的网格多边形online探索算法

谢玉莹 包敏泽 胡秀婷 蒋 波

(大连海事大学信息科学技术学院 辽宁 大连 116026)

0 引 言

利用移动机器人探测未知环境的路径规划问题可描述为：在一个边界信息未知的网格区域P中，机器人从初始位置出发，在区域P内做上、下、左、右四个方向上的移动，但每次仅限移动一个单元格，要求机器人能完全遍历给定的网格区域，最终返回到出发点，并使得其移动路线的长度达到最短。该问题一直受到计算几何学[1-4]、机器人学[5]领域学者的广为关注，并取得了较好的研究成果[6-11]。该问题的研究成果可在自动割草机、自动浇水机、扫地机器人等智能设备的开发中得到广泛应用，因此值得进一步展开研究。

在online探索问题研究中，要探索的区域往往是边界信息未知的，因此一般难以设计出最优的探索策略[12-15]。为了对比分析online探索问题的求解策略，通常引入“竞争比”的概念。所谓竞争比，它可定义为探索策略的代价(可以是探索路径的长度或探索所需要的时间)与边界信息已知情形下的最优搜索策略所需代价的比。由于边界信息已知，所以往往能够设计出好的搜索策略，甚至是最优搜索策略。但是，当边界信息未知时，机器人往往需要反复探索，所以竞争比通常大于1。显然，online探索问题的改进方向就在于设法降低算法的竞争比。

针对网格区域的online探索问题，可通过对网格做深度优先(DFS)来实现竞争比为2的简单探索。对于正方形单元格，文献[6]提出了SmartDFS算法，将竞争比优化为4/3。文献[8]将该问题的竞争比的上界更新为5/4；文献[15]证明了三角形单元格不存在竞争比优于7/6的算法；六边形单元格不存在竞争比优于13/11的算法[15]。

online探索算法可用于解决一些实际应用问题。文献[9]提出了一个带洞网格多边形中哈密尔顿路径存在的必要条件，并证明了网格图中哈密顿路径可在线性时间内算出；文献[7]进一步研究了基于online探索的疏散问题，将竞争比从19.5降低为不超过17.5，使受灾人员能更加快地速撤离出网格类型的受灾区域。

为方便研究，假设机器人要探索的网格区域为P，P中每个网格的边缘是垂直或水平的，且每个网格为单位长度的正方形。P的边界是一个简单多边形，并以网格的边作为边界。除了边界外，P的内部不存在阻碍机器人移动的任何障碍物。

在这类问题研究中，通常对机器人的能力做不同约束：除了机器人的视距范围外，还有机器人的感知范围、移动限制、记忆能力、标记能力等。本文对机器人的能力定义如下：机器人每次移动距离为一个单位长度，移动方向为基于前进方向的上、下、左、右；机器人具有足够的记忆能力，但却没有先验能力；机器人在当前位置能且仅能感知到3/2个单位长度范围内的网格状态(在P的内部或者在P的边界)。

在本文研究中，约定机器人具有视觉范围，但范围是受限的。文献[6]约定机器人的视觉范围为一个正方形单元格，本文对之做了改进，让机器人的可视范围最大化，并将机器人的视觉范围定义为相应单元格的外接圆，在理论上尽可能充分利用机器人的可视范围，设计出性能更优的探索策略。从实际应用的角度看，机器人的视距范围是圆形更切合生活实际。例如，在考古或救灾等场合需要探索一些恶劣环境时，使用机器人探索是最安全、适宜的，而这时的机器人视觉范围通常是受限的，因此为机器人附加一些约束条件是具有可操作性与实际意义的。

1 online探索策略

由于P为由整数个网格单元组成的简单多边形，P的内部无阻塞(如图1所示)，所以遍历多边形P的机器人路径应包括在P中。文献[6，8]中的机器人在遍历多边形P时，其位置处于单元格中心，有效遍历区域仅为机器人视觉范围的内接正方形，本文扩大了机器人的可视范围，即遍历范围大于文献[6，8]所定义的范围如图2所示。其中，阴影正方形是改进之前的机器人视觉范围，而整个圆圈则是改进后的机器人视觉范围。利用扩大的视觉范围，让机器人从P的某单元格边界出发，逐个遍历P中的单元格，最终返回出发点。

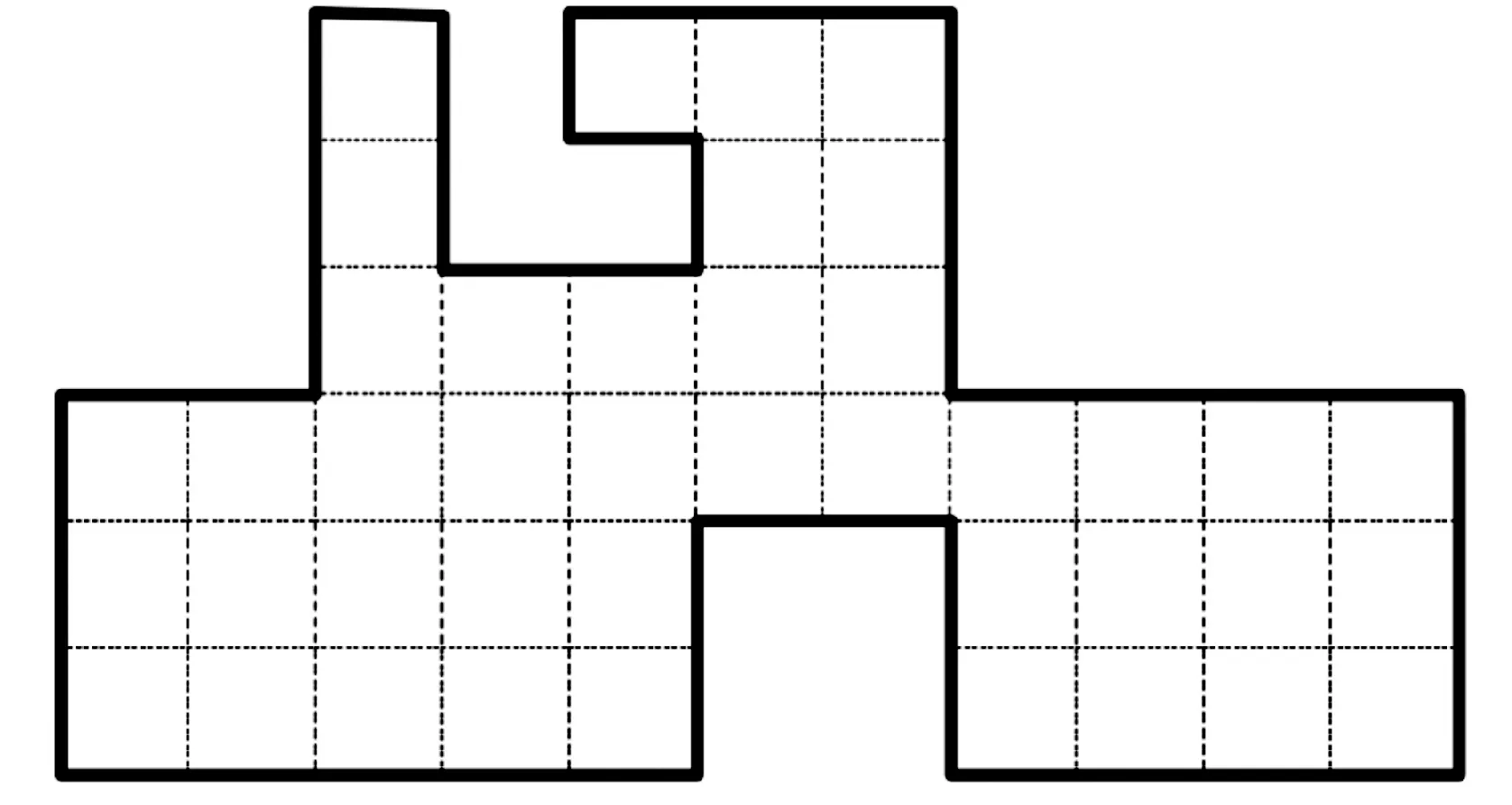
图1 内部无阻塞的简单网格多边形

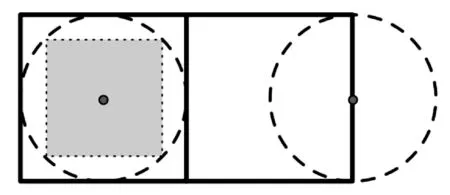
图2 机器人不同的可视范围

不失一般性，假设机器人的初始位置在网格多边形的右上角，即机器人的右边是多边形的边界，左边或下边是可访问的单元格，如图3所示。若机器人的初始位置不满足该约定，则可预先将它移动到相应的位置，且初始所做的移动操作不会影响本文的结果。

图3 可视范围最大情形下机器人遍历网格多边形的示例

机器人在单元格边缘上移动时，往往难以发现机器人行走路径与网格单元间的关系，为此，本文将P整体向右平移1/2个单元格，并在P的最左边增加一列单元格，称该操作为P+处理，经过P+处理得到的多边形为P+多边形。如图4所示，其中阴影部分为添加的单元格。

图4 多边形P+

P+处理有利于竞争比分析，且并不改变机器人对P的遍历路径。由于P+处理后机器人的初始位置约定为多边形P+右上角的单元格，所以机器人初始方向右边的位置可标记为返回单元格(如图4中的斜线阴影单元格所示)。在探索过程中，返回单元格可作为一般单元格在最后被访问。

2 算法设计

在SmartDFS算法[6]和算法A[8]的基础上，本文提出了SmartDFS-OPT算法。将机器人遍历过的单元格(包括机器人当前所在的单元格)记为已访问单元格，未遍历的单元格记为未访问单元格，并对未访问单元格做进一步细分。

定义1若未访问单元格满足下列条件，则称之为A类单元格。

(1) 机器人当前位置与该单元格相邻。

(2) 该单元格周围的四个位置中有3个或4个位置，要么是已经访问过的单元格，要么是多边形边界及其外部。

显然，A类单元格可分为包含边界边的边界A类单元格和不包含边界边的内部A类单元格。

定义2若未访问单元格满足下列所有条件，则称之为B类单元格。

(1) 该单元格位于机器人当前位置的前方(机器人前进方向上的下一个单元格)。

(2) 已访问单元格与该单元格的集合恰好包围了一块未访问单元格区域P′。

图5给出了上述定义的几个示例，其中，图5(a)中阴影部分的单元格为边界A类单元格；图5(b)中阴影部分的单元格为B类单元格，斜线阴影单元格为内部A类单元格。

图5 A类单元格和B类单元格示例

算法SmartDFS-OPT描述如下：

1)设置未访问单元格堆栈N和存储A、B类单元格的未访问单元格堆栈V，并设置堆栈N和V的初值为空。

2)机器人每移动一步，均做以下更新：

(1) 将机器人周围的未访问单元格按如下规则分别加入N或V中。

① 若为内部A类单元格或B类单元格，机器人将按照右、上、左的顺序访问它们，将未访问单元格按优先级顺序加入栈N；

② 若为边界A类单元格，机器人将按照左、上、右的顺序访问它们，将未访问单元格按优先级顺序加入栈N；

③ 若为非A或B类单元格，机器人将按照左、上、右的顺序访问它们，将未访问单元格按优先级顺序加入栈V。

(2)确定机器人的目的地。

① 若堆栈V非空，则目的地=堆栈V顶部；

② 若堆栈V空，堆栈N非空，则目的地=堆栈N顶部；

③ 若堆栈V和堆栈N皆空，则目的地=机器人初始位置。

3) 若机器人回到初始位置，则N和V为空，算法结束。

4) 否则，重复执行步骤2)。

由于本文将文献[8]提出的死端概念进一步划分为A类单元格，因而很好地避免了算法A[8]因局部遍历而得到的最坏情形，如图6和图7所示。

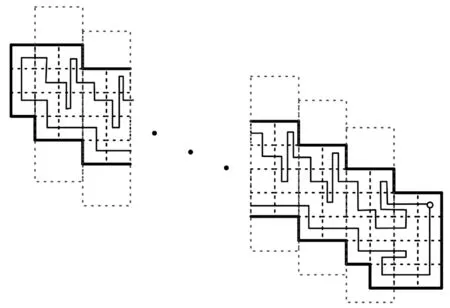
图6 算法A的最坏情形

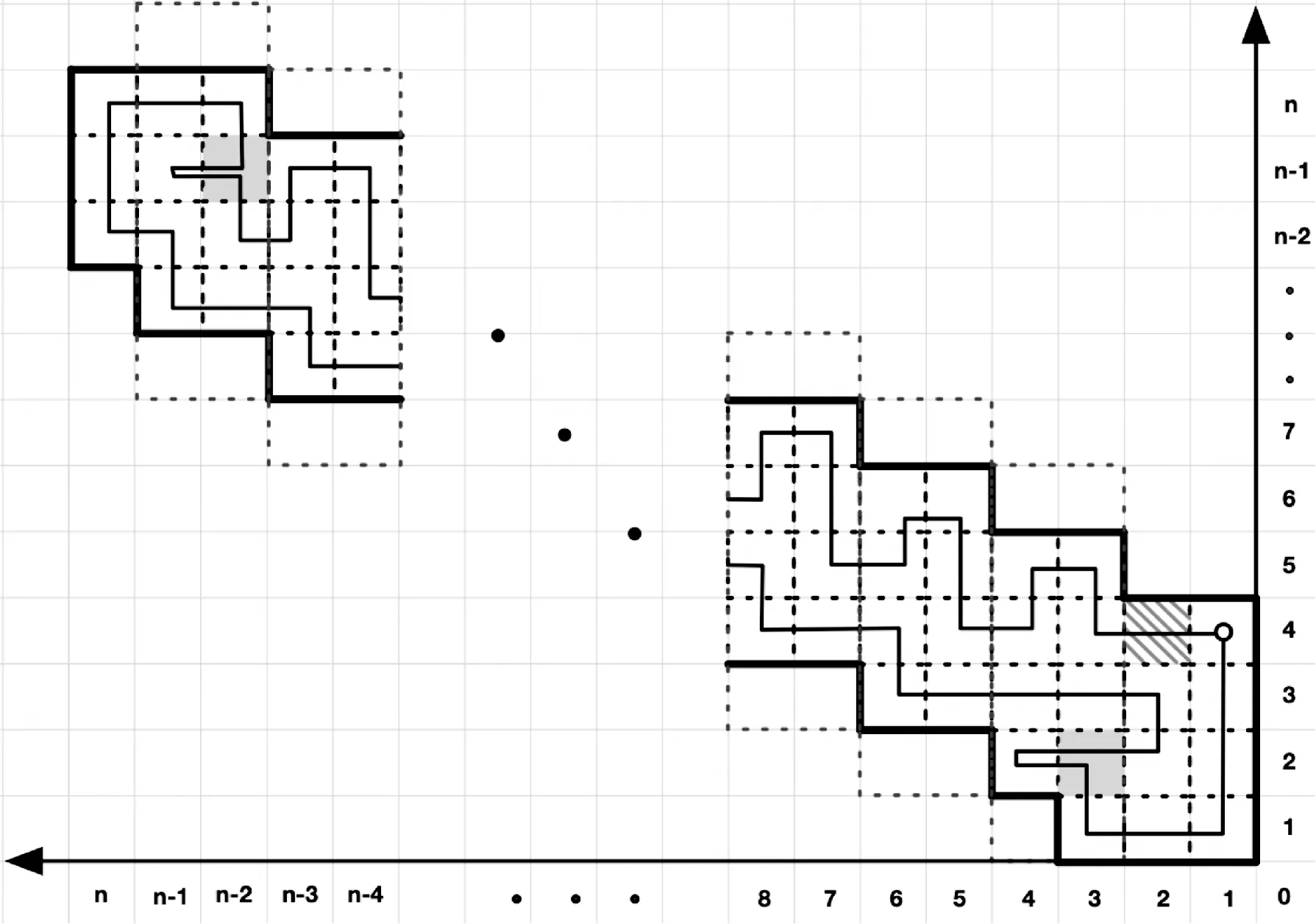
图7 用SmartDFS-OPT算法解决图6所示的最坏情形

图7所示的解决方法为SmartDFS-OPT算法的执行结果，其具体描述如下：

用平面坐标标记每个单元格，并假定机器人的初始位置为(1, 4)，并标记(2, 4)为返回单元格。机器人沿多边形边缘移动至(3, 2)，此时它识别到(4, 2)、(3, 3)和(2, 2)为未访问单元格，其中(4, 2)和(2, 2)为A类单元格。机器人优先访问边界A类单元格(4, 2)，再通过最短路径访问内部A类单元格(2, 2)，然后根据最短的未访问路径回到多边形边界单元格(6, 3)，…。当机器人遍历到(n-2,n-1)时，发现(n-1,n-1)和(n-2,n-2)都是内部A类单元格，故优先访问右侧单元格(n-1,n-1)，直至从预留的返回单元格返回初始位置。

3 算法性能分析

3.1 竞争比分析

由于机器人具有记忆功能，所以能够根据局部视图和遍历记录来区分单元格的类型。假设用Ti来表示重复访问单元格i的次数，则有：

T=T2+2T3+…+(i-1)Ti

i=2,3,…

(1)

若多边形P+中有X个单元格，则探索P+需要遍历的单元格数量为：

S=X+T

(2)

引理1对于任意X>2的网格多边形P+，机器人通过SmartDFS-OPT算法探索网格多边形所走的路径有：

(3)

式中：c为常数。

证明：

1) 若机器人在对多边形探索过程中没有遇到内部A类单元格和B类单元格，则S不仅恰好符合式(2)且满足式(3)关系。

2) 若机器人在对多边形探索过程中遇到了B类单元格，则可把多边形分成多个子多边形分别处理，且综合结果也满足上述关系。

3) 若机器人在对多边形探索过程中遇到了内部A类单元格，则该多边形存在骨架[8]，可对基本骨架做局部遍历分析。假设一个存在基本骨架的最小反例多边形P，满足式(3)，那么P的基本骨架一定包括图8所示的几种情形，或断开连接。

图8 基本骨架的最小反例

断开连接的情形可分别处理，容易得到证明。对于以图8所示的6种骨架结尾的情形，可组合得到20种局部修改类型，通过这些局部修改，可在不改变遍历方式的前提下，分析所有可能情形，求得Δ的值：

(4)

其中，

S′=S(P)-S(P′)

(5)

C′=C(P)-C(P′)

(6)

T′=T(P)-T(P′)

(7)

图9给出了一个局部修改的示例，其中S′=4，X′=4，T′=0，则Δ=-2/3<0。

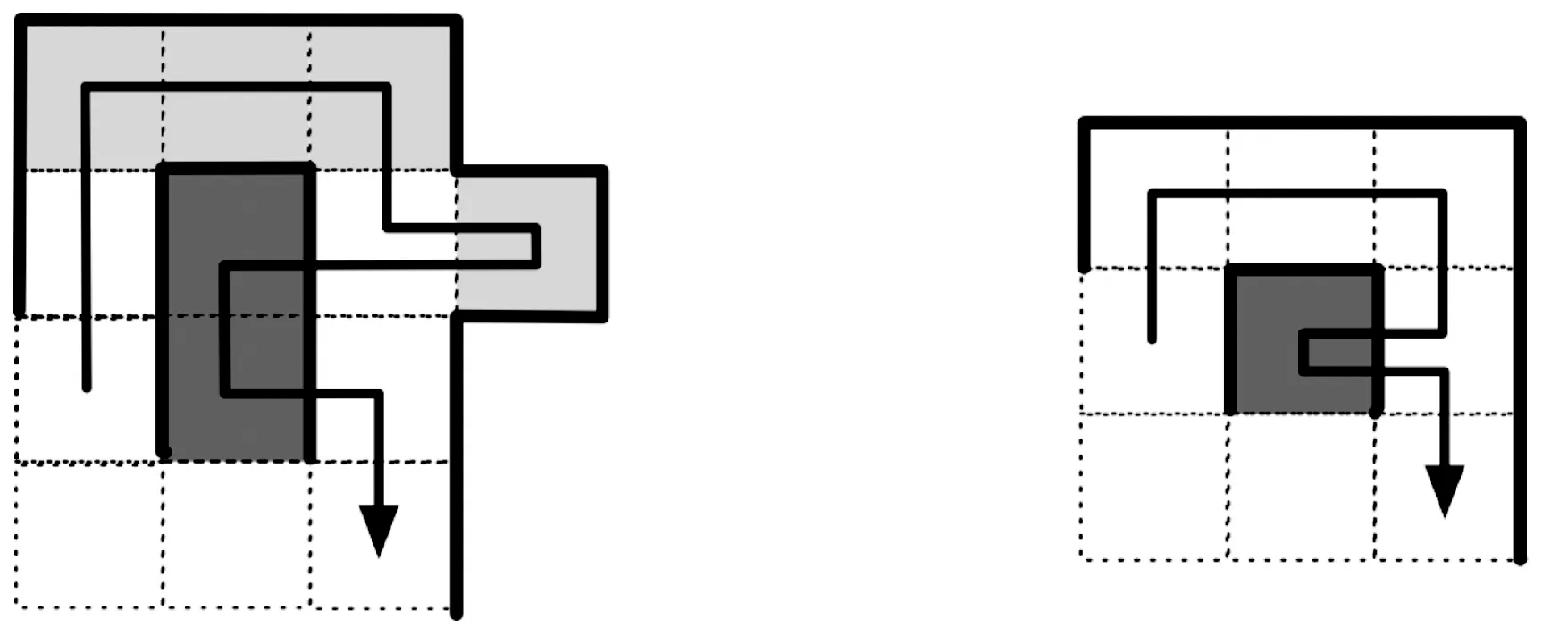
图9 局部修改实例

其余19种情形可做类似的处理，均能得到Δ≤0的分析结果。限于篇幅，不一一列举。

以上情形包括所有可能的例外情形，由于均有Δ≤0，所以引理1得证。

定理1可视范围最大化情形下机器人对未知网格区域做online探索的竞争比不大于7/6。

证明：

由于本文引入了边界A类单元格，且边界A类单元格位于P+的最外层，所以确定为优先访问对象，且内部A类单元格也是优先访问对象，这样就缩短了返回路径的长度。当边界A类单元格和内部A类单元格位于机器人当前位置的左右两侧时，可找到局部遍历分析时的最坏情形，如图10所示。

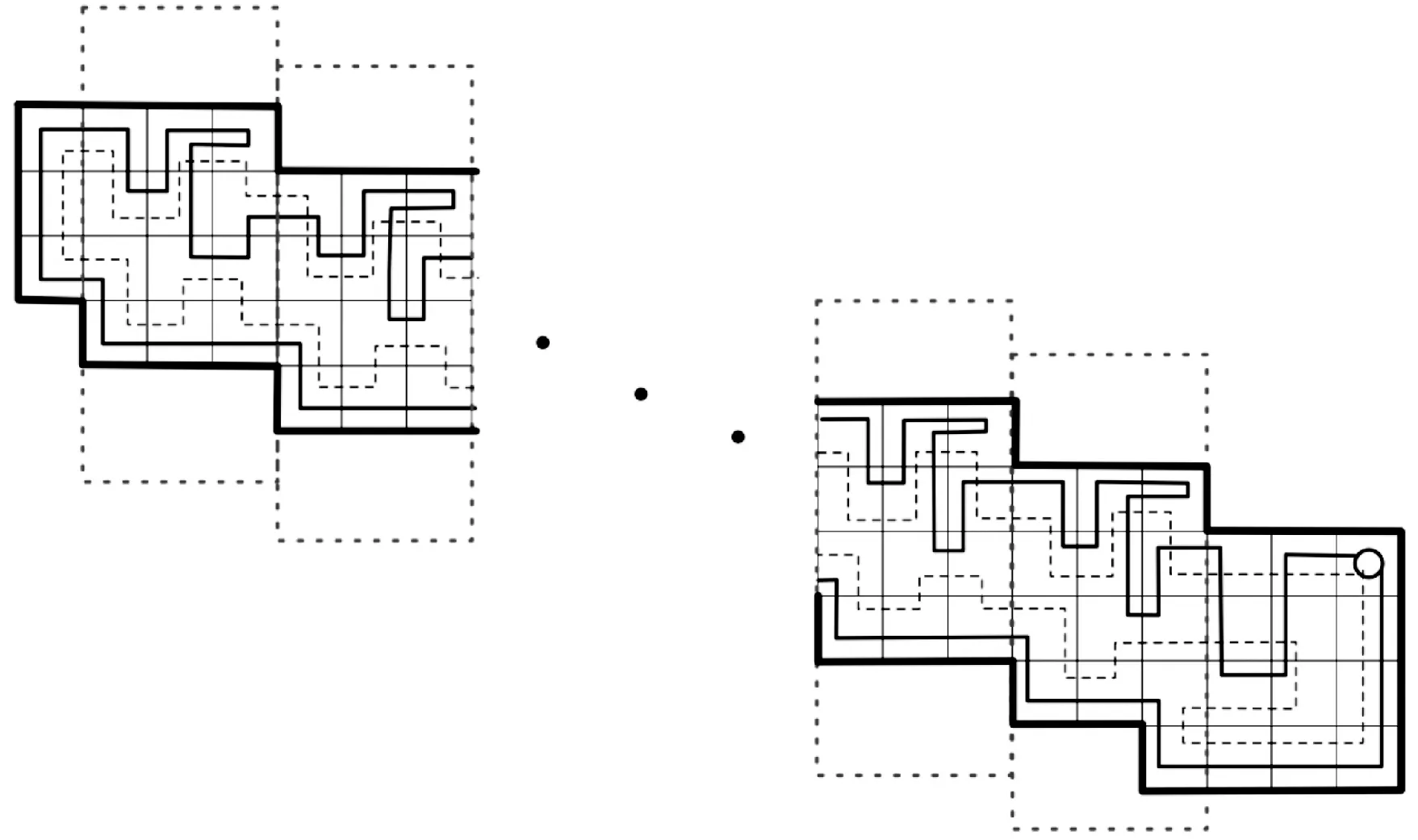
图10 算法SmartDFS-OPT的最坏情形

因此，对于一般情形，有：

(8)

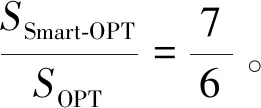
证毕。

综上，SmartDFS-OPT算法的竞争比不超过7/6，即可视范围最大化情形下机器人对未知网格区域的online探索的竞争比上界为7/6。因为SmartDFS算法[6]的竞争比下界为7/6，SmartDFS-OPT算法是通过扩大视觉范围而对其做的改进，所以SmartDFS-OPT算法的竞争比下界也为7/6，也就是说，SmartDFS-OPT算法竞争比的上界和下界均为7/6，即SmartDFS-OPT算法为求解网格多边形online探索问题的最优算法。

3.2 算法实现

为验证SmartDFS-OPT算法的可靠性，本文通过编程对其进行了仿真和对比试验，实验截图如图11所示，对于输入数据182，系统随机生成了一个有182个单元格的网格多边形，并分别给出了算法A[8]、offline算法、SmartDFS-OPT算法执行过程中机器人的遍历路径、遍历路径长度以及竞争比。

图11 实验截图

表1给出了20组随机实验的实验结果。

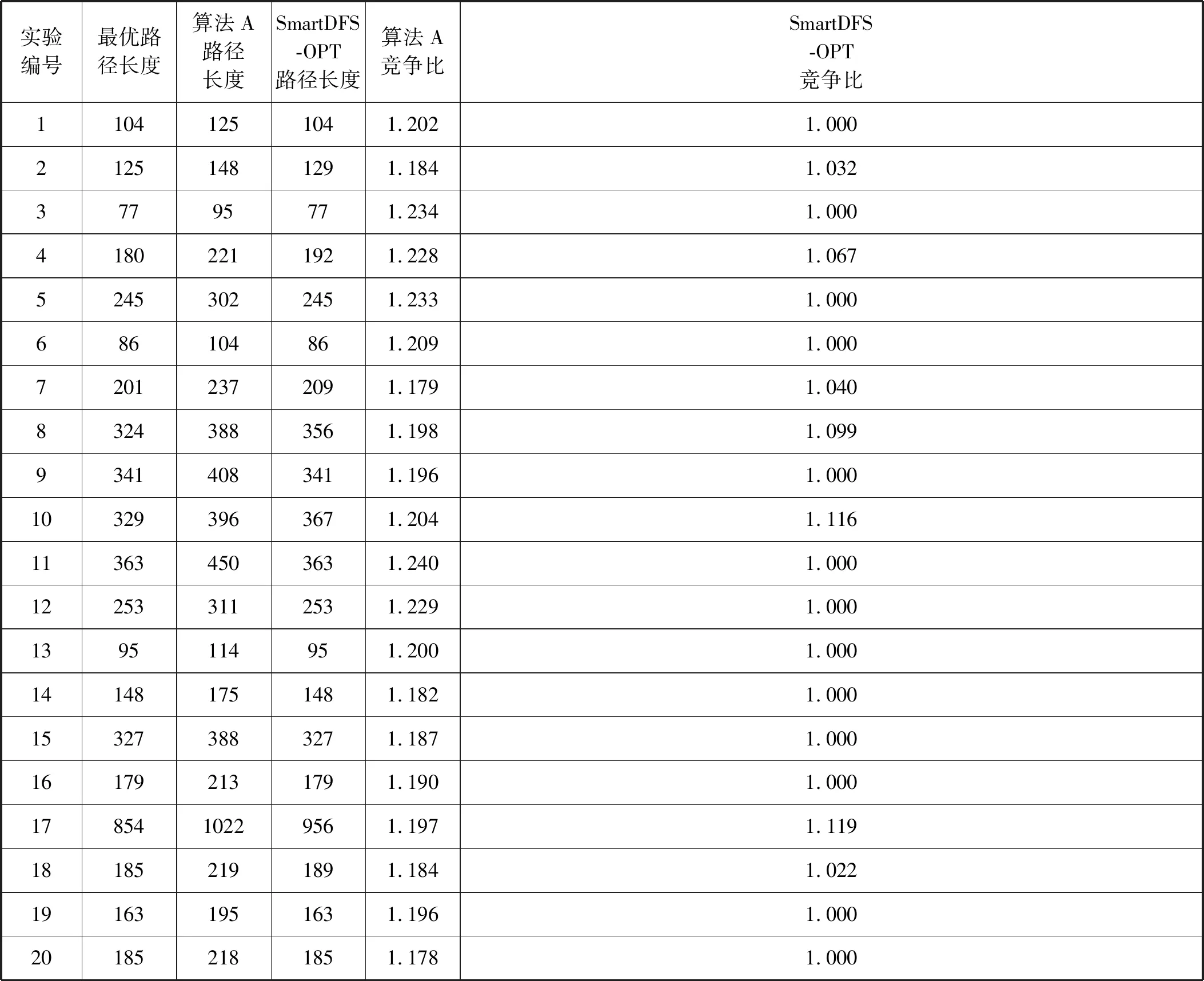
表1 SmartDFS-OPT算法和算法A的对比试验

实验数据显示，SmartDFS-OPT算法的竞争比明显小于算法A[8]的竞争比且小于7/6，因此SmartDFS-OPT算法优于算法A。

4 结 语

本文提出了机器人视距最大化情形下网格多边形的online探索算法，使求解算法的竞争比从5/4降低为7/6，达到了理论分析结果的下界，即为性能最优的网格多边形online探索算法。同时，通过随机生成网格多边形作为测试数据，对比分析了理论分析结果与实验结果，验证了本文提出的算法SmartDFS-OPT的有效性。针对带洞的网格区域online探索问题，视距最大化方法能否适用等问题，有待于今后做进一步的研究。