基于有限时间扰动观测器的四旋翼编队控制

张 阅

(大连海事大学船舶电气工程学院 辽宁 大连 116026)

0 引 言

近年来四旋翼飞行器(以下简称四旋翼)因其结构简单、可操作性强且具有垂直起降与定点悬停等优点，在军事及民用领域得到了广泛的应用。比如，近海监察、区域搜索、灾害救援、农业植保、航拍和货物运输等[1-2]。然而在实际的应用过程中，四旋翼飞行时间短、载荷有限和覆盖区域小等局限性逐渐地显现出来。针对于上述问题，令多个四旋翼进行团队协作来共同完成任务是一种有效的解决办法，因此，对多四旋翼进行协同编队控制成为了目前的热点研究方向之一。

当前，四旋翼编队控制方法主要有leader-follower法[3]、基于行为法[4]、虚拟结构法[5]和图论法[6]等，但是对于在复杂飞行环境下所受的外界干扰，很少有文献能够说明以上控制方法可以对扰动进行有效的抑制。考虑到上述方法的不足，为进一步提高编队系统的控制性能，国内外的学者们提出了很多先进控制方法，比如反推控制[7]、模型预测控制[8]、自适应控制[9]和滑模控制[10]等。文献[7]应用反推控制策略解决了多个水下机器人的编队轨迹跟踪控制问题，但是该方法要求精确的系统模型，建模过程中产生的误差会影响系统的跟踪效果。考虑到编队系统的输入及状态约束问题，文献[8]采用了模型预测控制策略实现了多个移动卫星的编队跟踪问题。为解决四旋翼编队的一致性问题，文献[9]采用自适应控制策略实现了编队队形的形成与保持。在实际应用中，滑模控制策略作为一种鲁棒性较强的控制技术主要用于处理一类具有时变不确定性、易受外界扰动影响的非线性系统。文献[10]采用滑模控制策略使编队系统中每一个移动机器人的实际位置与期望位置误差能够渐进地稳定到零，进而使得编队中相邻个体之间保持恒定的距离。文献[11]将反推控制策略与滑模控制相结合，得到了较好的跟踪效果，但是采用两种时间尺度分离的方法需要更大的内环增益来保证闭环系统的稳定性，增加了控制器的设计难度。以上控制策略只有在时间趋于无穷大时误差变量才能收敛到原点附近的邻域中，无法在有限时间内收敛到零，因此以上具有渐进收敛特性的控制策略收敛速度慢、精度低。

为实现有限时间收敛性能，文献[12]提出了一种终端滑模控制策略，该方法响应速度快、控制精度高并具有强鲁棒性，同时具有的有限时间收敛特性是该方法的一大优势，被广泛地应用在机械臂控制及地面车辆、卫星等的编队控制中。然而在传统终端滑模控制中，由于存在负的分数次幂，奇异性的问题不可避免。为了解决该问题，文献[13]提出了一种非奇异终端滑模控制策略，在解决了奇异性问题的同时也保证了系统的有限时间稳定，取得了良好的控制效果。为进一步加强有限时间控制效果，文献[14]提出了一种快速非奇异终端滑模控制策略，该方法相比于前述控制策略具有更高的控制精度及更快的收敛速度，其控制效果更佳。

本文针对在复杂未知环境下的四旋翼编队跟踪控制问题，设计一种基于有限时间扩张状态观测器的主从编队控制方法(FTESO-LFFC)。对于领航者子系统，提出一种ISM控制策略，通过引入的积分项，消除了传统滑模控制中的趋近阶段，提高了系统的鲁棒性。对于跟随者子系统，提出一种NTSM控制策略，通过引入的超扭趋近律削弱了抖振情况。对于四旋翼系统所受的外界扰动，引入FTESO实现了对于扰动的有限时间观测，以上所设计的控制策略均具有有限时间收敛特性，其收敛速度更快、控制精度更高。最终，稳定性分析证明了闭环系统的有限时间稳定性。

1 预备知识及问题描述

1.1 预备知识

引理1[15]存在如下系统:

(1)

引理2[16]存在如下系统:

(2)

式中:ζ1、ζ2为系统状态；1、2、φ1、φ2均为正常数；若满足则该系统是有限时间稳定的。

引理3[17]存在如下非线性系统:

x(t)=f(x(t))

(3)

式中:x=[x1,x2,…,xn]T为系统状态；f(·)是在原点邻域上的非线性函数。如果存在一个正定标量函数V(x)满足如下条件:

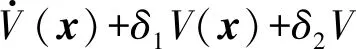
(4)

式中:δ1>0;δ2>0;0<ϑ<1;则该系统是有限时间稳定的。

1.2 问题描述

令Ξn=[zn,xn,yn]T表示地理坐标(OE,XE,YE,ZE)下四旋翼进行垂直与平移运动的位置信息，Γn=[φn,θn,ψn]T表示机体坐标系(OB,XB,YB,ZB)下四旋翼进行旋转运动的横滚角、俯仰角和偏航角信息，其中下标n=0,1,2分别代表领航者与两个跟随者四旋翼，基于文献[11]，可得如下的四旋翼动力学模型:

(5)

式中:c(·)与s(·)分别代表cos(·)与sin(·)函数；a1=(Iy-Iz)/Ix;a2=Jr/Ix;a3=(Iz-Ix)/Iy;a4=-Jr/Iy;a5=(Ix-Iy)/Iz;b1=Iq/Ix;b2=Iq/Iy;b3=1/Iz;m为四旋翼的质量;Iq为四旋翼质心与旋翼之间的距离;Ix、Iy、Iz和Jr分别表示机体的转动惯量与旋翼的转动惯量;d1n至d6n表示四旋翼飞行过程中所受的外界扰动;ω1n至ω4n表示四旋翼四个电机的旋转速度且它们之间的关系为ωn=ω1n-ω2n+ω3n-ω4n;u1n、u4n、u5n、u6n为四旋翼的四个控制输入。

由于四旋翼是一个具有四输入六输出的欠驱动系统，因其无法控制所有的状态，所以令zn、xn、yn和ψn跟踪期望轨迹znd、xnd、ynd和ψnd同时引入两个虚拟控制变量u2n和u3n来表示俯仰角、横滚角与机体沿x轴及y轴运动之间的关系，具体形式如下:

(6)

对式(6)进行反解运算可得横滚角和俯仰角信息的期望值，即:

(7)

进一步简化x与y通道的动力学模型，得到：

(8)

如图1所示，基于一领航者、两跟随者的编队结构，领航者与跟随者的相对距离关系可表示为:

图1 xy平面下的领航者-跟随者编队结构

(9)

式中:Ixn、Iyn(n=1,2)是跟随者1和跟随者2与领航者的相对距离ln在x轴和y轴上的投影。v0、vn与vx0、vxn、vy0和vyn分别为领航者与跟随者1、跟随者2的线速度及其分量，由式(9)得：

(10)

式中:lxnd、lynd为领航者与跟随者的期望相对距离，xnd、ynd是在领航者位置信息已知情况下根据相对距离关系解算出来的跟随者平移运动的期望位置信息。

(11)

式中:fin,gin,i=1,2,…,6为其对应的非线性函数。

考虑四旋翼的轨迹跟踪误差系统如下:

ein=x1ind-x1in

(12)

式中:x1i0d=(z0d,x0d,y0d,φ0d,θ0d,ψ0d),x1ind=(znd,xnd,ynd,φnd,θnd,ψnd)为领航者与跟随者的期望轨迹。

本文的控制目标是，考虑一组受外界扰动影响的四旋翼系统，对于领航者，基于给定的期望轨迹z0d、x0d、y0d、ψ0d，通过设计有限时间控制律ui0使得跟踪误差ei0在有限时间内收敛到零。对于跟随者，将领航者的高度z0、偏航角ψ0，以及基于领航者位置信息解算出的xnd、ynd作为跟随者的期望轨迹，通过设计有限时间控制律uin使得跟踪误差ein在有限时间内收敛到零。对于外界扰动，设计有限时间扩张状态观测器实现对于扰动的有限时间观测。

假设1扰动din满足连续可微且有界，即:

(13)

式中:L是有界正常数。

2 FTESO-LFFC控制策略设计

本文提出一种基于有限时间扩张状态观测器的四旋翼主从编队控制策略，主要分为扰动观测器的设计，领航者子系统与跟随者子系统控制器设计，具体设计方案如下。

2.1 有限时间扩张状态观测器

考虑式(11)，一种有限时间扩张状态观测器可以设计为如下形式:

(14)

式中:z1in、z2in、z3in分别为x1in、x2in、din的观测值；β1>0,β2>0,β3>0为所设计的正常数。这里sig函数具体表示为:

sigα(x)=|x|αsign(x)

(15)

2.2 领航者子系统控制器设计

结合式(11)与式(12)，领航者的轨迹跟踪误差可表示为：

ei0=x1i0d-x1i0

(16)

误差变量的一阶导数形式为:

(17)

结合式(16)和式(17)，一种积分滑模面设计如下:

(18)

式中:ci>0，ki>0为所设计的正常数。

考虑假设1及式(16)-式(18)，积分滑模控律设计如下:

fi0-z3i0+kiei0)

(19)

式中:hi>0，ηi>0，t>0，κ>0为所设计的正常数。

2.3 跟随者子系统控制器设计

同理可得跟随者的轨迹跟踪误差及其导数为:

ein=x1ind-x1in

(20)

(21)

结合式(20)和式(21)，一种非奇异终端滑模面设计如下:

(22)

式中:λ>0;p和q是正奇数，且1

基于假设1及式(20)-式(22)，设计如下的非奇异终端滑模控制律:

(23)

式中:ρ1i>0,ρ2i>0，为所设计的正常数。

3 稳定性分析

定理1FTESO-LFFC考虑满足假设1的式(11)，在式(14)、式(19)、式(23)的作用下，系统所受的扰动可在有限时间内被观测到，同时式(16)、式(20)中的跟踪误差ei0、ein，可以在有限时间内收敛到零，其实际状态可以在有限时间内跟踪上期望值。

证明:证明过程分为三步，首先证明扰动din可以由式(14)实现有限时间观测，其次证明领航者的跟踪误差ei0可以在有限时间内收敛到零。最后证明跟随者的跟踪误差ein同样可以在有限时间内收敛到零。

步骤1定义扰动观测误差如式(24)所示。

(24)

结合式(11)和式(14)，对式(24)求导得:

(25)

由引理1可知，式(14)对应系统可以实现有限时间稳定，同时观测误差μ1in、μ2in、μ3in可以在有限时间内收敛到零，即:

z1in≡x1in,z2in≡x2in,z3in≡din

(26)

进一步可得:

z3in-din=0

(27)

步骤2对于领航者子系统，建立如下的Lyapunov函数:

(28)

对式(28)求导可得:

(29)

将式(19)与式(27)代入式(29)中可得:

(30)

对整个领航者子系统，建立如下Lyapunov函数:

(31)

对式(31)求导得:

(32)

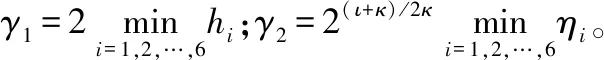
由引理2可知，领航者系统的跟踪误差ei0可以在有限时间内收敛到零。

步骤3对于跟随者子系统，对式(22)求导可得：

(33)

将式(23)与式(27)代入式(33)中可得：

(34)

(35)

对式(35)求导得:

(36)

由引理3可知，所设计的非奇异终端滑模面能够在有限时间内收敛到零，进一步，根据式(22)可知，跟随者的跟踪误差ein同样可以在有限时间内收敛到零。

根据以上分析可知，式(14)、式(16)-式(19)、式(20)-式(23)可以实现有限时间稳定，进一步来看，整个编队系统也可以实现有限时间稳定。

4 仿真研究

为了验证所提出控制策略的有效性与可行性，本文采用文献[11]中的四旋翼飞行器进行仿真研究，具体参数为m=2.2 kg,g=9.81 m/s2,lq=0.235 m,b=3.14×10-5m·s-2,d=7.6×10-7N·s-2,Ix=Iy=6.228×10-3kg·m-2,Iz=1.125×10-2kg·m-2,Jr=1.54×10-5kg·m2。

令领航者期望轨迹为(z0d,x0d,y0d,ψ0d)=(0.1t,sin(0.2t),cos(0.2t),0.1)。领航者与两个跟随者的初始位置为(0,-0.5,1)、(0,-1,2)和(0,-1,0)，同时其期望相对距离在两坐标轴的投影为lx1d=ly1d=1,lx2d=ly1d=-1。

假设领航者与两个跟随者在飞行过程中所受扰动为di0=cos(0.5t),di1=sin(0.5t),di2=cos(0.5t)+sin(0.5t),i=1,2,…,6。同时，其控制器与观测器的参数选择为c1=c2=c3=10，c4=c5=c6=60,ki=1,hi=1,ηi=1,ρ1i=30,ρ2i=1,i=1,2,…,6,ι=1,κ=2,λ1=λ2=λ3=1,λ4=λ5=λ6=10,p=7,q=5,β1=β2=β3=10。

仿真结果如图2-图10所示。图2-图3给出了领航者与跟随者1、跟随者2的轨迹跟踪情况与姿态角变化曲线，可以看到领航者与跟随者都可以在较短时间内跟踪上其对应的期望状态，具体来看，两者实际的位置与偏航角曲线在5 s内就可以稳定地跟踪期望值，但受四旋翼固有欠驱动特性的影响，横滚角与俯仰角跟踪较慢，但在10 s内也可以达到稳定。为了突出本文所设计控制策略的优越性，引入传统的滑模控制(SMC)策略进行对比仿真研究，由图2和图3可以看出，在存在外界扰动的情况下，本文所设计控制策略稳定性更强，而传统的滑模控制策略无法保证稳定的轨迹跟踪效果。在实现上述轨迹跟踪控制的基础上，进一步对外界扰动进行了观测，图4-图9给出了领航者与跟随者所受扰动及其观测值的情况，可以看到所设计的扰动观测器具有良好的观测效果，可以在短时间内跟踪上实际的扰动。如图10所示是编队系统的空间轨迹跟踪效果图，可看出相比于传统的滑模控制策略，本文所设计的控制策略与扰动观测器，可以实现快速、稳定的编队跟踪控制效果。

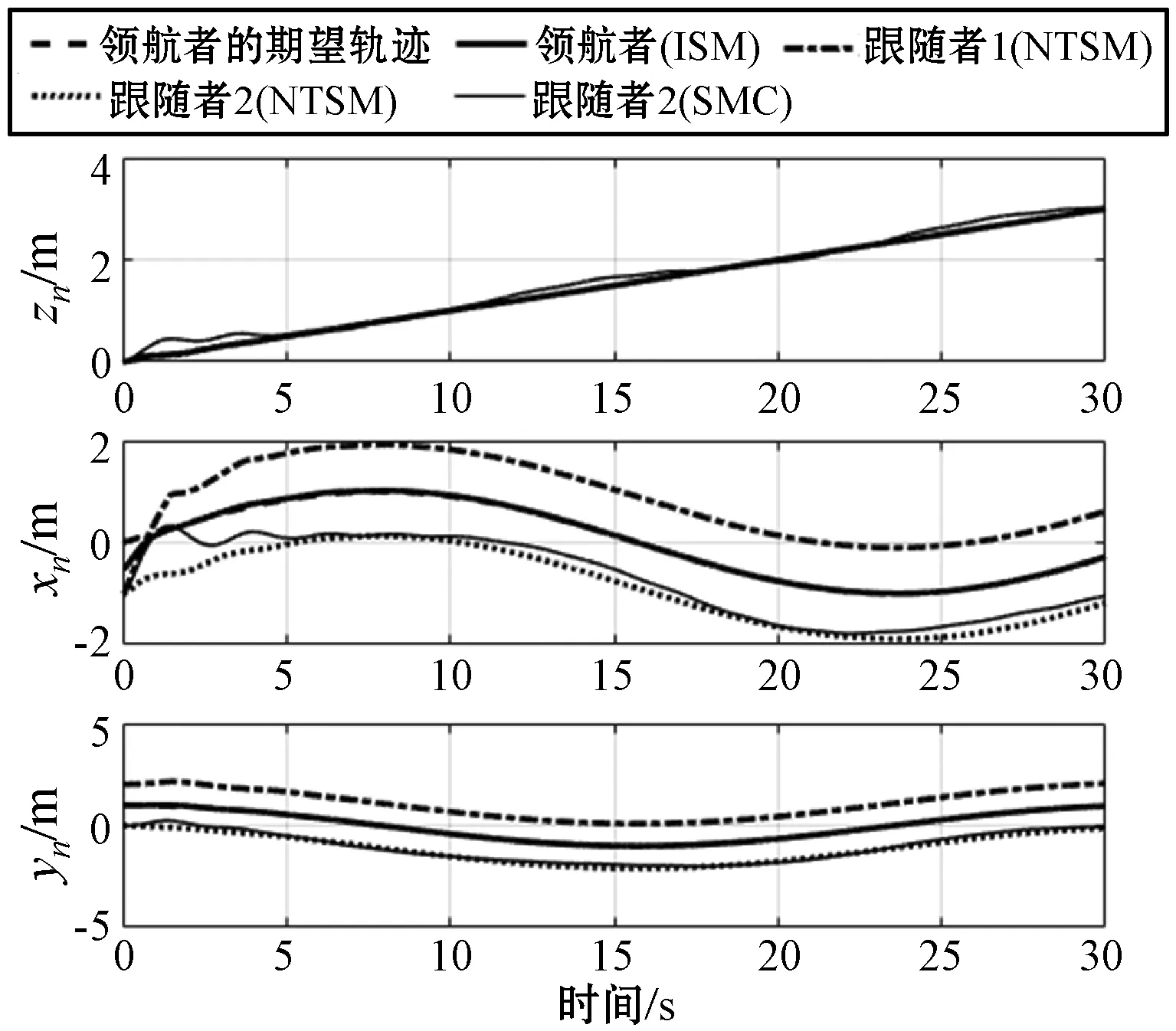
图2 领航者与跟随者的位置跟踪曲线

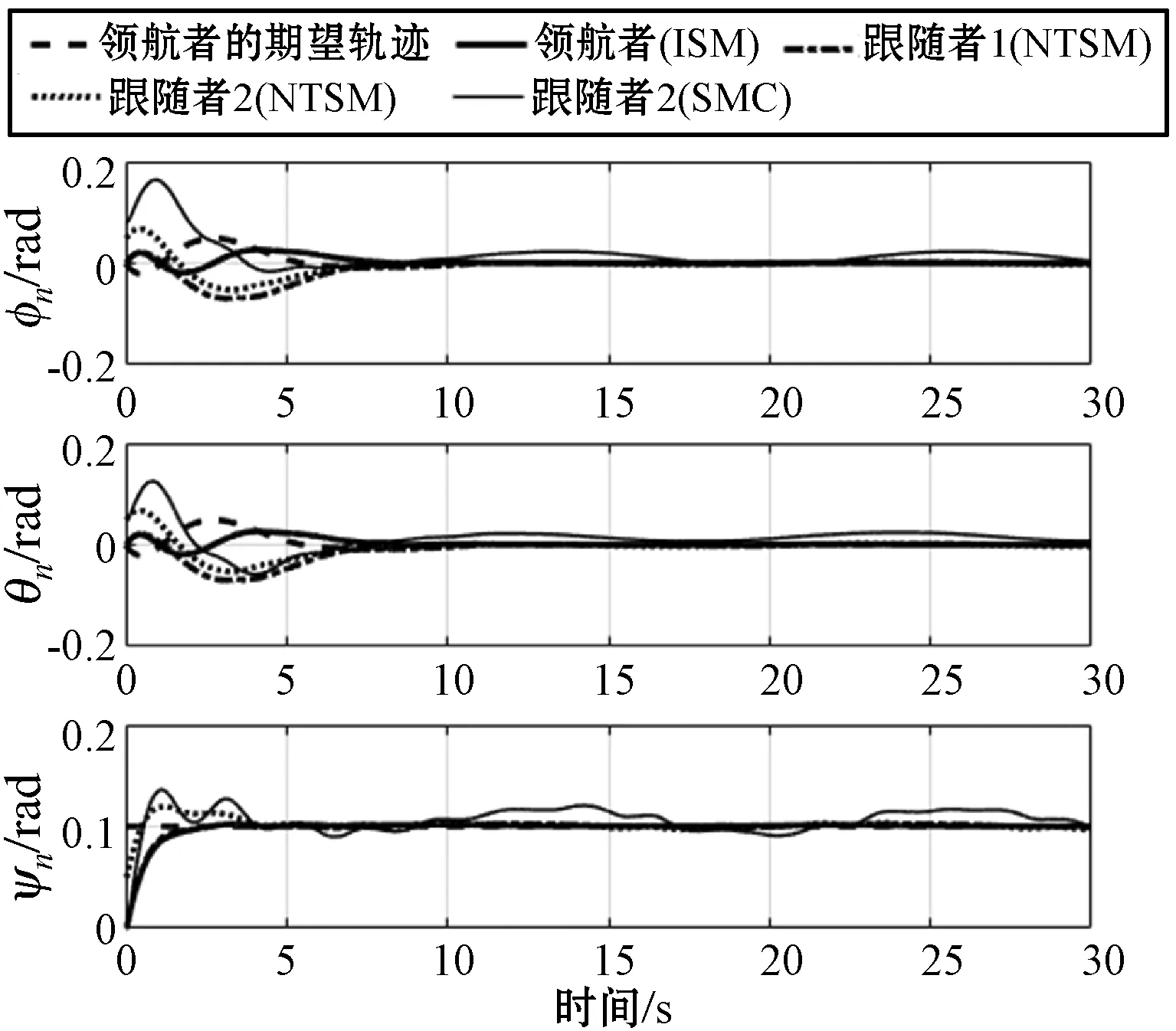
图3 领航者与跟随者的姿态跟踪曲线

图4 领航者所受扰动d10至d30的观测情况

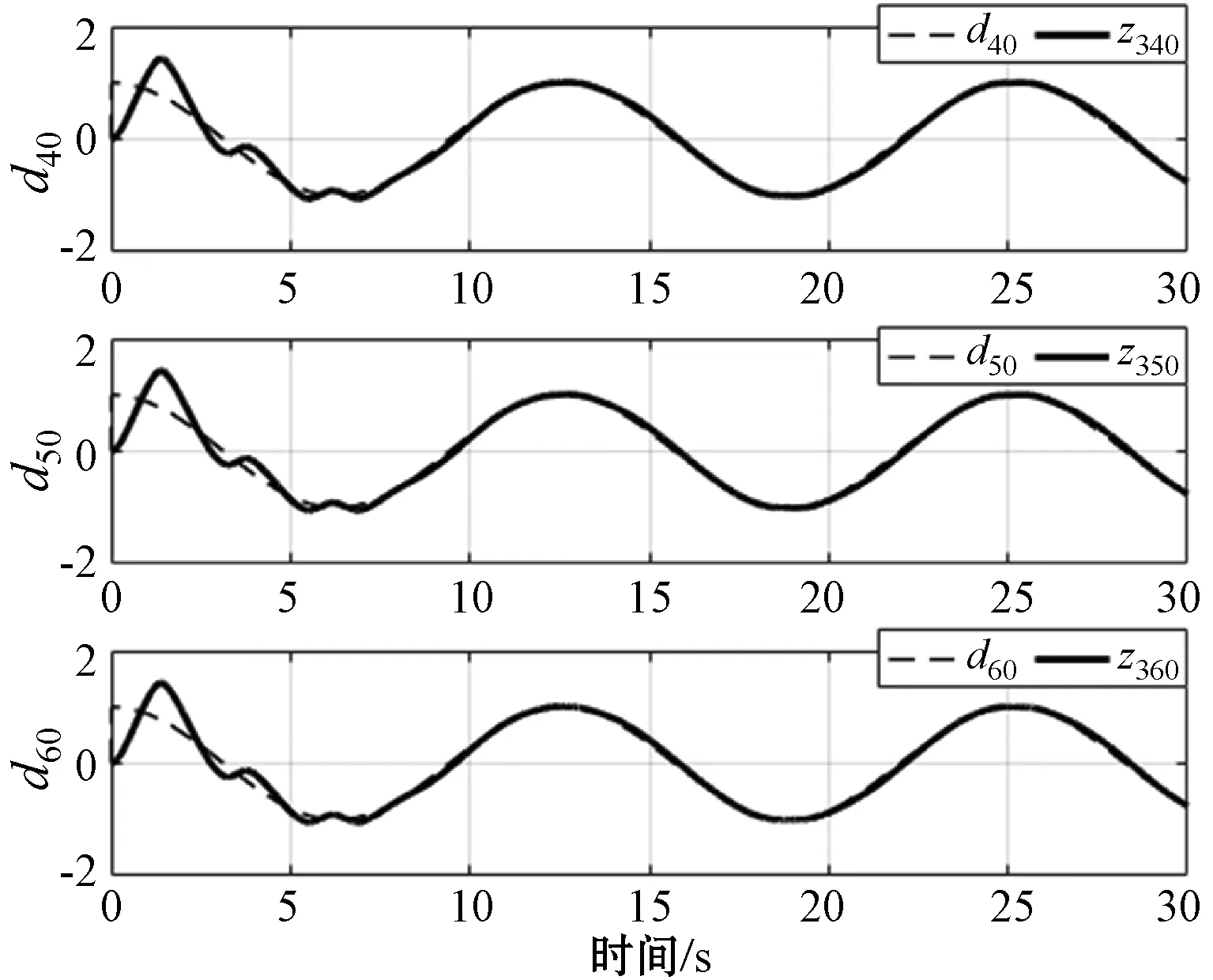
图5 领航者所受扰动d40至d60的观测情况

图6 跟随者1所受扰动d11至d31的观测情况

图7 跟随者1所受扰动d41至d61的观测情况

图8 跟随者2所受扰动d12至d32的观测情况

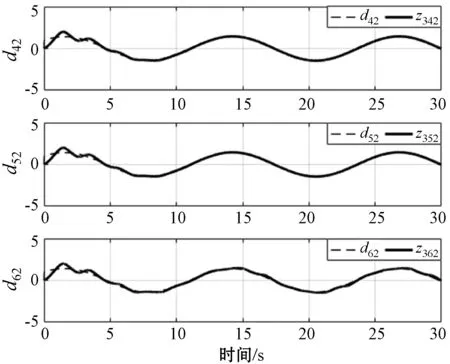
图9 跟随者2所受扰动d42至d62的观测情况

图10 编队飞行的三维轨迹跟踪效果图

5 结 语

本文提出一种基于有限时间扩张状态观测器的主从编队跟踪控制策略，实现了四旋翼编队在外界干扰下的快速、稳定的轨迹跟踪控制。该方法采用有限时间扩张状态观测器实现了有限时间内对系统扰动的观测，提高了系统的抗干扰能力。同时对于整个编队系统，将其分为领航者与跟随者子系统，分别对其采用积分滑模与非奇异终端滑模控制策略，这两种方法均具有有限时间收敛特性，相比于传统的渐进稳定控制策略，所得到的有限时间稳定使得闭环系统的控制精度更高、收敛速度更快。仿真实验验证了所提出控制策略的可行性与有效性。