GGb软件与高三数学教学的深度融合
刘健康


【摘要】GeoGebra(简称GGb),作为功能强大的数学制图工具,具有动态、可视化的特点,能够很好地将高中数学中比较抽象、空间思维强的知识点以一种真实的情景再现。动态的过程演变,可变化的形式展现,可以激发学生的学习兴趣,快速理解数学的本质。目前,GGb在我国得到广泛的运用和推广。本文根据高三数学教学的积累,从几个实例阐述GGb在高三数学教学上的应用,提高教学效率。
【关键词】GGb;高三数学;数学教学
信息技术与学科教学的融合,是改变传统教学模式的重要举措。目前的教学中,部分老师对教育信息化发展的重要性存在认识不足,个别老师还坚持“粉笔+教材”的传统模式,有的老师只会点击教辅的PPT,不做改动和选择,有的条件好的学校提供希沃白板设备,老师也就只是用来代替粉笔书写。这些缺乏主动意识的行为,导致课堂质量、效率及效果较低。随着国家“双减”政策的实施,提高课堂教学效率、效果势在必行。
GGb是一个动态几何软件。教师可以通过操作GGB 的滑动条、动点、制作动画让学生感受数学动态的过程,在掌握数学知识的过程中体会数形结合的乐趣。利用GGB 使学生经历数学知识的发生以及问题的发现、提出、分析以及解决的过程。利用3D 绘图区,增加立体几何教学的直观性,降低抽象难度,减少学生学习过程中的障碍,增加学生的学习兴趣,激发抽象思维的同时减少学生学习的畏难情绪。
一、GGb软件在高三数学概念教学中的应用
在高三教学中,概念复习教学特别重要,教师应该从多角度充分揭示概念的内涵和外延,引导学生对概念进行本质的理解和提升。众所周知,三角函数线这个概念是个教学难点,学生普遍感觉困难,新教材也意识到这一点。其实三角函数线就是三角函数的几何特征,体现了数学中代数与几何的交汇,有数形结合的思想运用。有了GGb,我们可以结合动态展现,根据学生已学向量知识,更清晰掌握这个概念。
第一,设计意图:角α的正弦值,余弦值,正切值都是“数”,而对应正弦线、余弦线、正切线都是“形”。通过 GGb 的动态呈现,步步有据,形象直观,可以得到结论:任意角α的三角函数线就是对应的向量,这些向量的数值就是对应的角α的三角函数值。
第二,技术操作。如图1所示:(1)用画圆工具做出单位圆;(2)用描点工具在单位圆上任取点B;(3)用直线工具做出射线OD,向量CB,OC,DG;(4)点击B点属性,开启动画。
图1
第三,操作点评。制图时要注意角α旋转到第二、三象限时,正切线是反向延长的相交。让学生密切注意动点所在的位置。对每一个象限的特征加以区别,让学生通过观察后,主动描述三角函数线的概念。
通过以上的教学过程,将数学概念动态化、直观化,有效帮助学生理解概念本质,有利于培养学生的直觉思维能力和主动探究意识。通过促进学生形象思维的培养,进一步发展逻辑思维。
二、GGb 软件在高三数学立体幾何教学中的应用
在高三教学中,立体几何一直是高考的重点。需要培养学生的空间想象能力,掌握空间里点、线、面的原理,表达和位置关系,熟悉柱体、锥体、台体和更多组合几何体的结构,还需要从坐标代数的角度进行各种距离、角度的计算,同时探索动态情况下的最值变化。学生空间思维能力不足,平面与空间的转换方面有困难,学生如果不能够正确理解立体几何各定理,不能梳理好他们之间的关系,会导致学生思维受局限,不能正确全面认识立体图形,就无法做出正确的证明和计算。以例1的教学为例。
例1:已知P,A,B,C,D是球O上的五个点,在四边形ABCD中,AD//BC,AB=DC=AD=2,DC=PA=4,PA⊥面ABCD。求球O的体积。
学情分析:底面是等腰梯形,需要底面外接圆,部分学生无法正确作出,不能判断圆心位置,大部分学生没有寻找球心位置的正确方向,不会用球心和圆心的连线垂直外接圆面的关系。
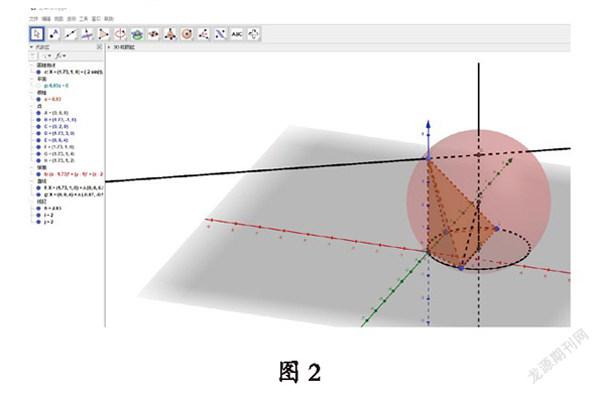
解决办法:用GGb画出底面外接圆,让学生体会外接圆圆心的位置,引导学生证明圆心是BC的中点,再用GGb找出球心位置,让学生充分认识立体结构、线面关系,找到计算球半径的三角形。
技术操作:如图2所示:(1)在3D绘图区用描点工具找到五个点,用锥体工具连成棱锥;(2)用作圆工具点击A,B,C三点做出外接圆,确定圆心;(3)用垂线工具点击圆心,外接圆面,作出垂线,再过P点做刚才垂线的垂线;(4)用中点工具确定球心,用多边形工具连接球心,圆心,球面上点,连成三角形;(5)三角形中的计算球半径。
操作点评:在用GGb 展示知识重难点的同时,还要注意课件中的颜色搭配以及信息布局,让学生可以一眼就抓住课件中所要呈现的重要信息,形成记忆点。其次,还可以通过GGb的复原、重复、隐藏、显示、拖动和动画,配合生动有趣的语言对学生进行教学、反馈和探索。教学中,应把学生的直观感受摆在重要位置,充分调动学生的感觉器官,让学生能够将自己的直观感受作为出发点,概括出现象的本质及其规律。
三、GGb 软件在高三数学综合能力教学中的应用
新课标提出数学六大核心素养:数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析。其中,培养学生空间想象能力,发展形象思维、抽象思维是中学数学教学的重要内容。《高中数学新课程标准》《全日制义务教育数学课程标准》中提到注重信息技术和数学课程的有机整合,课堂上要尽可能使用多媒体设备、教学工具等,将抽象的数学问题直观展现,营造轻松愉悦的多媒体教学环境,引导学生发现问题、提出问题、分析问题、解决问题,提高空间想象能力。以例2的教学为例。
例2:已知M为函数y=8/x 的图像上任意一点,过M作直线MA,MB分别与圆x+y=1相切于A,B两点,则原点O到直线AB的距离最大值为( )。
A.1/8 B.1/4 C. 根号2/2 D.根号2/24
学情分析:学生会习惯设M(x,y),做出圆的两条切线后,不能准确求出直线AB的方程,从而用点到直线的距离公式解决不了问题。或者会没有根据去猜测动点M的位置。
解决办法:用GGb做出动态图,在变化过程中显示原点O到直线AB的距离的变化状态和规律,体会M点的特殊位置,激发探索的兴趣。教师再从代数和几何两方面培养学生的综合能力,第一,用代数变换学习切点弦的求法,再用点到直线的距离公式,最后结合基本不等式知识。第二,从几何角度,发现直角三角形中的射影定理,得到点到直线的距离和OM长度的关系,利用M点在曲线上,基本不等式求出最值。
技术操作:如图3所示:(1)用画图工具做出单位圆;(2)直接输入函数y=8/x,可以立即显示曲线图像;(3)用描点工具在y=8/x图像上任取点M;(4)用作切线工具,点击点M和圆O可作两条切线;(5)用直线工具做出各条线段,标明垂直90度;(6)点击点M的属性,开启动画(也可以用滑动杆控制或者复选框)。
操作点评:GGb软件的视图工具、操作过程的功能,能够体现数学思维过程,活跃课堂氛围、提高学生参与度,但是课堂教学最后还是以学生为主体,信息技术是辅助手段,融合得很好,恰当的设计会效果显著。演示的同时,教师要注意及时引导和归纳,最后形成知识点的传授,培养学生的数学综合能力。
四、GGb 软件在高三数学教学中的应用意义和展望
多元表征理论提出:信息、资源(如数学概念或数学问题)通过建构心像码,担任“桥梁”角色,对信息进行编码和形成多种转译方式,从而呈现对信息的多元化的表征。高三数学教学是多个模块知识点的综合复习,可以用文字语言、符号语言以及图像来表征,这样通过多种表征方式能够促进学习者深刻理解增函数概念的本质,有利于培养学习者学会多角度、多方位、多种思路解决问题的习惯,在学习学科知识的同时,也可以进行美育的间接培养。
可视化技术通过将抽象的、复杂的知识或信息利用直观的图像或图形呈现出来,以帮助学生快速地理解内容、发现规律、交流信息。高三数学可视化教学就是将抽象的数学学习对象(概念原理、结构关系、思想方法等)用可看见的表征形式(图形、图像、动画等)清楚直白地呈现出来,使学生对数学学习对象有一个形象、直观、整体的认识和理解。
最新的人教A版和人教B版高中数学教材中,以GGb软件为载体,介绍了如何利用计算机技术实现数学功能,并开展相应的教学活动。所以教师需要主动学习,通过论文、书籍、丰富的在线资源学习,还可以通过社交群体、区域教研、公开课等方式进一步学习GGb,各级教育部门非常重视,一批优秀老师通过实践取得了很好的成绩,各种培训推广活动颇有成效。在高三数学教学中,平面几何、函数、三角、立体几何、解析几何与GGb软件的融合应用比较多,在概率统计上相对不足。同时我们还需要注意现在的学生本身GGb知识不足够,而且暂时作为主体的参与度不高,学生只是感官上观察、体会,所以在课堂教学中,我们不能唯“技术论”,用好GGb软件这个辅助,全方位去提高课堂效率。
综上所述,高三数学就是几何、代数的组合体。在高三数学的学习当中,数形结合思想是学习数学的主要思想。GGb软件帮助数学教师丰富教学方法,通过有效的教学促进学生对数学本质的理解。应用GGB软件辅助高三數学教学,可以降低学习数学的难度,有利于培养学生的学习兴趣,激发求知欲,给数学教学改革注入了新的活力。
参考文献:
[1] 项俊.GGb软件在高中数学教学中的应用探究[J] .上海中学数学,2019(4):25-27.
[2] 彭淑琴.基于GGb的中学数学可视化研究[J] .陕西理工大学,2020.
[3] 刘怡轩.GGb在中学数学教学中的应用与展望[J] .中学数学教学参考,2021(5).
3201501908274

