侵彻爆破弹对机场跑道毁伤效果仿真*

曾松林 韩玉龙 孙守福 陈 榕

（海军航空大学航空作战勤务学院 烟台 264001）

1 引言

打击破坏敌机场跑道，阻止敌飞机起飞作战，是取得战争主动权、赢得战争胜利的一种有效手段。

国内外许多学者对机场跑道的毁伤评估方面做了许多有益研究。张臻等研究了打击机场跑道的瞄准点选择方法，设计了一种基于最小起降窗口的打击瞄准点选择算法，并利用Monte-Carlo方法计算了封锁概率［1］。曾涛等研究了使用战术导弹打击机场跑道的毁伤概率，分析了战术导弹母弹的落点规律和子弹散布规律，瞄准点的选择方法，并进行了毁伤概率计算，基于最小起降窗口概念，实现了给定机场目标和毁伤等级要求下导弹型号的最优选择，最小导弹消耗预测［2］。李勇等研究了面向效果的机场跑道打击方案，对压制机场跑道作战过程进行建模，构建机场跑道打击方案评估模型［3］；韦常柱等研究了布撒器对机场跑道的封锁方式，以概率积分的方法分析开舱点位置偏差时，布撒器对机场跑道的封锁概率［4］；毛亮等研究单发机载布撒器对机场跑道封锁效率，建立了低空抛撒带伞子弹药质点弹道方程组与仿真计算模型，采用Monte-Carlo方法进行了仿真计算［5］；朱涛等研究了基于粒子群算法的机场跑道打击效果评估方法，在已知跑道长宽、弹坑分布和最小起降区长宽的条件下，快速搜索跑道上的最小起降区［6］；王刚等研究了远程制导火箭子母弹对机场跑道毁伤研究问题，采用Monte-Carlo方法对远程制导火箭子母弹打击机场跑道的炸点分布进行仿真模拟，计算了相关战技术因素对机场跑道毁伤的影响程度［7］；鞠勇研究了子母弹打击机场跑道散布规律与毁伤效果，建立了子母弹的飞行动力学模型，计算了具有不同特性的母弹弹道，给出了子弹散布特征范围的具体计算方法［8］；袁寅辉研究了基于多属性决策理论的子母弹打击机场跑道综合评价模型，建立了子母弹打击机场跑道的综合评价模型，研究了子母弹打击机场跑道的具体过程，提出了可行的定量评价方法［9］。

目前，综合考虑弹药性能参数、投放条件、机场跑道结构特性、材质等因素来研究对机场跑道毁伤评估的方法在文献中没有体现。基于此，文章以侵彻爆破弹打机场跑道为例，对炸弹从投放到弹目交会之前的运动过程进行物理建模，计算得到炸弹的弹着角、末速等；然后结合机场跑道的结构特性、材质计算炸弹的穿入厚度、等效弹坑容积，支撑机场封锁概率计算。

2 炸弹线性阻力模型

文献［10］给出了计算炸弹在空中运动时空气阻力加速度的仿真算法，该算法充分考虑影响炸弹空气阻力加速度的各种因素，因而算法精度高，但编程较复杂、工作量大。为简化编程，同时保证计算精度在允许范围内，本文采用文献［11］的炸弹弹道模型。假设炸弹所受的阻力与速度成正比，炸弹下落过程中受力分析如图1所示。

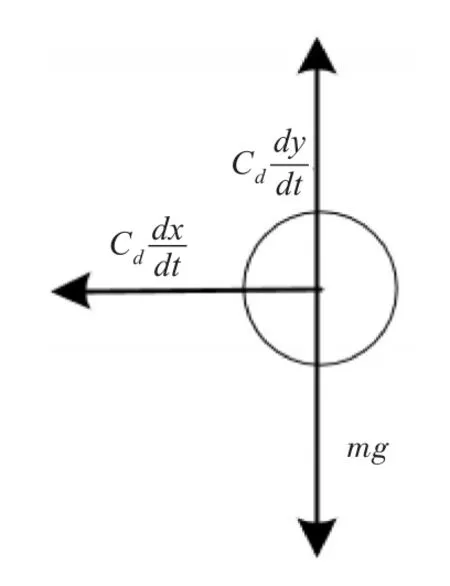
图1 炸弹投放后受力分析

2.1 垂直运动

在垂直方向上：

cd为阻力系数；vv为垂直速度。

对式（1）积分得到：

从投放位置开始的垂直位移：

其中：y为下落高度。

2.2 水平运动

仿真计算表明，采用线性阻力模型，无论是高阻还是低阻炸弹，模型给出的结果都在最高精度模型的5%之内。

3 侵彻爆破弹对跑道的毁伤作用

侵彻爆破弹对机场跑道的毁伤作用，主要包括侵彻和爆破两种。

3.1 侵彻作用

3.1.1 单层固体介质的穿入厚度

2) 墙体水平位移时程曲线：在此选择三个有代表性的墙体水平位移监测点ZQT-01、ZQT-03、ZQT-23随着土方开挖的变形时程曲线进行分析，三个测点的变形时程曲线见图3～图5。

炸弹以一定弹着角穿入混凝土等介质时，头部下端先侵入，产生一个向上的抬头力矩，使侵入介质后的弹道向上弯曲［12～15］。炸弹的穿入行程，即穿入距离L穿入为

L穿入为穿入距离；K穿入为介质的穿入系数；m为弹药的质量；d为弹药的直径；V末为弹药的末速；H为弹头部长度；λ为弹径修正系数；λ1为弹型修正系数。

炸弹穿入混凝土等介质后，弹头顶到地面的距离为穿入厚度，穿入厚度为

对于高（中）阻弹：

对于低阻弹：

3.1.2 多层固体介质的穿入厚度

机场跑道由多层介质构成，需要分别计算炸弹在每层介质中的穿入厚度，直到炸弹在该层的穿入厚度小于该层介质厚度为止。计算过程如下［16］：

b穿入i为由第i层上一层的剩余穿入厚度换算成对i层的穿入厚度；b穿入i-1为对第i层上一层穿入厚度；li-1为i层上一层的厚度（用公式第一次运算时，li-1即为l1）；l1、l2为第一层、第二层介质的厚度；K穿入i为第i层的阻力系数；K穿入i-1为第i-1层的阻力系数。

3.2 爆破作用

当战斗部穿入介质一定深度爆炸，形成弹坑。要先按前面的公式计算多层介质中的穿入厚度，再按下述公式计算在多层介质中的综合深度修正系数 m′。

判别：

外爆时：

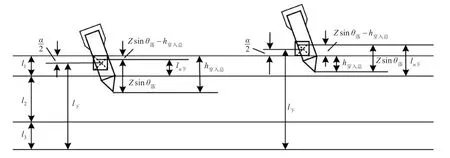
图2 装药中心位置与深浅比的关系

m为深度修正系数；Z为装药中心至弹头的距离；la下为装药中心所在层以下的厚度；l1为第一层介质的厚度。

内爆时，弹头穿至装药中心所在层：

b穿入a为第a层介质的穿入厚度；la为装药中心所在层厚度；la上为装药中心所在层以上的厚度；la下为装药中心所在层以下的厚度。

弹头穿至装药中心所在层的下一层：

K毁1为第1层介质的毁伤系数；K毁a为装药中心所在层介质的毁伤系数；K毁a-1为装药中心所在层上一层介质的毁伤系数；K毁n为第n层（最下层）介质的毁伤系数；K毁n-1为倒数第2层介质毁伤系数；P′为综合深度比；m′为综合深度修正系数；为相当于a层的装药中心深度；R毁全a装药中心所在层介质完全填塞条件下的毁伤半径。

再按下面公式计算得到对最小层的毁伤半径R毁n及爆破孔直径D平。

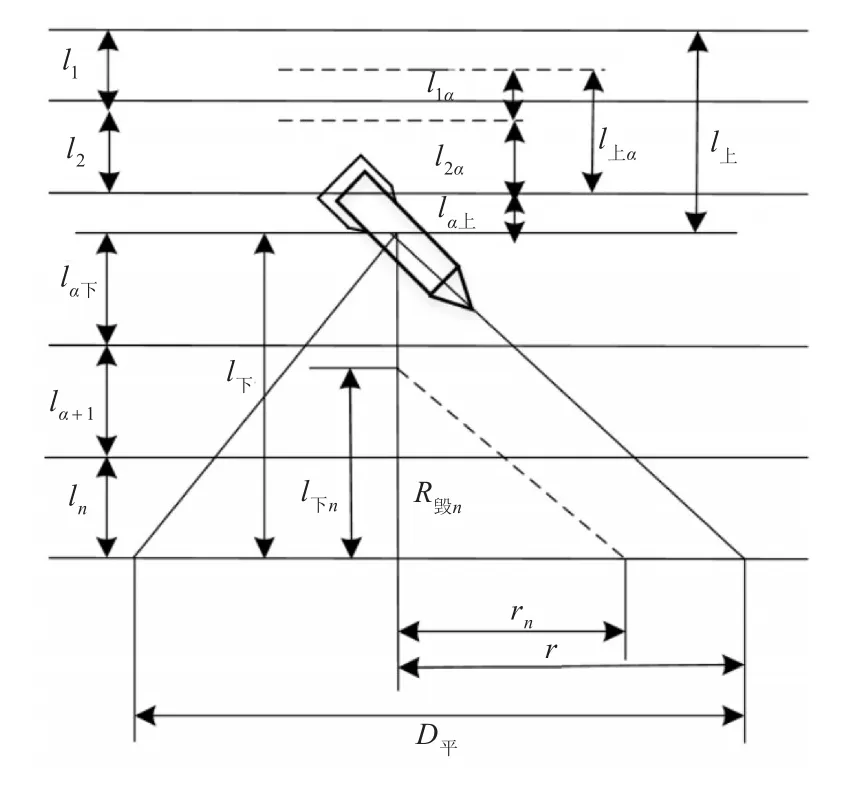
图3 多层介质工事顶的爆破孔

l下为装药中心以下各层介质的总厚度；D平为在最下层介质的爆破孔直径。

为了方便计算，弹坑容积简化为一个球体。

3.3 仿真计算流程

流程图如图4所示。

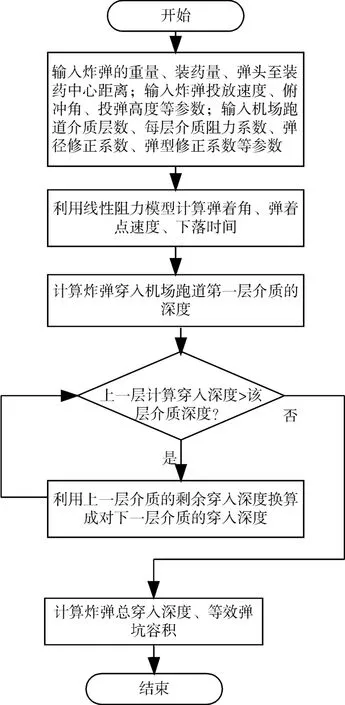
图4 炸弹总穿入厚度及弹坑容积计算流程图

4 算例

某飞机使用一枚制导炸弹对机场跑道进行打击，投弹高度为1500m、水平投放速度为300m/s、水平阻力系数为0.05、弹径修正系数1.176、弹型修正系数1.437、弹药直径0.4m，介质依次有水泥混凝土—基层—土层；穿入系数分别为 0.9e-6、0.45e-6、9e-6；毁伤系数分别为 0.29、0.55、0.69；厚度为 0.4m、0.3m、2m；弹药重量为500kg、装药的当量为450kg、弹头至装药中心距离为0.6m、运用Matlab进行仿真。

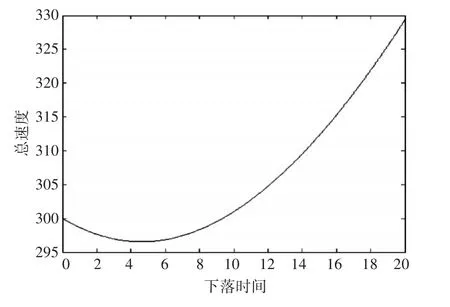
图5 炸弹总速度

从图6中可看出，投放高度从低空逐渐增高时，弹坑容积逐渐增大；到一定高度时为最大值；此后，投放高度继续增高，使炸弹穿入介质过深，弹坑容积反而减小（只是弹坑深度增加）；大量级的炸弹因穿入能力强，在中、高空投下时可能因穿入介质过深而形成隐弹坑。此仿真计算结果与炸弹在靶场的试验结果较为吻合。

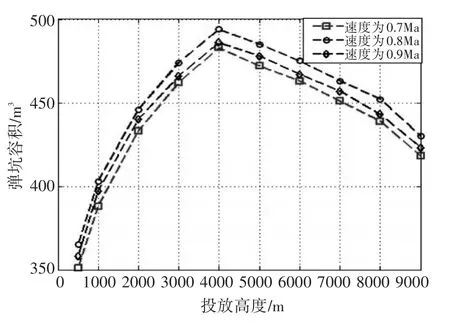
图6 不同高度速度投弹时弹坑体积/m3

5 结语

文章以飞机投放侵彻爆破弹打击机场跑道为例，对其毁伤效果计算方法进行了深入研究。给出了炸弹在空中和侵入机场跑道内部的运动过程的计算步骤，并进行了仿真计算。结果表明：该方法具有一定的实用参考价值。