二维蜂窝五模材料的能带特性与品质因子分析*

巫继航 韩邦熠

（海军工程大学舰船与海洋学院 武汉 430030）

1 引言

五模超材料是一种退化的固体弹性介质，由美国犹他大学的Milton与Cherkaev［1］最早提出。传统固体材料的弹性矩阵对应有6个特征值和相应的6个特征向量，分别对应材料的每一种形变模态。如果某个特征值表达为零，则这个模式下的应力将使材料发生类似液体的流动。五模材料就是一种仅保留一个非零特征值的特殊固体材料，它包含5个易变形模态，只能承受与非零特征值对应的特征应力成比例的应力模式，从而解除了剪切与形变的耦合，呈现出“固体水”的特性。通过微结构的设计，五模材料的模量与密度可以根据实际应用需求进行调节，在舰艇的声呐透声窗与吸声隔振器件的选材具有长足的应用前景。

2008 年，Norris［2］率先将变换声学理论引入超材料的概念，提出了借助模量与密度各向异性材料实现声波调控的构想。Kadic［3～5］设计并制作了经典双锥构型的三维五模结构，并对其弹性模量进行了测定。Layman［6］等对双锥构型的几何参数进行优化，在细杆连接处增加球型配重以提升结构稳定性，同时设定倾斜角，以期定制地产生各向异性。Schuittny［7］等在此基础上利用侵入式激光微刻技术制备了小尺寸三维双锥型五模结构，并分析了连结直径和晶格常数的组合，指出满足声学性能的最佳设计结构体积模量与剪切模量之比应为1000以上。在综合考虑三维结构的稳定性与加工难度等缺陷之后，Hladky-Hennion［8］等设计了金属基的二维蜂窝状五模结构，其宏观等效密度、体积模量与水十分近似。Cai［9］等研究了附加星形配重的蜂窝结构的力学性能，Chen［10］等对二维五模材料进行了理论分析，提出了基于二维结构的声隐身斗篷。Zhao［11］等采用电火花慢速线切割工艺制备了铝基二维五模结构块体，并通过实验验证了该模型与水具有良好的声学匹配性。

上述研究表明，二维蜂窝状五模材料具有机械性能好、可设计性强等优势。然而，现有的二维结构大多基于均质蜂窝构型［12～14］，通过改变薄壁结构的边长、厚度以及配重大小来模拟近似流体的模量和密度，对于周期结构固有的各向异性研究还较少。本文基于有限元仿真方法，针对现有的二维蜂窝状均质五模材料进行非对称性设计，分析各向异性对其能带特性与品质因子的影响，考察各向异性对于五模材料声学性能的优化效果。

2 二维蜂窝状五模材料的各向异性设计

理想五模材料要求其体积模量B与剪切模量G之比尽可能的大，从而表现出类似流体的耐压缩、易变形的特征，现引入无量纲数品质因子I定义二者的比值，以此作为五模材料声学性能的考量。目前主流的二维均质蜂窝五模材料的单胞结构如图1所示，由六边形薄壁框架附加圆形配重构成，前者实现较大的品质因子，后者提供与水近似的等效密度。

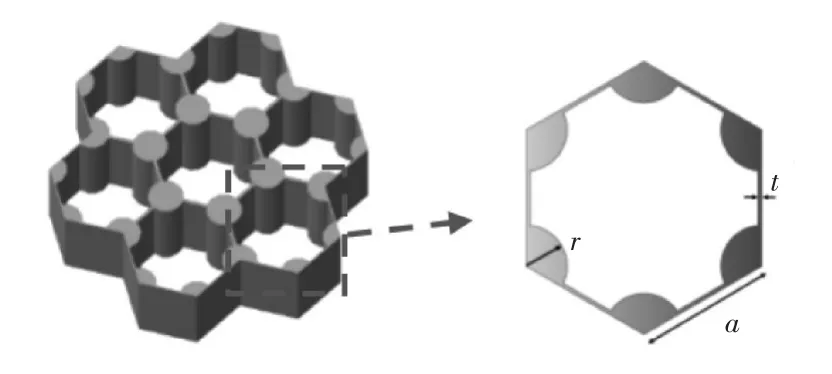
图1 二维均质蜂窝五模材料单胞结构

六边形蜂窝单胞的晶格常数为a，薄壁厚度与圆配重半径分别为t和r。为了使胞元能在x，y方向自由平移得到周期性结构，取图2（a）所示的框架结构作为基本平移单元，包括两个中心配重、四个半圆配重、一个中心薄壁、四个对角线薄壁以及四个半高半宽的边界薄壁。在此基础上，以两个中心配重P1、P2的位移和变形来构造二维各向异性的五模结构，本文采用以下三种较为直观的构造方式：1）令两个配重在y轴相对位移；2）令两个配重在x轴相对位移；3）等比例缩放两个配重的大小（假设对总密度不产生影响），分别记作模型α、模型β、模型γ，设计的原则是在不影响单胞的等效密度与框架基本构型的基础上，改变周期性排列使之产生各向异性，三种构造方式所对应的二维结构如图2（b）～（d）所示。

图2 基于二维均质结构的三种各向异性构建方式示意图

3 能带结构与品质因子

3.1 均质结构的等效模量和品质因子

研究五模超材料的声学性能一般通过分析其周期结构的频散曲线实现，不同振型对应的频散曲线绘制成的图谱被称为能带结构（Band structure）。以图1的二维均质蜂窝状五模结构为例，基材选取钛铝合金Ti-6Al-4V，其材料参数为密度ρ=4.40×103kg/m3，泊 松 比 ν=0.34，杨 氏 模 量 E=110GPa，Cl=6.10×103m/s，Ct=2.96×103m/s，其中，Cl表示材料的纵波波速，Ct表示材料的横波波速。蜂窝单胞的结构参数为a=0.01m，t=1.54×10-3m，r=2.94×10-3m。借助有限元仿真软件Comsol Multiphysics对其胞元附加布洛赫边界条件，并利用小波矢对不可约布里渊区进行扫掠，得到能带结构如图3所示。

横坐标为不可约布里渊区的边界，纵坐标为不同模态对应的特征频率，波矢量k取水平方向a/20。图3中灰色区域内，单胞只传递与波矢方向同向的模态，即只传输压缩波，抑制剪切波对振型的影响，因此被称为单模频带。其下边界（fl）与上边界（fu）的频率分别为18.43kHz与47.74kHz，记上下边界频率的差值与其平均值之比为频带的相对带宽，则单模频带的相对带宽为0.89。在这个频段内，由于固体结构激励的剪切波干扰被消除，五模材料表现出良好的水声匹配性，可用于声呐透声窗以及超声透镜等器件的选材设计。图3中黑色区域内没有任何特征频率表达，即压缩波和剪切波均被抑制，声波无法从结构中传出，因此被称为声子禁带（phononic forbidden band），该区域下边界与上边界的频率分别为67.93kHz与91.92kHz，相对带宽为0.30。在声子禁带频段内，理论上所有声波都无法通过，因而可以为吸声器材和声学屏蔽等领域提供参考。

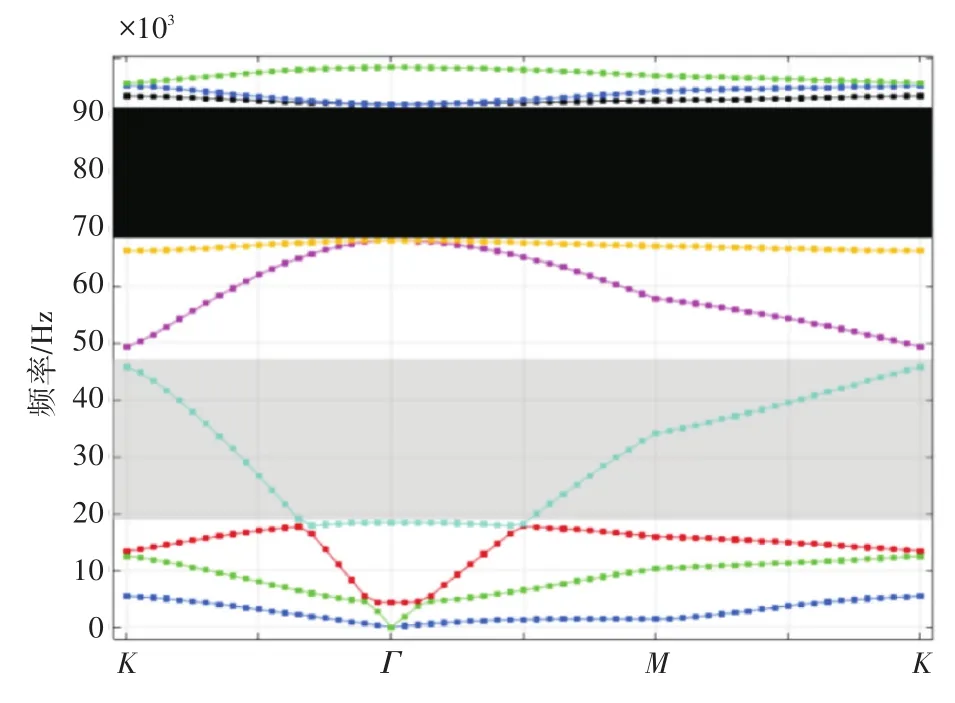
图3 波矢扫掠蜂窝单元的频散曲线及频带示意

此外，能带结构还可以反映出五模材料中不同类型波传播的相速度，以频散曲线中经过原点Γ解耦后的纯横波与纯纵波为例，其在五模材料中传播的相速度可由原点附近频散曲线的斜率计算得到。将之引入弹性动力学方程，即可得到结构的等效模量。对于五模材料，因为拉压与剪切的解耦，传统的弹性张量可退化为3×3的弹性矩阵：

考虑到二维五模材料周期性的特点，可以通过单个声子晶体单胞的能带结构分析其模量，由于单胞不具有实际的宏观弹性模量，故将上述矩阵以等效参数进行描述［15］：

其中，等效模量参数与相应方向相速度的关系为［16］

式中CLx，CLy，CTx即为弹性波波矢在二维五模超材料中激励的x，y方向纵波波速以及横波波速，除主轴方向外，还有正剪应变耦合产生的xy斜向极化波CqL，CqT，在本文的主要模量计算中暂不作考虑。ρeff为五模声子晶体单胞的等效密度，可以通过单胞质量对六边形范围求平均值得到。据此可以计算出二维各向同性五模材料的等效模量，以该均质蜂窝单胞为例，由式（3）可求得等效弹性模量，等效剪切模量0.03GPa。因此，图2（a）中二维均质蜂窝状五模材料的品质因数约为76。

3.2 各向异性构型的数值仿真结果

在均质结构的研究结果之上，讨论上述三种各向异性构造方法对频带宽度及品质因子的影响。各向异性的引入使得布洛赫边界相比于均质结构时发生改变，这是因为单胞的高度对称模式失效，波矢扫掠的不可约布里渊区将从1/12的正六边形区域变为整个单胞空间。三种构型的声子禁带、单模带隙与品质因子随各向异性程度的变化情况如图4～7所示。

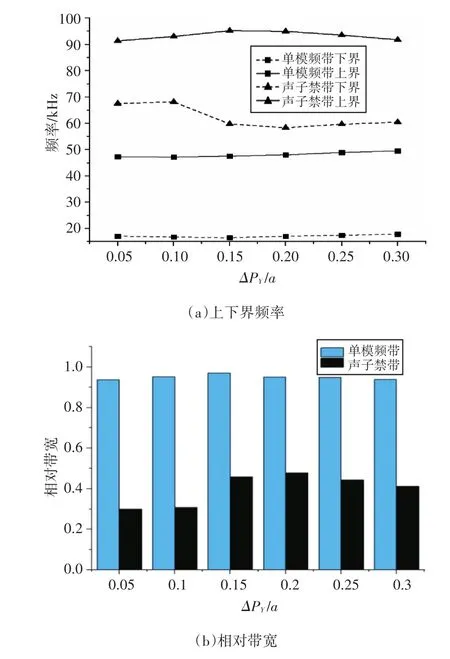
图4 模型α的单模频带与声子禁带

图5 模型β的单模频带与声子禁带

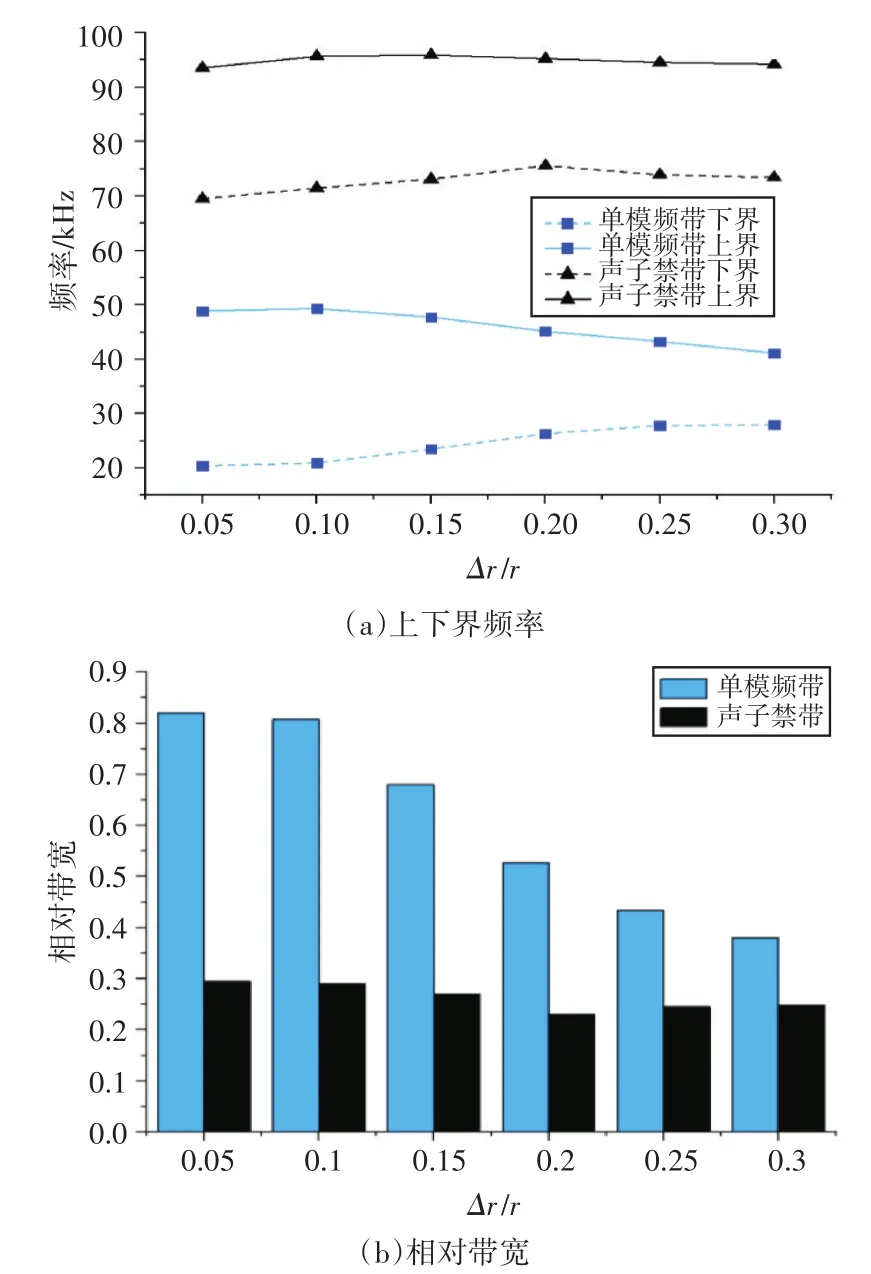
图6 模型γ的单模频带与声子禁带

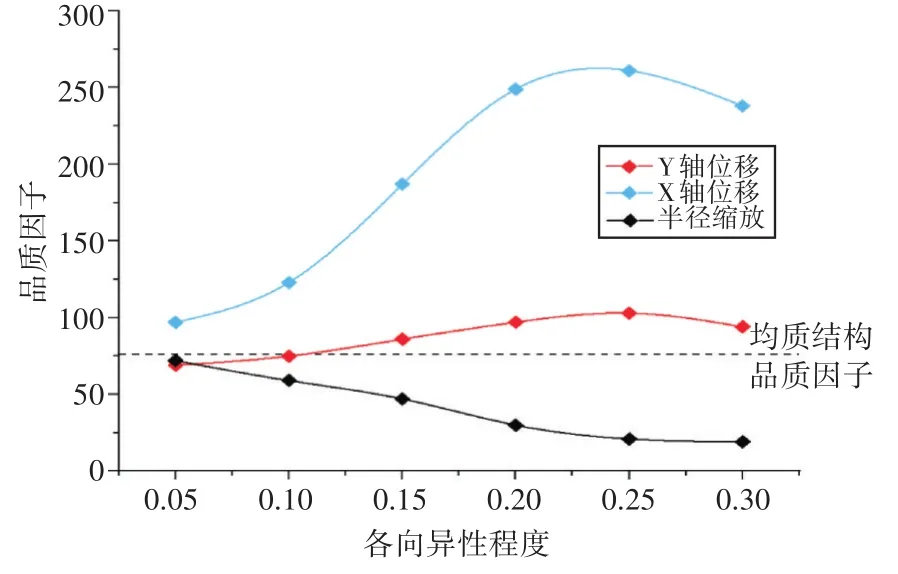
图7 三种各向异性构造方法对蜂窝结构品质因子的影响

在模型α中，随着P点在纵向的位移，单模频带下界逐步降低，在ΔPY/a=0.15时达到最低值16.51kHz，随后缓慢增加至17.91kHz。单模频带上界从47.31kHz增加至49.55kHz，相对带宽在0.92～0.97之间变化，相对于均质结构提升了约8.9%。第一声子禁带下界在ΔPY/a=0.1之后明显降低，最低值达到58.34kHz，上界则在91.33 kHz～95.22kHz之间变化，相对带宽在ΔPY/a=0.2时达到0.47，相对于均质结构提升了56.7%。

在模型β中，随着P点横向位移，单模频带的下界有明显降低的趋势，从19.16kHz降低至15.5kHz，考虑到五模材料的纵向框架结构被改变，抗剪性能被进一步削减，横波频段随着各向异性的增大而逐步压缩。单模频带上界相较均质结构也有较大提升，在ΔPY/a=0.2时达到最高值53.05kHz。相对带宽在0.88～1.08之间变化，相对于均质结构提升了约21.3%。声子禁带相较于均质结构变化不大，下界与上界的最低与最高值分别为68.21kHz和90.12kHz，相对带宽在0.26左右浮动，相对于均质结构降低了约13.3%。

在模型γ中，单模频带的上下界有明显贴近的趋势，在Δr/r=0.3时下界达到了27.97kHz，上界则降低至41.11kHz，单模频带被显著压缩。这可能是随着圆配重半径的增大，对蜂窝薄壁的加固影响显著提升，五模材料的固体属性被增强而近似液流体的属性被削弱导致的。单模区域的相对带宽从0.82降至0.38，相对于均质结构降低了约57.3%，并且随着配重半径的各向异性变化，单模频带还会进一步收窄。声子禁带的上下边界均明显提升，最高值分别达到了75.56kHz与95.92kHz，其相对带宽在0.24～0.31之间变化，相对于均质结构基本持平。

三种各向异性构造方法中，模型α对均质蜂窝构型的品质因子影响较小，在ΔPY/a=0.25时达到接近100，此后逐渐减小；模型γ由于配重半径的增加显著加强了结构的抗剪性能，导致其等效剪切模量随着各向异性的提升而增大，品质因子始终低于均质结构；模型β则有效抑制了剪切波，在ΔPX/a=0.25时，品质因子达到最大值261，相较于二维均质蜂窝五模材料提升了3.43倍。

4 结语

本文针对二维蜂窝五模材料的各向异性进行了调节，通过对基本周期单元内配重的x、y轴平移、配重缩放，设计了三种各向异性构型，并通过有限元仿真计算给出了不同构型中能带结构特性、品质因子与各向异性程度的关系。研究表明，与二维均质蜂窝五模材料相比，各向异性结构的单模频带与声子禁带的相对带宽均得到显著增加。同时，引入各向异性也可以提升二维五模材料的品质因子，声波调控的性能得到改善。但值得一提的是，由于结构剪切模量的减小，其力学性能与宏观稳定性势必受到影响。此外，由于单胞的对称性改变，结构加工难度增加，对制备工艺也提出了更高要求。因此，设计兼顾高品质因子与一定的力学性能，满足不同频率条件下的声波调控，同时具有良好可加工性的蜂窝结构将是二维五模材料后续研究的重点内容。