指定删失比例的生存数据模拟及R实现*
南京医科大学公共卫生学院生物统计学系(211166)
蔡丽馨# 仲子航# 杨 旻 于全骥 周佳薇 倪森淼 于 浩△ 柏建岭△
【提 要】 目的 探讨生成具有指定删失比例的模拟数据的新方法,并编写完整的模拟数据产生的R代码,方便使用。方法 基于Cox比例风险模型框架分别推导考虑和不考虑协变量情况下的删失参数的闭式表达式或核密度估计,并基于R 4.0.2软件编写函数模拟产生满足指定删失比例的生存数据。通过1000次模拟数据来验证生成数据的删失比例是否与指定的删失比例一致。结果 函数CenDatNoCov、CenDatBin、CenDatNorm和CenDatMixed可分别返回不考虑协变量,协变量为二项分布、正态分布以及混合分布情况下的删失数据,其中后三者内嵌的函数CensProbBin,CensProbNorm,CensProbMixed可分别得到相应情况下的删失参数值。模拟生成数据的删失比例与指定的删失比例近似相等。结论 本研究所提供的方法及编写的R函数可有效生成指定删失比例的数据。
生存数据的相关模拟近年来越来越受到医学研究者的关注。一方面,随着临床试验的设计方法越来越复杂,《药物临床试验适应性设计指导原则(征求意见稿)》[1]中明确指出了统计模拟试验的优点及重要性,而在许多临床试验,尤其是肿瘤药物研究中,主要终点指标通常为生存数据,如OS,PFS等[2-5]。另一方面,生存数据统计方法的研究也依赖于模拟试验对相关性能进行评价[6-7]。对于生存数据而言,在实际情况下,受人力、财力、资源等限制,通常会有部分受试者的终点事件在研究结束时仍未被观察到,从而被标记为“删失”。研究表明删失会带来许多问题,同时对不同的分析方法产生一定的影响[6,8],因此,为反映所研究方法的真实性能,能够有效控制删失比例在预设的水平显得十分必要。针对这一需求,我们通过文献检索发现目前国内对此研究较少,有研究者提出在产生的完整数据中随机抽取指定比例的观测作为删失,并对此部分观测从新的删失分布中产生删失时间作为最终的生存数据,这一方法较为理想[9]。更常用的方法是基于特定的分布同时生成事件发生时间和删失时间两个变量,通过逻辑判断来决定最终状态,在此框架下,一些学者通过选取不同参数值进行重复手工调试以确定平均删失比例满足要求的参数值[10],这一方法对计算机性能的要求很高,同时会消耗较长的时间;Fei Wan等人提出一种方法[11],基于Cox比例风险模型在考虑了删失分布、协变量分布及基线风险后可以给出分布参数值的闭式表达,从而使得模拟的生存数据具有指定的删失比例。本文基于此方法,给出不考虑协变量和考虑协变量的不同情形下产生指定删失比例的生存数据的方法,同时编写了完整的R代码以供使用。
方法与原理
为了模拟删失数据,我们常用的一种方法即生成事件发生时间T和删失时间C两个变量,并记δ=I(T≥C)为删失状态变量,即当T 事件发生时间通常可以通过指数分布、Weibull分布、Gamma分布、log-normal分布及log-logistic分布等来描述,其中Weibull分布Weibull(α,λ)相较于Gamma分布、log-normal分布等形式更为简洁,相较于指数分布又可通过额外的尺度参数(scale parameter)λ和灵活的形状参数(shape parameter)α取值来弥补指数分布的局限性,形状参数的不同取值可以描述在研究期间风险的变化趋势而不再是指数分布假设下单纯的风险恒定,因此其应用最为广泛。 删失时间通常认为服从均匀分布uniform(0,θ),指数分布exp(θ)或者Weibull分布Weibull(α,θ),其中θ为所谓的删失参数。 本文基于事件发生时间服从Weibull(α,λ)分布,删失时间服从于均匀分布uniform(0,θ)来模拟生成指定删失比例的生存数据,考虑协变量时采用Cox模型。 1.不考虑协变量的指定删失比例生存数据 (1)事件发生时间T的参数分布 Weibull分布的概率密度函数和风险函数为: (1) h(t;α,λ)=αλ-αtα-1 (2) 其中,λ>0,α>0,t≥0 (2)满足指定删失比例的删失时间C的参数分布 由于所谓删失参数θ的取值可直接影响最终的删失比例p,因此我们在给定一系列参数及相关分布的情况下构建p与θ的关系,对θ值进行反推以满足需求。设定删失时间C服从均匀分布uniform(0,θ),即其密度函数为: (3) 各个体的删失概率为: (4) 2.考虑协变量的指定删失比例生存数据 (1)事件发生时间T的参数分布 基于Cox风险比例模型考虑协变量的影响。对于第i例受试者,其协变量记为d维向量Xi,回归系数向量记为β,基线风险函数记为h0(t),则风险函数可以表示为: (5) 上式中,exp(X′iβ)λ-α=[λexp(-X′β/α)]-α,记λi=λ[exp(-X′iβ/α)]=exp[-(-αlogλ+X′iβ)/α],则考虑协变量影响所对应的事件发生时间将服从Weibull(α,λi),密度函数为: (6) (7) 由此可构建Xi与λi间的关系,将复杂的多维问题简化为对单变量的处理。不难发现,当Xi中的变量类型相同时,fλ(u)可以准确给出。 (8) (9) 当Xi为多类型变量的组合时,我们无法准确地给出该密度函数表达式,此时可以通过非参数核平滑方法得到λi的密度估计函数,如选用高斯核函数来估计。 (2)满足指定删失比例的删失时间C的参数分布 对于删失参数的求解步骤同上,但需考虑不同个体的删失概率推导总体的删失率。仍假设删失时间C服从均匀分布uniform(0,θ),即其密度函数为:g(c|θ)=1/θ,0 ①描述各个体的删失概率: p(δ=1|Xi,θ)=p(C≤T<∞,0≤C<θ) (10) ②基于个体水平的删失概率估计总体的平均删失率: (11) 其中,fx(·)为d个独立协变量X的联合密度函数,D为X的概率空间。前面已介绍可通过估计以λi的概率密度fλi(u)来简化计算。 ③通过对等式γ(θ)=p(δ=1|θ)-p=0进行求解得到θ值,其中: (12) 若p(δ=1|λi,θ)有闭式表达式,则式(11)在简单的积分同样可得到明确的表达式进而求得解析解,但若无法直接写出该条件删失概率的表达式,则需对式(11)进行二重积分后求解。 在事件发生时间满足Weibull分布的情况下,记其基线风险函数h0(t)=αλ-αtα-1,相互独立的协变量为X,则事件发生时间可认为来自Weibull(α,λi),删失时间服从uniform(0,θ),则可求得各个体删失的概率为: p(δ=1|Xi,θ)=p(δ=1|λi,θ)=p(C≤T<∞,0≤C<θ) (13) z=(c/λi)α 其中γ(1/α,(θ/λi)α)为下不完全Gamma函数。 给定回归系数β=<β1,β2,β3>,记β0=-αlogλ: ①若X均为连续性变量,如4个均来自N(0,1),则: (14) ②若X均为二分类变量,如分别来自B(p1),B(p2),B(p3),B(p4),则 (15) ③若X为不同类型的变量,如分别来自4个不同分布,包括N(0,1),B(p2),Poisson(n3),Uniform(0,1),则需要通过核平滑估计来估计λi的概率密度fλi(u)并带入计算。 1.不考虑协变量 我们构建CenDatNoCov()函数来产生指定删失比例的生存数据,输入参数包括Weibull(α,λ)的形状alpha和尺度参数lambda,指定的删失比例cens.p及样本量size。由于不考虑协变量,我们仅需通过uniroot()函数对式(6)进行求根即可得到删失参数theta,其中下不完全Gamma函数γ(a,x)在R中可定义为pgamma(x,a)*gamma(a)。 CenDatNoCov<- function(alpha,lambda,cens.p,size){ theta <- round(uniroot(function(x)lambda/(alpha*x)*pgamma((x/lambda)^alpha,1/alpha)*gamma(1/alpha)-cens.p,c(0.00001,1000))$root,3) #据方法与原理的描述产生删失的生存数据 data<-data.frame( T=rweibull(size,alpha,lambda), C=runif(size,0,theta)) cens.data<- data.frame(time=ifelse(data$T<=data$C,data$T,data$C), status=ifelse(data$T<=data$C,1,0)) return(list(theta=theta,cens.data=cens.data)) } 例1 假设事件发生时间T来自Weibull(2,4),删失时间C服从uniform(0,θ),指定的删失比例为30%,样本量为200,即CenDatNoCov(alpha=2,lambda=4,cens.p=0.3,size=200)。求得θ=11.816即为了使得最终的删失比例达到30%,需设定删失参数θ为11.816。为了检验该参数是否可以满足需求,我们可以生成1000组T和C并进行删失状态的判断计算其平均删失率,设定随机种子数为20200810,结果为0.30107,符合我们的预设的删失比例。 2.考虑协变量 (1)二分类协变量 我们构建CenDatBin()来产生均为二分类协变量的删失数据,输入参数包括Weibull(α,λ)的形状alpha和尺度参数lambda,指定的删失比例cens.p,事件发生时间的风险模型回归系数beta,各协变量的分布参数p,样本量size及随机种子数seed;返回列表包括删失参数theta及所生成的生存数据。其中内置的CensProbBin()函数可返回对应的删失参数theta值。 CenDatBin<- function(alpha,lambda,cens.p,beta,p,size,seed=20200812){ alpha=alpha # weibull分布中的形状参数 lambda=lambda # weibull分布中的形状参数 cens.p=cens.p#预设的删失比例 beta=beta# Cox模型中各协变量的系数 p=p# 各二分类协变量的发生率 n=size#产生数据的样本量 #构建删失率函数,参数为均匀分布中的删失参数θ,返回值为给定θ后估计的总体删失率: CensProbBin <- function(theta){ beta.0 <--alpha*log(lambda) #计算新常数以代入公式(7) #得到协变量取值的所有组合 LenCovar <- length(beta) #获得协变量个数 CombInd <-list(NULL) ncomb <- c() finalInd <- c() #所有组合中,取值为1的协变量下标矩阵 for(i in 1:LenCovar){ #通过循环得到至少1个协变量取值为1的所有组合下标 ind <- combn(1:LenCovar,i) #其中i个协变量取值为1的变量下标组合 CombInd[[i]]<- ind for(j in 1:ncomb[i]) { location <- c(CombInd[[i]][,j],rep(0,(LenCovar-i))) #以0补齐取值为0的协变量下标 finalInd <- cbind(finalInd,location) #得到组合的下标矩阵共LenCovar行,2^LenCovar列 } } # 根据各协变量的下标组合进行赋值,得到最终的取值组合 comb <- matrix(0,nrow = LenCovar,ncol = 2^LenCovar) #构建协变量取值为0的矩阵 for(i in 1:2^LenCovar-1){ comb[finalInd[,i],i]=1 #将下标矩阵中不为0的协变量取值赋为1 } # 据公式(9)构建单变量,简化计算 lambda.i<-exp(-(beta.0+apply(beta*comb,2,sum))/alpha) #计算在对应协变量下的个体条件删失概率 cond.cens.Prob<-(lambda.i/(alpha*theta))*pgamma((theta/lambda.i)^alpha,1/alpha) * gamma(1/alpha) #计算该变量的分布律 pdf.lambda.i<-apply(matrix(p,nrow=LenCovar,ncol = 2^LenCovar)**comb*((1-matrix(p,nrow=LenCovar,ncol = 2^LenCovar))**(1-comb)),2,prod) return(t(cond.cens.Prob)%*%pdf.lambda.i) } #求解删失参数值 theta<- round(uniroot(function(x)censProbBin(x)-cens.p,c(0.0000001,100))$root,3) #生成模拟协变量值 set.seed(seed) a<-c() cov<-sapply(p,function(x)cbind(a,rbinom(n,1,x))) colnames(cov)<- paste(“x”,1:length(p),sep=“”) #指定rweibull()函数中scale参数值为lambda*exp(-1/alpha*(Xβ)) EVENT<-rweibull(n,alpha,lambda*exp(-1/alpha*(cov%*%beta))) data<-as.data.frame(cbind(id=1:n,cov=cov,EVENT=EVENT,C=runif(n,0,theta))) #据方法与原理的描述产生删失的生存数据 data$time=ifelse(data$EVENT<=data$C,data$EVENT,data$C) data$status=ifelse(data$EVENT<=data$C,1,0) return(list(theta=theta,cens.data=data)) } 例2 以四个协变量分别来自B(0.3),B(0.4),B(0.5),B(0.6)为例。CenDatBin(alpha=2,lambda=4,cens.p=0.3,beta=c(-0.1,0.2,-0.3,0.4),p=c(0.3,0.4,0.5,0.6),size=200,seed=20200812),得到θ=11.116,即为了达到30%的删失比例,删失时间的分布uniform(0,θ)的参数应设为11.116。可通过上述方法生成1000次模拟数据来验证结果,当种子数设定为20200810时,得到的删失比例平均值为0.30132,满足预设的要求。 (2)正态分布协变量 我们构建CenDatNorm()来产生均为正态分布协变量的删失数据,输入参数基本同上。内嵌计算删失参数的相关函数为CensProbNorm(),通过求根即可获得theta值: CensProbNorm<-function(theta){ beta.0 <- -alpha*log(lambda) # alpha、lambda分别为weibull分布中的形状、尺度参数 # 据公式(8)得到单变量λi的概率密度函数,简化计算 PdfLambdai<-function(u)dlnorm(u,-beta.0/alpha,beta%*%beta/alpha^2) # 据公式(13)得到条件删失概率 CondCensProb<-function(u)(u/(alpha*theta))*pgamma((theta/u)^alpha,1/alpha)* gamma(1/alpha) # 据公式(14)得到删失概率的表达式 cens.Prob<-integrate(function(u){PdfLambdai(u)*CondCensProb(u)},-Inf,Inf)$value return(cens.Prob) } 例3 以四个来自N(0,1)的协变量为例,给定alpha=2,lambda=4,预定的删失比例cens.p=0.3,求解对应的删失参数,theta<-round(uniroot(function(x)CensProbNorm(x)-cens.p,c(0.0001,1000))$root,3),得θ=11.849,即为了达到30%的删失率,删失时间的分布uniform(0,θ)的参数应设为11.849,同理,模拟1000次得到的平均删失率为0.30831。 (3)混和协变量 我们构建CenDatMixed()来产生混合分布协变量的删失数据,输入参数除同上的基本参数外,还包括描述所有混合变量类型的参数calss,各分布的对应参数para。由于协变量类型不统一,我们很难推导出λi的概率密度fλi(u),因此我们采用高斯核密度估计方法,删失参数的估计可通过内嵌的CensProbMixed()函数获得: CensProbMixed<- function(class,para,theta){ set.seed(20200810) #高斯核密度估计lambda.i的密度函数 n<-10000 # 以10000个点来估计lambda.i的密度分布 # 生成构成lambda.i的相关变量值以提供拟合联合分布的数据 nNorm<- length(class[which(class==“N”)]) nBin<- length(class[which(class==“B”)]) nPos<- length(class[which(class==“P”)]) nUni<- length(class[which(class==“U”)]) if(nNorm> 0){ a<-as.matrix(mapply(rnorm,n,0,rep(1,nNorm))) } if(nBin> 0){ b<-as.matrix(mapply(rbinom,n,1,para$B)) } if(nPos> 0){ c<-as.matrix(mapply(rpois,n,para$P)) } if(nUni> 0){ d<-as.matrix(mapply(runif,n,para$U[,1],para$U[,2])) } x <-cbind(a,b,c,d) # 构建lambda.i beta.0<--alpha*log(lambda) lambda.i<-exp(-(beta.0+x%*%beta)/alpha) max.lambda.i<-max(lambda.i) min.lambda.i<-min(lambda.i) PdfLambdai<-function(u){ # 得到并返回lambda.i的gauss核密度估计 dens<-density(lambda.i,bw=“nrd0”,kernel=“gaussian”,na.rm=TRUE) y.loess<-loess(dens$y~dens$x,span=0.1) pred.y<-predict(y.loess,newdata=u) return(pred.y) } # 据公式(13)得到条件删失概率CondCensProb<-function(u)(u/(alpha*theta))*pgamma((theta/u)^alpha,1/alpha)*gamma(1/alpha) # 得到删失概率的表达式 cens.Prob<-integrate(function(u){PdfLambdai(u)*CondCensProb(u)},min.lambda.i,max.lambda.i)$value return(cens.Prob) } 例4 以四个协变量分别来自N(0,1),B(0.5),Poisson(5),Uniform(0,1)为例,给定alpha=2,lambda=4,指定的删失比例cens.p=0.3,theta.mixed<- round(uniroot(function(y)CensProbMixed(class=c(“N”,“B”,“P”,“U”),para=list(B=c(0.5),P=c(5),U=matrix(c(0,1),ncol=2,byrow=TRUE)),y)-cens.p,c(0.001,100))$root,3),得θ=22.698,即为了达到30%的删失率,删失时间的分布uniform(0,θ)的参数应设为22.698,同理,模拟1000次得到的平均删失率为0.29706。 为了通过模拟试验对统计分析方法的表现性能进行评价[6,13],指定删失比例的生存数据在研究中通常被广泛应用。 肖媛媛等人提出的方法基于完全随机删失的假设,其使得整体的删失状态服从二项分布,而每个个体的删失时间则服从不同的均匀分布。该方法中删失时间的分布依赖于事件发生时间,从而使得其产生的模拟数据变异性更大,本研究的方法相比之下显得更为稳定。 钱俊等人提出的大量取值通过模拟调试确定最终参数的方法虽然简单,但如取值范围选择不当将消耗大量的计算机资源和时间[10]。基于Fei Wan提出的框架[11],本文介绍的方法可通过闭式表达式或者核密度估计方法得到删失时间的分布参数从而生成满足需求的生存数据,极大地提高了计算效率。同时,我们基于最基本的组合情形编写了完整可用的生成删失数据的函数:在事件发生时间和删失时间分别为Weibull分布和均匀分布的条件下,当无需考虑协变量时,可通过CenDatNocov()快速生成相关数据;当考虑协变量对时间的影响时,针对单纯二分类变量的CenDatBin(),针对正态分布数据的CenDatNorm()以及针对混合型协变量CenDatMixed()均可返回删失参数及具有指定删失比例的包含协变量的生存数据。相关的参考代码可通过https://github.com/zihang1012/simulated-survival-data-with-predefiend-censoring-rate-.git获得。但是,由于本方法是在寻找表达式的解,因此会消耗一定的时间,此外,如果参数设置较为极端,可能会超过预先设定的寻根范围,需要使用者额外调整函数中预先设定的界值。 结合各自需求,读者可基于本研究进一步拓展,如可通过指定基线中位生存时间,反推事件发生时间的分布参数得到满足中位生存时间要求的基线生存数据;也可通过引入分组变量并指定回归系数取值以模拟具有不同疗效的RCT数据等。 本研究建立了一套科学可操作的模拟方法,给出了生存数据模拟研究中关于指定删失比例的解决方案,具有实际应用价值。本研究的局限性在于指定删失时间分布为均匀分布,其他分布类型的删失时间值得进一步研究。



R实现与应用
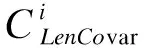
讨 论

