基于深度学习的大规模肿瘤数据生存分析*
中国人民大学应用统计科学研究中心,统计学院(100872) 李 嵘 张文丽 李 扬 林存洁
【提 要】 目的 将深度学习方法应用在大规模肿瘤数据中,并预测肿瘤患者的个体生存情况,提升预测精度,为个体化治疗方案提供参考。方法 以老年乳腺癌数据为例,将生存时间划分成离散区间,通过神经网络方法预测患者在各离散区间内的死亡概率,实现个体生存函数的预测。结果 对于19576例老年女性乳腺癌的个体生存函数预测情况,本文提出的方法预测效果好于其他的模型,表现在有更大的c-index指标和更大的log-rank统计量值。结论 基于深度学习的生存函数预测有较大的灵活性,不受Cox模型比例风险假设的限制,能够处理大规模数据,并且对个体生存函数的预测更加准确。
全球癌症负担日益加重,肿瘤的发病率和死亡率日益增加,已成为威胁人类健康的主要危险因素。随着电子病历(EMR)和肿瘤基因组学的发展与普及,肿瘤病人的相关临床数据量不断增加,而大规模的肿瘤数据为精准医学提供了良好的研究基础[1]。精准医学自提出以来一直被广泛重视,2015年3月,我国科技部首次召开国家精准医学战略专家会议,计划启动中国的精准医学计划,随后精准医学被列入国家重点研发项目并正式进入启动阶段[2-3]。精准医学根据患者的特异性进行个性化的预防或治疗干预,通过预测肿瘤患者的个体生存情况来确定个体化治疗方案。本文的研究对象为老年乳腺癌患者,乳腺癌是女性最常见的恶性肿瘤之一,随着人口老龄化及女性平均寿命的延长,老年乳腺癌(以大于65岁为界限)发病率明显增多。由于老年病人的体质和健康状况差异较大,尚无规范的治疗模式,因此对于老年乳腺癌的治疗应该按照个体化原则确定治疗方案[4]。
预测生存函数是生存分析中的重要任务,而大规模肿瘤数据为研究建立了基础的同时也带来了挑战。庞大的数据量使得经典的Cox模型难以计算,另外,Cox模型假设风险函数的对数是解释变量的线性组合且解释变量的影响不随时间变化,该比例风险假设在实际问题中难以被满足。近年来,随着机器学习的发展,利用深度学习方法处理生存数据的研究也取得了一些进展,突出的方法包括Cox-nnet[5]、DeepSurv[6]和Nnet-Survival[7]。其中Cox-nnet方法利用一层神经网络进行降维后将输出的结果作为解释变量拟合Cox模型,DeepSurv方法则是基于Cox模型的部分似然函数利用深度学习模型拟合风险函数。但是Cox-nnet和DeepSurv这两种方法仍在不同程度上保留了Cox模型的假设,因此具有一定的局限性。而Nnet-survival方法则是将生存时间离散化,然后估计各区间的条件风险函数。在本文中,我们借鉴Nnet-Survival的思想,但是更加关注每个离散区间上生存函数的估计,把生存分析问题转化成深度学习问题,进而提高生存函数的预测精度。该方法完全摒弃了Cox模型的假设,能够更加灵活地处理生存数据,给出更加准确的预测结果,同时保持了深度学习算法对大规模数据的有效性,因此能够更好地适用于大规模肿瘤数据的生存分析。
原理与方法
假设我们的观测数据是右删失数据,即存在部分样本,截止到观测时间结束,感兴趣的事件(例如死亡事件)仍没有发生。不妨设观测样本为:(Ti,Zi,δi),i=1,…,n。其中Ti=min(Xi,Ci),Xi表示个体i的真实生存时间,Ci表示个体i的删失时间,Ti即为可观察到的两者中的最小值,Zi表示p维协变量。δi是指示变量,δi=0表示数据删失(即Ci pj=P(tj-1 其中S(t)=P(T>t)表示生存函数。如图1所示,在第j个区间终点tj处的生存函数为: 通过估计离散区间端点处生存函数的值就可以很好地近似完整的生存函数曲线,因此对于某个个体而言,其生存函数可以对应到一组长度为M的向量p=(p1,p2,…,pM),这里p表示M个离散区间中死亡事件发生的概率。从而对于生存函数的估计就转化成对于p的估计。考虑到解释变量对p的影响可能是复杂的非线性关系,也可能随着时间进展而变化,因此,采用深度学习对p进行估计。 图1 离散区间结构 1.神经网络的结构 神经网络的结构包括输入层、隐藏层和输出层。本文采用全连接神经网络,即层与层之间每个神经元都有连接。 (1)输入层 输入层是影响生存时间的解释变量Z,输入层神经元个数等于解释变量的维数。 (2)隐藏层 隐藏层的层数和各层神经元的个数可以自行选择。隐藏层采用sigmoid激活函数。隐藏层中每一个神经元的输出值是所有连接到该神经元的输入值的线性组合再经过sigmoid激活函数非线性处理后的结果。 (3)输出层 一般地,离散区间的个数M可取15~40个且模型的表现对离散区间的选择比较稳定,本文通过下式确定前疏后密的区间端点[7]: 其中,t*=0.27tmax,tmax为区间终点。 2.神经网络的训练 (1)构建目标函数 其中,第二项为正则项,wk记为神经网络中的参数,λ为调节系数控制惩罚力度的大小,通过对参数添加L2惩罚以防止模型过拟合。 (2)Minibatch梯度下降算法 求解神经网络以使得目标函数最小化,通过反向传播算法对目标函数进行求导,然后采用Minibatch梯度下降算法对网络中参数进行更新。Minibatch梯度下降法适用于大规模数据集,由于个体似然函数间互相独立,因此可以将大规模数据集拆分成多个小样本集,在每个小样本集中更新参数[8-9]。首先将全部样本划分为训练集和测试集,记训练集中的样本可以划分为B个小样本集,每个小样本集中包含的样本点个数为nb(b=1,…,B)。在每个小样本集中通过以下的方式依次更新参数: 其中η(b)表示第b次迭代中的步长,也称作学习率,w(b)-w(b-1)表示动量,记录了上一次迭代时系数改变的方向,增加动量项可以在一定程度上避免陷入局部最优点及大幅度震荡。B次更新记作一代训练,一代是指遍历了训练集一次,本文中一代训练内采用相同的步长,设置步长的初始值为0.005。再将上述一代训练重复至收敛,本文为防止过拟合,设置停止准则为连续300代更新之后测试集上的目标函数没有减少则停止训练。为提高收敛效率,设置步长为每100代训练以0.8倍减小。 (3)超参数选择 上述Minibatch梯度下降算法中包含一系列超参数,包括目标函数中正则项的调节系数λ,神经网络的隐藏层数,各隐藏层神经元个数及更新准则中的动量项参数α。本文通过比较各组超参数组合下测试集的目标函数值以确定使得测试集目标函数值最小的超参数组合。 本文通过深度学习预测老年乳腺癌患者的生存函数,数据来源于美国国立癌症研究所SEER(Surveillance,Epidemiology,and End Results Program)数据库,分析1994-2003年年龄大于等于65岁的19576例女性乳腺癌患者的病历资料。通过预测其生存函数来了解患者的生存情况以便更好地做出治疗决策。 1.数据描述 该数据中记录病例的生存时间的中位数是119个月,观测到的最长生存时间为263个月,删失率为5.9%。连续变量中只有肿块大小存在缺失,缺失比例为11.92%,采用中位数插补。为分类变量添加虚拟变量,其中关于肿瘤位置只设置一个虚拟变量以防止共线性。参考已有文献中对乳腺癌危险因素的讨论[10-11],最终从26个解释变量中选择出8个变量纳入分析,各变量的描述如表1。 表1 解释变量统计表 绘制KM曲线拟合整体的生存函数如图2,总体生存函数在150个月之前下降速度略慢于150个月之后,表示后期风险略大于前期。 图2 老年乳腺癌患者KM生存曲线 2.预测结果比较 本文基于深度学习预测老年乳腺癌患者的个体生存函数,划分36个离散生存区间,通过估计各区间内的死亡概率得到各区间终点处的生存函数的估计,将该方法记为DL-Survival。现有的生存函数估计方法包括Cox模型,以及利用深度学习处理生存数据的Cox-nnet、DeepSurv和Nnet-Survival。分别采用这五种方法预测老年乳腺癌的生存函数,并通过c-index和log-rank两个指标评价各种方法的预测准确性,这两个指标均是生存分析中常用的评价指标[12-13]。c-index计算所有可比的个体对中估计结果的相对关系和实际相对关系一致的比例,是衡量生存分析模型表现的常用指标,其大小在0到1之间,越接近1表示方法的预测精度越高。log-rank检验统计量的原理是先根据预测结果把人群按照中位数分为高风险人群和低风险人群,然后对这两组人群的KM估计曲线进行log-rank检验。log-rank检验统计量值越大表示方法区分高风险和低风险人群的效果越好。各方法的比较结果如表2所示,本文提出的DL-Survival方法在个体生存函数的预测中表现最好。 表2 各方法对老年乳腺癌患者生存函数预测结果比较 对于个体生存函数的预测有助于掌握患者的生存情况,以便优化信息和决策。本文采用深度学习的方法,通过估计离散区间的死亡概率预测个体的生存函数。不同于KM方法对群体生存情况的估计,本文基于个体特征对每个患者的生存函数进行预测。同时本文提出的深度学习算法摒弃了Cox模型中比例风险假设,在实际应用中会更加灵活。在满足等比例风险的条件下与基于Cox的方法能达到相同的效果;在不满足等比例风险的条件下能够优于基于Cox的方法。而相比于其他不受比例风险限制的机器学习方法,本文提出的方法更加直观地预测生存函数,并且可以处理较大规模的数据,其适用性更加广泛。然而在实际应用中运用哪种方法需要综合考虑,例如,当样本量较小时,深度学习方法由于训练样本量不足易产生过拟合,预测结果不一定优于Cox模型。 对大规模肿瘤数据仍然需要更多探索,大规模数据的特点通常包括样本量大,变量维数多以及数据来源多样化。对于更大样本量的数据,基于个体似然函数相互独立,可以考虑分治法(divide and conquer)以降低计算成本。另外,本文中对于SEER老年乳腺癌患者的分析涉及到的解释变量个数不多,当数据中变量维数较多时,可以考虑在神经网络中加入稀疏层,在预测生存函数的同时进行变量选择[14],以寻找影响老年乳腺癌患者生存情况的风险因素。为充分利用不同实验室或研究机构的数据来源,还可以考虑整合分析方法,探索数据集间的关联性和差异性,有助于精准医学对于不同亚群患者的治疗和决策。

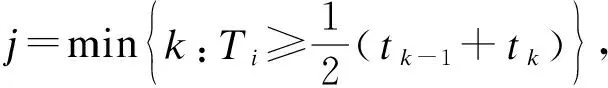
实例分析



讨 论

