无刷直流电机的分数阶建模方法*

吴雨林 李 众

（江苏科技大学 镇江 212003）

1 引言

无刷直流电机的出现代替了许多传统的电机，它是现代电力电子技术、控制理论和电机技术相结合的产物，具有优越的调速性能，主要表现在控制性能好、调速范围宽、启动转矩大、运行平稳、效率高等方面。目前已经被广泛用于诸多高精产业，如国防、航空航天、机器人、工业过程控制、精密机床、汽车电子、家用电器、智能汽车、办公自动化等领域［1］。

分数阶微积分中是近年来常用的一种数学方法，分数阶系统是用分数阶微分方程描述的系统［2］，其中的阶数能够连续变化，可以更准确地描述复杂系统。目前分数阶微积分已被广泛使用于各种领域的建模研究，如电池模型［3］、图像处理［4］流体力学［5］、生物系统［6］等。在电机控制领域，电感和电容这些储能元件本质上是分数阶的，采用分数阶微积分方法能够实现对整个电动机系统建立模型。Rajagopal 等［7］从无刷直流电动机的整数阶模型出发，推导了无刷直流电动机的分数阶模型，对无刷直流电动机的动态特性和混沌控制和稳定进行了研究。余伟等［8］进行了永磁同步电机的分数阶建模研究，该方法将电动机作为一个整体进行建模，未能很好地利用电动机的组成机理。郑伟佳等［9］根据永磁同步电动机的组成机理分别对电磁环节和机械环节进行参数辨识，得到了更好的模拟效果，但是模型实用性较差，需要专门设计多个实验对不同的模型参数进行辨识。本文将采用一种新的方法对无刷直流电机的系统特性进行分数阶建模，以取得对电机更好的模拟效果。

2 无刷直流电机的分数阶建模

2.1 无刷直流电机数学模型

无刷直流电机的数学模型可参考文献［10］，这里给出本文所修改的分数阶模型相关方程。无刷直流电机的电压平衡方程式可表示为

其中分数阶的阶次满足0＜ε＜2。

本文所用的无刷直流电机型号为57BL52-230，其参数如表1所示。控制板使用的是基于意法半导体公司、型号为STM32F302R8 的ARM芯片。

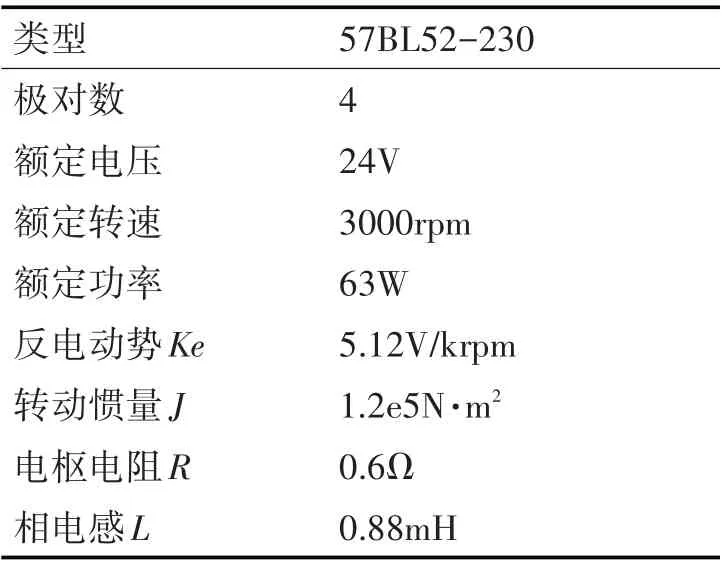
表1 物理样机电机参数

2.2 控制策略

本文无刷直流电机采用的控制策略为基于矢量控制的双闭环PI 控制。外环为速度控制，由速度期望值nref与其实际值n作差，速度控制器选用PI控制。内环为电流控制，定子电流经矢量变换被分解成直轴电流Id（励磁电流）和交轴电流Iq（转矩电流），电动机矢量控制就是控制转矩电流和励磁电流大小。由速度控制器得到Q 轴的期望电流Iqref，本文采取期望励磁电流Idref=0 的控制策略，由期望矢量电流Iqref、Idref与实际值Id、Iq 作差，电流控制器选用PI 控制，得到直轴交轴的电压值，再经矢量反变换，通过SVPWM（空间矢量脉宽调制）得到三相逆变器PWM波的占空比，最终控制电机。

整个控制流程如图1所示。

图1 控制流程框图

3 分数阶模型的参数辨识

3.1 分数阶微积分算子的整数阶近似

分数阶积分器1/sη可用一个一阶积分器和一个用Oustaloup 递推滤波器近似的分数阶微分器串联来逼近［12～14］，设需要逼近的频段范围为（ωL，ωH），Oustaloup 递推滤波器的个数为2N + 1（N 为正整数），则分数阶积分环节可近似成如式（5）所示形式。

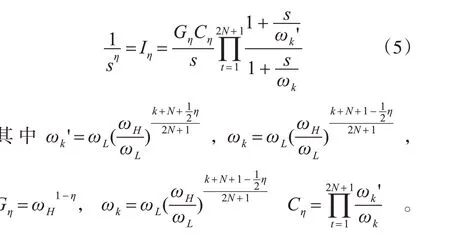
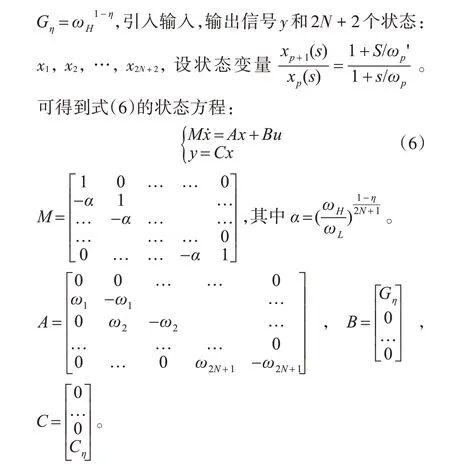
3.2 分数阶阶次的获取

分数阶参数辨识采用基于输出误差的非线性辨识方法［15］，对系统的分数阶模型阶次辨识的方法如下。

在实验平台和仿真模型上加上相同的激励得到响应的实验数据y仿真数据ŷ，详细表现系统的误差的公式为

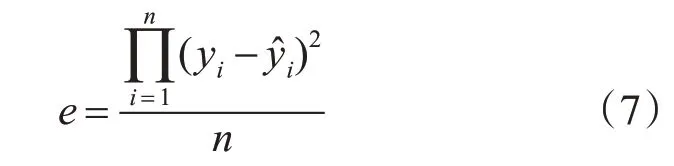
其中n 为采样数据点个数，为了让分数阶模型能更准确地描述电机行为，需要得到系统误差值为最小值时θ和ε的值，将此值作为分数阶模型的阶次参数此时对模型参数选取的问题转变成求解数学模型取得误差函数极小值时对应的参数问题。由于基于机理建立的仿真模型较为复杂不适用复杂的曲线拟合算法，并且参数变化范围不大，同时为了避免陷入局部最优解，本文采用穷举法划区计算，最终得到分数阶模型的参数。具体步骤如下。

1）搭建实验平台，根据已经测得的电机参数利用仿真软件Matlab 建立相应的基于机理的无刷直流电机的整数阶仿真模型和控制器模型，根据前文所述方式建立相应的分数阶仿真模型。

2）在实验平台用阶跃信号测试物理样机，通过数据采集器得到电机的速度响应曲线，将实验数据输入Matlab，用高斯滤波对实验数据进行降噪处理，由于是离散化地采样，在Matlab 默认为是线性插值。滤波处理前后的图形如图2所示。

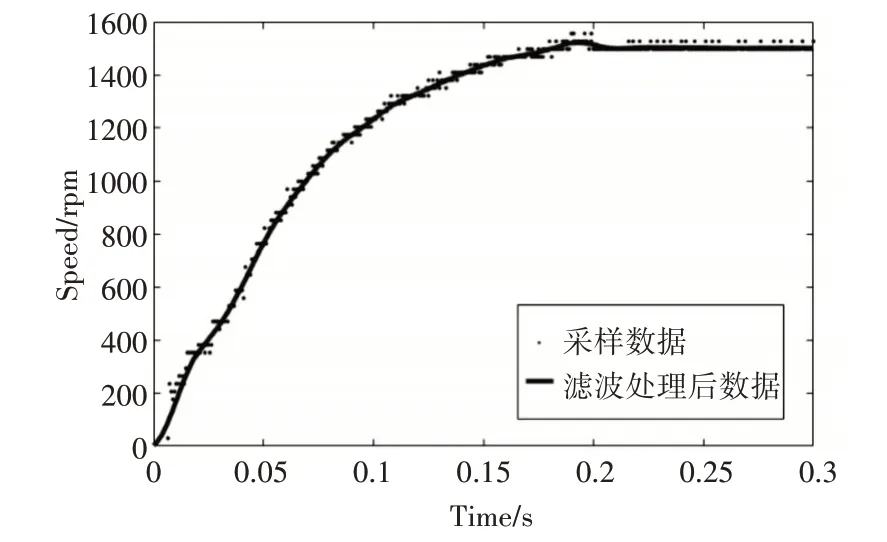
图2 电机采样数据处理

3）保持仿真模型的PI 控制器参数和实验平台的控制器参数一致，用同样的信号测试无刷直流电机分数阶仿真模型，调整θ、ε值，得到分数阶无刷直流电机仿真模型的仿真结果。

4）用经滤波处理后得到的实验数据和分数阶无刷直流电机仿真得到的仿真数据计算系统误差值，其结果如表2，未在表中显示的θ、ε其计算系统误差的结果均大于352。

表2 系统误差值

由表2 可知，θ=0.76，ε=1.10 时，作为测量标准系统误差e 的值最小，这时无刷直流电机分数阶仿真模型阶跃响应的转速曲线对实际电机阶跃响应的转速曲线拟合得最好，因此本文模型选取θ=0.76、ε=1.10 作为无刷直流电机的分数阶模型阶次。分数阶模型对实际电机转速曲线的拟合效果如图3。

图3 转速曲线拟合效果

4 无刷直流电机分数阶模型验证

为了判断无刷直流电机的分数阶模型是否比原来的整数阶模型更准确地模拟了实际电机的行为，需要进一步实验验证。

设计实验分别在不同的速度控制器参数下和不同的输入激励下，比较整数阶模型的系统和分数阶模型与实际电机的差距，结果如下。

1）更改速度控制器参数对仿真模型进行验证，实际电机阶跃响应的转速曲线及整数阶模型和分数阶模型阶跃响应的转速曲线如图4，其中整数阶模型和分数阶模型的系统误差值e 的计算结果分别为532、8311。

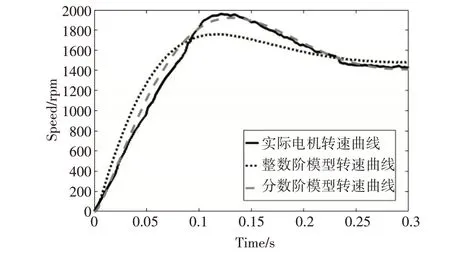
图4 更改控制器参数后模型的模拟效果

2）更改输入激励对仿真模型进行验证，得到的实际电机阶跃响应的转速曲线及整数阶模型和分数阶模型阶跃响应的转速曲线如图5。统误差值e的计算结果分别为938、7495。

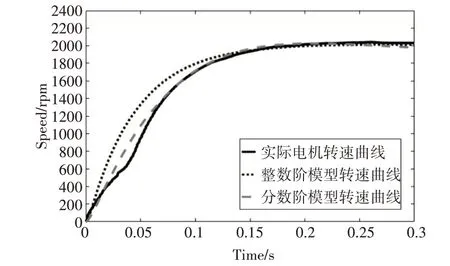
图5 更改输入激励后模型的模拟效果

图4、图5 均可以明显看出分数阶模型比整数阶模型对实际电机有更好的模拟效果。

5 结语

实际系统的复杂性，导致基于已知参数的机理建模的无刷直流电机模型对实际电机的模拟效果很差，而基于数理建模的无刷直流电机的模型则难以对电机仿真模型进行修改。本文提出的无刷直流电机的分数阶建模方法兼具机理与数理建模的优点，且更具有实用性和可操作性。由辨识得到分数阶模型的分数阶阶次，在不同的实验条件下进行实验并对分数阶模型和整数阶模型的仿真结果进行对比表明，分数阶模型比整数阶模型能更精确地模拟实际无刷直流电机的行为。