改进类电磁机制算法预测应用*
杨 云 杨继海
(长安大学信息工程学院 西安 710064)
1 引言
水质预测是水污染防治的有效手段,但是水质因子与水质间是复杂的不确定的非线性关系,实际应用中存在预测结果与实际值偏差较大的难题。
目前主要水质预测方法有时间序列法、回归分析法和神经网络法。时间序列法基于数理统计理论,分析水质指标中的某个检测值的时间序列数据,通过加权平均等数学方法推测未来水质变化趋势。该类方法优点是数学基础完善,但是算法复杂而且预测准确性不高。回归分析法研究部分或全部影响水质变化的因素,建立一元或多元回归模型,常采用最小二乘法估计参数建立回归方程,再用实际变量验证回归方程。该类方法应用较为广泛,在样本量足够大的情况下,可以得到较为准确的预测结果。神经网络法抽象人的推理模式,不需要预先描述输入和输出的数学映射,在未知系统内部复杂机制的情况下,通过对输入样本的训练学习,获得可靠输出[1~4]。与传统水质预测方法比较,神经网络法更适合处理复杂多变和非线性的水环境系统。但是神经网络存在易陷入局部极值和收敛速度慢的不足,所以可以采用遗传算法等全局优化算法改进BP 网络性能,可有效提高收敛速度和预测精度[5~6],以及最新的深度模型[7~10]。本文引入一种新的全局优化算法,类电磁机制算法[11~13],根据传感器边缘计算资源有限不适合深度网络和复杂优化算法的特点,改进类电磁机制算法,优化神经网络模型,有效降低水质因子与水质之间关系模型复杂度的同时提升了预测的精度,研究结果可指导该流域水污染防治和水资源保护。
2 模型与方法
2.1 神经网络
神经网络模型采用误差逆向传播的多层前馈式神经网络,拓扑结构三层:输入层、隐含层和输出层。典型网络模型如图1 所示。其中网络有m个输入X,n个输出Y,j个隐含层神经元,其中1 ≤i≤m,其中1 ≤k≤n,wij为输入层与隐含层神经元连接权值,wjk为隐含层与输出层神经元之间的连接权值。信息通过输入层传递到隐含层,在隐含层变换处理后,到达输出层输出结果,则一次正向学习完成,当模型输出与期望输出误差未达到要求,则神经网络按照误差梯度下降的方法反向修正各层权值,即为误差反向传播过程,重复直至误差达到要求或学习超过最大次数阈值结束。
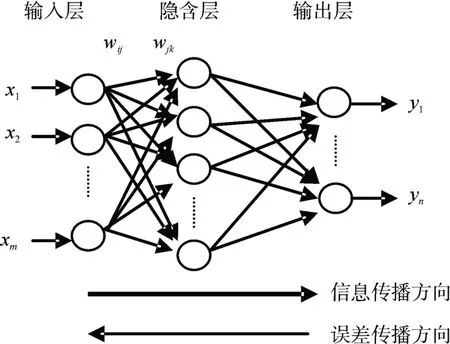
图1 神经网络模型图
2.2 类电磁机制算法
类电磁机制算法(Electromagnetislike Mechanism,EM)是S.I.Birbil 和S.C.FANG 在2003 年提出的,一种新的基于种群的元启发全局优化算法[12~14]。EM 算法模拟电磁场中电粒子吸引和排斥机制,把初始种群看作空间中的电粒子群,待优化目标函数的值看作电粒子的电荷量,由电荷量决定粒子受到其他粒子的吸引力和排斥力的大小,即目标函数值越小,粒子的吸引力越大。然后通过计算电粒子带电量和合力计算出粒子的移动更新规则,若干次迭代后得到全局最优解。EM原理三个粒子简化图如图2所示。
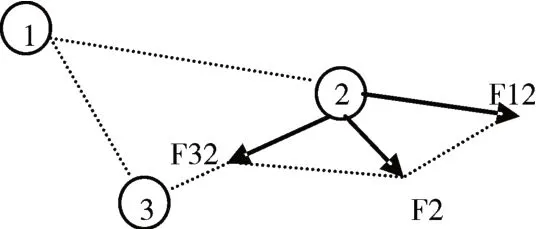
图2 EM算法原理简化示意图
在图2 中有三个电粒子,1 号的函数值大于2号,3 号的函数值小于2 号,所以1 号对2 号粒子表现为排斥力F12,3 号对2 号表现为吸引力F32,2 号受到的合力为F2,指向2 号粒子移动的方向。EM算法的收敛性已经得到充分证明,即迭代数次后,种群中至少有一个粒子会以概率1 移动到全局最优解的位置。
EM 算法简单有效,一般分四个步骤:初始化、局部搜索、电荷量与合力计算和粒子移动。EM 算法的实现伪代码如算法1所示。

2.3 改进类电磁机制算法
经典类电磁机制算法为通用计算平台设计,针对水质预测传感器端计算平台资源的约束,在初始化阶段,改进算法采用归一化方法,具体为最大最小归一化,缩小了计算数值的范围,从而有效地降低了运算复杂度。在计算合力阶段,引入一个合力计算修正因子,减小距离对预测结果的影响,可让网络模型避免出现早熟现象。具体改进公式如下。
1)归一化方法采用最大最小归一化(Min-Max normalization),公式表示如下:

最大最小归一化是对原始数据的一种线性变换,可以把结果映射到[0,1]之间。
2)将EM 算法计算两个不同粒子间合力的公式改进为
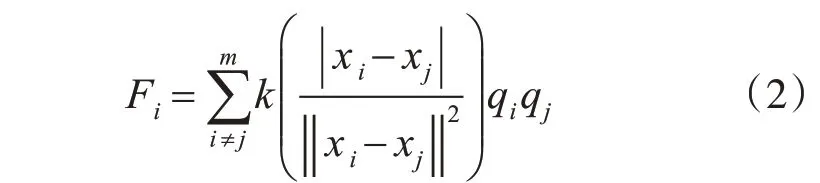
其中k为修正因子,通过对两个不同粒子的距离修正,强化粒子之间的作用力的强度,该参数可通过模型迭代学习获得。
2.4 改进类电磁机制算法优化神经网络模型
对多层网络模型,全局优化算法采用本文提出的改进EM算法,其流程如图3所示。
3 仿真实现
3.1 研究区域概述
黄河兰州段西起八盘峡,东至乌金峡,穿过兰州市区,是兰州工业用水和居民饮用水的唯一地表水源。每年由兰州市排入黄河的污水量约1 亿吨,其中生活污水为60%左右,主要污染物为挥发酚、氨氮、石油类、高锰酸盐[15]。近年来由于兰州市区沿黄河快速扩张,取水量和排污量增大,径流入水量天然减少,水体自净能力降低,导致黄河兰州段水污染问题非常严峻。黄河兰州段有5 个水质监测断面,从西至东断面名称与编号分别为1 号扶河桥(入境),2号湟水桥(支流),3号新城桥,4号包兰桥,5号什川桥(出境)。其中2号为省级断面,其余4 个为国家级断面,每个断面设置左中右三个采样点。黄河兰州段水域如图4(a)所示,水质监测断面概化图如图4(b)所示。
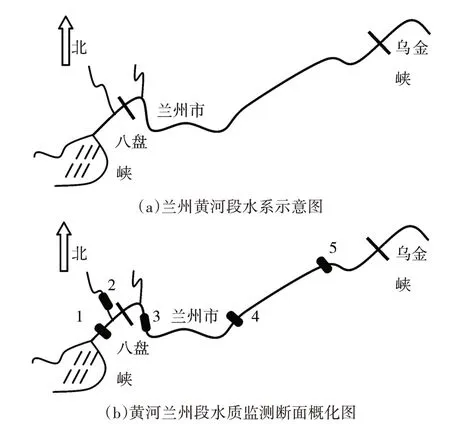
图4 兰州黄河段水系概化图
3.2 实验数据
本文水质预测的研究区域为黄河兰州段,数据源自中国国家环境监测数据中心和甘肃省环境监测数据中心。选择国家级检测断面兰州新城桥监测点2011年~2014年水质监测数据,每两周记录一次,共计177组。其中前154组数据为训练样本,其余23 组数据为测试样本。水质DO 值反映水质有机物污染的程度,是水生物主要的生存条件之一,也是衡量水质综合指标之一,与其他水质参数如PH 值,温度(T,摄氏度),总磷(TP,mg/L),总氮(TN,mg/L),总氨(T-Am,mg/L),总碱度(T-Alk,mg/L)等相关。所以本文以预测溶解氧(DO,mg/L)含量为例,其他水质指标与其预测原理类似。水质数据存储在Excle 中,在Matlab 中读取水质参数程序源码为

3.3 数据归一化处理
数据归一化Matlab程序源码如下:
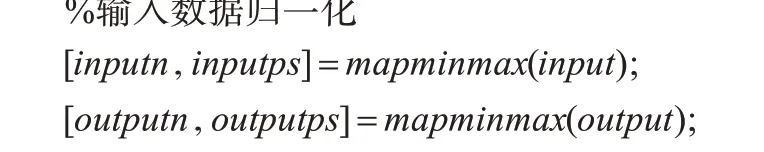
其中x 为变换前水质数据,y 为变换后数据,要求x 是有限实数值而且矩阵每行不全为0,变换后的数据在[0,1]区间内。仿真结束后,将网络输出变换为水质数据,Matlab程序源码如下:

3.4 算法实现
根据所建立的多层网络预测模型,网络结构实现的Matlab程序源码为

优化类电磁机制算法的参数设置,多次试验结果综合考虑全局最优解和迭代时间,种群规模选择10,进化代数选择5,根据网络结构计算出种群中每个粒子的长度为51,EM算法参数初始化为

EM 算法主程序部分根据图4 写出,考虑测试样本数量,为缩短迭代次数,可以选择不带局部搜索的EM 算法,所以定义局部搜索次数为零。算法还包括初始化,计算移动和计算合力三个函数。
4 实验结果分析与讨论
采用经典反向传播多层网络(BP)、遗传算法优化多层网络(GA-BP)和改进类电磁机制算法优化多层网络(EM-BP),对黄河兰州段新城桥监测断面水质数据进行预测,网络结构保持一致,预测溶解氧量,仿真结果均方误差曲线如图5 所示,训练结果曲线如图6所示,预测结果如图7所示。
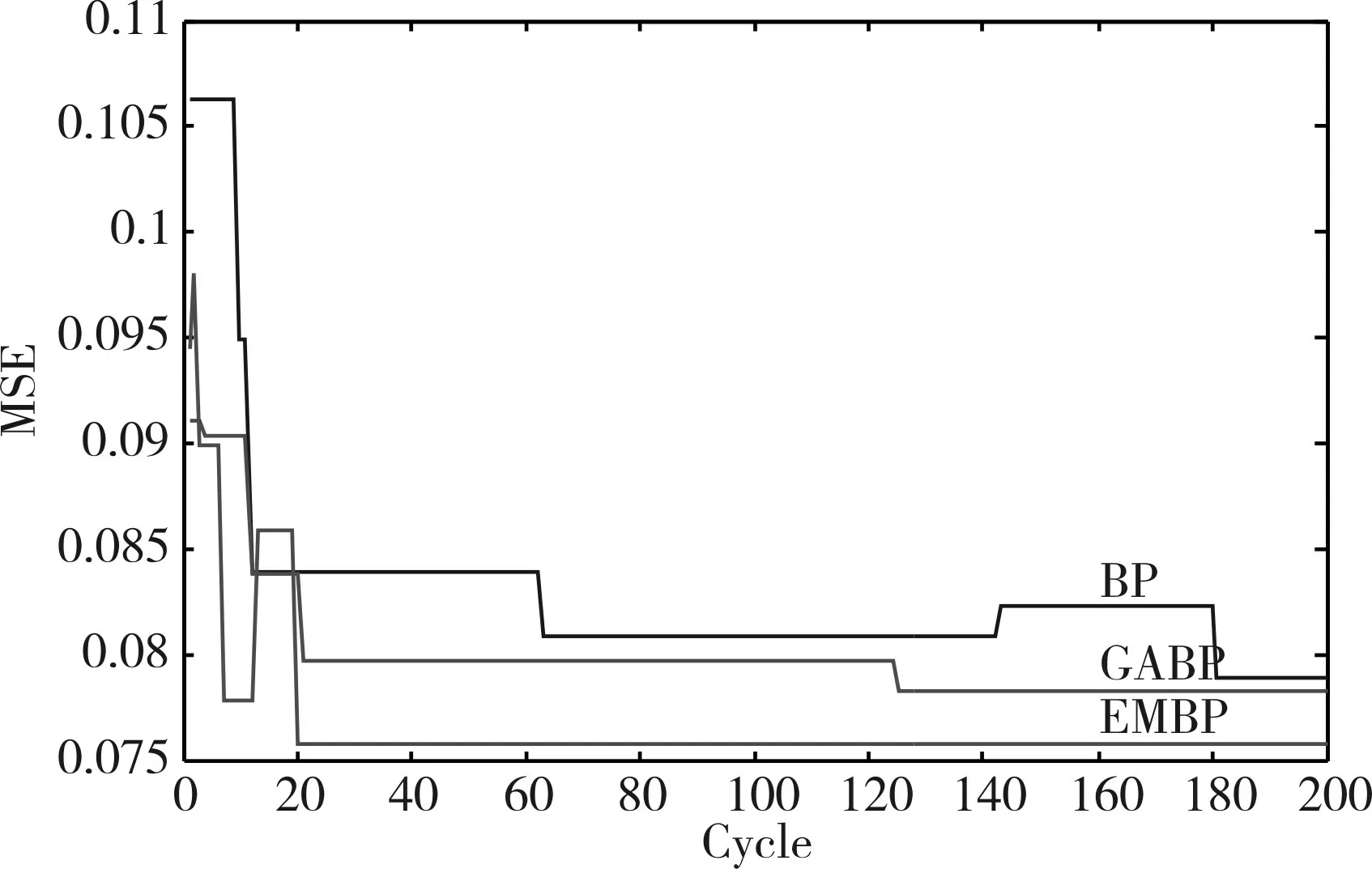
图5 均方误差曲线图
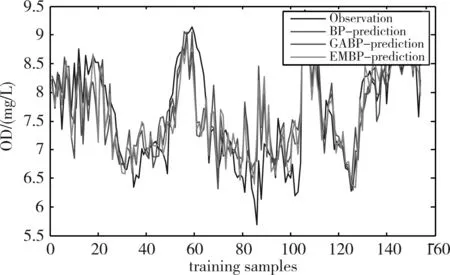
图6 训练结果曲线图
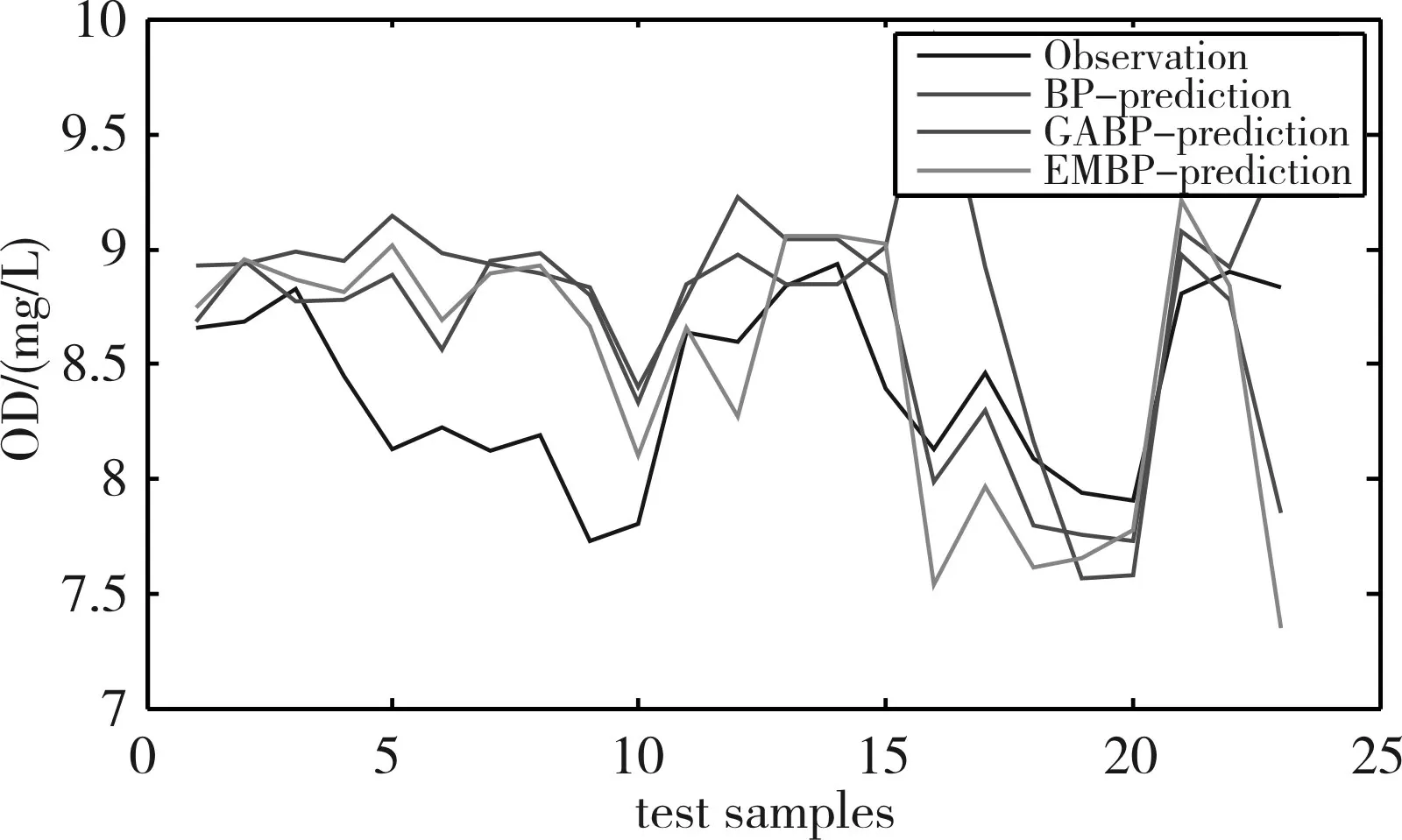
图7 测试结果曲线图
从图中可以看出BP 网络的均方误差较大,GA-BP 和EM-BP 的均方误差较小,在20 次循环后EM-BP 模型可以获得更小的均方误差和更好的误差稳定性。 为进一步证实EM-BP 模型的优越性,对GA-BP 和EM-BP 两个模型分别导入2014 年新城桥监测断面第14 周次至第23 周次的10 组水质数据进行仿真,仿真得到误差值如表1所示。
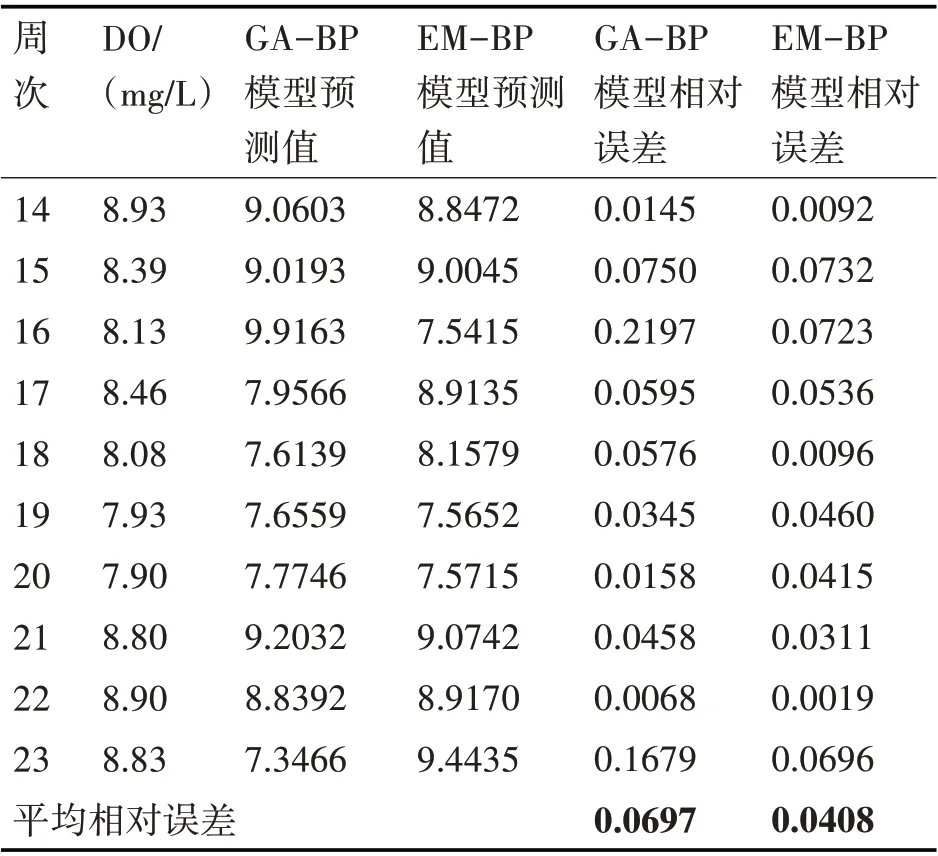
表1 EM-BP与GA-BP误差对比
分析表中数据得到,EM-BP模型相对误差8次小于GA-BP 模型相对误差,而且EM-BP 最大相对误差为0.0732,最小为0.0019,GA-BP 最大相对误差为0.2197,最小为0.0068,所以,EM-BP 模型的预测值相对更准确,相对误差较稳定,更适合水质预测。
5 结语
本文将改进后的类电磁机制算法与多层神经网络结合建立水质预测模型,将求解网络的各层权值和阈值转化为类电磁机制算法中粒子的吸引力和排斥力的计算,并以黄河兰州段监测断面水质数据为训练和测试样本,与经典BP 网络和GA-BP 网络对比仿真,在网络一致性前提下,三种方法均得到可靠预测结果。分析实验结果表明,引入改进EM 算法优化多层神经网络建立的水质预测模型,与传统方法相比,具有预测误差较小,误差较稳定和预测精度较高的特点。水环境是一个非常复杂的非线性系统,水质除了受到自然环境影响外,还会受到经济社会发展的影响,这使得水质预测存在很大的不确定性。而黄河兰州段因其特殊的地理和人文环境,水质的发展趋势与居民生活息息相关,因此,尽可能地接近未来水质的真实状况,需要更加成熟的预测模型。

