基于蝙蝠算法优化模糊神经网络的耙吸挖泥船耙头吸入密度研究

郝光杰 俞孟蕻 苏 贞

（江苏科技大学电子信息学院 镇江 212003）

1 引言

耙吸挖泥船疏浚施工过程中，泥沙依靠耙头挖掘产生，因此耙头挖掘效果直接影响到疏浚的生产效率［1］。耙头产量由吸入密度决定，因此对吸入密度建模分析尤为重要［2］。目前所知的耙头物理模型都基于一定的理想条件，例如保持土质类型不变，施工疏浚环境不变［3～4］。然而在实际施工中，同一地区土质类型多样，所面临的施工环境也不确定。因此通过物理建模难以建立有效的耙头模型。

文献［5］采用最小二乘法对吸入密度进行拟合，这种方法属于离线预测，不具有实时性。如果施工工况突然改变，这种测量手段失效。文献［6］采用遗传BP 对耙头建模分析，这种方法存在收敛速度慢，预测精度不高等缺点。

本文提出利用模糊神经网络（FNN）对耙头进行数据黑箱建模分析。模糊神经网络具有映射能力强、自学习及实时处理等优点，在轨道电路故障诊断［7］、配电网故障选线［8］以及高速行车时间预测［9］等领域效果明显。为了提高FNN 模型的泛化性能，有些文献采用粒子群算法［8］、遗传算法［10］对FNN 的连接权值和隐含层阈值进行优化。但是PSO 算法全局搜索能力有限，容易导致算法的复杂度提高；使用遗传算法容易产生早熟，局部最优等问题。在本文中采用蝙蝠算法［7］对FNN 进行优化，这种方法容易实现，与粒子群算法相比，结构简单，收敛性能更好。

2 耙头产量分析

2.1 疏浚数据分析

影响疏浚产量的因素一般可分为外界因素和内部因素［11］。外界因素主要为外界环境，例如风浪、沙床分布、土壤类型等［2，12］。内部因素耙头部分取决于耙头吸入密度，而吸入密度的大小又取决于高压冲水、泥泵转速、波浪补偿器行程等影响因子。根据施工人员现场经验与文献［13］，本文选择了以泥泵转速、航速、高压冲水与对地角度以及吸入流量5 个输入量对吸入密度进行建模预测，如图1所示。

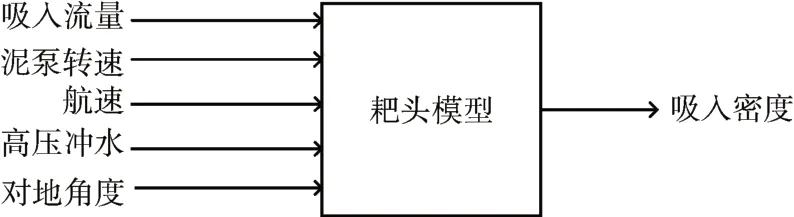
图1 耙头模型示意图

2.2 数据预处理

疏浚数据集为耙吸挖泥船从航行、挖泥装舱到抛泥整个流程，而我们所需的数据集主要集中在挖泥装舱阶段，需要对数据集进行有效整理，例如设置边界条件，考虑耙头吸入密度大于1 ton/m3以及正常施工时航速和泥泵转速的大小进行综合考虑，剔除无效数据。

施工数据采集于耙吸挖泥船各种不同的传感器和控制器，采集数据之间差异较大，量纲不一。为了避免数据大小对预测结果造成影响，对数据集进行归一化和标准化处理。

3 T-S 模糊神经网络

3.1 系统结构

T-S 模糊神经网络是一种if—then模糊规则来描述非线性系统的方法［7～8］，具体结构如图2所示。

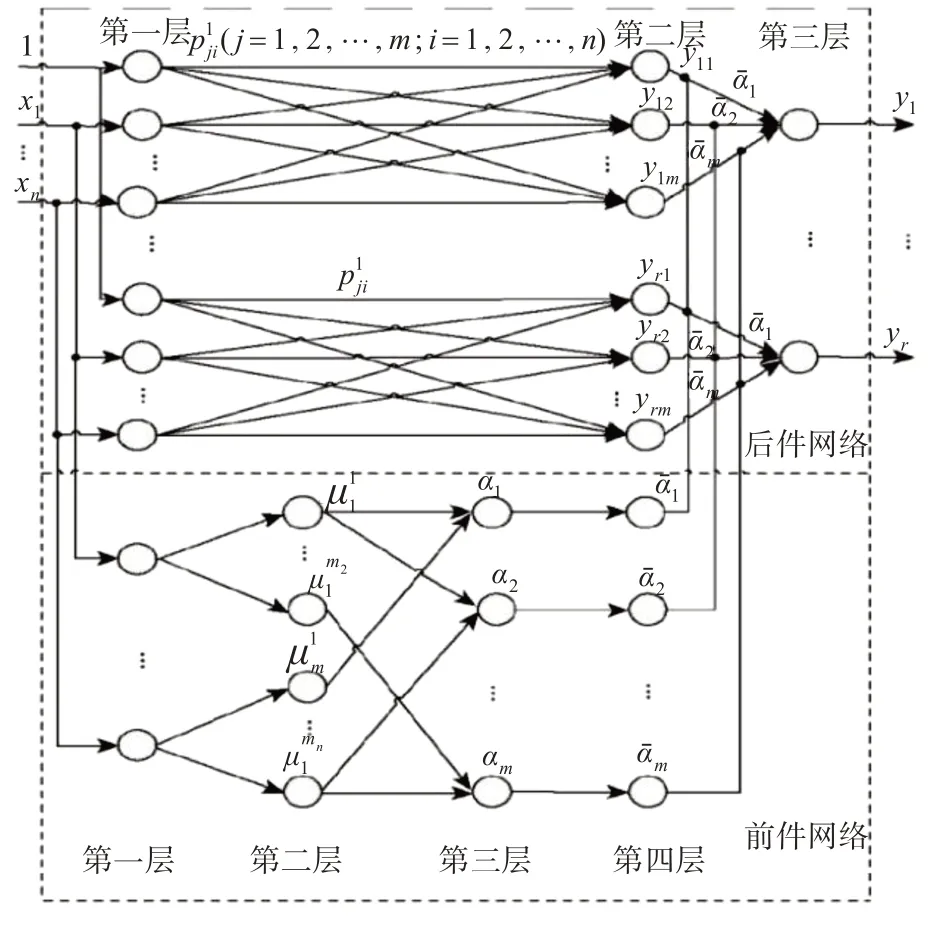
图2 T-S神经网络图

T-S 型模糊神经网络包括前件网络和后件网络。前件网络分为4 层，第一层是将输入量x=(x1,x2,…xn) 传送到第二层，该层节点数为N1=n。

式中，cij、σij为隶属度函数的中心与宽度。

第三层为规则层，节点总数为N3=m，每一个节点代表一条模糊规则，它是用来匹配模糊规则的前件，计算出每条规则的适应度，即

3.2 学习算法

式中β＞0为学习效率。

3.3 蝙蝠算法优化FNN模型构建

蝙蝠算法（BA）是一种高效的生物启发式算法，它的原理是模拟蝙蝠利用声呐来探测猎物［14～15］。这种算法全局搜索能力强，结构简单参数少，容易设置它的实现流程如下。

1）设置蝙蝠初始种群个数为n，最大脉冲音量为Amax，最大脉冲率为Rmax，搜索脉冲频率范围［Fmin，Fmax］，音量衰减率为β，搜索频率的增强系数为μ，最大迭代次数设置为Nmax。

2）随机对蝙蝠的位置Xi进行初始化，计算当前适应度的好坏来寻找最优解Xbest。

3）每一代蝙蝠个体的搜索脉冲频率、速度和位置按以下方式进行更新：

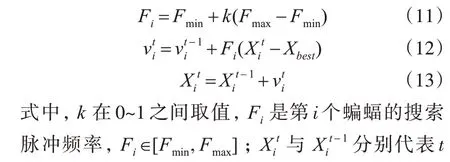
式中：β和μ的取值范围为（0，1），一般设置为0.9。

6）对n 个蝙蝠个体的适应度值进行排序，找到当前最优解。

7）重复步骤2）～6），直到满足最大的迭代次数，得到最优连接权值和隐含层阈值。。

4 仿真实验与分析

4.1 数据来源

实验数据来源于长江口施工，数据点每间隔30s 采集一次。对疏浚数据进行预处理，得到12 个周期共4300 条数据，将其中10 个周期作为训练数据，剩余两个周期的数据作为测试数据。图3 给出了一个周期原始吸入密度数据分布图，共300 个点，时间为150min；其中挖泥装舱阶段数据点分布在［50，240］，共190个样本点，时间为95min。

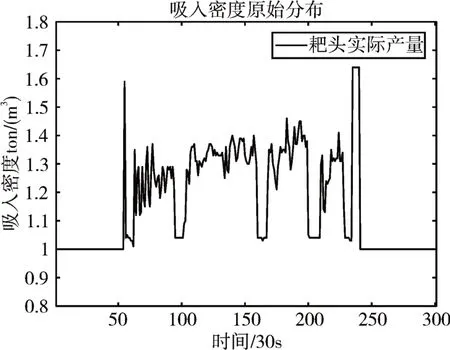
图3 原始数据分布图

为了使BA-FNN 耙头产量模型的预测性能更具有说服力，采用BP、FNN 进行实验仿真对比，并采用平均误差作为评价指标对预测结果进行衡量。

4.2 实验结果分析

实验中设置BP输入层神经元个数为5，隐含层神经元个数为12，输出层个数为1；模糊神经网络结构采用5-12-1，蝙蝠算法初始化种群为30，最大迭代次数设置为1000，蝙蝠脉冲响度Amax为0.6，最大脉冲率为Rmax为0.6，其中搜索脉冲频率范围设置为［0，2］。下面给出了两个周期吸入密度预测结果如图4、图5所示。

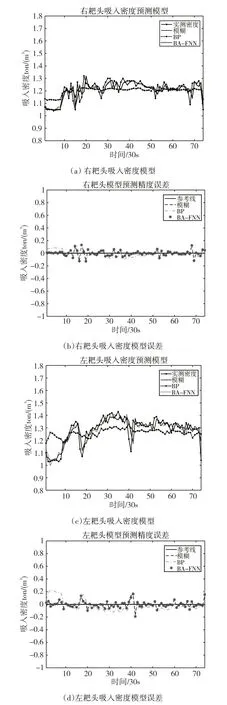
图4 周期1吸入密度预测

图5 周期2吸入密度预测

图4 为第1 个周期内3 种预测方法对左、右耙头产量进行预测的效果图以及误差对比图。第1周期为74个采样点，即耙吸挖泥船工作37min的耙头产量，从图4 中可以发现BP 神经网络的预测效果最差，FNN学习速度更快，泛化性能好于BP神经网络；通过对FNN 连接权值和隐含层阈值使用蝙蝠算法进行优化，FNN 预测效果得到了提升；在BP、FNN 以及BA-FNN 三者的预测效果上看，BA-FNN 预测效果相对于其他两种算法来说，预测效果更好，模型误差更小。图5 为第2 周期（一共70 个点，共计30min）耙头产量的预测效果图以及预测误差对比图。其中BP 预测效果不佳，预测误差也比较大，BA-FNN 预测效果比较明显。从实验训练时间来看，单个预测模型中BP用时最长，大约为900s，FNN 训练时间大约为560s；BA—FNN 的训练时间最短为435s。对3 种预测方法的平均误差进行统计，两个周期左、右耙头预测模型平均误差如表1所示。

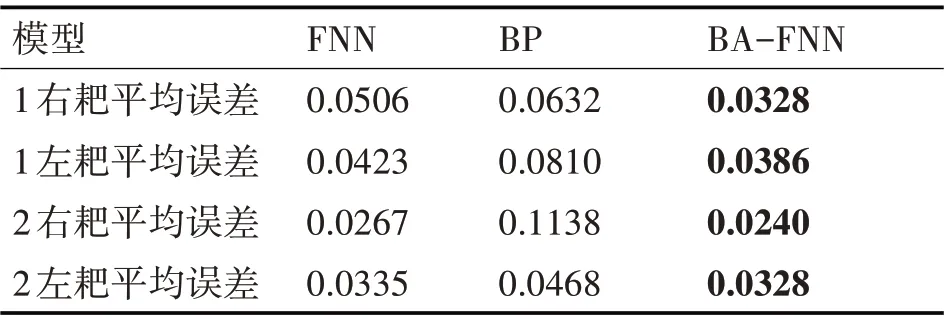
表1 各周期预测模型的平均误差

通过表1 可以看出，BA-FNN 的平均误差最小，预测精度高，经过上述两个周期的验证分析，结合实际的疏浚施工经验，上述BA-FNN预测模型产生的误差满足在疏浚要求的合理范围之内，因此该方法可运用于耙吸挖泥船耙头模型吸入密度的预测。

5 结语

1）使用蝙蝠算法解决了传统神经网络收敛速度慢，预测精度低的问题，优化T-S 模糊神经网络的参数，得到了T-S 模糊神经网络参数最优组合，克服了传统模糊神经网络参数确定难度大的问题，改善了模糊神经网络的泛化能力和自学习能力。

2）针对耙头产量进行分析，对吸入密度进行预测，并且借鉴于以往的研究成果，提出了蝙蝠算法优化T-S 模糊神经网络的方法对耙头吸入密度进行预测。实验结果表明采用BA-FNN 具有收敛速度快，预测精度高的优点，该方法在输出稳定性、收敛性和预测精度上也优于T-S 模糊神经网络。证明了采用BA-FNN对吸入密度预测精度更好，并验证了该方法在耙吸挖泥船耙头中预测吸入密度的可行性。该方法可以作为耙头产量吸入密度预测的一种技术手段，并为耙吸挖泥船耙头产量分析提供了一种科学有效的方法。