基于Adams-Bashforth-Moulton 预估校正法的NURBS 插补算法研究*
李钱宽 张永林
(江苏科技大学 镇江 212003)
1 引言
高速、高精、高质量的复杂曲线曲面加工技术在航空航天、精密仪器等行业中有着非常重要的国家战略意义[1]。NURBS(Non-Uniform Rational BSplines)曲线在复杂工件几何形状的描述和控制上具有优异的表现能力。随着工件型面复杂度和加工精度需求的提高,传统直线插补的方法已经无法满足加工要求,NURBS 曲线直接插补是目前最有效的解决方法[2~3]。
目前,NURBS 曲线插补中应用最广泛的是Taylor级数展开法[4~5],此方法虽然可直接得到插补点参数,但在计算时需要求取插补曲线的一阶导数和二阶导数,计算繁杂,影响算法的实时性;而且截断误差较大,当増加保留项数时,可降低截断误差,但计算量会大幅增大。
为解决这种问题,国内外学者提出基于“预估-校正”的新算法[6~10],通过二阶Taylor 展开法或Adams 微分方程预估插补点参数,进而计算实际步长与理想步长间偏差,以降低该步长偏差为目标,迭代反馈校正参数值,使实际加工步长与理想值间偏差小于设定的约束极限。
为了提高NURBS 曲线插补参数计算的准确性,降低插补过程中的速度波动,本文在以上研究的基础上提出了一种基于Adams-Bashforth-Moulton(以下称ABM)预估-校正的NURBS 插补算法。通过分析NURBS 曲线插补算法的原理,首先考虑插补速度规划,在弓高误差和进给方向加速度的约束下计算期望步长;然后在插补速度波动的约束下利用Adams-Bashforth-Moulton 预估校正法得到下一点插补参数。最后使用Matlab 仿真平台进行了仿真实验。
2 NURBS曲线插补算法
2.1 NURBS曲线的定义
一条有n+1 个控制点的k次NURBS 曲线的有理分式定义为

2.2 插补速度约束
插补过程中不仅需要对误差进行控制,还需要保证插补速度的平稳性。NURBS 曲线插补进给速度vi主要受到以下条件约束:最大弓高误差emax、最大法向加速度aNmax、最大法向加加速度JNmax及指令速度Fmax[13]。
1)弓高误差条件约束
采用圆弧近似法计算弓高误差。如图,首先计算当前插补点Qi处的曲率半径ρi,计算公式为

2)机床动力学参数条件约束
设插补点Qi处的曲率半径为ρi,给定最大的法向加速度aNmax,最大法向加加速度JNmax,则在法向加速度和加加速度约束下,插补点Qi处的最大进给速度分别为

3 基于Adams-Bashforth-Moulton法的预估校正算法
3.1 基于Adams-Bashforth-Moulton 法的参数预估
基于Adams-Bashforth-Moulton 法预估校正算法预估下一点插补参数。结合了显式的四步四阶Adams-Bashforth 方法和隐式的三步四阶Adams-Moulton方法进行预估计算,方法如下[14]:
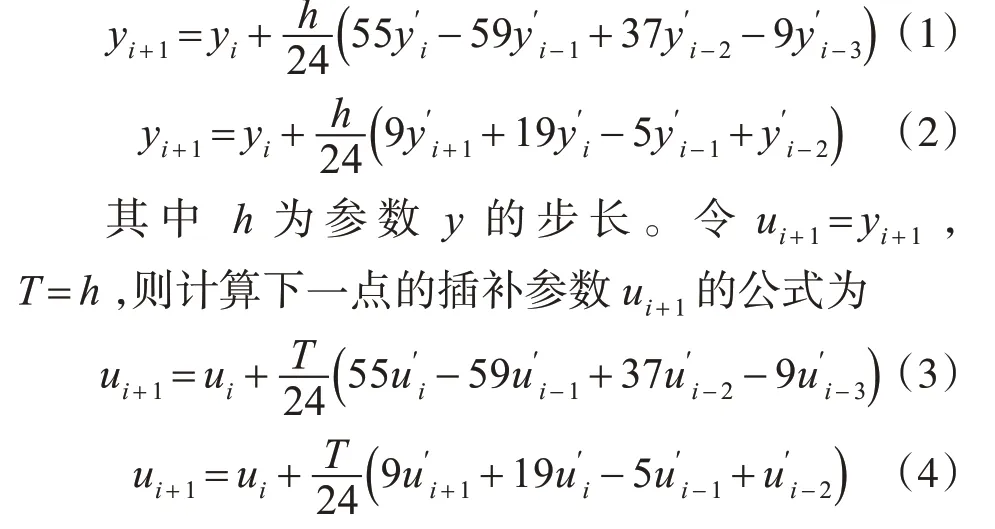
由于同阶的隐式方法比显式方法的截断误差更小,所以使用式(3)计算ui+1能获得更准确的计算结果。

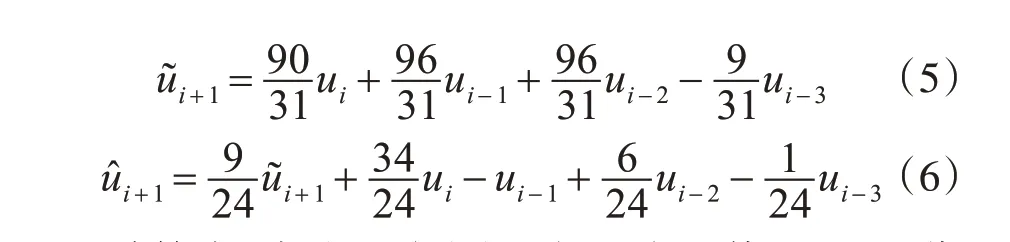
计算中,先按照式(5)进行一次预估,然后再代入式(6)进行一次校正,从而得到较为精确的预估值ûi+1。
得到预估值后对其进行校正,以预估步长和期望步长之差为指标。校正之前依次计算期望步长和预估步长,计算预估步长采用预处理矩阵法[15],计算期望步长采用速度约束进行规划。
3.2 基于速度波动控制的插补参数校正
根据以上计算得到的当前点插补最大进给速度和插补周期可以得到预估插补步长Li=viT,构造关于插补点参数的速度波动函数[15]:

ui+1,k是第k次迭代之后的计算参数值,ui+1,0=ûi+1。为尽可能提高计算效率,使用Steffensen 法简化求导[16],用差商形式替代导数得到插补参数迭代计算式为

4 仿真验证
为验证本文所提出的插补算法的有效性和准确性,采用Matlab 平台对NURBS 曲线进行仿真分析。为体现本文算法的优越性,在仿真中与传统基于Taylor 展开式及文献[7]所提的NURBS 曲线插补算法进行对比分析。仿真曲线参数如表1 所示,曲线轨迹如图1所示。

表1 NURBS曲线参数

图1 插补曲线轨迹
设定的曲线插补参数如表2所示。

表2 曲线插补参数
选定速度波动率ε作为算法的评价标准,分别采用二阶Taylor 展开法、文献[8]中提出的Hamming预估法和本文所提算法进行仿真对比,采用本文的迭代方法,仿真结果如图2~图4所示。
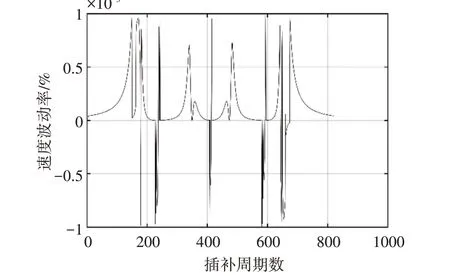
图2 二阶Taylor展开法速度波动率

图3 Hamming预估法速度波动率
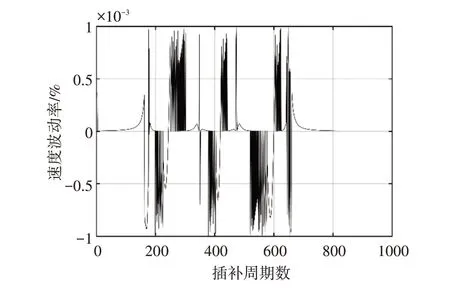
图4 本文ABM预估法速度波动率
可见三种方法的速度波动率都被控制在限定值以内。为了较好的分析,采用速度波动率平均值作为直观的评价指标[17]。
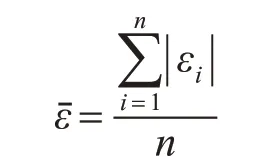
n为插补周期数,各方法结果为表3所示。
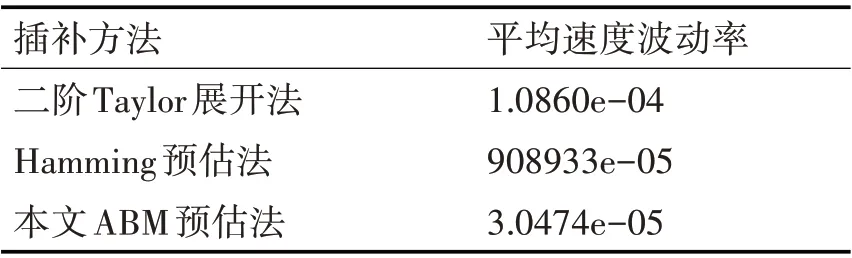
表3 各方法速度波动率平均值
由结果可知,本文提出的算法相较于二阶Taylor 展开法和文献[8]所提算法在速度波动率控制方面具有更优越的表现。
5 结语
本研究提出了基于Adams-Bashforth-Moulton法的插补参数预估校正算法。该算法首先进行插补速度规划,在弓高误差和进给加速度的约束下计算期望步长;基于Adams-Bashforth-Moulton预估校正法得到下一点插补参数预估值,并在速度波动控制下采用Newton-Rapson 迭代法进行插补参数校正得到最终参数值。
仿真结果表明,预估参数计算精度高,插补准确性高,在速度波动率控制方面具有更好的效果。

