随机模拟在预测混合丸剂均匀度中的应用
霍志鹏,寿纪纲,王 玉,何 毅
(1.天士力医药集团股份有限公司研究院,创新中药关键技术国家重点实验室,天津 300410; 2.天津中医药大学中药学院,天津 301617; 3.中国药科大学中药学院,江苏 210009; 4.天津大学药物科学与技术学院,天津 300072)
混合为药品生产中常用的操作,混合后的均一性为药品质量特性之一。通常认为粉体和颗粒容易混合均匀,丸剂混合后均匀度较差,均一性不合格的风险较高。丸剂混合也是药品研究和生产中可能遇到的情景,例如将速释微丸和缓释微丸混合填充制备缓释胶囊[1-2],丸剂的临床研究中低剂量组为了患者服用方便和降低破盲风险,可设计为真药和安慰剂混合包装成1 袋或一瓶。然而关于丸剂混合操作是否可行,以及混合均匀度的影响因素仍少见报道。本文采用数学建模中的随机模拟(蒙特卡罗)方法[3],对混合比例和单剂量包含丸数对混合均匀度的影响进行了模拟,以期为丸剂混合相关的生产提供参考。
1 方法
1.1 数学建模 药品的含量和含量均匀度为药品质量控制的关键属性,对于常规口服固体制剂,通常要求抽取10 个单剂量时,A+2.2S≤15(A 为单剂以标示量为100 的相对含量xi均值与100 差值的绝对值,S为标准差)[4],当均值与标示量相等时,A 值最小为0,2.2S≤15,则标准差 S 应≤6.8(15÷2.2 的近似值),即相对标准偏差RSD 小于6.8%,当均值与标示量不等时,则要求更低的RSD。
对于混合填充的丸剂产品,最简单的生产方式为将两种或多种药丸混合后分剂量包装,假设一产品由X、Y 两种药丸按固定比例混合均匀,X 药丸比例为p,单剂量的总药丸数量为n,单剂量含X 药丸的数量为k,则根据排列组合原理,单剂量中出现X 药k 丸的可能为为二项分布特征。该模型为理想模型,可预测药品含量的分布情况,可给出理论相对标准偏差RSD 的期望,但不能给出相对标准偏差RSD 的分布情况。
单剂量中X 药的含量具有随机性,随机模拟方法又称蒙特卡罗法,是基于随机过程发生的原理对复杂系统进行模拟的方法,可通过简单的算法,产生大量随机数,模拟事件发生的概率和分布情况[3,5]。通过对模拟抽样的统计处理,能同时得到样品含量和变异系数的概率分布情况,可解决上述理想二项分布模型的不足。
1.2 算法 丸剂混合包装的随机模拟算法流程图见图1,采用类似于掷骰子的方法产生随机数,根据随机数出现的区间和药丸的理论比例,逐个产生一粒X药或Y 药,直到产生一个单剂量的总药丸数。通过循环套嵌设置每轮抽样次数、抽样轮次,按含量均匀度抽样要求,抽样次数可设为10,即一轮抽样产生10 个单剂量,进行多轮次的随机模拟,对模拟数据进行统计处理得到每轮次抽样的含量、含量均值和RSD。通过调整每袋总丸数n 的数值,和X 药与Y 药的比例,可预测单剂量总丸数和两药的比例对含量和RSD 概率分布的影响。
1.3 算法实现 按图1 的算法使用Python 3.8 软件的random 库随机函数产生随机数,使用numpy 库中的数组数据类型对产生的抽样进行存储,numpy 库中统计函数对模拟数据进行统计处理。代码在安装Windows 10 系统的 PC 机(处理器:Core i7 8550U 四核 1.80 GHz,内存:8 G)上运行。
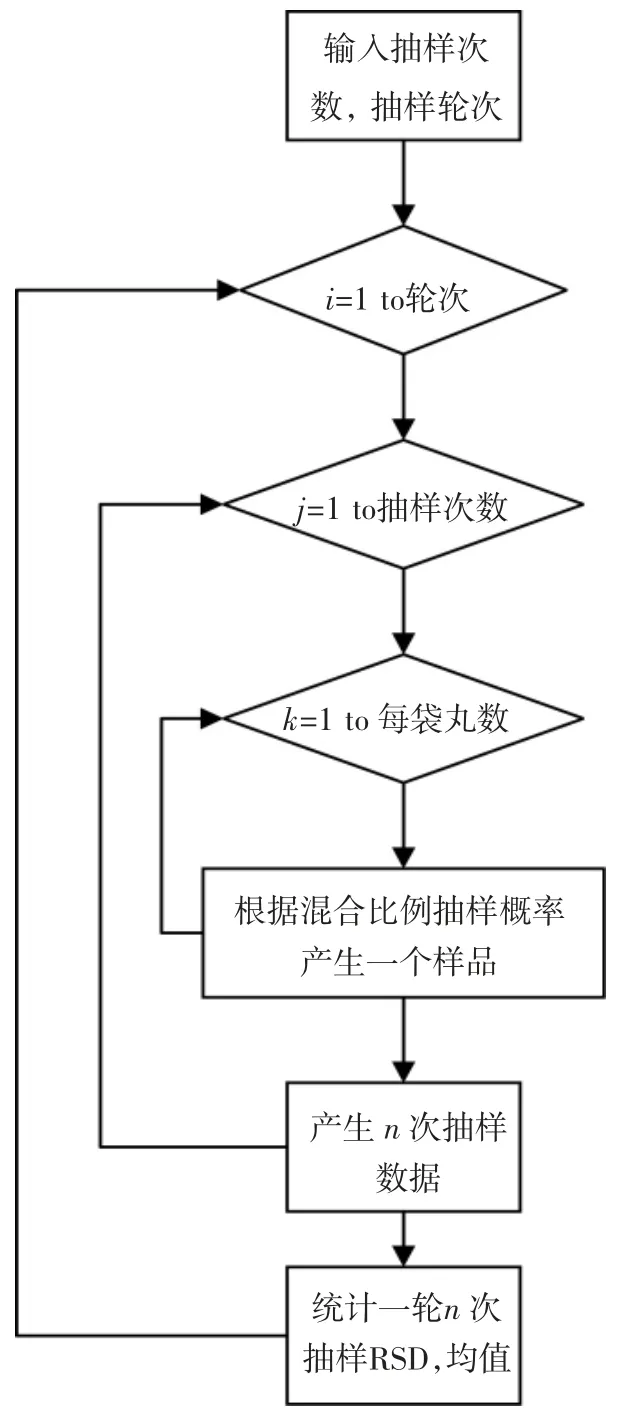
图1 丸剂混合分装的随机模拟算法图
2 结果
2.1 抽样轮次对模拟结果的影响 对单剂量含100 丸,X、Y 药丸1∶1 比例,采用上述随机模拟方法分别进行了 100 次,1 000 次,10 000 次和 100 000 抽样模拟。对产生数据按真药比例从0%到100%等分为100 个区间进行频数统计,与理论二项分布的频率分布进行比较,结果见图2。当样本数较少时,模拟抽样的频数分布与理论二项分布差异较大(图2 A),随抽样次数的增加,差异减小,当抽样次数达到100 000 次时,频数分布趋势线基本一致。
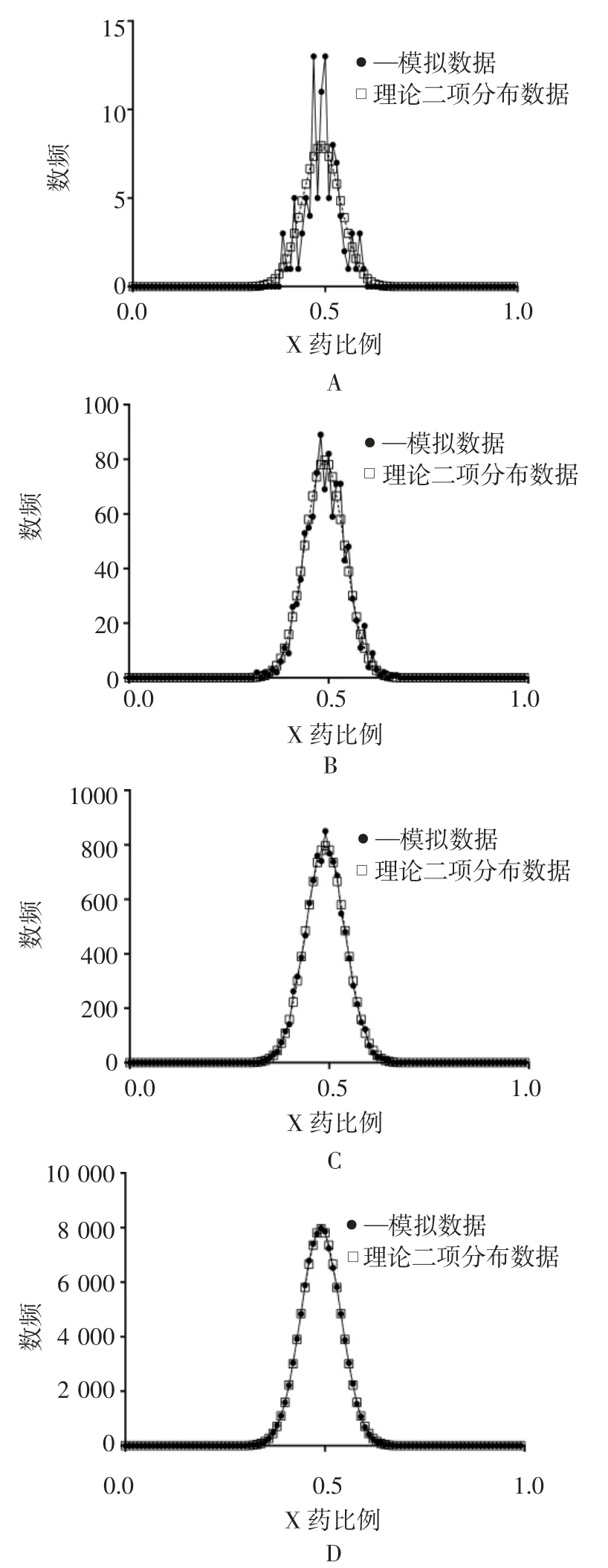
图2 100 次抽样(A)1 000 次抽样(B)10 000 抽样(C)100 000 次抽样(D)概率分布与理论二项分布比较
2.2 单剂量丸数和混合比例对相对含量分布区间的影响 分别对 X、Y 药丸 1∶1 和 2∶1 混合药丸,单剂量包装为 50、100、200 和 400 丸进行了 100 000 次的随机抽样模拟,单剂量中X 药比例的频数分布统计见图3 和图4,各随机模拟数据的整体频数分布与二项分布基本一致。从图中可见随着单剂量的丸数增加,X 药的相对含量分布区间变窄。化学药制剂一般控制含量在95%~105%或90%~110%,本研究统计了X 药在相对含量±10%区间累积频率,结果见表1 和表2。随单剂量丸数增加±10%区间累积频率增加;X、Y 药丸 2∶1 比例相对于 1∶1 比例±10%区间累积频率更高,1∶1 比例时单剂量到400 丸含量±10%的概率能到 95%以上,2 ∶1 比例时单剂量 200 丸含量±10%的概率即能到95%以上,单剂量100 丸和50 丸时含量超出±10%区间的概率较高。
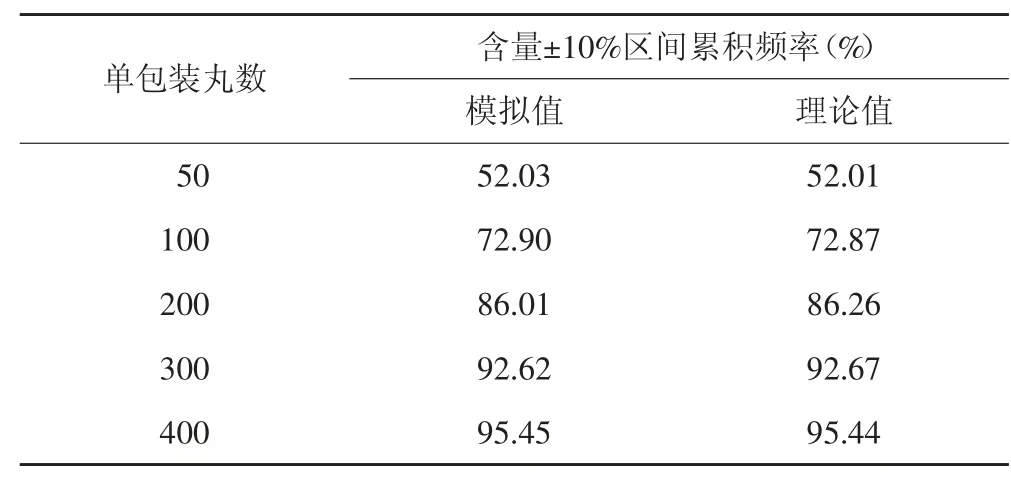
表1 X-Y(1∶1)单剂量不同丸数抽样含量在±10%区间的累积频率与理论值比较
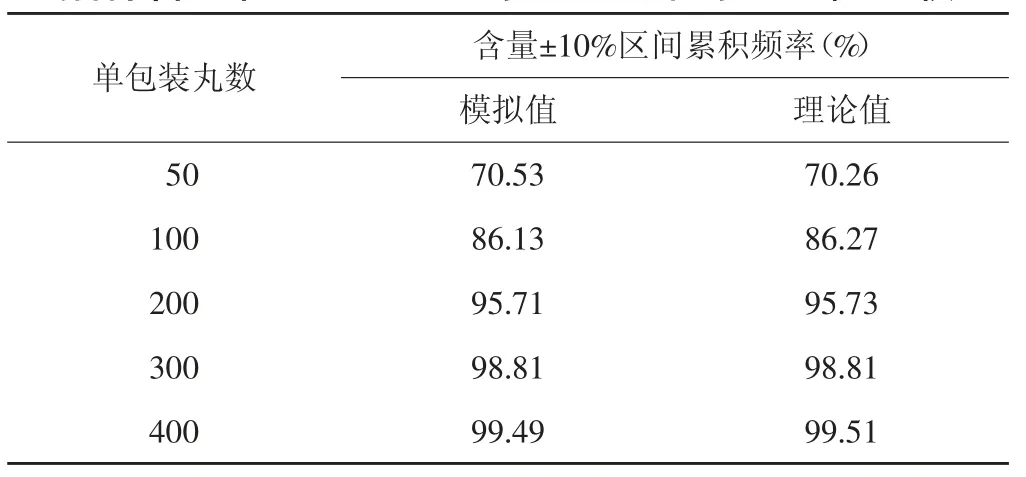
表2 X-Y(2∶1)单剂量不同丸数抽样含量在±10%区间的累积频率与理论值比较
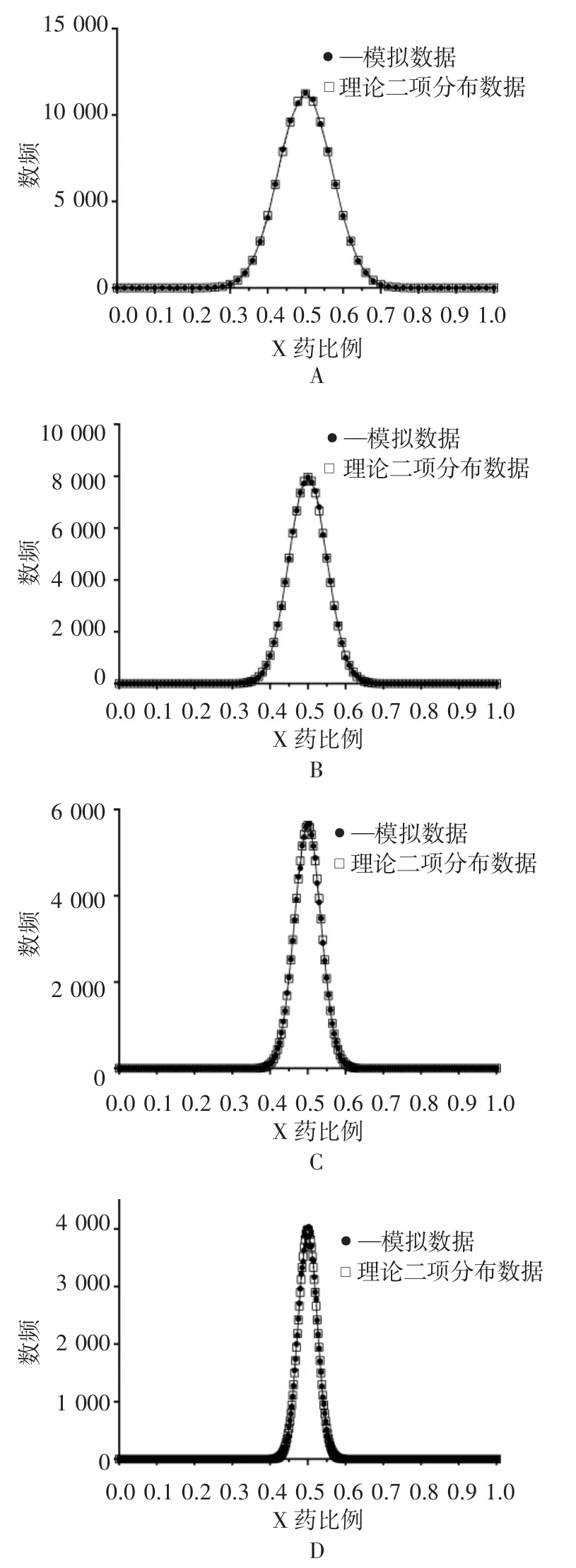
图3 X-Y(1∶1)单剂量 50 丸(A)100 丸(B)200 丸(C)400 丸(D)抽样模拟的 X 药含量分布
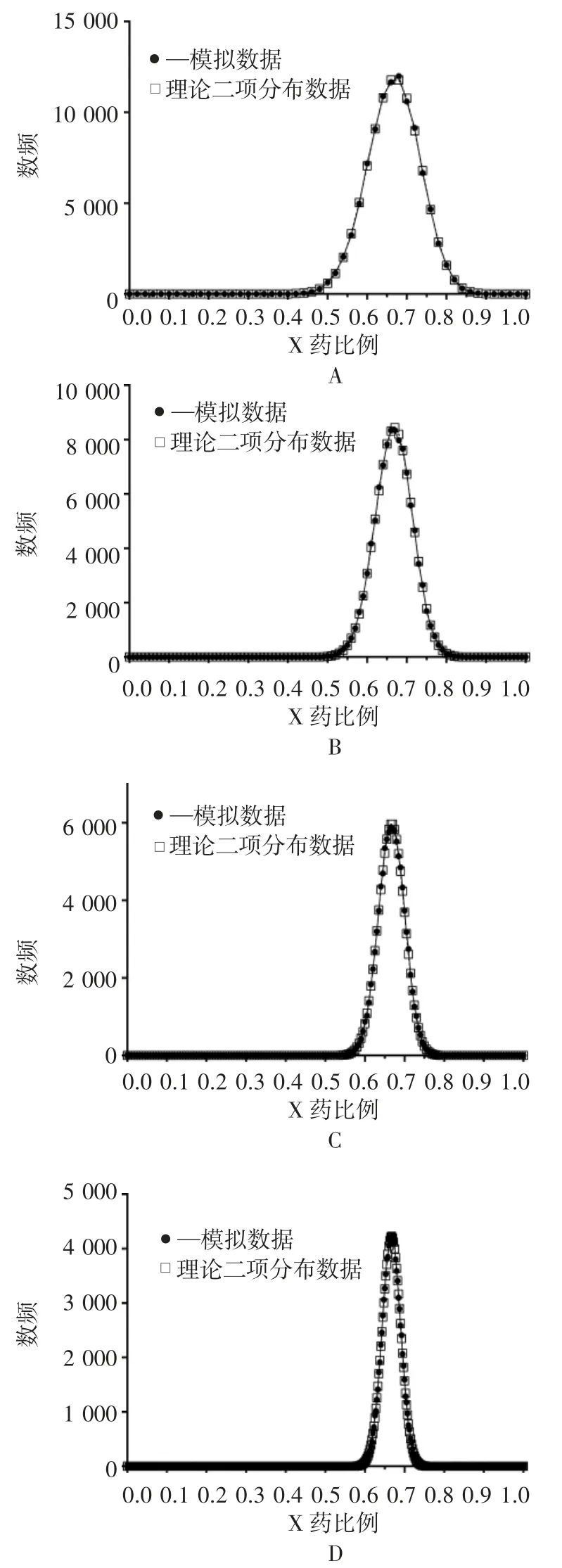
图4 X-Y(2∶1)单剂量 50 丸(A)100 丸(B)200丸(C)400 丸(D)抽样模拟的X 药含量分布
2.3 单剂量丸数对含量RSD 分布的影响 多次抽样的RSD 一定程度上反映了总体的变异,也是工厂生产和监管部门抽检时可监控的反映含量均匀度的指标。《中国药典》通则0941“含量均匀度检查法”要求检测10 个单剂量的含量的相对于标示量的变异。本研究用随机模拟法对X、Y 药1:1 比例和2:1 比例混合后分装药品抽样的RSD 进行了模拟,以10 次抽样为一轮,产生10 000 轮的数据,模拟抽样的RSD 概率分布见图5 和图6,图中用竖直虚线标出了RSD=6.8%的位置,按通则规定A+2.2S≤15 则供试品含量均匀度符合规定,为了简化模型,当抽样均值和理论均值相等时,只用2.2S 评价均匀度,2.2S≤15 可近似的转化为RSD<6.8%。
从图5 和图6 可见RSD 的总体分布范围随单剂量丸数的增加移动向更小的值,分布区间变窄,RSD<6.8%的累积频率增加。表3 统计了不同丸数的X 药含量 RSD < 6.8%的累积频率,X、Y 药 2∶1 比例随丸数增加更快的收缩向<6.8%的区间。
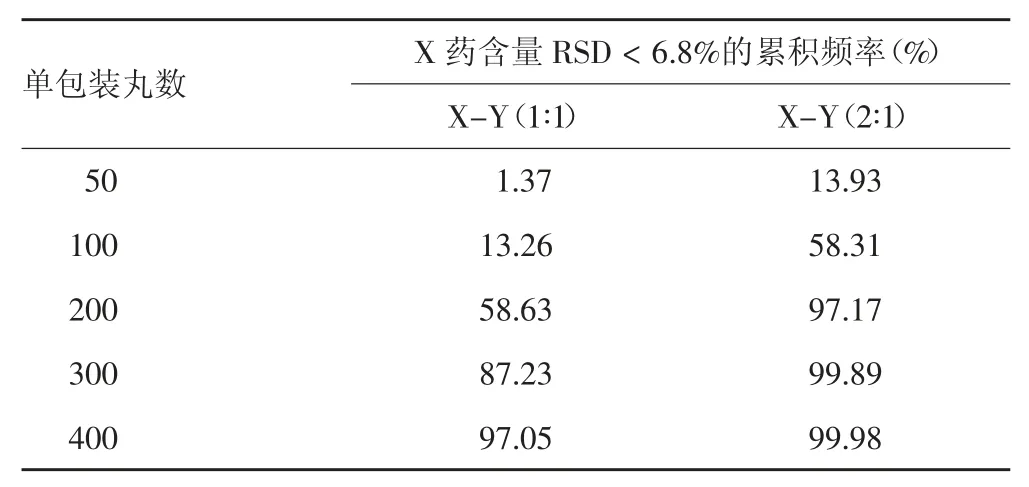
表3 单剂量不同丸数的X 药含量RSD<6.8%的累积频率统计
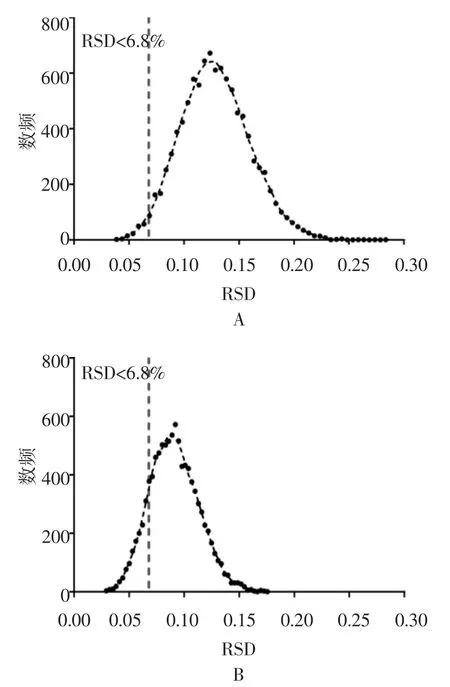
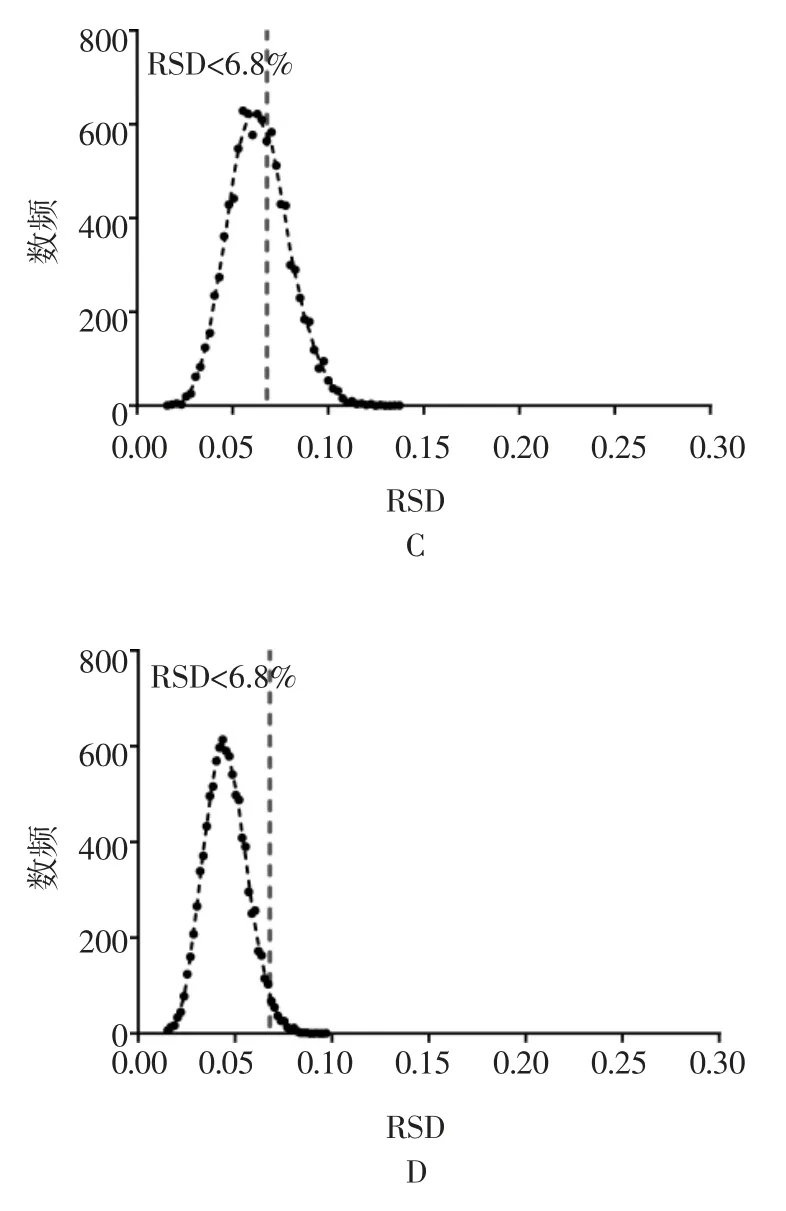
图5 X-Y(1∶1)单剂量 50 丸(A)100 丸(B)200 丸(C)400 丸(D)抽样模拟的 X 药含量的RSD 分布(圆点为频数数据,虚线为平滑连接线)
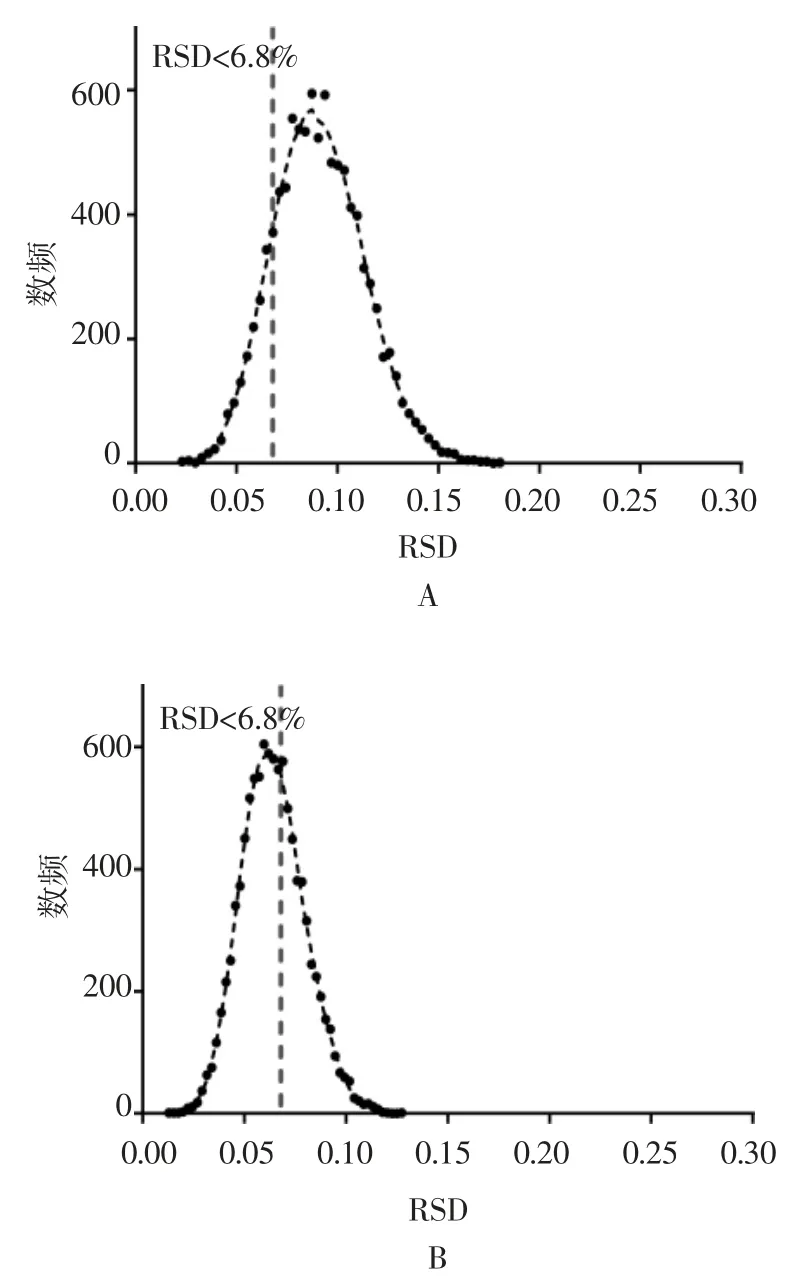

图6 X-Y(2∶1)单剂量 50 丸(A)100 丸(B)200 丸(C)400 丸(D)抽样模拟的 X 药含量的RSD 分布(圆点为频数数据,虚线为平滑连接线)
3 讨论
本研究建立了两种药丸混合后单剂量分装的随机模拟方法,可用于模拟单剂量包装中某一种药丸比例(含量)的概率分布和抽样的RSD 概率分布,为丸剂混合分装工艺是否可行提供参考。相对于人工只能一小时抽样检测几十个至上百个样品,基于计算机运算的随机模拟能在1 min 产生上万次的抽样数据,能快速的产生大量的数据,有助于快速了解事件的概率分布特征[6]。
本研究建立的模型根据概率分布,随机产生单剂量药丸的组成,模拟了从混合后的总体中分装到单剂量的过程。实际生产过程中影响含量均匀度的因素还有装量差异,不同药丸比重和摩擦力差异导致的分布差异。根据误差传递累积原理[7],这些因素将导致抽样的变异增加,即RSD 的增加。本研究模拟的为理想状态下概率分布和变异,实际生产中根据可能存在其他误差项,变异会稍有增大,因此本模型可提供复合丸剂分装单剂量的含量均匀度最保守的失败概率,实际的失败概率会稍高于预测值。
粉体和颗粒剂可看做由众多细小的颗粒(微粒)组成[8-9],本文建模的结果的也能一定程度上解释为什么颗粒剂和粉体比丸剂更容易混合均匀:同样重量的药品,粉体和颗粒包含的颗粒(微粒)数量一般远大于丸剂,单剂量内组成颗粒越多,其相对含量分布的区间越窄。从上文随机模拟数据可见,当一种成分占总体比例小时,其分布更宽,抽样的变异更大。这也从随机现象和概率分布的角度解释了药物制剂中随着主药含量占制剂比例的减少,含量均匀度风险升高这一现象[10-11]。《中国药典》通则0941 要求主药含量小于每一个单剂重量25%者应检查含量均匀度[4]。随着对粉体和颗粒性质的进一步了解,数学建模结合计算机模拟将有望解决固体制剂生产中更多的问题。
本研究探索了将随机模拟用于解决药品生产中的问题。对事件的数学本质进行分析,科学合理的建立数学模型,采用计算机强大的运算能力进行模拟,有助于预测相关工艺的可行性,为决策提供参考。

