传输密度的Lp,q估计

陈 平

(江苏第二师范学院数学与信息技术学院,江苏 南京 210013)

在欧氏空间中,与费用函数为欧氏范数|x-y|时的最优计划γ有关的传输密度σγ,其本质上可以视为欧氏空间Rd上的测度.可以证明作为测度,σγ关于Lebesgue测度是绝对连续的,从而其密度函数α(x):Rd→[0,+∞)存在,此外关于σγ的正则性也就是α(x)的正则性的研究可参考文献[1-4].在实际应用问题中,传输密度与图像处理有关,还可以用来描述和解决交通拥堵问题,上述研究结果可详见[1,5-6].本文主要研究了与费用函数为严格凸范数‖x-y‖时的最优计划γ有关的传输密度σγ,首先建立了σγ的等价定义公式以及σγ与位移内插μt的关系不等式,然后研究了位移内插μt的正则性,最后基于上述两个结论得到了σγ的绝对连续性和Lp,q正则性,这里p∈[1,+∞),q∈[1,+∞).由于欧氏范数|x-y|也是一种严格凸范数,从而,我们的结果推广了[1,2,4]中的关于σγ的绝对连续性和正则性的结论.

1 预备知识

定义1[5-6]设X为任意测度空间,对于给定的映射T:X→X以及μ∈P(X),T#μ给出了X上的一个概率测度,其定义为(T#μ)(A)=μ(T-1(A)),其中A⊂X为任意Borel集合.

定义2[5]设Ω⊂Rd为紧凸子集,μ,v为Ω上的概率测度,记为μ,v∈P(Ω),对于给定的c(x,y):Ω×Ω→[0,+∞),变分问题

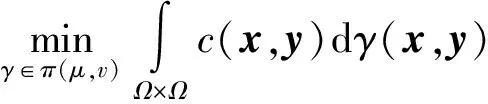
(1)

的解γ称为费用函数为c(x,y)时的最优计划,其中集合π(μ,v)中的元素γ称为运输计划,其定义为π(μ,v)={γ∈P(Ω×Ω):(π1)#γ=μ,(π2)#γ=v},这里π1(x,y)=x,π2(x,y)=y分别为对第一和第二变量的典范投影.

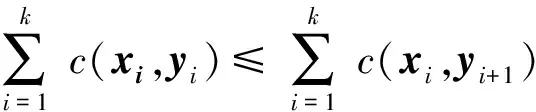
引理1[5-6]如果费用函数c(x,y)是下半连续的,且最优费用(1)是有限的,则γ是最优运输问题(1)的解当且仅当γ集中在c-循环单调集合Γ⊂Ω×Ω上,即γ(Ω×ΩΓ)=0.

定义4[3]设γ为费用函数为‖x-y‖时的最优计划,则可以如下定义Ω上的一个测度σγ:

(2)

其称为由γ诱导的传输密度.其中ωxy(t),t∈[0,1]为连接x,y的经由‖x-y‖定义的参数化测地线.

2 传输密度的Lp,q正则性

本节我们首先给出传输密度σγ的一个经由位移内插μt表示的等价定义公式,然后基于这一等价公式,以及对位移内插μt的Lp,q正则性的估计,建立传输密度σγ的Lp,q正则性估计不等式.在本文中p∈[1,+∞),q∈[1,+∞).

我们首先给出Lorentz空间及其上Lp,q拟范数的定义,可以看出Lorentz空间是Lp空间的推广.

定义6[2]Ω⊂Rd上的Lorentz空间是指由Ω上的Lp,q拟范数有限的全体可测函数,其中Lp,q拟范数定义为

由定义可知Lp,1(Ω)⊂Lp,p(Ω)=Lp(Ω)⊂Lp,∞(Ω)以及如下的Minkowski不等式成立:

定理1设γ费用函数取‖x-y‖时的最优计划,则由γ诱导的传输密度σγ可以表示成

(3)

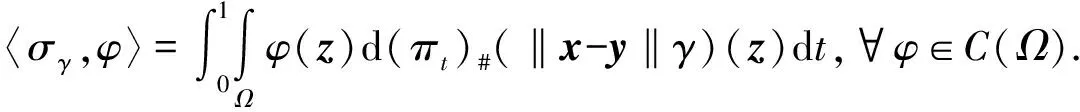
(4)

这里C=max{‖x-y‖:x,y∈Ω}>0为常数,μt=(πt)#γ,t∈(0,1)称为由γ诱导的从μ0=μ到μ1=v的位移内插.

另一方面,

从而式(3)成立.

最后,由于Ω是紧集以及位移内插μt的定义,再由式(3)可以得到式(4).

接下来我们讨论位移内插μt的正则性,可参阅[7-9].

(2)如果还有μ∈Lp,q,则μt∈Lp,q,且

(5)

注意到利用反证法可以证明Ωi(t)∩Ωj(t)=∅,∀i≠j.事实上,假设该结论不成立,即存在x∈Ωi(t)∩Ωj(t),不妨设xi∈Ωi,xj∈Ωj,则有x=(1-t)xi+tyi=(1-t)xj+tyj,再由‖·‖的严格凸性可得:

‖xi-yj‖+‖xj-yi‖≤‖xi-x‖+‖x-yj‖+‖xj-x‖+‖x-yi‖=‖xi-(1-t)xi-tyi‖+

‖(1-t)xj+tyj-yj‖+‖xj-(1-t)xj-tyj‖+‖(1-t)xi+tyi-yi‖=‖xi-yi‖+‖xj-yj‖.

该式与‖x-y‖-循环单调性(见定义3及引理1)矛盾,从而结论得证.

以下我们给出传输密度的正则性结论.

(2)如果还有μ∈Lp,q(Ω)且p

由该不等式,Lorentz空间中Minkowski不等式(见定义6)以及式(5)可得

3 结论

针对以严格凸函数为费用函数时的最优计划所诱导的传输密度,本文给出了它的等价表达式,建立了其与位移内插的关系不等式,这一系列工作的目的是为了进一步证明该传输密度的绝对连续性与正则性. 这些结果将对与形状优化问题的Monge-Kantorovich方程的研究产生影响.