改进灰狼算法优化灰色预测模型在数控机床中的应用*

张英芝 朱继微 刘津彤 翟粉莉 牟黎明

(吉林大学机械与航空航天工程学院，吉林 长春 130025)

随着市场对制造业产品质量的高要求，数控机床呈现出高精度、长寿命的发展趋势，通过可靠性试验获取机床故障数据时间成本与费用成本日趋增大[1-2]。并且为保证数控机床的高可靠性加工需求，对故障的精准预测是切实需要的。所以如何在小样本数据情况下对机床故障进行高精度预测，即建立同时达到“小样本”与“高精度”要求的预测模型，是制定预防维修策略中的重要一环。

王鑫等[3]建立LSTM预测模型，通过网格搜索方法优选模型参数，利用民航飞机故障数据验证了该方法的应用能够显著提升模型精度。李雪等[4]通过遗传算法对神经网络模型中参数进行优选，相比基础神经网络预测模型其精度更高。文献[3-4]中的预测模型都有良好的预测精度，但由于模型自身特点的限制，需要历史故障数据量较大。王强军等[5]利用轴承故障数据建立指数平滑模型对故障时间进行预测，并通过建立威布尔分布可靠性模型验证该模型的有效性。Zhou P[6]将灰色理论与三角残差修正技术相结合建立预测模型，在电力需求领域获得了良好的预测精度。徐文等[7]提出利用粒子群算法对传统灰色预测模型的背景值优化，构造出改进的灰色模型并用于数控机床故障预测。文献[5-7]均是在小样本的情况下进行故障预测，无需大量的历史数据，但是模型预测精度仍有上升空间。

故本文提出一种改进灰狼算法与灰色理论相结合的故障预测模型(改进GGWO)，对基本灰狼算法的算法参数进行改善，并用于优化灰色预测模型中的背景值，建立最优预测模型。并将其与灰色理论和基本灰狼算法相结合的模型(GGWO)、灰色理论和粒子群算法相结合的模型(GPSO)进行预测精度对比，验证所提预测模型的有效性。

1 GM(1,1,P)预测模型的建立

GM(1,1)模型建立原理是在原始数列累加得到新序列后，建立微分方程，将方程的解序列进行累减运算后获取预测值[8]。

GM(1,1,P)模型是以GM(1,1)模型为基础发展而来的，其具体建模过程如图1。

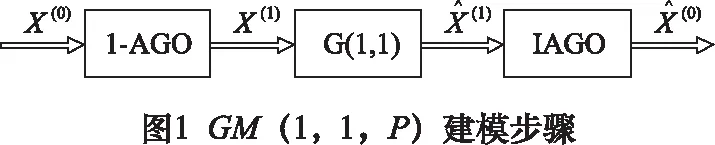
(1)累加数列的生成

对原始序列X(0)={x(0)(k),(k=1,2,…,n)}进行一次累加运算(1-AGO)得到X(1)={x(1)(k),(k=1,2,…,n)}，其中

(1)

其中：a、b为待定系数。

(2)建立灰色差分方程

确定序列X(1)的紧邻均值生成序列Z(1)={z(1)(k),k=2,3,…,n}，其中Z(1)满足式(2)：

z(1)(k)=p(k)x(1)(k-1)+[1-p(k)]x(1)(k)

(2)

其中：背景值p(k)∈[0,1]。

将X(1)序列离散化的变化规律对其进行离散化。可得到GM(1,1,P)的灰色差分方程：

x(0)(k)+az(1)(k)=b

其对应的一阶微分方程为：

(3)

其中：a、b为待定系数，t为时间。

(3)求解待定系数a、b

令：

(4)

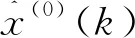
由最小二乘原理，有：

(5)

记：

则根据式(5)可得到：

A=(BTB)-1BTYN

(6)

根据式(6)可求得a、b的值。

(4)获得原始数列的预测值

将a、b的值代入式(3)，可得到：

(7)

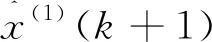
(8)

2 改进灰狼算法优化灰色预测模型

GM(1,1,P)模型中一般背景值定义为p={0.5}，即为传统GM(1，1)模型[9]。然而实际应用过程背景值P不同，对应的预测结果也不同[10]，所以需要对P值选优。本文设计一种改进的灰狼算法，对原灰狼算法的算法参数进行改善，用于优化灰色预测模型中的背景值，以获得最优预测模型。

2.1 基本灰狼算法(GWO)

GWO算法是模拟狼群狩猎活动的一种算法，核心思想是通过在狼群特有的社会等级制度下完成捕猎任务来完成寻优[12]。其中α狼总领灰狼群体，β狼层级低于α狼，δ狼层级低于β狼，三者对ω狼起领导作用。群狼逐渐向猎物逼近的距离和位置定义为：

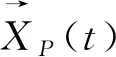
其中：tmax为最大迭代次数。

已知猎物位置后，狼群进行捕食活动， 利用α、β、δ狼判断猎物的位置，描述如下：

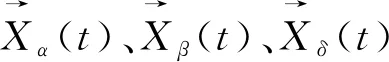
(9)

(10)

(11)

(12)

根据式(12)定义ω狼的最终位置。

2.2 灰狼算法的改进

由于基本灰狼优化算法的收敛因子m是线性迭代得到的，无法对全局与局部搜索能力进行平衡，且Chiu C Y[12]等证明线性收敛过程对重要参量的更新往往不是最优选择。故提出一种非线性收敛因子:

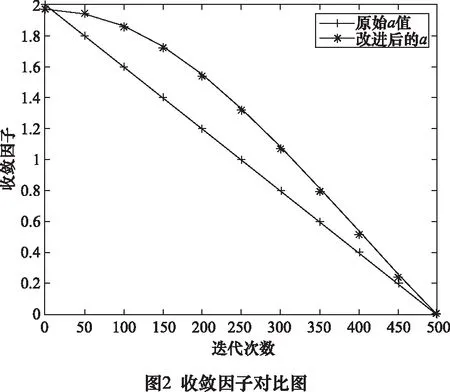
其中：μ为调节系数。收敛因子对比如图2所示。

根据图2可知，m值前期递减速度慢，狼群捕食步幅大，可发现较多潜在全局最优点；后期m值递减速度快，狼群捕食步幅小，提高了局部最优值的搜索能力。有效平衡了算法中局部与全局的搜索能力。

2.3 改进灰狼算法优化GM(1,1,P)预测模型

2.3.1 适应度函数

(13)

2.3.2 预测模型设计

应用灰狼算法优化初始预测模型的目标是求出适应度最好的一组灰狼位置，寻取灰狼最优位置即最优背景值建立最终的预测模型。模型框架如图3所示。

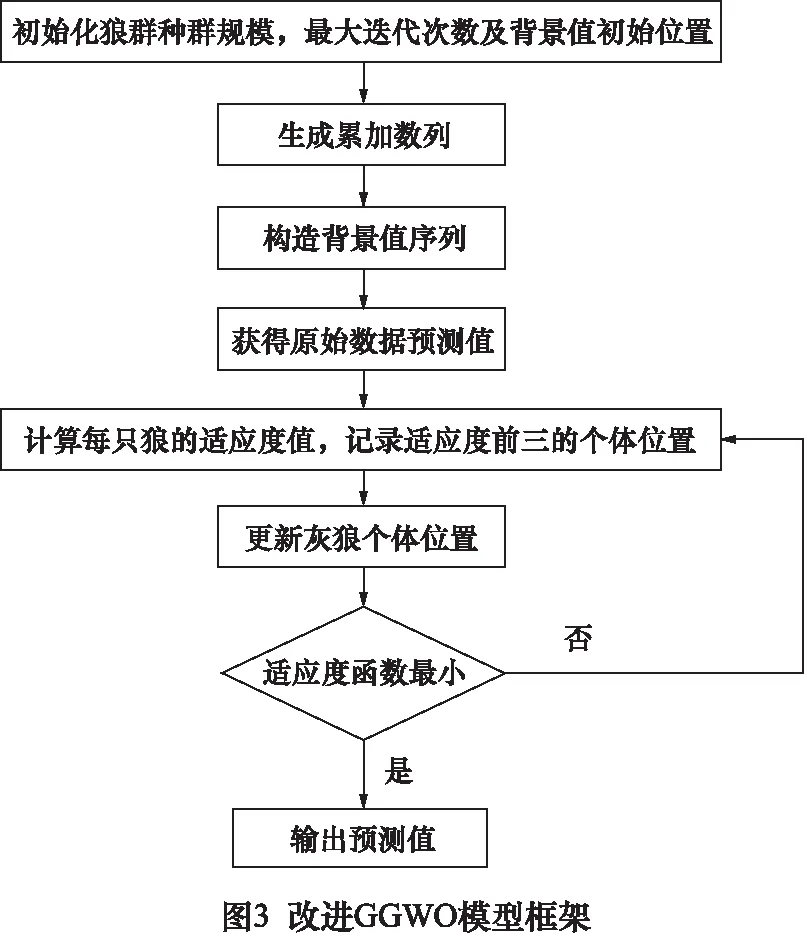
预测模型构建具体步骤如下：

(1)设置狼群种群规模N,最大迭代次数tmax及背景值的初始位置xi。

(2)将原始数列X(0)通过式(1)生成累加数列X(1)。

(3)根据公式(2)构造背景值序列Z(1)。并根据公式(6)获得待定系数a、b的值。

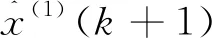
(6)根据公式(9)～(12)更新灰狼个体的位置。

(7)以适应度值最小为算法结束的判定条件，若符合要求输出预测值，否则，重复执行步骤(5)、(6)。

3 实例分析

以文献[7]中某型号数控车床主轴8个故障数据为原始数据，以平均绝对误差(MAE)与均方根误差(RMSE)为模型有效性的验证指标，将本文所提模型与GGWO模型、GPSO对比，验证该模型的有效性。

主轴具体故障数据如表1第2列所示，单位为h，将各算法初始参数设置如下：N=10,tmax=200,xi=0.5；设置GWO收敛因子的调节系数μ=2.5；设置PSO加速因子为1.5。不同模型预测值及相对误差值见表1，各模型与原始数据的拟合结果见图4，相对误差值见图5。

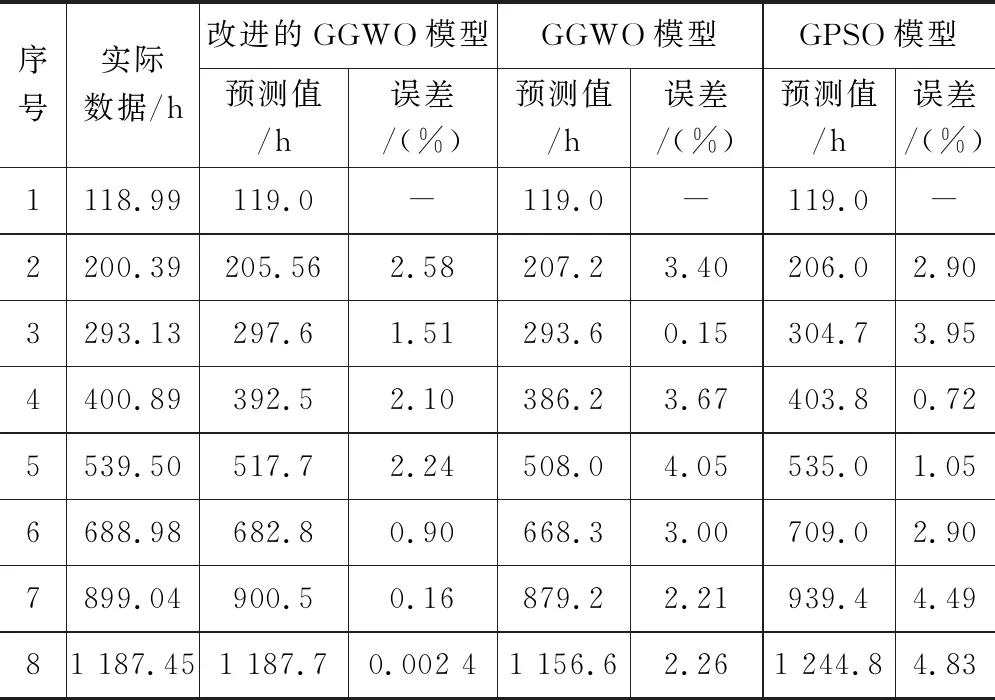
表1 不同模型预测值及相对误差

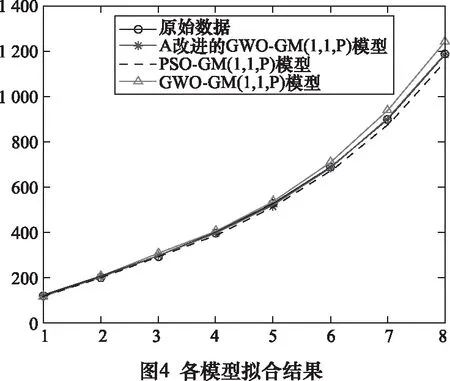
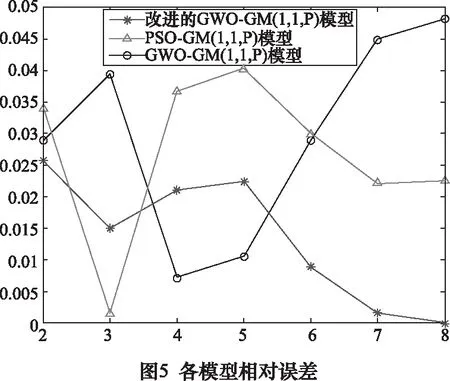
由图4可知，各模型输出的故障预测时间序列与原始故障时间序列的整体趋势是相同的，且改进GGWO模型与原始故障时间序列拟合度最高。由图5可知，改进的GGWO模型相对误差值波动幅度相比于其他模型最小，最大值为2.58%。

RMSE、MAE计算公式如式(14)、(15)：

(14)

(15)

各模型评价指标结果如表2。

表2 各模型评价指标计算结果

根据表2可知，本文所提模型的MAE与RMSE值均为最小，GGWO模型次之，GPSO模型计算值最大。综上，改进的GGWO模型相较于GGWO模型、GPSO模型，与原始故障时间序列拟合度最高，预测稳定性最好。

4 结语

(1)本文在基本灰狼算法基础上提出非线性收敛优化策略，有效改进了群体智能算法中全局与局部收敛不平衡及迭代速度较慢的问题。

(2)本文通过改进灰狼算法优化GM(1,1,P)中背景值，以建立更高精度的故障预测模型。解决了高预测精度与小样本、贫信息的矛盾，为类似预测模型构建提供指导。

(3)以平均绝对误差值、均方根误差值为模型评价指标，对比本文所提预测模型与其他预测模型，验证了该模型的有效性。