基于可学习权重衰减的大规模MIMO信号检测

武苗苗，傅友华

（1.南京邮电大学电子与光学工程学院、微电子学院，江苏 南京 210023 2.南京邮电大学射频集成与微组装技术国家地方联合工程实验室，江苏 南京 210023）

未来移动通信网络的发展旨在提高网络容量、频谱效率和降低延迟。大规模多输入多输出（Multiple⁃Input Multiple⁃Output，MIMO）技术是第五代移动通信系统的关键技术之一，其中蜂窝网络的基站配备了数十、数百或数千个天线［1］。然而，随着天线数的增加，传统的信号检测算法的性能和复杂度难以满足下一代通信系统的需求。

传统的MIMO信号检测方案大致可以分为两类：线性检测算法和非线性检测算法。最大似然（Maximum Likelihood，ML）［2］检测器的检测性能虽是最优的，但其复杂性令人望而却步。线性检测算法，如迫零检测（Zero Forcing，ZF）［3］算法和最小均方误差（Minimum Mean Square Error，MMSE）［4］算法，虽具有较低的复杂度，但它们的误码率较高。随着MIMO系统天线数的增加，系统对检测性能要求越来越高，线性检测算法的检测性能已经无法满足。为了提高检测算法的性能，通信领域学者将研究重心转向了非线性检测算法的研究。例如，球形解码器（Sphere Decoder，SD），虽然提供了接近最优的性能，但其复杂性仍然随着天线数目的增加呈指数增长［5］。基于优化的检测器，如：半正定松弛（Semi⁃Definite Relaxation，SDR）［6］和近似消息传递（Approximate Message Passing，AMP）［7］，虽在某些情况下可实现接近最优的性能，但前者的代价是高次多项式复杂度，后者的代价是迭代特性导致的发散。总之，大多数现有技术过于复杂，无法实现下一代大规模MIMO系统所需的规模。深度学习作为一种普适性算法，已经在许多领域带来了前所未有的性能提升，例如机器人、电子商务、计算机视觉和自然语言处理等领域。在大规模MIMO系统中使用深度学习，这将会是一个很好的研究方向。

在深度学习中，最近的发展提出了“learning to learn”的方法。该方法将一个迭代算法展开到固定的迭代次数，每次迭代被认为是一个层，展开的结构称为深度神经网络（Deep Neural Networks，DNN）。这种模型驱动的深度学习方法可以达到或超过相应的迭代算法的性能［8］。胡钟秀等［9］将简化近似消息传递迭代（Simplified Approximate Messaging Passing，SAMP）检测算法与深度学习结合，提出了新型模型驱动的深度学习网络SAMP⁃Net，通过学习得到最优可训练的参数，提高检测性能。Samuel等［10］提出的检测神经网络（Detection Network，DetNet）算法是深度展开技术在MIMO检测中的成功应用之一，它由投影梯度下降算法展开。Ma等［11］在传统正交近似消息传递（Orthogonal Approximate Message Passing，OAMP）算法的基础上，结合深度神经网络构建了 OAMPNet［12］网络模型，该模型在小尺度相关信道上有良好的性能。DetNet和 OAMPNet都是离线训练的。Khani等［13］提出了大规模MIMO独立同分布模型（Massive MIMO⁃independent identically distributed，MMNet⁃iid），该神经网络是在AMP的基础上迭代展开，并添加了可训练参数，在独立同分布高斯信道上有良好的性能。

一般来说，通过设计更深层次的神经网络架构来解决信号检测问题，这会显著增加训练时长和计算复杂度，但并不会显著提高检测性能。因此就迫切需要设计具有可扩展性的DNN架构，使得该架构可以加速训练的同时提高检测性能。正是在这样的背景下，DNN在训练和推理方面的加速成为深度学习领域一个活跃的研究领域。最近降低复杂度的方法有 Drop⁃Connect［14］，Pruning［15］和 Dropout［16］。然而，这些方法中的大多数都是用来防止过拟合的，并没有被明确设计用来降低复杂度，提高性能。Dropout主要思想是在训练过程中随机舍去一些神经元，但这样无法保证目标函数单调性。虽然在计算机视觉中已经提出了许多关于DNN加速训练和推理的方法，但很少有针对物理层通信设计系统的DNN加速。Mcdanel等［17］通过向卷积神经网络（Convolutional Neural Network，CNN）的各层引入单调的非递增信道系数动态调整输入通道的数量，从而降低功耗和降低延迟，基于此本文试图通过提出一个可扩展的DNN模型来填补这一空白，以获得高效的大规模MIMO检测。

本文在MMNet⁃iid的基础上提出了新的基于权重衰减的网络架构（Weight Decay Network，WDNet），该网络架构基于投影梯度下降算法展开，并引入了单调非递增函数的概念。该函数缩放神经网络的每一层，且单调非递增函数本身是可训练的，从而允许网络在训练期间动态地学习其自身权重的最佳衰减策略。将单调非递增函数设置为可训练参数，提高了WDNet的检测性能。

1 系统模型

一个典型的多用户MIMO系统模型如图1所示。基站配备有Nr根天线同时服务于Nt个具有单天线的用户。

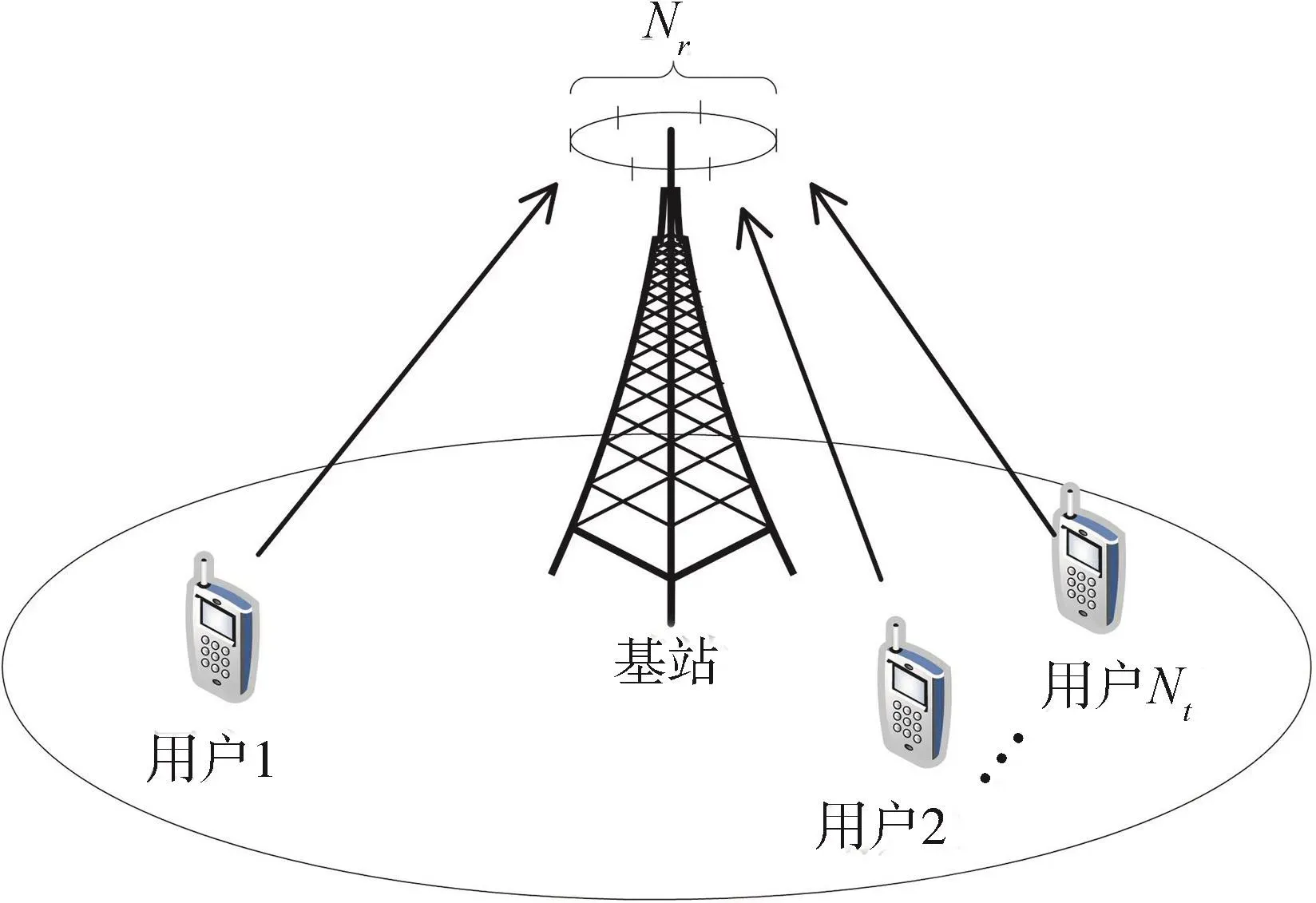
图1 一个基站配备Nr根天线和Nt个单天线用户的上行链路MIMO系统

为了能够应用于深度学习模型，将式（1）变换为实域

信号检测的目的是根据接收到的向量y＝Hx+n推断发送信号向量x，其中，H为信道矩阵，n为高斯噪声。在MIMO信号检测中，假设信道状态信息已知。在ML中，对所有可用的传输信号组合进行比较，并计算似然检验，其表达式为

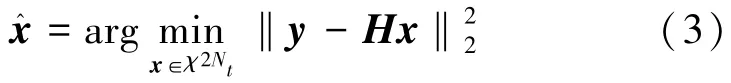
ML检测通过寻找最小距离度量来选择最终的信号组合。ML检测理论上是恢复传输信号的最优方法，但其计算复杂度随着天线数的增多而呈指数增加，因此不适用于大规模MIMO系统。在下一节中，将使用深度学习方法解决这一问题。

2 基于可学习权重衰减的大规模MIMO检测

WDNet是一种非线性估计器，通过投影梯度下降优化的递归公式展开ML度量来设计。本文提出的检测器将单调非递增函数应用于现有的检测网络。这种修改降低了训练检测器的复杂度且提高了检测性能。

2.1 单调非递增函数β

不完全点积（Incomplete Dot Products，IDP）在正向传播的点积计算中增加了一个由单调非递增函数β组成的剖面。这使得系统以最高到最低递减的方式优先选择层权重。数学上，对于两个给定的向量x＝［x1，x2，…，xN］T和y＝［y1，y2，…，yN］T，其 IDP的截断形式［19］为

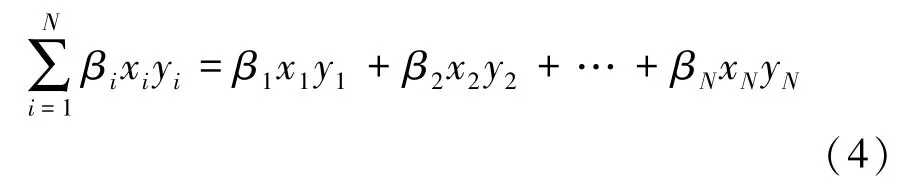
式中，β1，β2，…，βN为单调非递增函数系数。

在标准全连接网络中，前馈传递输出为

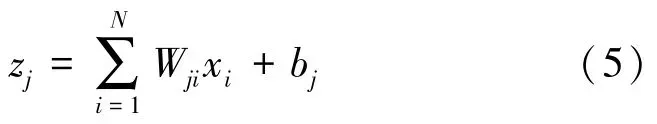
式中，j∈｛1，…，M｝，M为输出分量的个数，N为输入分量的个数，i，j分别为输入、输出维数；xi为第i个输入分量，Wji为第j个输出分量和第i个输入分量对应的信道或层权重，bj为偏倚。对不完全线性层进行如下计算

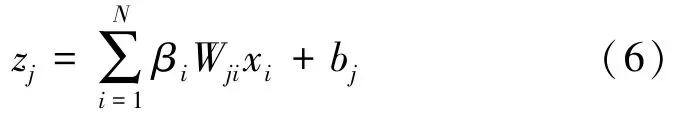
本文为权重引入单调非递增函数［17］，表达式为

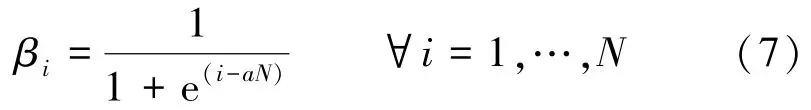
式中N为发送天线数，由图2可知单调非递增函数β的阈值与a（0≤a≤1）有关，因此不同a所对应的单调非递增函数对WDNet性能的影响将在第3节给出，并通过仿真找到a的最佳值。从图2可以看出，该函数后半部分为衰减函数，通过衰减函数衰减了一半的通道系数。这意味着它允许网络训练调整梯度流，使重要的权重保存在未衰减的一半中，而不太重要的权重保存在衰减的一半中。

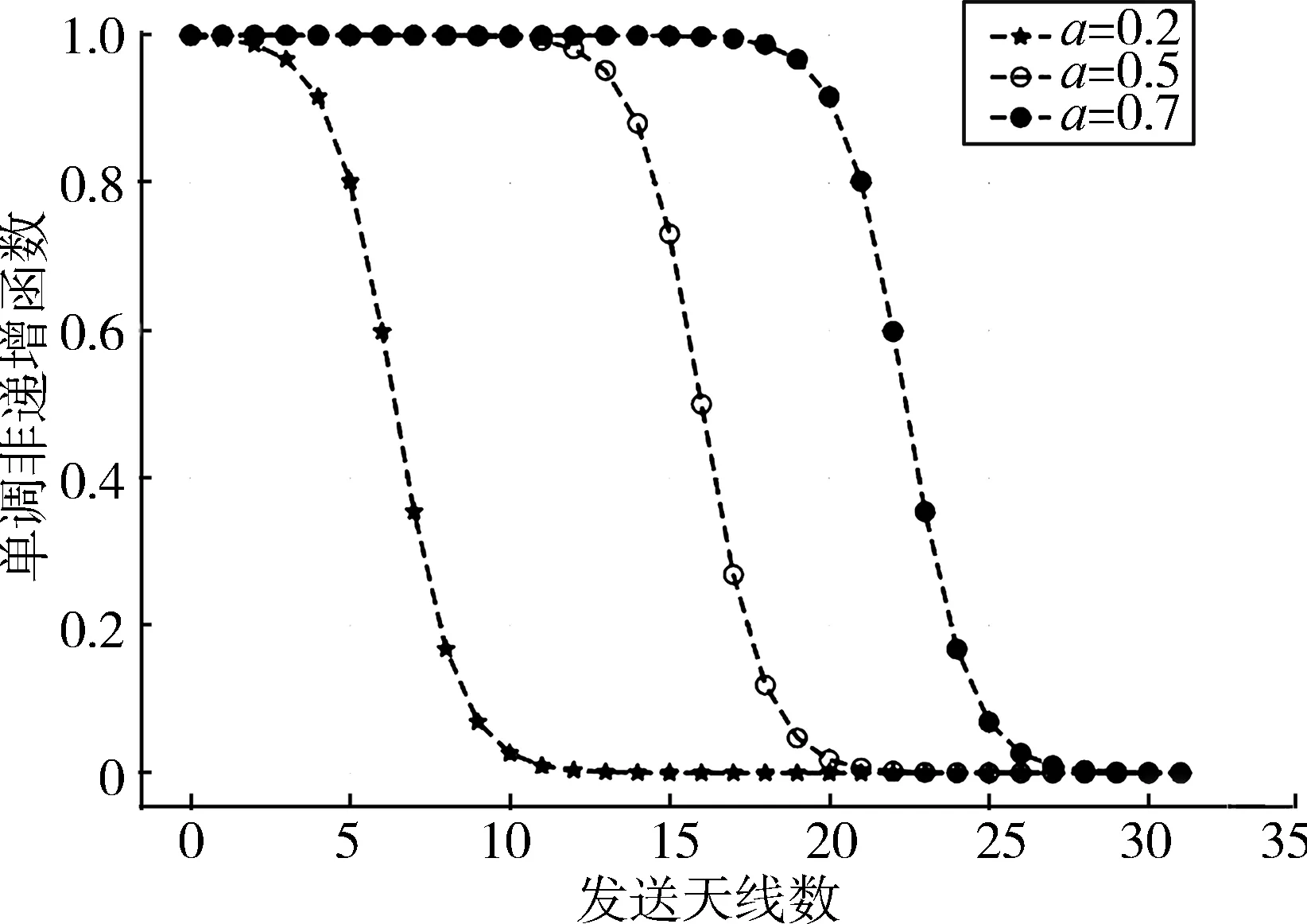
图2 单调非递增函数VS发送天线数

为了进一步提高WDNet的性能且在训练期间动态地对权重进行优先级排序，将单调非递增函数设置为可训练参数。在训练和梯度更新过程中，单调性是通过式（7）函数的形状来维持的。在训练过程中，对每一个权重进行不同的缩放，当训练次数达到一定时，每一个权重的单调非递增系数都达到一个最优值，从而提高WDNet的检测性能。由于权重的饱和，a达到一定值后单调非递增函数对WDNet性能的影响将趋于平稳状态。当a较小时，由于大部分权重被衰减，使得网络的前馈推理不完整，从而会降低算法的收敛性和检测性能；当a较大时，由于保留了大部分权重，增加了算法的复杂度。因此寻找一个合适的a以达到准确性和复杂度的平衡是必要的。

2.2 WDNet算法

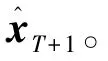
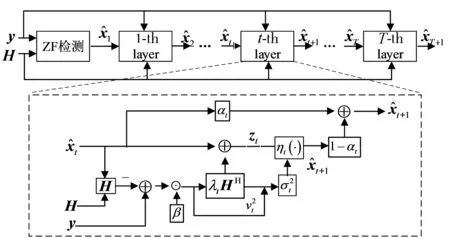
图3 WDNet结构框图

该神经网络第t层（1≤t≤T）的计算过程如下

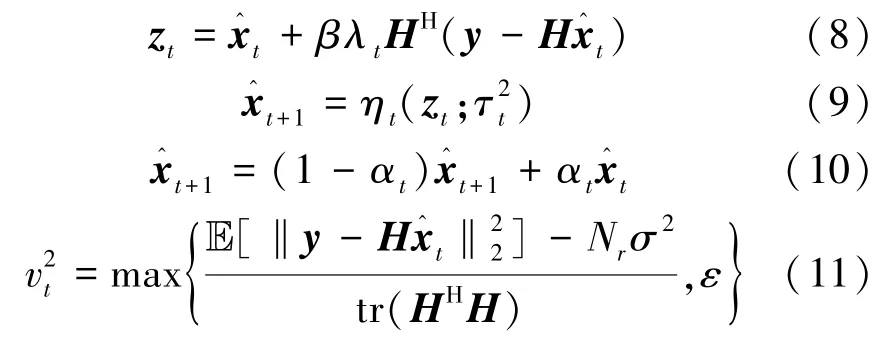
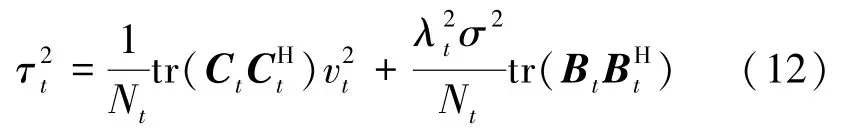
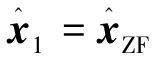
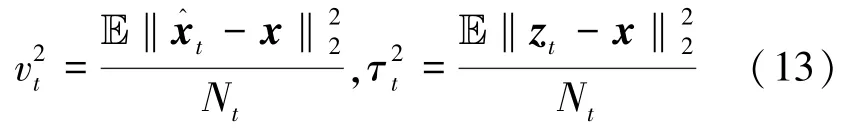
太宰治：我的不幸，恰恰在于我缺乏拒绝的能力。我害怕一旦拒绝别人，便会在彼此心里留下永远无法愈合的裂痕。

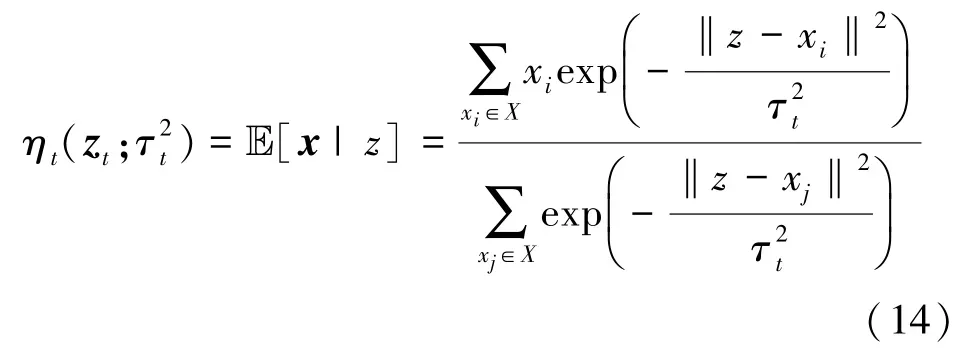
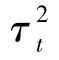
为了进一步提高WDNet的检测性能，引入式（10）所示 ResNet的残差特性［22］。

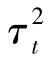
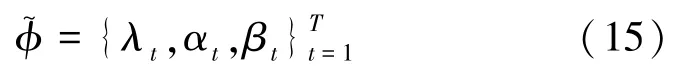
WDNet连接了上述形式的T层。其损失函数为所有T层的平均L2损耗

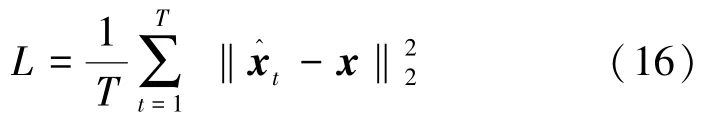
3 仿真分析

本节通过仿真评估和比较WDNet与其他检测方案在独立同分布高斯信道的性能。首先描述仿真要素；然后分析单调非递增函数对WDNet性能的影响，WDNet的复杂度、收敛性、误码率性能，以及对MIMO配置和调制的鲁棒性。

3.1 仿真要素

（1）数据：训练和测试数据通过式（1）中所描述的模型生成，发送信号x经过QAM16调制产生。瑞利衰落信道矩阵H从i.i.d高斯分布中采样（即，H的每个元素是复数正态分布：H∈ CN（0，（1/Nr）INr））。系统的信噪比（Signal Noise Ratio，SNR）定义为

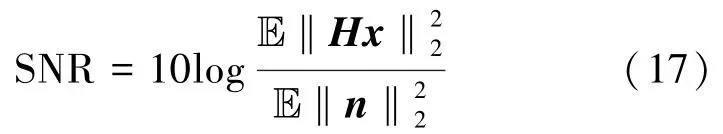
表1 训练网络所需参数及取值

3.2 性能分析

（1）单调非递增函数对WDNet性能的影响：图4展示了在13 dB和15 dB信噪比下不同a所对应的单调非递增函数对WDNet性能的影响。从中可以看出，13 dB和15 dB信噪比的误码率性能随着a的增加而提高，但由于权重饱和，误码率在a＝0.5时饱和，并且此时WDNet准确性最高。因此在之后的训练中，将a设置为0.5。

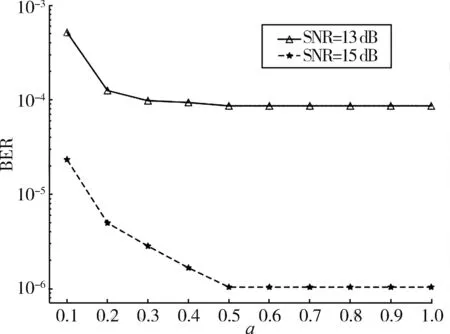
图4 不同a所对应的单调非递增函数对WDNet误码率性能的影响

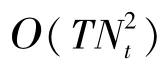
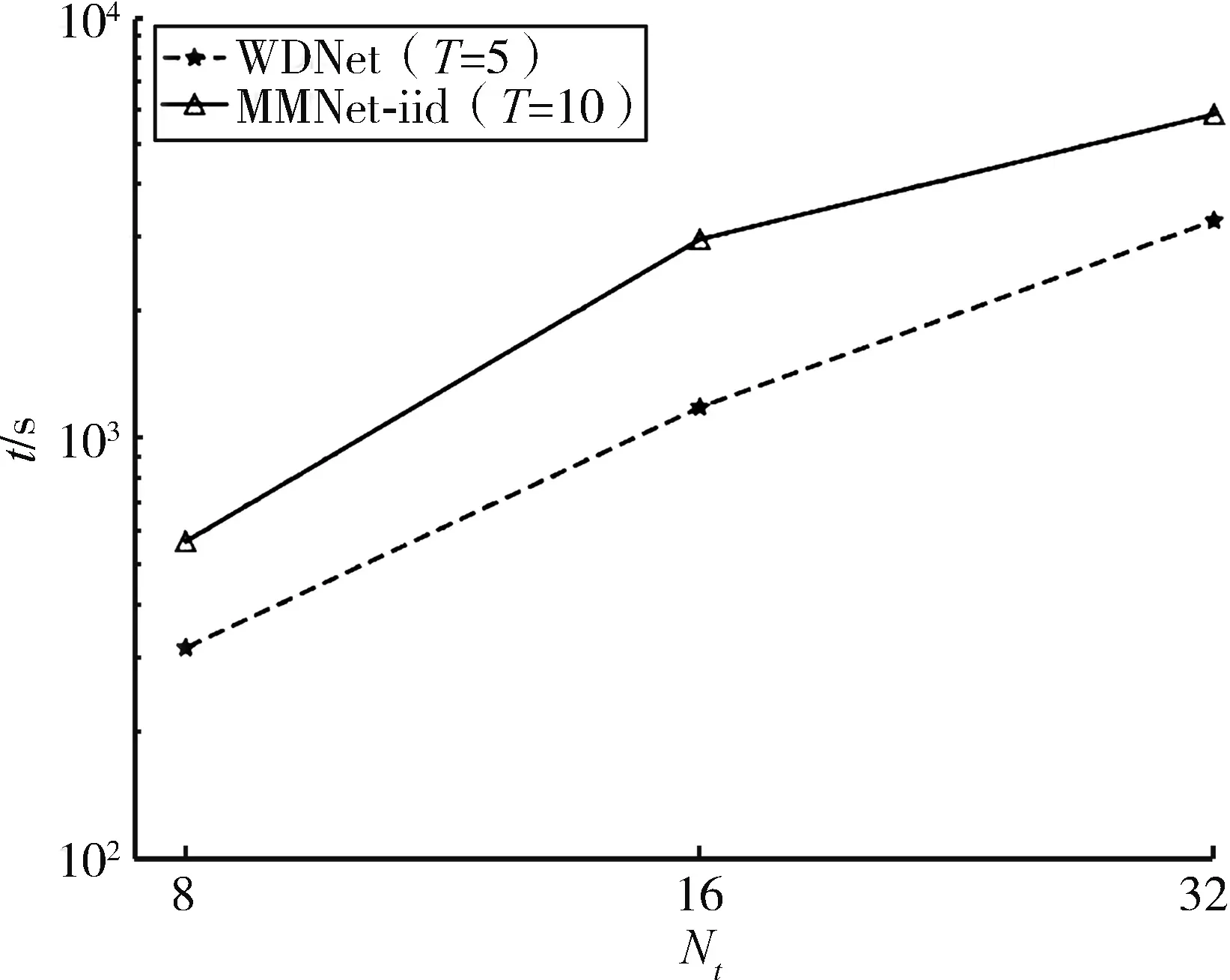
图5 WDNet和MMNet⁃iid的CPU运行时间与天线数的关系

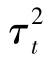
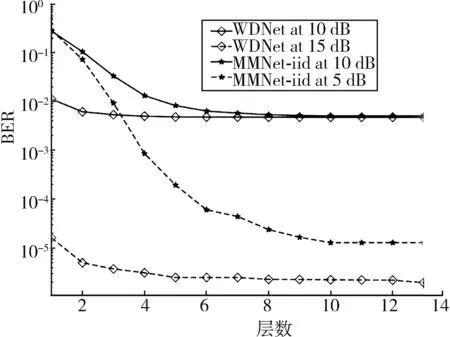
图6 WDNet，MMNet⁃iid的误码率（BER）性能和层数的关系

（4）性能比较：图7展示了当天线配置为16×64且调制方式为QAM16时，神经网络算法WDNet、MMNet⁃iid、DetNet 及传统检测算法 AMP、SDR、MMSE的误码率性能。由图7可知，所有方法的准确性都随着信噪比的增加而增强。从图中可以看出，AMP在较高的信噪比情况下会遇到鲁棒性问题。WDNet检测方案在所有设置下都比传统检测方案MMSE，AMP和SDR拥有更好的准确性。这表明深度学习在解决通信问题上具有优越性。DetNet在高阶调制下，准确性低于MMSE。同时本文提出的 WDNet误码率性能优于 MMNet⁃iid 和 DetNet，并且信噪比越高准确性越好。误码率为10-5时，WDNet的性能与 MMNet⁃iid性能之间具有约1 dB的性能增益。

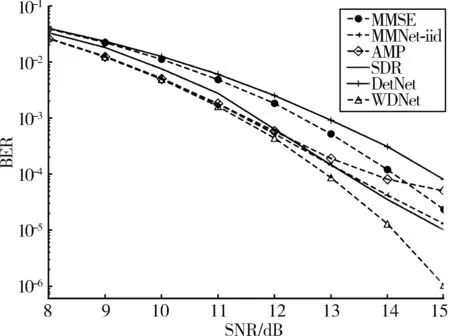
图7 WDNet与其他检测器误码率性能的比较

（5）对MIMO配置和调制的鲁棒性：由于可用于在线训练的数据和计算资源有限，验证离线训练网络的鲁棒性尤为重要。图8展示了MIMO配置和调制不匹配时 WDNet的误码率性能。在 16×64MIMO系统中，用QAM16调制符号训练WDNet，并测试训练参数的鲁棒性。

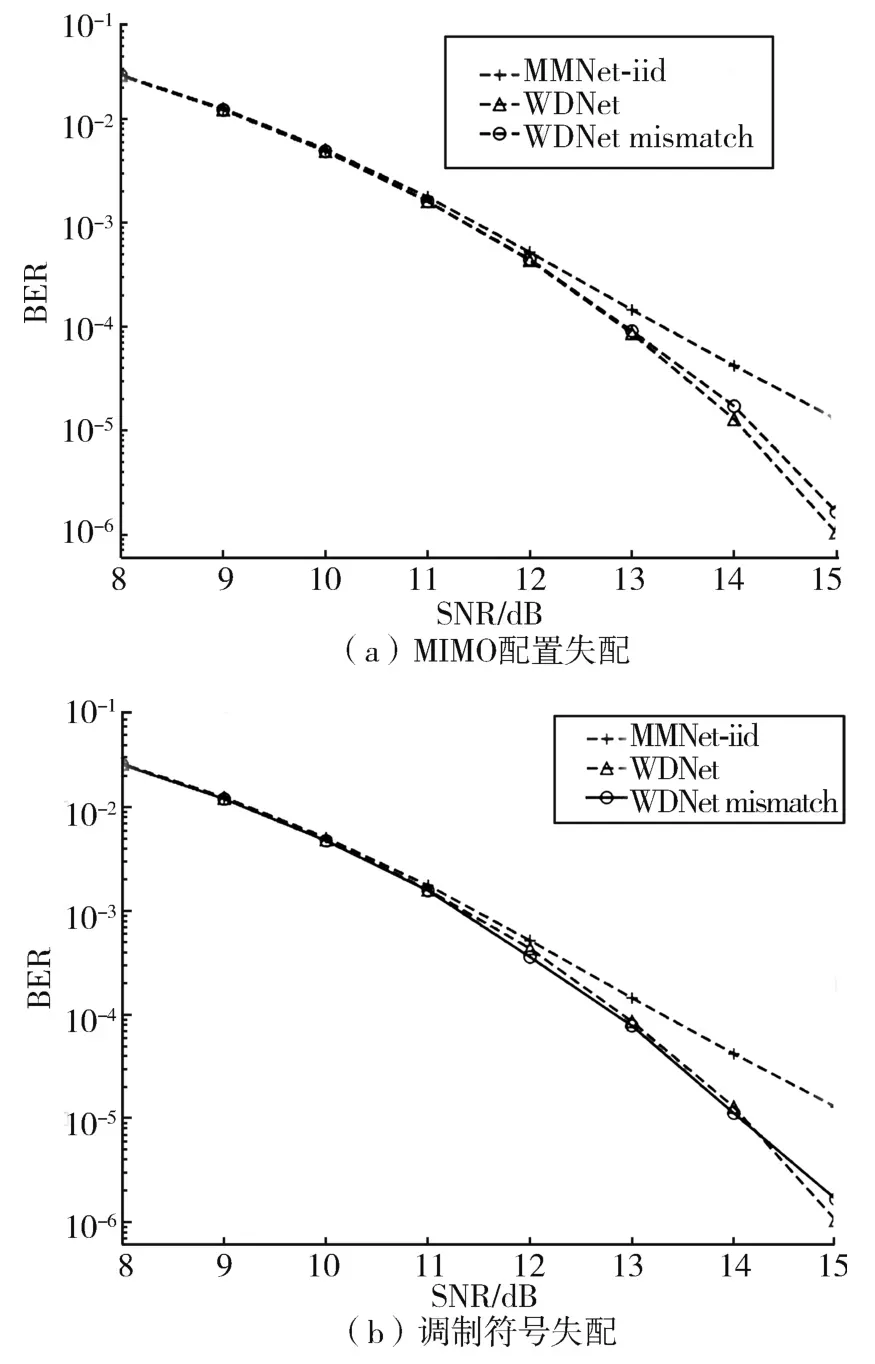
图8 WDNet与 MMNet⁃iid在 MIMO 配置失配和调制符号失配情况下性能比较

图8（a）展示了在 MIMO配置不匹配情况下WDNet的误码率，其中网络在具有QAM16的8×32系统中进行测试。虽然训练和测试采用了不同的配置，但WDNet性能仍然优于MMNet⁃iid，且性能损失很小。这种鲁棒性表明WDNet对不同的MIMO配置具有灵活性。此外，图8（b）显示了调制符号不匹配情况下WDNet的性能，其中网络在16×64系统中使用BPSK调制方式进行测试。当BER＝10-4时，WDNet仅因调制符号失配造成0.2 dB的性能损失，这表明WDNet对调制符号失配具有鲁棒性。因此，可以在具有不同调制符号的不同MIMO配置中直接使用已训练的网络。

4 结束语

本文对基于深度学习的大规模MIMO信号检测进行了研究。在MMNet⁃iid的基础上提出了WDNet算法。该算法使用单调非递增函数在训练期间动态地对层权重进行优先级排序。为了提高WDNet对激活函数变化的鲁棒性，允许单调非递增函数本身在所提出的体系结构中是可训练的参数，这提高了检测精度。从仿真结果可以看出，具有可训练参数的WDNet检测性能优于MMNet⁃iid检测性能，并且对各种失配具有优越的鲁棒性。

附录

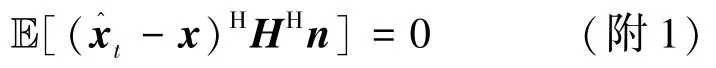
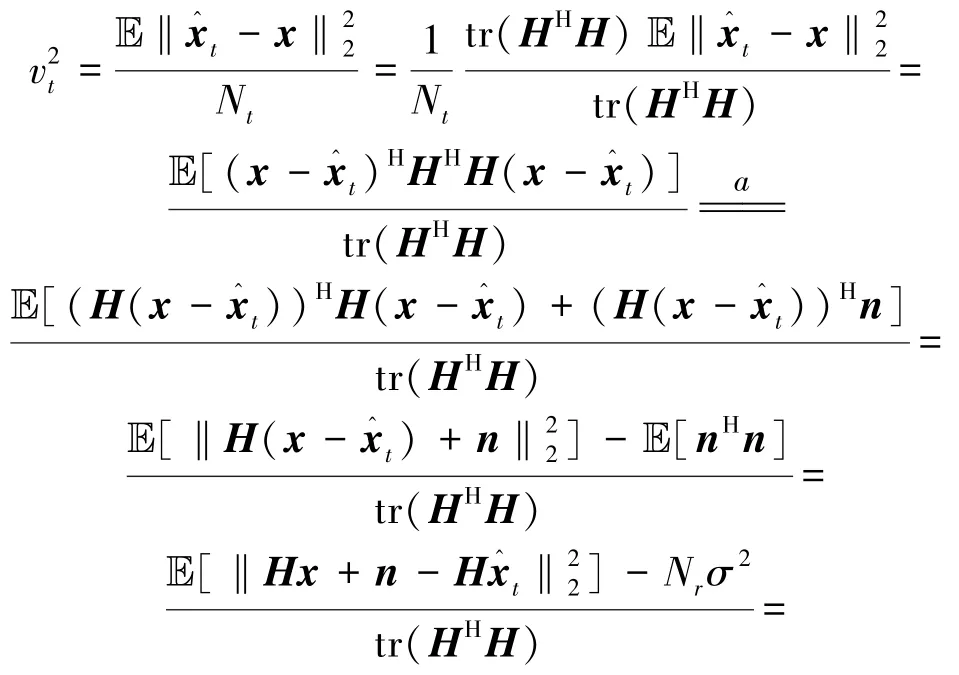
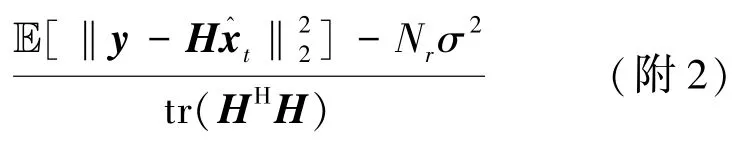
假设2：zt-x由独立于x的i.i.d零均值高斯项组成。

首先误差向量zt-x可以重写为

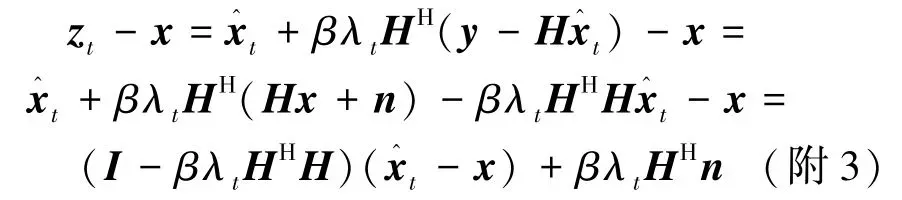
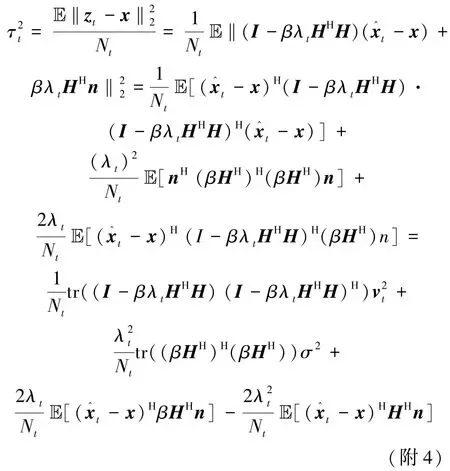
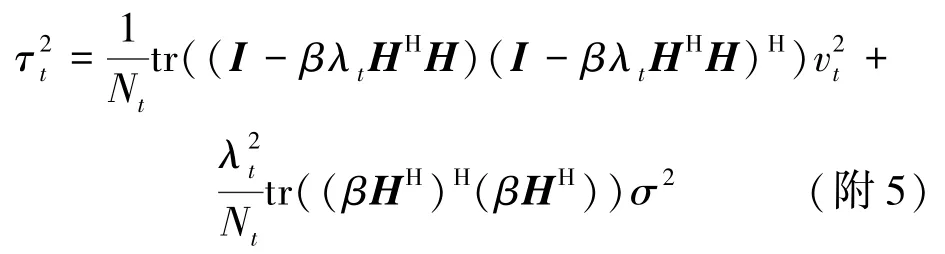
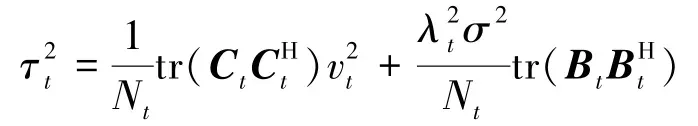
其中，矩阵 Ct＝I-βλtHHH，Bt＝βHH。