多径信道下FTN技术的性能分析

韩双锋，夏 亮，王启星，王江舟

（1.中国移动研究院，北京 100053 2.肯特大学工学院，英国 坎特伯雷 CT2 7NT）

按照无线通信系统十年一代的发展规律，2030年将部署6G网络，以满足不断飞速增长的无线通信业务需求。预计6G阶段的业务需求比5G阶段会有大幅度的提升，例如200 Gbit/s的下行峰值速率，用户面时延小于0.1 ms，支持1 000 km/h的移动速度，至少50%以上的频谱效率提升，以及100倍的能量效率提升等［1］。为了满足如此高的业务需求，业界在6G关键技术方面开展了广泛研究，力求在物理层和网络架构等方面取得实质突破［2-5］。尤其是高能效的绿色通信技术［5］，对6G和未来通信系统的可持续发展至关重要。

在传统通信系统中，为了避免符号间干扰，通常采用奈奎斯特准则，确保在不同时刻的发送脉冲在采样点处满足正交性。超奈奎斯特技术（Faster than Nyquist，FTN）［6-9］早在 20 世纪 70 年代就被提出，后来又扩展到频域，例如 SEFDM（Spectrally Efficient Frequency Division Multiplex）技术［10-11］。这些超奈奎斯特技术的特点，是将待发送的基带数据符号以大于奈奎斯特采样的速率，在时域或者频域与脉冲成型函数进行卷积后得到待发送信号。每个符号经过成型滤波器后被调制到一个波形，FTN处理后，N个连续符号被调制到N个时域或者频域波形，波形之间的时域或者频域间隔是传统奈奎斯特系统的1/K。Anderson等［6］推导了FTN技术的容量界，发现其高于基于奈奎斯特准则的信号方式，并将这一结果归因于使用了非Sinc成形滤波器（如根升余弦滤波器）使用的多余带宽。不同于传统的正交传输，超奈奎斯特采样技术利用发送端的非正交信号设计结合接收端过采样处理，有望提升通信系统容量和频谱效率，是6G潜在关键技术方向之一。

超奈奎斯特技术通过发送端传输更高速率的非正交信号，在传输时不可避免地引入符号间干扰，因此处理系统中的符号间干扰是一个重要研究课题。近年来业界提出了诸多的解决方案，一个经典的思路是通过发送端预编码以及接收端的联合处理。文献［9］推导了预编码FTN技术的容量，还给出了最优的功率分配策略，结论表明其方案的频谱效率超越了香农极限，然而此结果存在很大争议。文献［12］提出了基于预编码FTN的非正交多址技术，并和多天线技术进行了结合。

由于FTN技术自身的波形非正交特点，其在多径环境下的性能备受业界关注。文献［13］推导了预编码FTN技术在多载波系统中的容量，还给出了最优的功率分配策略。文献［14］研究了FTN技术在多径信道下的可达速率，并提出了一种干扰消除方案，以提升在多径信道的容量。

由于在时域多径信道下，FTN技术中既存在波形之间的干扰，还存在多径带来的严重的多径干扰，这给相关的科研工作带来很大挑战，业界对于FTN技术在多径信道下的容量研究还很不充分。本文研究了FTN技术在时域多径信道下的性能，推导了多径信道下的符号间干扰矩阵，并推导了系统的容量和频谱效率；进而通过数值仿真，验证了在不同信道环境下系统容量的变化规律；此外，还探讨了未来的一些研究方向。

1 系统建模

假设作用于时域符号的成型滤波器函数为f（t），考虑等间隔符号的情况（其他不等间隔的情况可以同理推导，不再赘述），相邻时域符号间隔为T，当过采样因子为K时，符号间隔T是奈奎斯特采样间隔的 1/K。考虑连续 N个数据符号，s＝［s0，…，sN-1］T，FTN 发送信号可以表示为

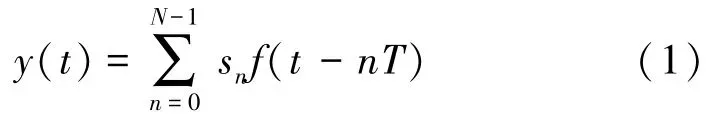
经过匹配滤波器f∗（-t）后，等效的总体滤波函数g（t）是f（t）与 f∗（-t）的卷积：

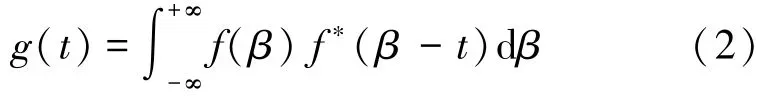
假设接收端噪声n（t）是均值为0、方差为σ2的加性高斯白色噪声（AWGN）。经过匹配滤波器后，噪声变为

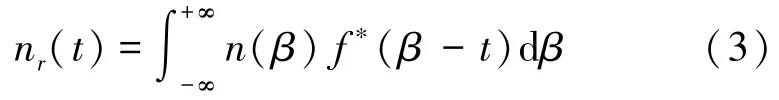
当考虑L径多径信道，相邻径之间的时延也为T，第l径的信道系数为hl，N个符号的接收信号可以表示为

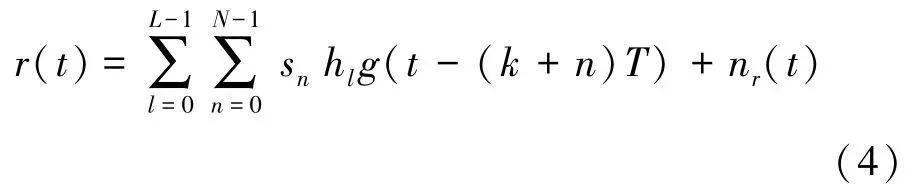
考虑每隔T时间的采样，信号的输入输出关系表示成如下矩阵形式

其中，r为接收端采样序列，Gc为考虑多径效果后的符号间干扰矩阵，nr为采样点噪声向量。

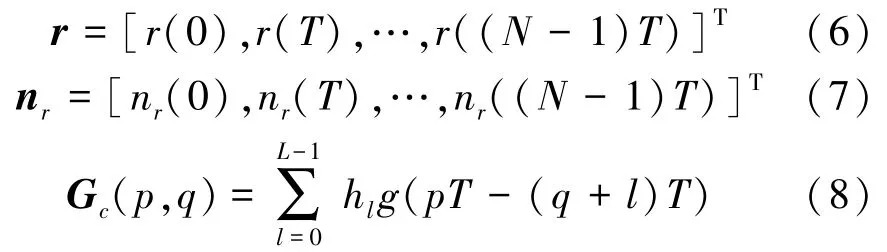
基于式（2）得到的AWGN信道下数据符号间的干扰矩阵G是一个拓普利兹矩阵，第一行为［g（0），g（-T），…，g（-（N-1）T）］。在多径信道下，接收端看到的符号间干扰矩阵Gc是由矩阵G的元素和多径信道的响应共同决定的。当L＝1，h1＝1时，Gc和G等效。

由于噪声不受多径影响，因此噪声向量的协方差矩阵为

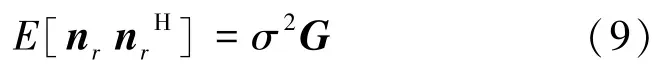
2 FTN容量分析

为了获得信道的容量（单位为bit/s）表达式，首先分析接收数据符号向量r和发送符号序列s之间的互信息，然后用这个互信息除以发送N个波形所需要的时间。首先，r和s之间的互信息表示如下

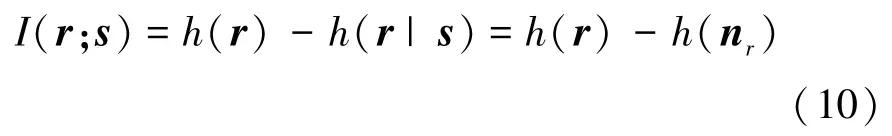
其中，h（r） 是向量 r的熵，h（nr） 是向量nr的熵。根据通信经典理论，h（r）和h（nr）可以分别写成如下的形式：

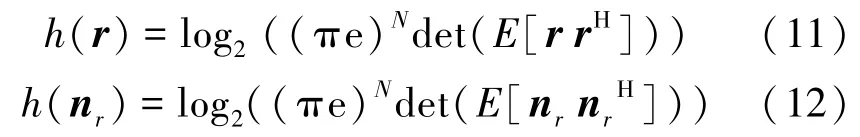
向量r的协方差矩阵可以表示为

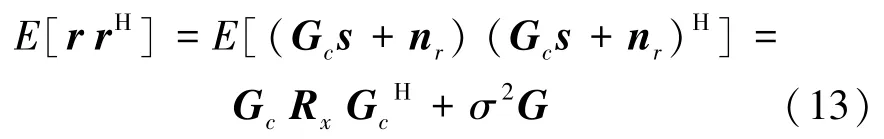
其中，Rx＝E［s sH］，是向量s的协方差矩阵。根据式（11）至（13），可以得到互信息 I（r；s） 的表达式：

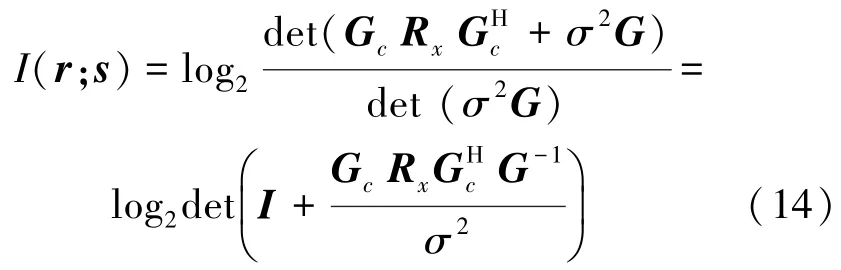
可以看出，互信息I（r；s）取决于发送和接收滤波器共同决定的矩阵G，向量s的协方差矩阵Rx，以及滤波器和信道信息共同决定的矩阵Gc。不同的多径功率分布和时延分布会产生不同的矩阵Gc，从而影响互信息。对发送符号的不同的功率分配会影响Rx，进而也会影响互信息。

考虑不同符号等功率分配的情况，假定奈奎斯特系统的发送功率为P，为了保证FTN系统的功率相同，每个发送符号满足均值为0、方差为P/K的高斯分布，显然 Rx＝E［s sH］＝（P/K）I。互信息I（r；s） 可以表示为

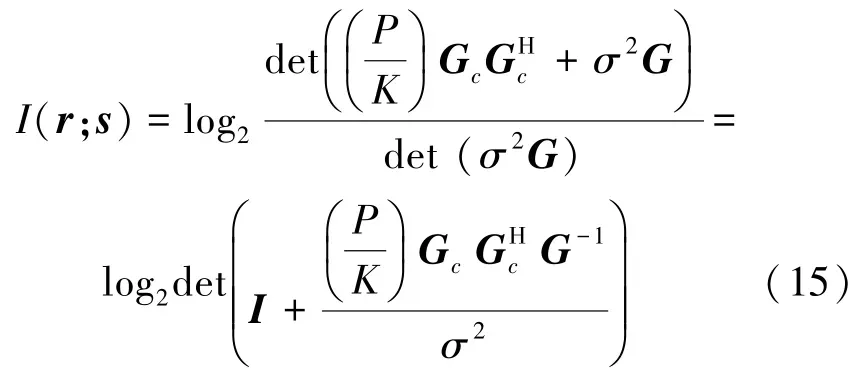
如果信道为平衰落，G＝Gc。互信息为

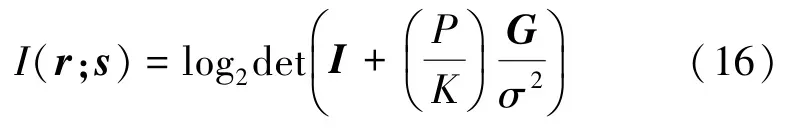
式（16）和经典信息论的结论是一致的，也就是说，FTN的容量取决于发送和接收滤波器的特性。然而，由于实际系统中多径衰落是普遍存在的，式（16）中的经典香农公式不能准确描述系统的性能，必须要基于式（14）结合具体的多径分布和功率分配情况（对应不同的Rx）来分析FTN系统的性能优劣。

得到互信息 I（r；s） 的表达式（15）后，等功率分配FTN系统的速率表示为

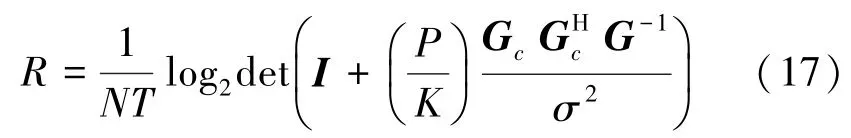
当N趋于无穷大时，即得到系统的容量C：

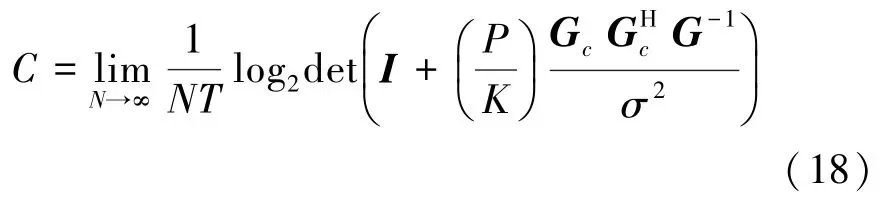
对于严格带限［-W，W］的系统，每秒发送的FTN符号数为2WK个，系统的容量可以表示为

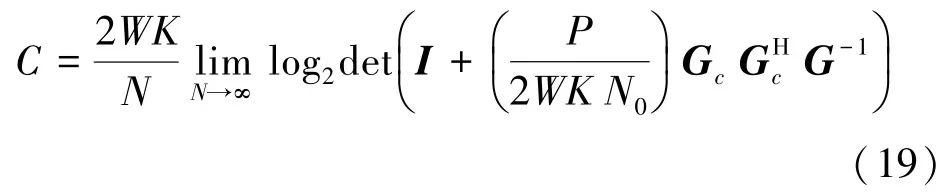
其中，N0为噪声的功率谱密度。系统的频谱效率SE（Spectrum Efficiency）表示为

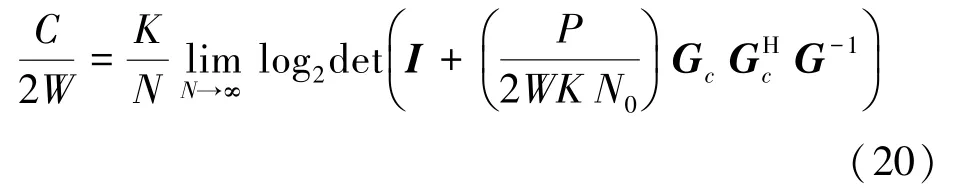
3 仿真结果与分析

3.1 不同符号间隔对频谱效率的影响

首先验证AWGN信道下FTN系统不同的符号间隔对系统频谱效率的影响。考虑理想时域Sinc函数作为脉冲成型函数，在仿真中截取1 000个正常符号间隔（考虑的时间范围为-500 KT～500 KT），信噪比SNR＝P/σ2。如图1所示，当FTN符号间隔变化时，例如K从2变化到5时，系统的频谱效率和AWGN信道下的香农频谱效率相同。也就是说，FTN技术通过发送端更密的波形进行数据传输，并没有超越传统香农的信道容量界。

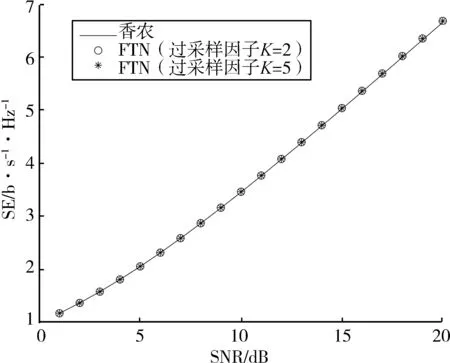
图1 AWGN信道下FTN系统的频谱效率

3.2 不同多径环境对频谱效率的影响

考虑理想的时域Sinc函数作为脉冲成型函数，在仿真中截取1 000个正常符号间隔（-500 KT～500 KT）。考虑4种多径信道，信道1是单径信道，信道2是3径信道，信道3是20径信道，信道4是30径信道。多径信道中的每条径服从瑞利分布且功率相同，每种信道中多径总功率保持一致。过采样因子K为5，相邻多径时延为T。

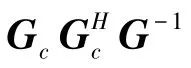
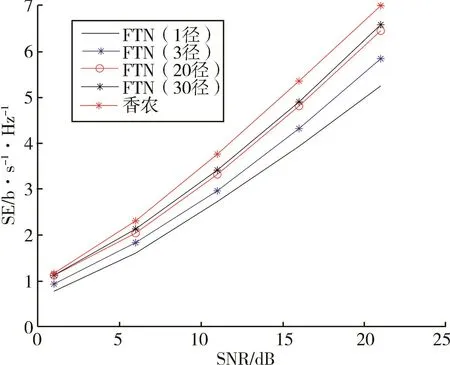
图2 多径信道下FTN系统的频谱效率

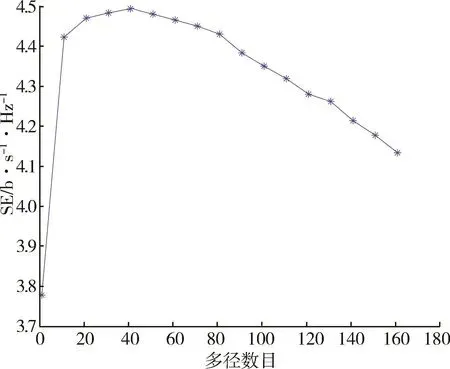
图3 FTN系统的频谱效率随多径数的变化趋势

4 结束语

FTN技术是未来6G通信系统的潜在关键技术。本文研究了FTN技术在时域多径信道下的性能，推导了多径信道下的符号间干扰矩阵以及系统的容量和频谱效率，并通过数值仿真验证了不同信道环境下系统频谱效率的变化规律。随着符号间隔的变化，FTN的频谱效率并不发生变化。在多径信道中，随着多径数目的增加，FTN频谱效率也相应地增加，在达到最大值后反而随着多径数目的增加而下降。

为了公式推导和仿真分析的简洁，本文的仿真分析假定不同符号进行等功率分配。当采用不同的功率分配时，Rx的取值会发生变化，从而影响系统的互信息。给定符号个数、多径分布、发送和接收滤波器的参数后，最优的功率分配策略也就被确定下来。但是求解使得容量最大的功率分配策略非常困难，因为符号个数要趋于无穷大。此外，求解使得频谱效率最大的功率分配策略也非常具有挑战性，因为首先是符号个数要趋于无穷，其次是不同的功率分配策略既影响容量的大小，也会影响发送信号的功率谱分布，从而导致频谱效率优化变得困难。因此，多径信道下FTN系统在时域或者频域的最优功率分配策略是重要的研究课题。此外，获知信道信息以及匹配滤波器参数的FTN系统可以在发送端进行预编码操作，以消除多径间以及符号间的干扰，从而提升系统的性能。但是预编码方案同样会影响容量和发送信号的功率谱分布，有效提升FTN系统频谱效率的预编码方案设计也是一个非常重要的研究方向。