基于非凸秩近似的大规模MIMO信道估计

张 琳，黄学军

（南京邮电大学通信与信息工程学院，江苏 南京 210003）

大规模多输入多输出（Multiple⁃Input Multiple⁃Output，MIMO）技术在基站（Base Station，BS）侧部署大量天线，通过空间多路复用，采用简单的最大比合并和最大比传输技术显著提高系统的吞吐量、可靠性和频谱效率［1-2］。为了实现这些优势，需要在BS端精确地获取到信道状态信息（Channel State Information，CSI）［2］。随着天线规模的增大，采用传统的CSI估计方法，例如，最小二乘（Least Square，LS）［3］和 最 小 均 方 误 差 （Minimum Mean⁃Squared Error，MMSE）［4］会浪费大量的导频资源。如何在降低系统导频开销和计算复杂度的同时准确有效地获取CSI是一个大规模MIMO系统相关研究中亟待解决的重要挑战。

为解决导频开销问题，通常考虑信道在角度域的稀疏性，利用压缩感知（Compressed Sensing，CS）技术进行有效的CSI估计［5-13］。文献［8-9］采用贪婪稀疏恢复算法进行CSI估计，这类算法相比传统的LS算法在低导频开销情况下具有更好的CSI估计性能，但没有考虑信道的联合稀疏性。文献［10-11］考虑信道矩阵在虚拟角度域中的联合稀疏性，进一步提高低导频开销下的CSI估计精度，但上述方法需要获取信道稀疏的先验信息，这在实际通信环境中不易实现。文献［12-13］提出一种稀疏自适应的CSI估计算法，适合信道角度域稀疏度未知的情况，但该算法对稀疏度变化敏感，且计算复杂度较高。上述基于CS的稀疏CSI估计方法虽然可以有效降低导频开销，改善CSI估计精度，但BS和用户之间的角度域稀疏性在实际环境中不易控制，并且在求解信道矩阵过程计算复杂度较高，限制了稀疏CSI估计在实际大规模MIMO系统中的应用。除了稀疏重构信道矩阵外，Candès等人提出当矩阵的秩较小时，通过凸优化的方法可以有效重构原始矩阵［14-15］。这类方法不需要考虑矩阵的稀疏性，直接利用低秩性进行矩阵恢复。文献［16-17］将低秩矩阵完整化的思想应用于大规模MIMO信道估计中，分别采用半定规划（Semidefinite Programming，SDP）和混合奇异值投影（Hybrid Singular Value Projection，SVP⁃H）算法在低训练开销情况下精确估计CSI。虽然上述两种算法CSI估计精度较高，但在求解信道矩阵的过程中都涉及矩阵求逆运算，计算复杂度较高。

为了提高低训练开销、低计算复杂度情况下的CSI估计性能，受物理有限散射信道模型中［16-17］信道矩阵秩较小的启发，本文考虑将低秩矩阵近似的方法应用到CSI估计中，采用非凸的γ⁃范数近似信道矩阵的秩函数来提高信道矩阵秩近似的精度。利用交替方向乘子（Alternating Direction Method of Multipliers，ADMM）算法进行CSI估计，对信道矩阵进行随机采样，选择其中较少的信道参数，有效降低训练开销。变量交替迭代更新的过程中采用梯度下降法避免了求逆运算，有效降低算法复杂度，通过选择较小的迭代步长，提高CSI估计精度。

1 系统模型

考虑一个由BS和K个单天线用户（UE）组成的大规模MIMO系统，BS配备M根均匀线性天线阵列（Uniform Linear Array，ULA），假设系统在频分双工（Frequency Division Duplex，FDD）模式下运行，BS在训练阶段通过下行信道发送长度为L的训练序列，K个UE接收到的信号Y∈CK×L表示为

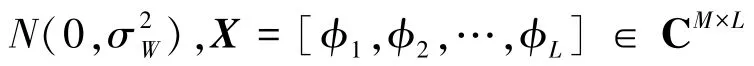
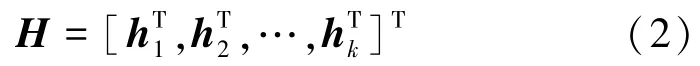
式中，信道向量 hk∈ C1×M，k＝1，2，…，K。考虑有限散射的物理信道模型［16-17］，在此模型中，角度域划分为有限的P个方向，该方向数目是固定的，且P与BS天线和UE数目无关［16-17］，BS和第k个用户之间的信道向量hk表示如下

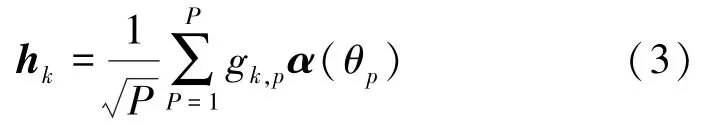
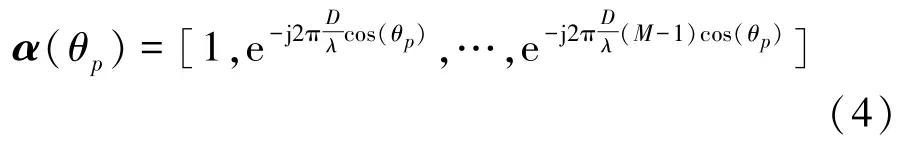
式中，G∈ CK×P，设其为加性复高斯矩阵，且G（k，p）＝gk，p。

A＝［（α（θ1）T，α（θ2）T，…，α（θp）T）］T∈CP×M，根据式（5）可知，rank（H）≤min（rank（G），rank（A）），即rank（H）≤min（M，K，P）。由于基站天线位置较高，周围散射体较少，因此角度域方向数目P ＜ min（M，K），故rank（H）≤P，即信道矩阵的秩远小于信道矩阵的维数。本文考虑在BS侧联合恢复CSI，用户反馈给BS的信号Z表示为

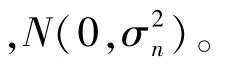
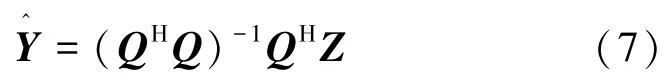
2 大规模MIMO系统低秩信道估计

2.1 低秩信道矩阵表示

由式（5）可知，信道矩阵H的秩较小，因此本文考虑将CSI估计问题转化为低秩信道矩阵完整化问题。为了便于求解信道矩阵的秩函数，文献［16］利用核范数近似信道矩阵的秩函数，BS侧联合信道估计问题转化为信道矩阵核范数最小化问题，即

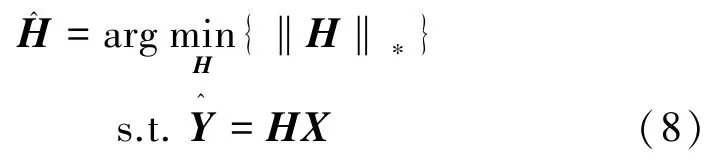
2.2 基于ADMM算法的低秩信道恢复

根据式（9）的约束条件，采用正则化的方法，将式（9）转化成无约束优化问题，信道估计矩阵满足

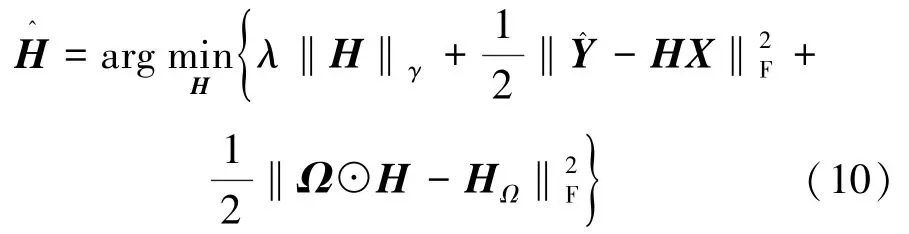
本文采用ADMM方法简化其求解步骤，引入新变量S，将式（10）目标函数中的一个变量分解成两个变量，进行并行计算。此时式（10）变为

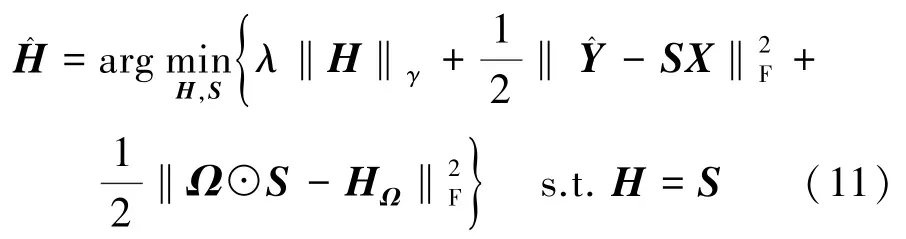
根据式（11），可以得到增广拉格朗日函数为

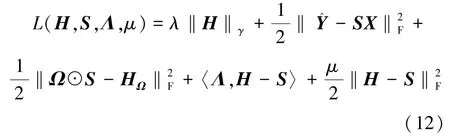
式中，λ＞0，Λ为拉格朗日乘子矩阵，〈Λ，H-S〉＝tr（ΛT（H-S）），μ 为ADMM 算法的罚参数。ADMM算法中各个参数的更新公式分别为［20］

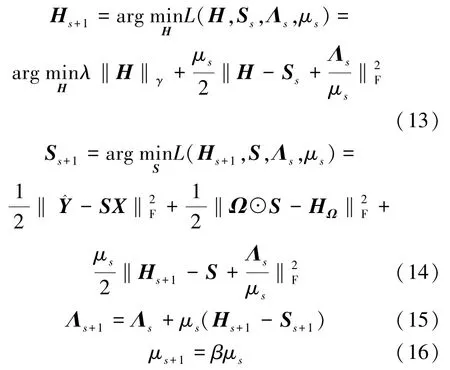
根据式（13）至（16）可知，ADMM算法更新变量包括更新H，S，Λ和μ 4个步骤。更新乘子矩阵Λ时利用罚参数μ作为步长，s为迭代次数。

首先求解H，H的迭代公式为

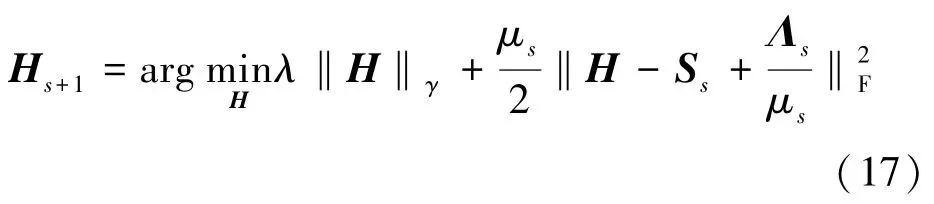
对式（17）中的 H求微分，‖H‖γ的微分定义为［19］

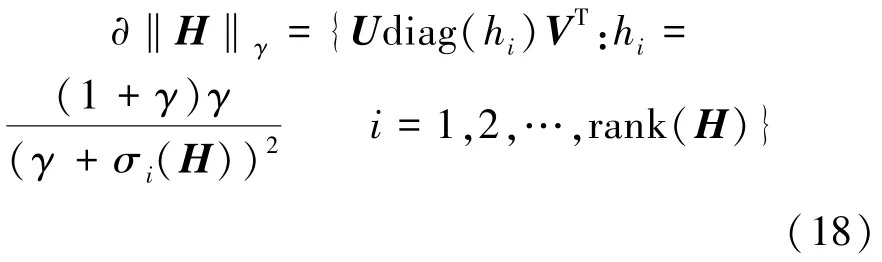
式中，U为H的左奇异值矩阵，V为H的右奇异值矩阵。

结合式（17）和（18），可得

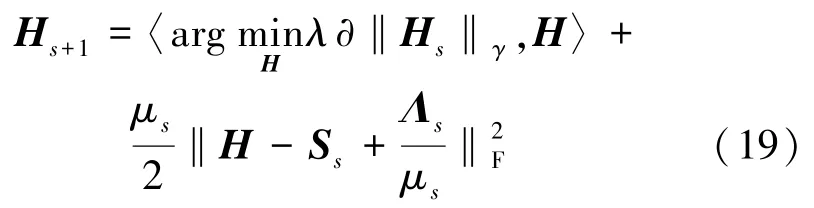
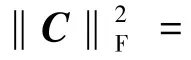
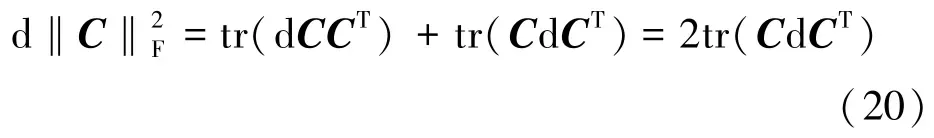
通过上述分析，可以得到式（19）中H的梯度为

令式（21）中∇H＝0，最终得到H的迭代公式为

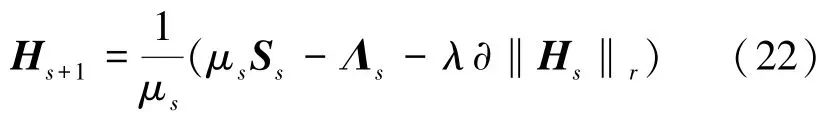
接下来求解S，S的迭代公式为

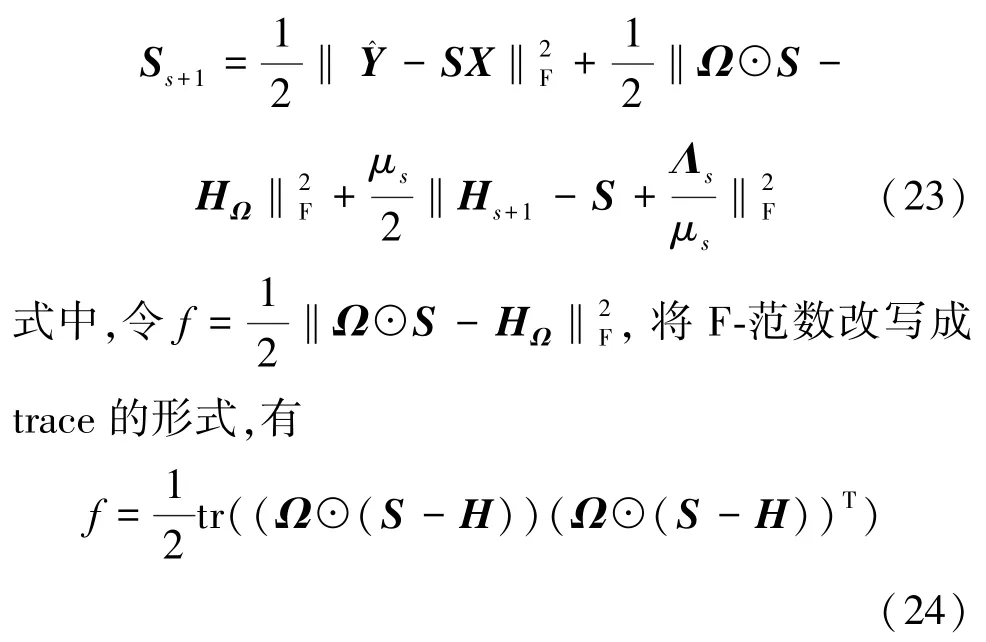
等号左右两边分别求微分，得到

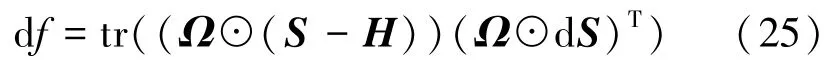
通过交换矩阵乘法和逐元素乘法，得到

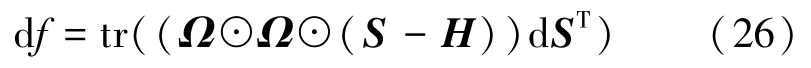
这里注意，Ω⊙Ω＝Ω，因此

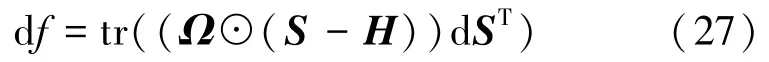
最后得到

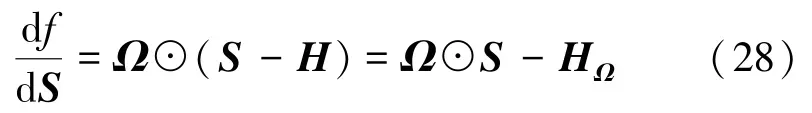
式（23）中S的梯度为

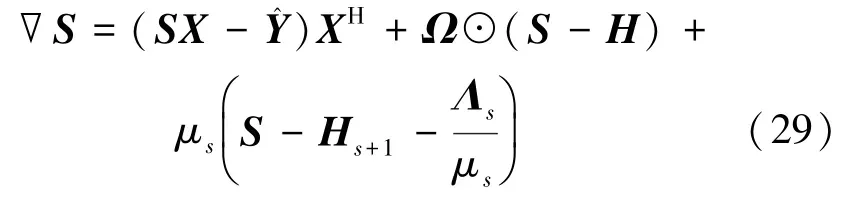
如果令式（29）中∇S＝0，求解S会涉及对X的求逆运算，计算复杂度会增加M3。为了减小计算复杂度，本文考虑采用梯度下降法更新S，梯度下降法公式为

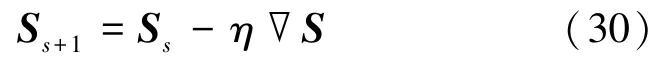
式中，η表示每次的迭代步长（0＜η ＜1），∇S则是由式（29）求出的S的梯度。

根据上述分析，基于ADMM的信道估计见算法1。

算法1 基于ADMM的低秩信道矩阵恢复

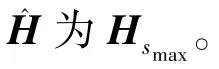
2.3 参数设置

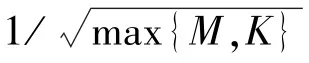
2.4 算法复杂度分析

算法1的计算复杂度主要取决于基站端天线数目M、用户数目K、信道矩阵的秩r、导频开销L以及最大迭代次数smax，ADMM算法在求解Hs+1的过程中需求解 ∂‖Hs‖γ，该过程需对 Hs进行奇异值（Singular Value Decomposition，SVD）分解，计算复杂度为Mr2，求解Ss+1时需要求解S的梯度，该过程仅涉及矩阵乘法运算，求解式（29）的计算复杂度为MKL+MK，更新Λ，μ的过程中是各个矩阵之间的加减运算，计算复杂度忽略不计。所以ADMM算法的计算复杂度为 O（Mr2smax+KMLsmax+MKsmax），ADMM算法将目标函数中的一个变量分解成两个变量，并且对两个变量进行并行计算，程序运行所需时间少。文献［17］提出的SVP⁃H算法的计算复杂度为 O（M2L+M3+KMLsmax+Mr2smax）。文献［18］提出的软阈值（Singular Value Thresholding，SVT）算法计算复杂度为 O（2KMLsmax+M（2P2+r2） +M3）。通过比较可知SVP⁃H和SVT在求解信道矩阵过程中都涉及矩阵求逆，而本文提出的ADMM算法不涉及矩阵求逆过程，计算复杂度相对较低。

3 仿真结果与性能分析

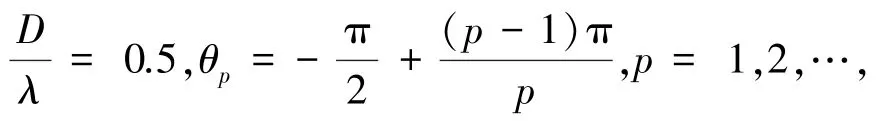
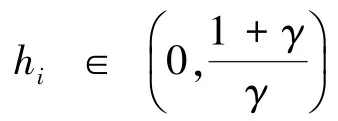
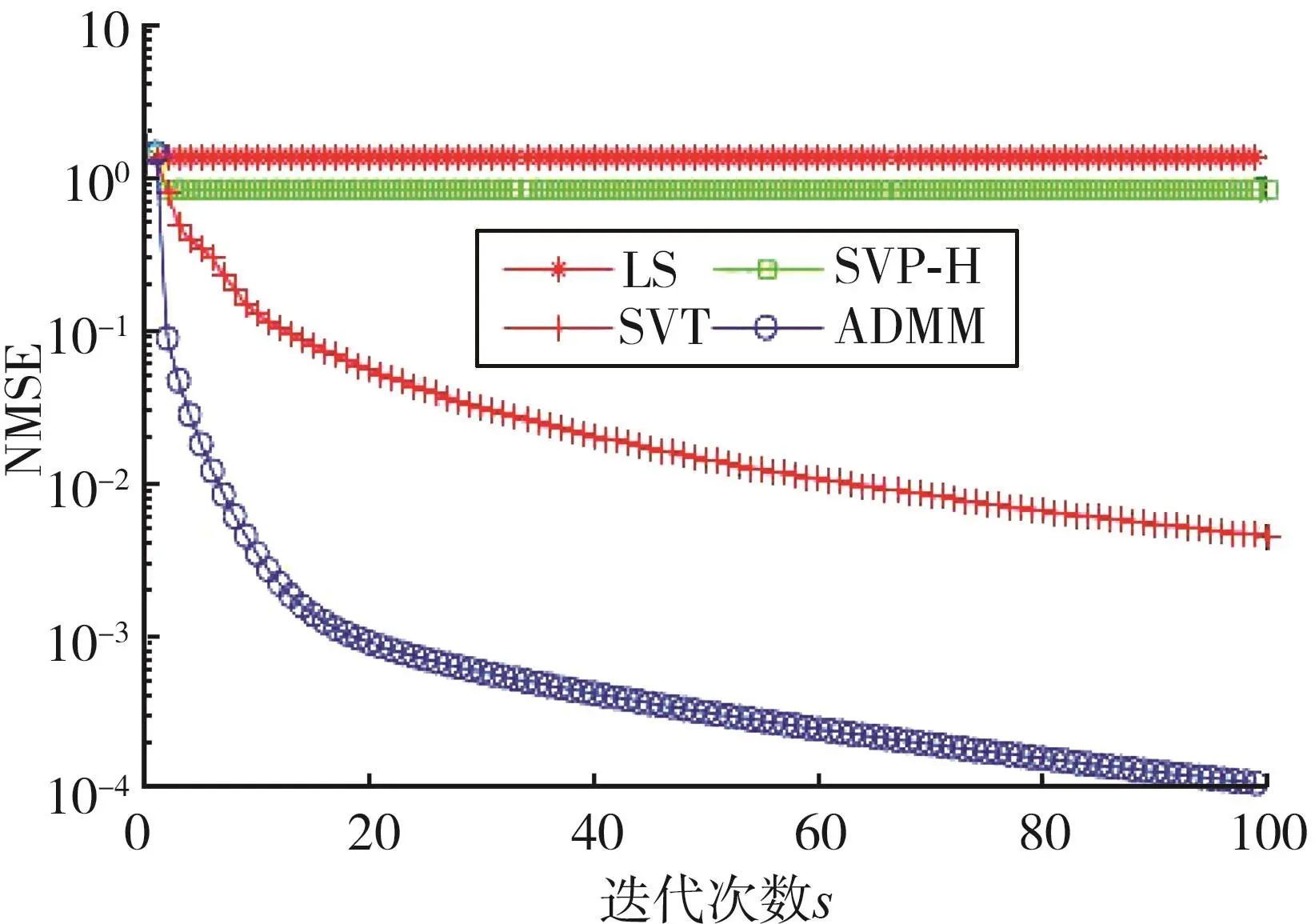
图1 估计性能随迭代次数的变化

图2比较了信噪比SNR对CSI估计性能的影响，SNR 分别取5，10，15，20 和25 dB，最大迭代次数smax＝50，其余参数取值与不同迭代次数s中的参数相同。由图2可知，SNR的大小对CSI估计性能影响较大，在SNR较小的情况下，噪声占据主导地位，CSI估计对噪声较敏感，SNR＝5 dB时，各个算法的CSI估计误差较大，当SNR增大时，各个算法的CSI估计性能有所提升。当SNR取值相同时，基于低秩矩阵恢复的SVP⁃H、SVT、ADMM算法的CSI估计性能优于LS算法，其中本文提出的ADMM算法在较低SNR情况下的CSI估计性能最佳。

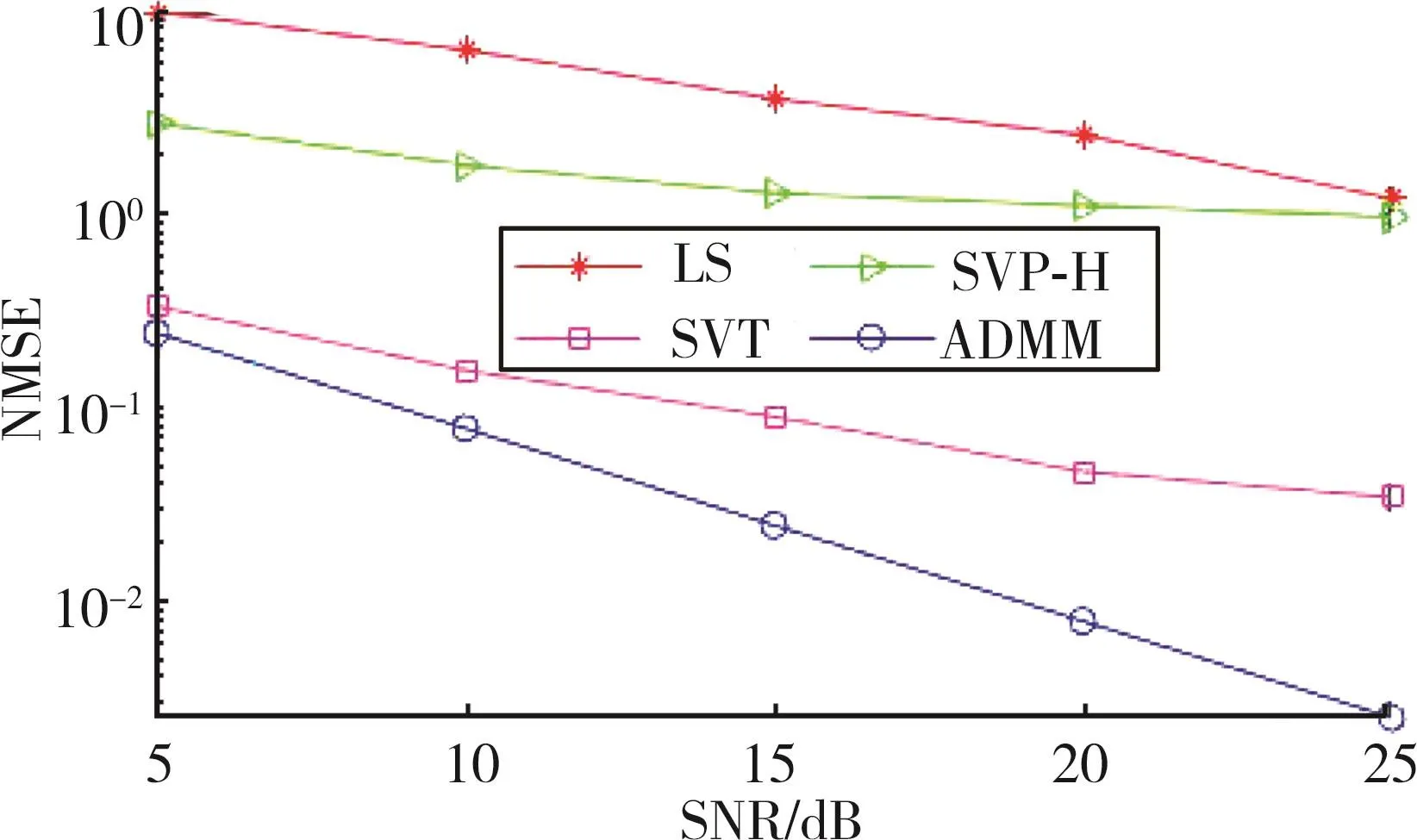
图2 估计性能随SNR的变化

图3比较了CSI估计的NMSE随着信道开销L的变化情况，信道开销L分别取为30、40、50、60和70，最大迭代次数 smax＝50，SNR＝20 dB，其余参数取值与不同迭代次数s中的参数相同。由图3可知，当L＝30时，LS算法的 NMSE＝0.8，SVT算法的NMSE＝0.05，ADMM 算法的 NMSE＝0.007，比较可知，LS在较少开销情况下的CSI估计性能较差，而文献［18］中的SVT算法和本文提出的ADMM算法的CSI估计性能优于LS，这是因为SVT和ADMM都是基于低秩矩阵恢复的算法，通过采样值对信道矩阵进行随机采样，利用其中较少的值进行CSI估计，因此可以在较少L的情况下得到较好的CSI估计性能。随着L的增加，各个算法的CSI估计性能均随之增加。在相同 L的情况下，本文提出的ADMM算法性能最佳，因此ADMM算法仅需较少的导频开销即可得到较好的CSI估计性能。

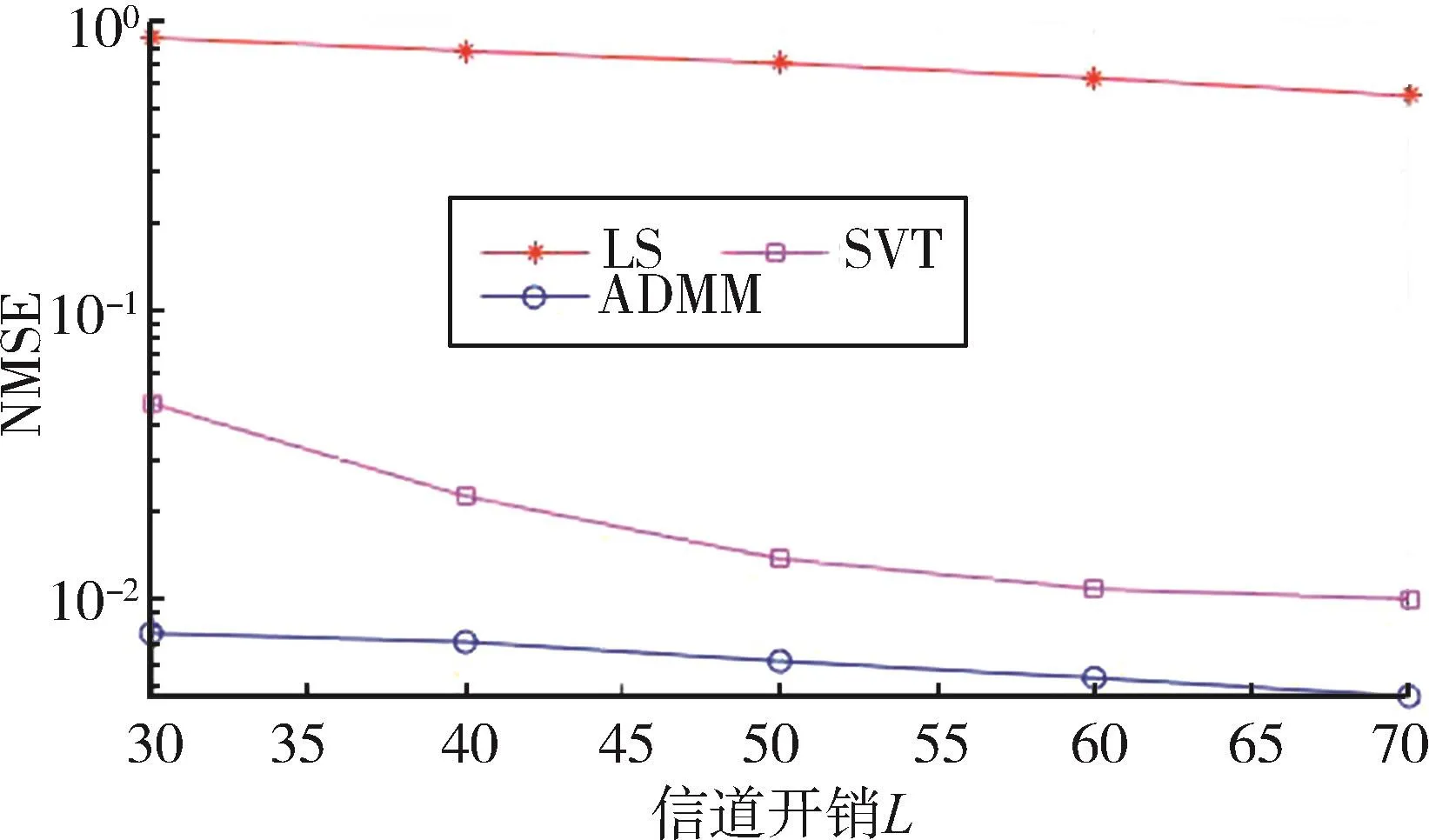
图3 估计性能随信道开销的变化

图4比较了信道矩阵在不同采样率samplerate和不同SNR情况下ADMM算法的CSI估计性能，信道矩阵的采样率是指矩阵中非0元素的比例。其中M＝100，K＝80，smax＝50。由图 4可知，随着 SNR 的增加，各个采样率的CSI估计性能都随之增加，噪声对CSI的估计性能影响较大，当samplerate＝10%，SNR＝5 dB时，CSI估计误差为0.3，当 SNR＝25 dB时，NMSE＝0.003。SNR相同的情况下，不同采样率对CSI的估计性能影响较小，当SNR＝5 dB，samplerate＝50%时，NMSE＝0.1，与 samplerate＝10%的估计性能相差0.2，当SNR＝25 dB，samplerate＝20%时，NMSE＝0.002 5，samplerate＝30%时，NMSE＝0.001 9。通过比较可知，SNR对CSI估计误差影响较大，不同采样率对CSI估计误差影响较小。

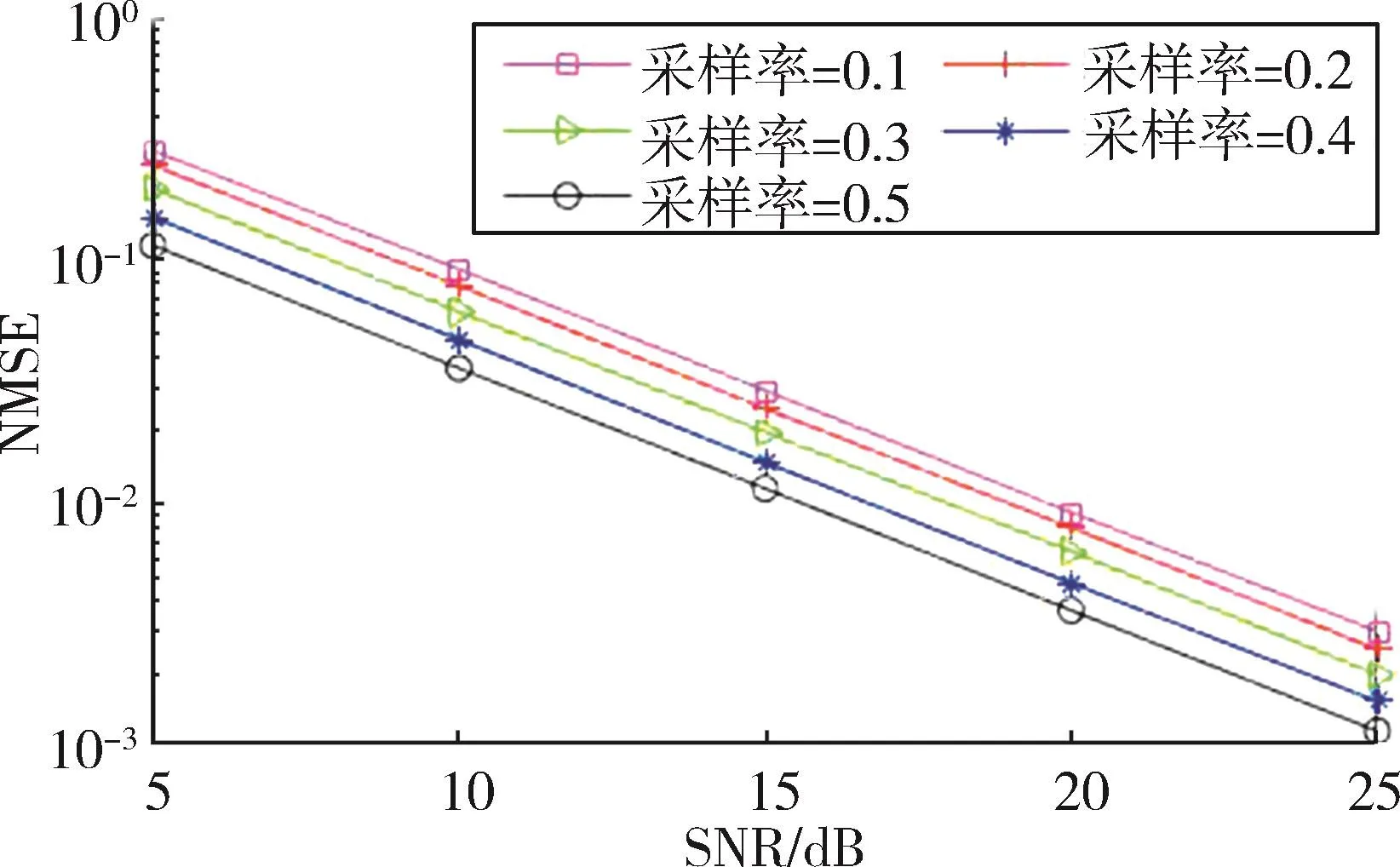
图4 所提算法的信道估计性能随采样率和信噪比的变化

4 结束语

为了减少大规模MIMO系统CSI估计过程中的训练开销，提高CSI估计性能，本文利用信道矩阵的低秩特性，提出低秩矩阵近似的CSI估计方法，采用非凸的γ⁃范数精确近似信道矩阵的秩函数，改善了信道矩阵奇异值较大时，核范数近似信道矩阵秩函数的缺陷。采用ADMM算法进行CSI估计，大大降低了计算复杂度，与 LS、SVP⁃H、SVT算法相比，所提算法在低训练开销、低信噪比情况下具有较好的CSI估计性能。