无人机协助边缘计算的能量收集MEC系统资源分配策略

陶丽佳，赵宜升，徐新雅

（1.福州大学物理与信息工程学院，福建 福州 350116 2.福州大学福建省媒体信息智能处理与无线传输重点实验室，福建 福州 350116）

射频（Radio Frequency，RF）能量收集是一种可从环境RF信号收集能量的技术，能为用户设备持续地提供能量［1］。然而，由于存在信号的衰减，用户在短时间内收集的能量较少。如何充分利用收集到的有限能量，是保证系统性能的关键。移动边缘计算［2］（Mobile Edge Computing，MEC）可以将用户的计算任务卸载给计算能力更强的边缘服务器，能够显著减少用户的能量消耗。另外，通过设计资源分配优化策略，可以高效使用收集的能量。因此，研究结合MEC的能量收集系统的资源分配问题，对提升系统性能具有重要意义。

能量收集MEC系统的资源分配问题已经引起了极大的研究兴趣。文献［3］利用基站（Base Station，BS）作为RF源，为具有RF能量收集功能的单用户提供能量，该BS也可为此用户提供MEC服务，用户使用收集到的能量进行本地计算或将任务卸载至BS，在用户能量收集和时延的约束下，以最大化用户给定任务计算成功的概率为目标。文献［4］在支持非正交多址的MEC无线供电系统中，建立非线性能量收集模型为用户提供能量，分别在部分和二进制卸载模式下，联合优化能量收集时间、计算频率、用户卸载次数和用户传输功率，使用户计算速率最大化。文献［5］将两个用户的无线MEC系统节能卸载和资源分配问题结合，基于时分多址机制下的收集⁃卸载协议，首先考虑保证用户的公平性提出了能源效率最大化，然后针对“双重远近”问题，提出了用户协作方案，离MEC服务器近的用户可以利用其收集到的能量，将远距离用户的任务转发到此边缘服务器，实现能量效率最大化问题。文献［6］研究了具有射频能量收集的多用户MEC系统中的能量管理问题，在带有电池队列稳定性和服务质量的约束下，将能量消耗最小化问题转化为随机优化规划问题，提出了一种基于李雅普诺夫的集中式能量管理算法。文献［7］研究了由一个接入点、多个移动设备和一个恶意窃听者组成的具有物理层安全的MEC系统，在保证计算任务成功完成和满足安全卸载约束的前提下，建立了关于本地计算和卸载计算的能耗模型，提出了能量消耗最小化的资源分配策略。文献［8］提出一种无人机（Unmanned Aerial Vehicle，UAV）支持的MEC系统资源分配框架，利用UAV为用户提供MEC服务；通过联合优化卸载时间、计算频率、用户发射功率和UAV轨迹，实现计算效率最大化。文献［9］研究了一种由多UAV辅助的多接入MEC模型，通过允许用户将任务卸载至UAV的多个MEC服务器上进行并行计算，从而使用户和UAV的能量消耗最小化。文献［10］中UAV为多个小区的边缘用户提供服务，考虑了UAV作为移动BS和地面BS之间存在的干扰，利用轨迹优化使UAV远离地面BS服务的用户，以减少干扰的影响；联合优化了UAV卸载时长和UAV轨迹，以最大化边缘用户吞吐量为目标。然而，现有研究假设边缘服务器有足够的计算资源，没有考虑到用户请求的计算任务超出边缘服务器计算能力的情况。当用户的计算任务超出边缘服务器计算能力上限时，如何为用户继续提供边缘计算服务，是亟待解决的问题。文献［11］考虑在无人机上搭载边缘服务器，为地面用户提供边缘计算服务，考虑到用户的服务需求，通过联合优化UAV轨迹、用户发射功率和计算资源分配，实现UAV能量效率的最大化。受文献［11］的启发，如果引入一个搭载边缘服务器的UAV，当用户请求的计算任务超出地面BS边缘服务器的计算能力时，将额外的计算任务转移给UAV边缘服务器，就可以保证为用户持续提供边缘计算服务。

本文针对用户请求的计算任务超出地面BS边缘服务器计算能力的问题，提出一种UAV协助边缘计算的最小化系统能量消耗的资源分配策略。通过部署一个携带MEC服务器的UAV，在用户的任务请求超出地面BS的计算能力时，为用户提供额外的计算资源，保证用户能在一定的时延要求下完成计算任务。用户将任务卸载至BS和UAV边缘服务器的同时，可从环境射频源中收集能量。综合考虑用户卸载计算任务和边缘服务器处理计算任务，将系统资源分配问题建模成一个最优化问题，以最小化系统能量消耗为目标，同时满足用户能量因果性、BS和UAV边缘服务器的计算资源以及用户发射功率的约束条件。该最优化问题是非线性规划问题，采用联合遗传算法和非线性规划（Genetic Algorithm and Nonlinear Programming，GANLP）方法获得最优解。最后，通过仿真对提出的资源分配策略进行性能评估。

1 系统模型

1.1 网络结构

具有RF能量收集功能的MEC系统网络结构如图1所示。该MEC系统中，包括I个用户和一个地面BS1，BS1上部署了 MEC服务器。由于地面BS1的MEC服务器计算能力有限，为确保用户能在一定的时延要求下完成计算任务，在BS1附近部署一个携带MEC服务器的UAV协助计算。UAV的高度固定为H。用户 i（i＝1，2，…，I） 可从环境 RF源收集能量。用户 i的坐标为 （xi，yi，0），BS1的坐标为 （xb，yb，Hb），UAV 的坐标为 （xq，yq，H）。第l（l＝1，2，…，L） 个 RF 源坐标为 （xl，yl，Hl）。因此，用户i和BS1之间的距离为

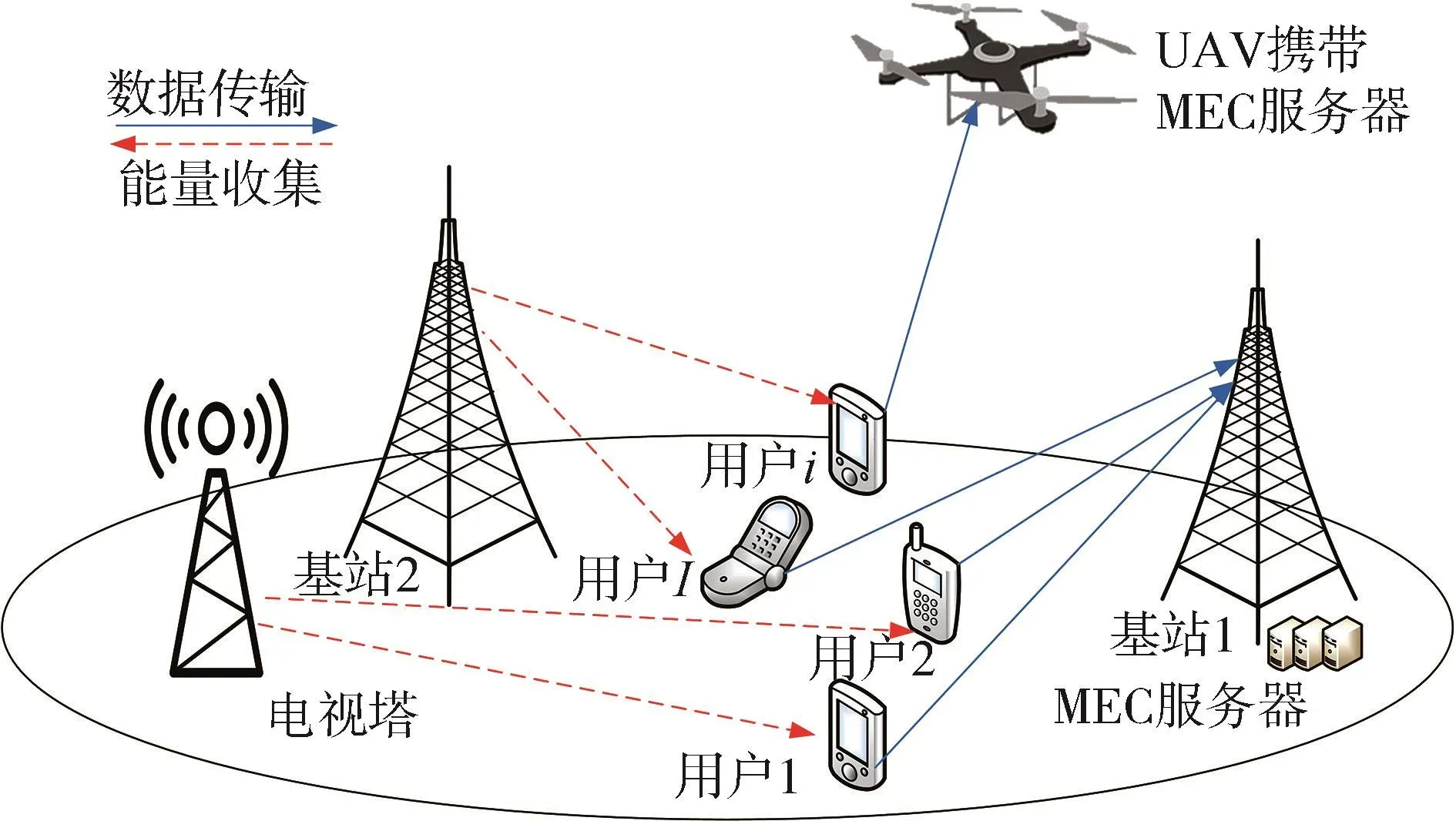
图1 UAV协助边缘计算的网络结构图

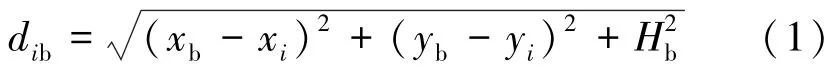
用户i和RF源l之间的距离为

用户i和UAV之间的距离为

用户计算任务卸载时序图如图2所示。用户将任务卸载至MEC服务器和MEC服务器计算用户任务都需消耗一定的时间，因此每个用户的计算任务会持续一段时间。假设BS1的MEC服务器能同时处理的最大用户数为n，每个任务只能在一个MEC服务器计算。当BS1的MEC服务器同时计算n个用户的卸载任务时，下一个用户将其计算任务卸载至协助计算的UAV处理。假设不同用户的任务产生间隔服从参数为λ的泊松分布，用户i的计算任务采用 Ui＝（Di，Ci，T） 表示，其中，Di为用户 i计算任务的数据大小，Ci为用户i计算任务需要的计算资源，T为用户i计算任务的时延约束。

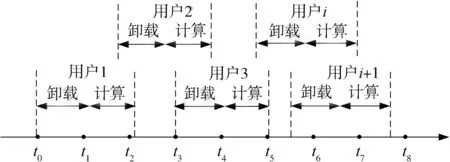
图2 不同用户的任务卸载和计算过程

1.2 用户能量收集模型

本节分析用户的能量收集模型。每个用户都配备能量收集电路，用户卸载计算任务的同时可从RF源收集能量。用户i附近的环境RF源包括电视塔和BS2。当用户i能量收集的时间为τ时，用户i收集到的能量为［12］

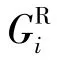
2 问题建模与求解

2.1 问题建模

针对上述系统模型，提出一种最小化系统能量消耗的资源分配策略。假设每个用户只有一个计算任务，但用户中央处理器主频较小，对于平均计算密度高的任务，本地计算时间长，易超出计算任务时延约束，因此本文将不考虑用户的本地计算。用户将计算任务卸载给计算能力更强的MEC服务器。通常，计算结果的数据量比开始上传时小很多，所以任务的计算结果返回时间远小于卸载时间和计算时间。因此，本文仅考虑用户任务卸载和MEC服务器处理用户任务阶段。

定义卸载调度ai＝｛0，1｝表示用户i的卸载决策，ai＝1表示用户i将计算任务卸载给BS1的MEC服务器，ai＝0表示用户i将计算任务卸载给UAV。此外，假设信道总带宽为B，分为I个子信道，定义σi为第i个子信道占用总信道的比例系数。MEC服务器与用户之间的信道以视距为主，无小尺度衰落［13］。

当ai＝1，用户i将计算任务卸载给BS1时，用户i与BS1链路的信道增益gib为

其中，β0是参考距离为1 m时的信道功率增益。用户i卸载计算任务至BS1的传输速率为

其中，pib为用户i将计算任务卸载给BS1的发射功率，N0为高斯白噪声功率。数据量大小为Di的任务卸载至BS1的传输时延为

同时，用户i将计算任务卸载至BS1的能量消耗为

假设fib为BS1分配给计算任务Ui的计算资源，即BS1的MEC服务器处理用户i任务的计算能力，则BS1处理用户i任务的计算时延为

同时，BS1计算消耗的能量为［14-15］

其中，Υ是一个和用户CPU类型相关的电容系数，Υ≥0。

当ai＝0，用户i将计算任务卸载给UAV时，用户i与UAV链路的信道增益giu为

用户i卸载计算任务至UAV的传输速率为

其中，piu为用户i将任务卸载给UAV的发射功率。数据量大小为Di的任务卸载至UAV的传输时延为

同时，用户i将任务卸载至UAV的能量消耗为

定义fiu为UAV分配给计算任务Ui的计算资源，则UAV处理用户i任务的计算时延为

同时，UAV计算任务消耗能量为

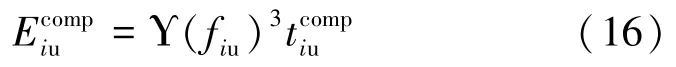
本文资源分配策略的目标是最小化系统能量消耗，同时满足一些约束条件。该优化问题可以建模为

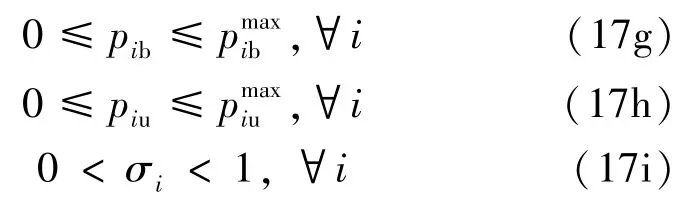
2.2 遗传算法和非线性规划优化

式（17）目标函数是自变量的非线性函数，约束条件也是关于自变量的非线性，因此式（17）为非线性规划问题，可通过结合传统GA和非线性规划求得全局最优解。GA是一种模拟生物界遗传和进化的人工智能优化算法［16］，对当前种群进行一系列遗传操作，包括选择、交叉和变异，可使得当前种群演化成更适合环境的下一代种群，最终种群将进化到包含近似最优解的状态。GA虽然具有良好的全局搜索能力，但局部搜索能力相对较弱，容易收敛至局部最优解，一般得到的是优化问题的次优解。非线性规划的局部搜索能力强，收敛速度相对较快，但是全局搜索能力不理想。因此，可通过GANLP对建立的优化问题进行求解。求解问题（17）的算法流程如图3所示。

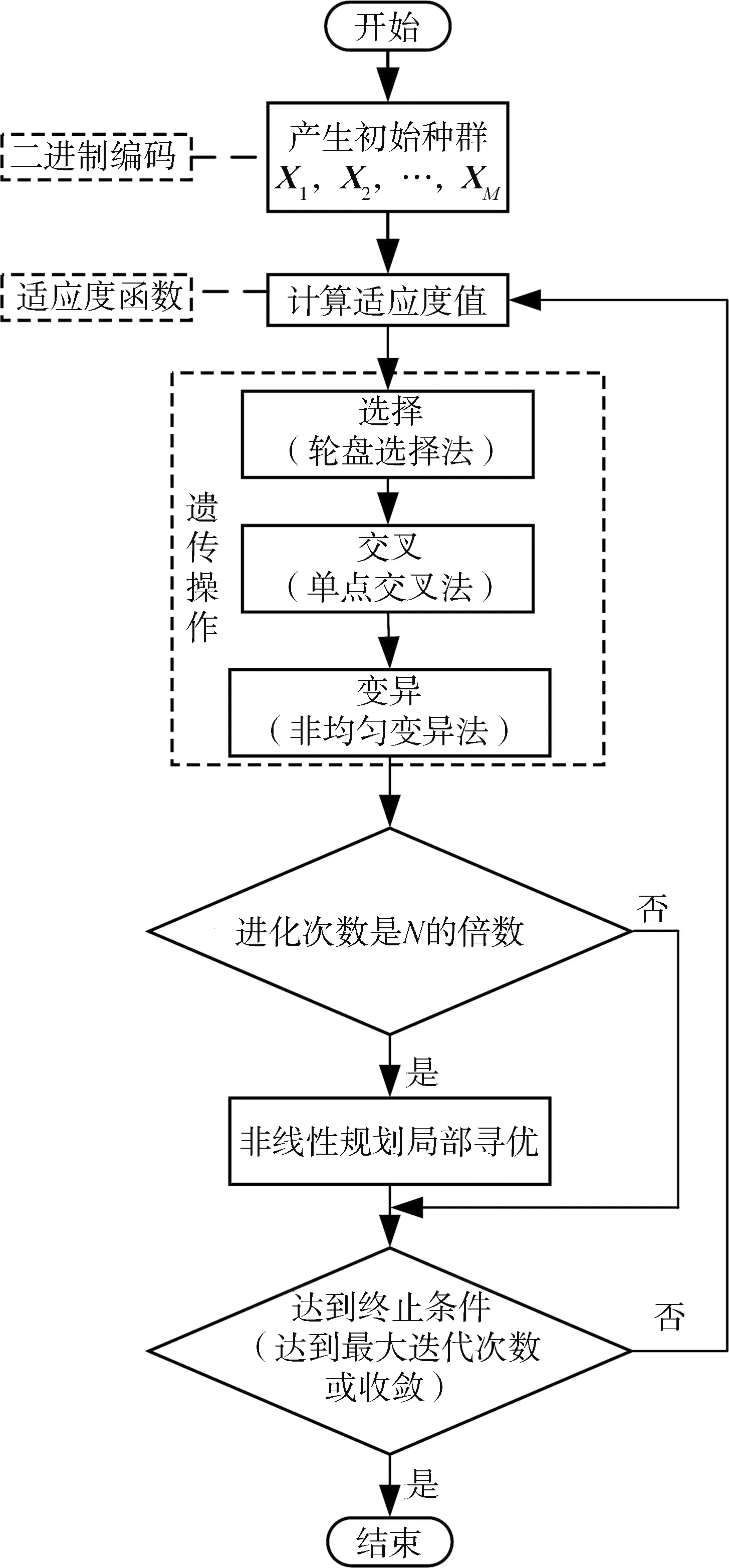
图3 GANLP方法流程图

首先，采用随机方式初始化种群，本文将采用二进制编码将变量参数编码为染色体。假设种群规模大小为M，将I个用户的发射功率、分配到的计算资源和子载波分配比例系数定义为个体的染色体，则个体m（m＝1，2，…，M）的染色体向量可以表示为

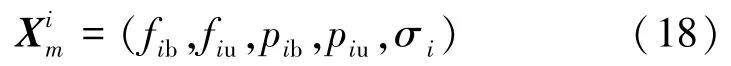
然后，根据生成的适应度函数计算适应值。为保证遗传操作生成的染色体是有效的，通过惩罚函数法将式（17）中有不等式约束的非线性问题转化成无约束问题［17］，因此适应度函数由目标函数和惩罚函数构成，表达式为

其中，fobj（fib，fiu，pib，piu，σi） 为目标函数；ξ是惩罚因子；fpen（fib，fiu，pib，piu，σi） 为惩罚函数，其包含了以下9个式子

其中，max（·，·）得到两个数值之间较大数的值。

接着，基于适应度值选取重组个体，采用轮盘选择法进行选择。个体被选取的概率与适应度值有关，适应度值越高的被选取概率越大。再采用单点交叉法对重组个体进行交叉操作，使得两个配对的染色体在其交叉点处相互交换其部分染色体。然后采用非均匀变异法对交叉后得到的新个体进行变异操作，改变新个体的某个或某些位值。再判断当前进化次数是否为N的倍数，如果是则采用非线性规划进行局部寻优；否则判断是否满足终止条件，若满足则可得到全局最优解。

为得到全局最优解，本文将GA和非线性规划结合。在采用GA进行全局搜索的同时，判断GA当前的迭代次数是否为N的倍数，如果满足条件，则将此时的种群作为初始值，采用非线性规划的外罚函数法进行局部搜索寻优，以得到全局最优解。具体实现流程如下。

步骤1：将有约束极值转化为无约束极值的辅助函数，数学模型如下：

其中，fobj（fib，fiu，pib，piu，σi） 为目标函数，Mk是惩罚因子。fpen（fib，fiu，pib，piu，σi） 是惩罚函数，惩罚函数对应了9个约束条件，表达式与式（20）中的约束条件相同。

步骤2：当迭代次数为N的倍数时，将此时的种群个体作为迭代的初始值 X（0），X 包含 fib、fiu、pib、piu和σi5个自变量，放大系数q＞1，允许误差ε＞0，置k＝1。

（1）计算最速下降方向，即搜索方向，沿着负梯度方向进行搜索

（2） 从 X（k-1）出发，沿 d（k-1）的方向对种群初始值进行搜索，应先求出步长sk-1，步长sk-1满足

（3） 由 X（k）＝X（k-1）+sk-1d（k-1）可得到极值点X（k）。

步骤 4：检验迭代准则，若 Mkfpen（X（k））＜ε则停止迭代，得到的X（k）为最优解，把寻找到的局部最优值作为新个体染色体继续进化。否则，Mk+1＝qMk，k＝k+1，继续迭代。

为了更加清晰地说明基于GANLP方法的最小化系统能量消耗资源分配策略，其具体步骤如算法1所示。

算法1 基于GANLP方法的最小化系统能量消耗资源分配策略

①初始化种群：随机生成M个个体的初始种群，允许误差ε。

②评价种群：基于式（19）计算当前种群的适应度值。

③进行遗传操作：首先，采用轮盘选择法进行选择操作；然后，采用单点交叉法对重组个体进行交叉操作；最后，采用非均匀变异法对交叉后得到的新个体进行变异操作。

④判断迭代次数：判断当前迭代次数是否为N的倍数，如果是则进入步骤⑤进行非线性规划寻优，否则返回步骤②。

⑤重复计算：将当前迭代次数的种群个体作为迭代的初始值X（0），利用最速下降法重复计算。

⑥ 基于式（22）计算最速下降方向dk-1。

⑦ 基于式（23）计算步长sk-1。

⑧ 基于 X（k）＝X（k-1）+sk-1d（k-1）得到极值点 X（k）。

⑨ 检验迭代准则：若 Mkfpen（X（k））＜ε则进入步骤⑩；若Mk+1＝qMk，k＝k+1则返回步骤⑤。

⑩检验终止条件：若当前进化代数达到最大进化代数，则算法停止，输出最佳适应度值；否则，返回步骤②。

3 仿真结果与分析

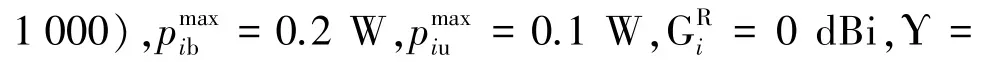
在仿真中，将提出的方法与以下4种方法进行性能对比。第一种方法为基于GANLP的功率分配策略（Power Allocation Strategy Based on Genetic Algorithm and Nonlinear Programming，P⁃GANLP），在此方法中，仅有用户的发射功率采用GANLP方法进行优化，其他自变量为固定值（即 fiu＝108cycles/s，σi＝0.3，fib＝109cycles/s）。第二种方法为基于GANLP的计算资源分配策略（Computing Resource Allocation Strategy Based on Genetic Algorithm and Nonlinear Programming，R⁃GANLP），在此方法中，仅有用户的计算资源采用GANLP方法进行优化，其他自变量为固定值（即 σi＝0.3，pib＝0.1 W，piu＝0.05 W）。第三种方法为基于GANLP的子载波分配策略（Sub⁃carrier Allocation Strategy Based on Genetic Algorithm and Nonlinear Programming，C⁃GANLP），在此方法中，仅有用户的子载波分配比例系数采用GANLP进行优化，其他自变量为固定值（即 pib＝0.1 W，piu＝0.05 W，fib＝109cycles/s，fiu＝108cycles/s）。第四种方法为所有自变量（即 fib，fiu，pib，piu，σi） 采用 GA进行优化，简称为GA。

图4给出了GANLP方法中种群数量和迭代次数对系统能量消耗的影响。从图4中可以看出，在相同的迭代次数下，随着种群数量从20逐渐递增到80时，系统能量消耗逐渐减小。这是因为种群数量越多，全局搜索性能更佳，结果更接近最优值。同理，在相同的种群数量下，随着迭代次数从200逐渐递增到1 000时，系统能量消耗也逐渐降低，最终趋于稳定状态，但系统能量消耗的大小有一定程度的波动。例如，当种群规模为20时，迭代次数为200的系统能量消耗比迭代次数为400的更小。这是因为遗传操作中的变异、交叉过程会使得最佳适应度值具有一定的随机性，但种群最终都会朝着更适合生存的方向进化。当种群数量为60，迭代次数为1 000左右时，系统能量消耗达到最小。因此，在接下来的仿真中，将种群数量和迭代次数分别设置为60和1 000。

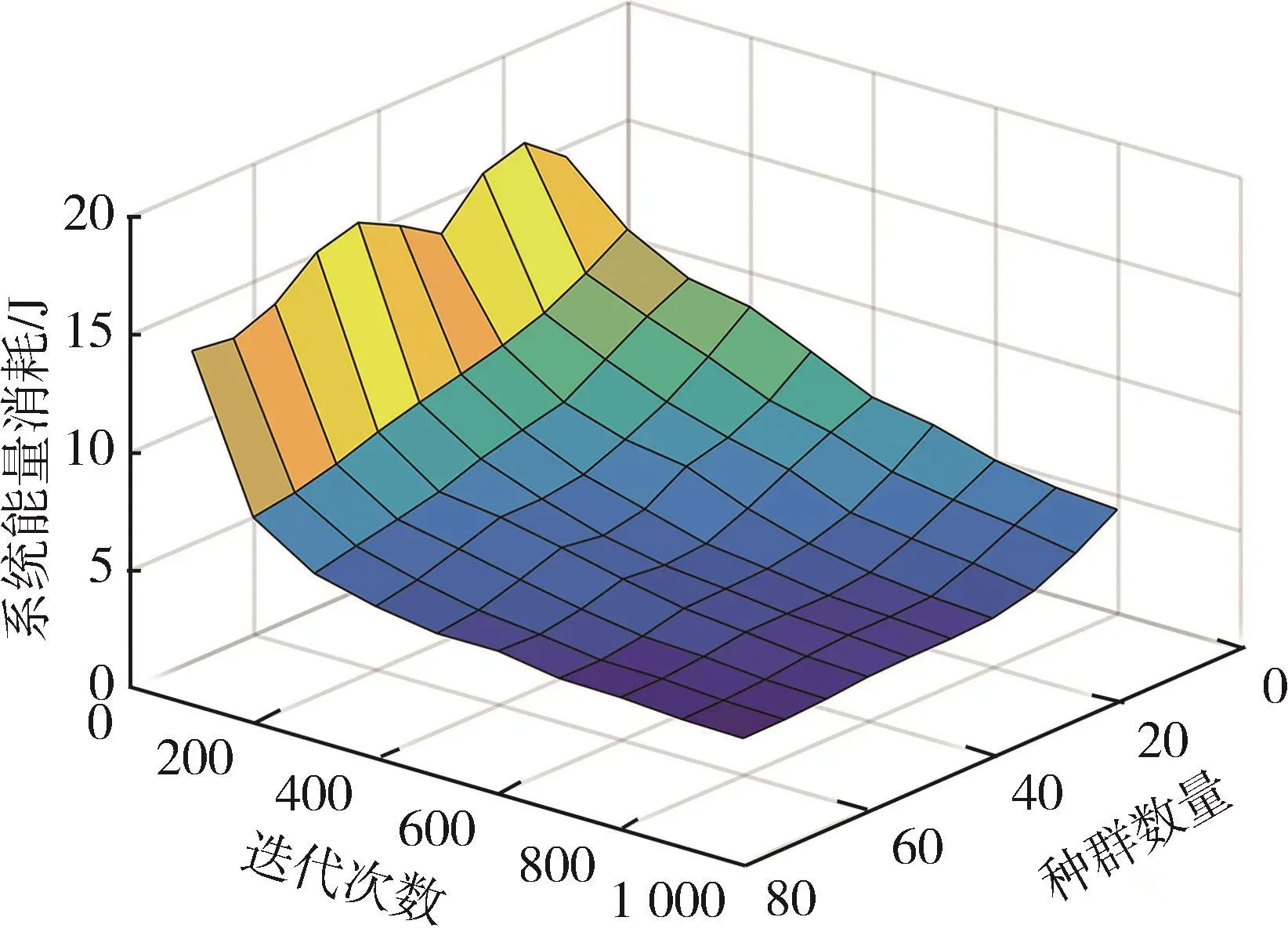
图4 GANLP中种群数量和迭代次数对系统能量消耗的影响

图5对比了不同用户数量在不同能量收集效率下的能量收集情况。从图5中可以看出，相同的用户数量下，随着能量收集效率从0.5增加到0.7，用户收集的总能量也随之增加。这是因为能量收集效率越高，将RF信号转换为直流电压获得的电能越多。此外，在相同的能量收集效率下，随着用户数量从20增加到30，所有用户收集的总能量也逐渐增多。当η为0.7，用户数量为30时，用户收集的总能量仅为14 J。这是因为RF源和用户之间的距离较远，电磁波在传播过程中存在损耗，导致用户的接收功率较小，因此用户收集的总能量较小。

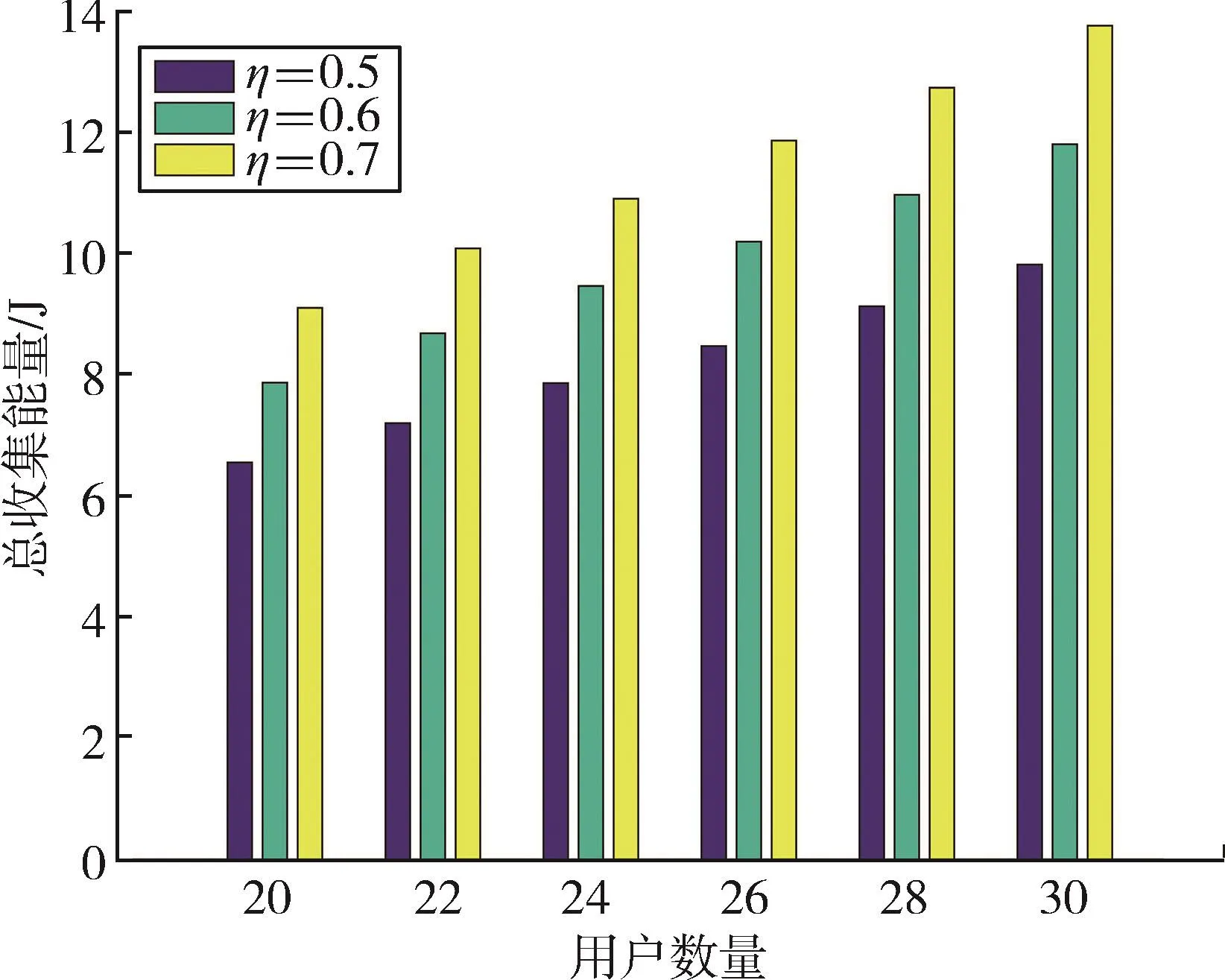
图5 不同用户数量时，不同能量收集效率下的能量收集情况

图6对比了传统GA和本文提出的方法GANLP的收敛性。从图6中可以看出，在相同的迭代次数下，GANLP系统能量消耗更小。这是因为传统GA容易出现早熟现象，陷入局部最优解，而非线性规划具有很强的局部搜索能力，搜索得到的结果更接近最优值。此外，还可以看出，GANLP经过600次迭代后，逐渐收敛至最优解，而传统的GA经过900次迭代后，才得到了局部最优解。因此，GANLP的收敛速度和寻优结果都优于GA。

图6 两种算法收敛性对比

图7对比不同方法下用户数量和系统能量消耗的关系。从图7中可以看出，当用户数量从36逐渐增加到52时，5种方法得到的系统能量消耗值都有所增加。一方面是因为各个用户卸载计算任务至MEC服务器时消耗一些能量，用户数量越多，系统消耗的能量就会随之增多；另一方面是因为MEC服务器处理用户计算任务也会消耗一些能量，用户数量越多，计算任务越多，系统能量消耗也会随之增多。此外，GANLP系统能量消耗始终低于 P⁃GANLP、R⁃GANLP、C⁃GANLP 和 GA。这是因为，相对于固定发射功率、计算资源或子载波分配比例系数，GANLP同时对发射功率、计算资源和子载波分配比例系数进行搜索，具有更好的优化能力。同时，相对于传统GA，GANLP具有更强的局部搜索能力，搜索所得到的结果将会更接近最优解。

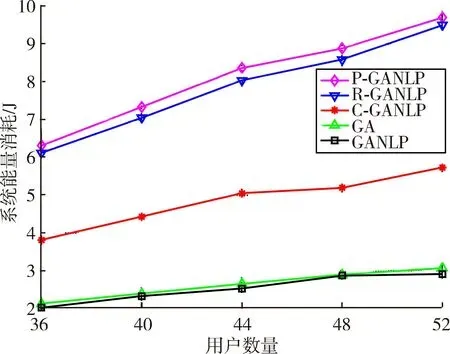
图7 用户数量和系统能量消耗的关系

4 结束语

本文针对现有研究没有考虑地面BS边缘服务器计算资源有限的问题，研究了UAV协助边缘计算的资源分配策略。通过部署携带MEC服务器的UAV，持续为用户提供边缘计算服务。超出地面BS边缘计算服务器处理能力阈值的用户，可卸载计算任务至UAV进行计算，以保证所有用户能在时延要求下完成任务。联合考虑用户和MEC服务器的能量消耗，将资源分配问题建模为非线性规划问题，在满足能量因果性、计算资源和发射功率的约束条件下，最小化系统能量消耗。通过引入GA结合非线性规划的方法获得最优解。仿真结果显示，GANLP全局搜索能力优于 GA算法。此外，相对于 P⁃GANLP、R⁃GANLP 和 C⁃GANLP，GANLP 具有更低的能量消耗。由于假设每个用户仅有一个计算任务且用户本身未参与计算，未来将针对用户具有多种计算任务，同时考虑用户本地和MEC服务器联合计算，对资源分配问题进行进一步研究。