基于收益权重的多期投资组合优化模型
胡晨阳,高岳林,2
(1.北方民族大学数学与信息科学学院,宁夏银川 750021;2.北方民族大学宁夏科学计算与智能信息处理协同创新中心,宁夏银川 750021)
在现今经济迅速发展的时代,人们对持有资产的分配方式不再局限于银行存储,更多人选择资产投资以增加其财富。最初对投资组合的研究可以追溯到Markowitz对单周期投资组合选择问题所提的MV模型的研究[1]。进而,Gordon J等[2]将风险价值(VaR)与均值-方差分析相联系,检验用均值-VaR模型进行投资组合选择的经济意义。
实际经济活动中,投资者会在不同时期重新分配自己的资产来优化投资策略,以规避风险,求得最终财富最大化。因此,许多学者都将这种经典的单周期均值方差投资组合模型扩展到多周期投资组合选择里。如Yan等[3]用半方差代替方差,提出了多阶段-半方差投资组合优化模型。Gao Jianjun等[4]考虑时间基数约束构建均值方差动态组合选择问题,通过对不同基数的求解,可以有效地解决带管理费的MV动态投资组合选择问题,从而制定最佳的择时策略。Zhang Peng等[5]用可能性绝对偏差控制风险,提出考虑多种摩擦因素的多期投资组合模型,用离散近似迭代法求解。
Mehlawat M K等[6]考虑熵作为风险度量,利用模糊收益的可信度熵对投资组合风险进行量化,利用离散选择和区间两种方法建立了基于可信度的财务目标多选择期望层次模糊优化模型,并采用一种嵌入多选择目标规划的模糊可信规划方法验证模型。Brandtner M等[7]进行了相关熵风险度量(CERM)和凸熵风险度量(ERM)两种熵风险度量下的比较静态分析,分析存在独立背景风险时的有风险与无风险组合问题,发现在CERM下,引入背景风险时,最优风险投资总是增加而不是减少,而在ERM下,它仍然不受影响。AksaraylM等[8]提出一种基于均值-方差-偏度-峰度-熵模型的多项式目标规划模型,并通过实验验证模型有效。Jadhao G等[9]使用样本熵和近似熵指标探索基于风格、规模和时间水平的组合轮换策略的可行性。Deng X等[10]用熵度量风险,建立基于可信度理论的模糊均值平均熵模型,对最大化收益模型和最小化风险模型中目标函数系数和约束系数的敏感性进行分析并验证其实用性。
传统的MV模型假设收益率服从正态分布,但收益率不能完全满足假设,就会导致最终结果不能准确应用到实际投资中。江璐瑶[11]考虑方差度量风险的局限性,构建均值-熵模型,其中收益率期望用每个时间段收益占总时间段收益权重计算,并通过实验验证收益权中的合理性及模型的有效性。熵衡量的是系统偏离均匀分布的程度,是一种宏观层面的风险度量,所以单纯用熵度量风险会存在一些盲点。鉴于此,本文在引入收益权重的基础上,建立可能性均值-下半方差-熵多期投资组合优化模型,相较于单风险测量模型。本文所建模型能够在考虑宏观和微观两个层面的风险的同时确保获取超额收益,且能更大程度规避风险。利用模糊决策理论和多目标规划方法,将模型转化为清晰的非线性规划问题,用改进的遗传算法进行求解。
一、基本概念
定义1[12]设模糊集∈F(U),任意γ∈[0,1]的,那么:
定义 2[12]设=(a,b,α,β)为梯形模糊数,带风险态度的梯形模糊数的隶属度函数定义为:
k是大于0的实数,被看作是风险态度的适应值。求解式(2)隶属度函数的导数可知,k越小,投资者就越厌恶风险,越想要逃避该风险。
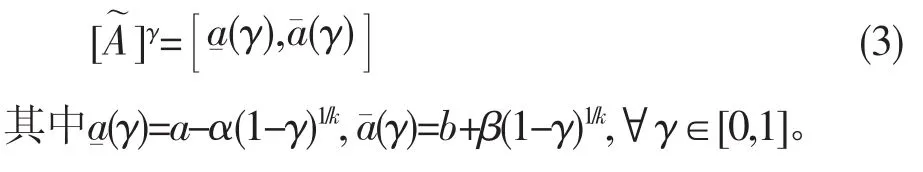
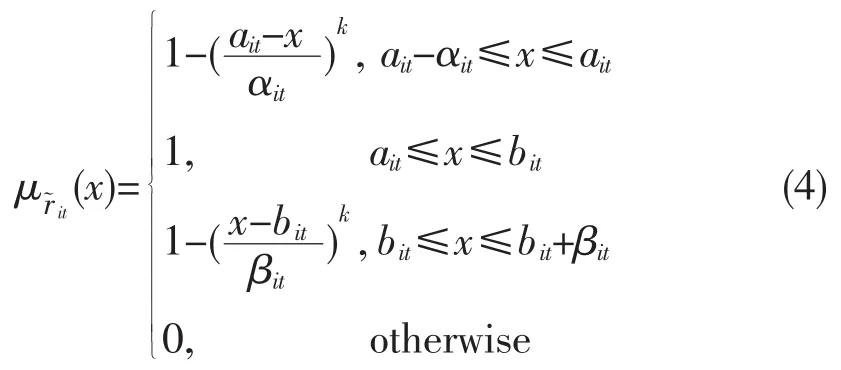
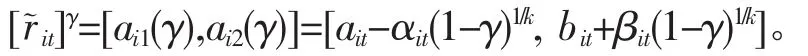
定义3[15]设模糊数,在γ-水平截集下的可能性均值、下半方差为:
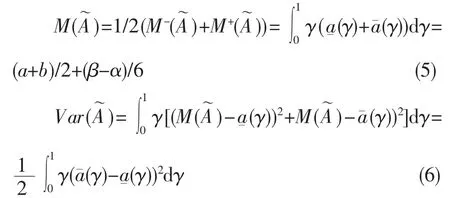
定义 4[16]设=(a,b,α,β)是梯形模糊数,由的γ-水平截集可以推出的可能性下方差为:
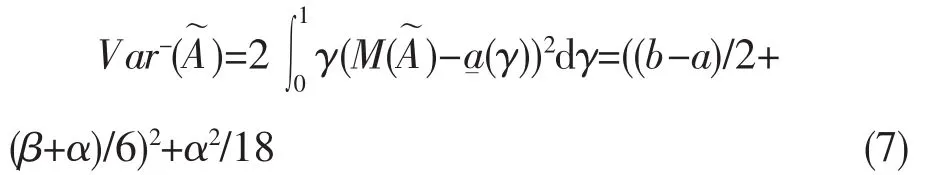
假设进行一个有n种结果的随机试验,假定出现每种结果的离散概率为Pi,信息熵[17]为:
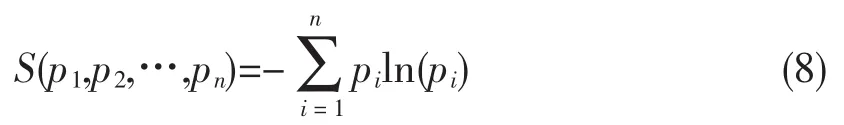
其中pi为样本出现的概率。
一般用熵来衡量投资组合的分散化程度,熵有以下性质:
2.可加性:在互相独立的事件中,和的熵与熵的和相同。
3.极值性:当每个样本的发生概率相等时,熵为最大值。
4.凹凸性:S(p1,p2,…,pn)为所有变量的对称凹函数。
二、可能性均值-下半方差-熵多期投资组合模型建立
设有n种风险资产,令收益权重θt代表在第t个时间段的收益占T个总时间段总收益的比例,rit为第i种资产对应于第t个时间段的收益率,则第i种资产的期望收益率i为:
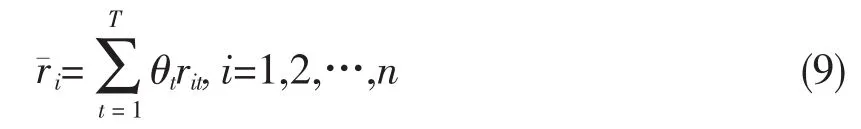
同时考虑资产不允许卖空,则有如下约束:
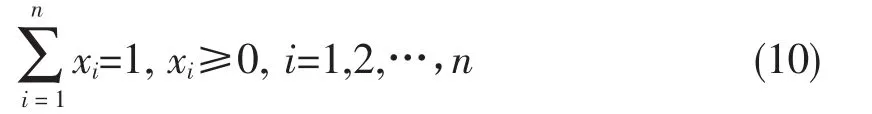
第t个阶段的收益Rt为:


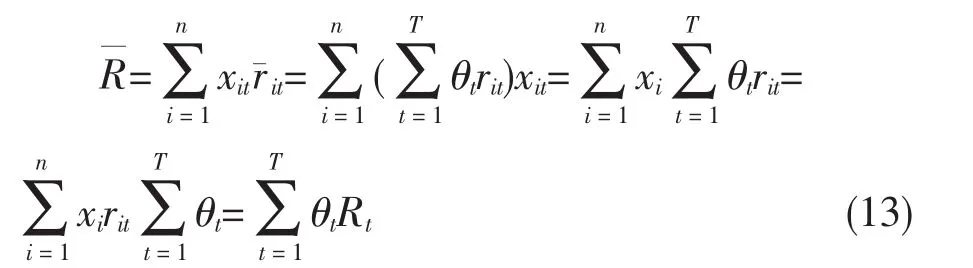
交易成本用V型函数表示,投资组合在t(t=1,2,…,T)时期的交易成本率可以表示为:

考虑交易费用和无风险资产的投资组合的下半方差为:
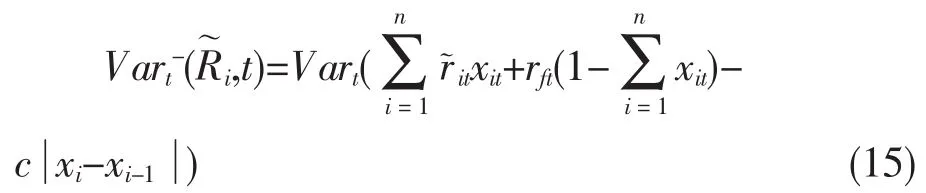
分散性的投资可以有效降低风险,Kapur利用比例熵对各时期投资组合的多元化程度进行度量[18]。本文引用了Kapur对多元化程度进行测度的方法,可以知道第t时期的多元化程度可以表示为:
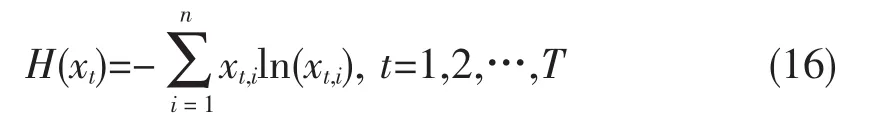
引入收益权重 θt,式(16)可转化为:
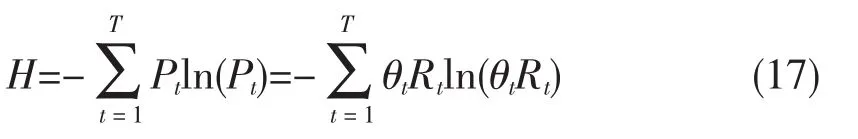
基于式(9)~式(17),建立含无风险资产的可能性均值-下半方差-熵多期投资组合模型如下:
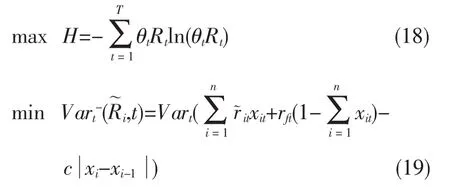
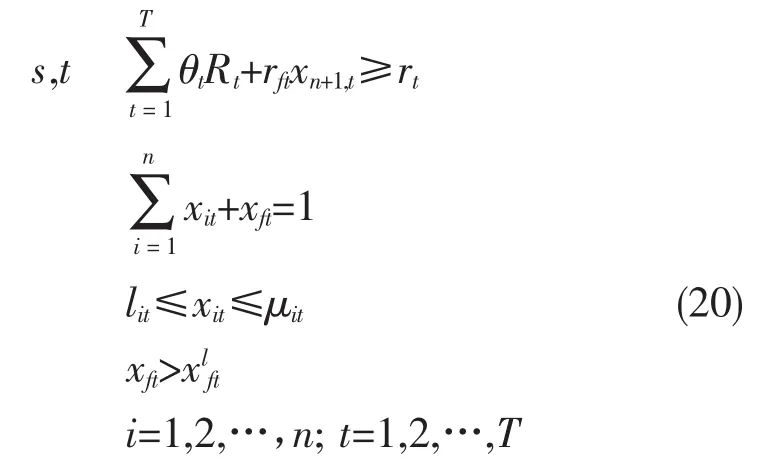
引入参数λ将式(18)~式(20)转化为单目标线性规划模型:
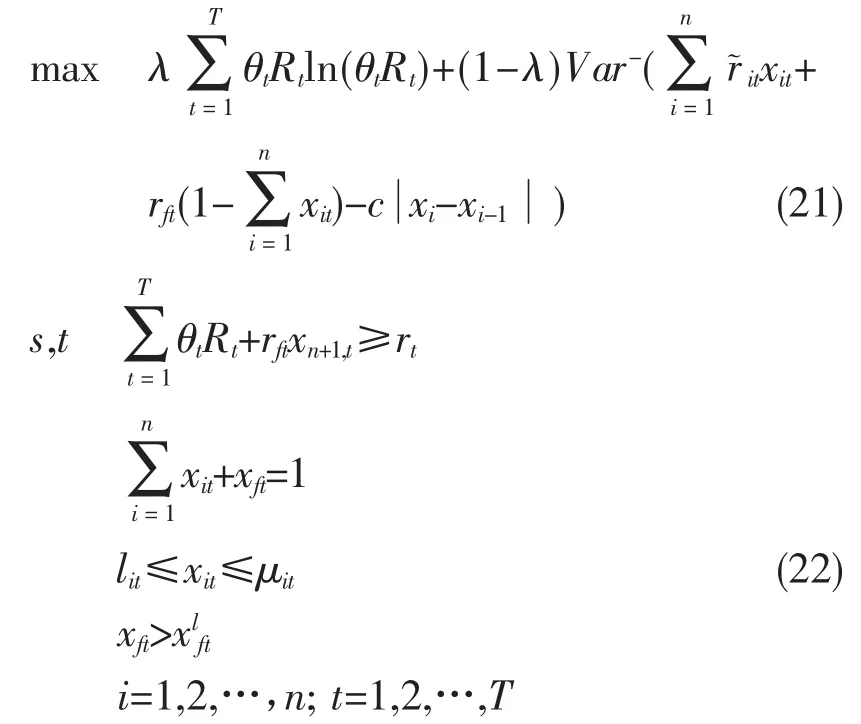
由于单目标线性规划模型中含有不等式约束,这种情况一般是非常难求解的。所以本文用外点罚函数法将不等式约束和等式约束放入目标函数中,将模型转变为无约束优化问题进行求解,转化后的模型为:
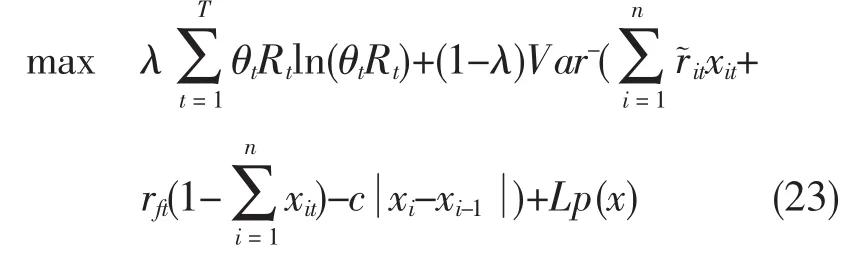
其中惩罚函数列P(x)为:
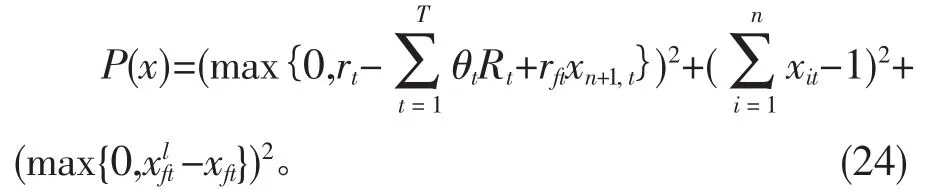
三、可能性均值-下半方差-熵多期投资组合模型算法改进
(一)遗传算法
遗传算法(Genetic Algorithm,GA)最早是由美国的John holland在20世纪70年代提出的,是一类借鉴生物界的进化规律(适者生存,优胜略汰遗传机制)逐步演化而形成的一种随机搜索方法。该算法通过数学的方式,采用计算机的仿真运算将问题的求解过程转换成类似生物进化中染色体基因的选择、交叉、变异等过程,被广泛应用于求解一些相对复杂的组合优化问题。该算法相较于其他一些常规的优化算法,在得出较好的优化结果方面速度更快。
1.logistic映射产生初始种群
采用十进制实数编码方式随机生成一个D维向量,每一个染色体作为一个实数向量,然后利用logistic映射生成非周期的、不收敛的,对初始值非常敏感的混沌序列,logistic映射公式为:

其中,μ∈[0,4],μ为映射参数。利用混沌序列产生初始种群有助于跳出局部最优,实现全局平衡,同时加快收敛速度,且会得到比伪随机数进行计算更好的效果。
2.适应度函数
适应度函数是区分个体优劣的标准。本文适应度函数为:
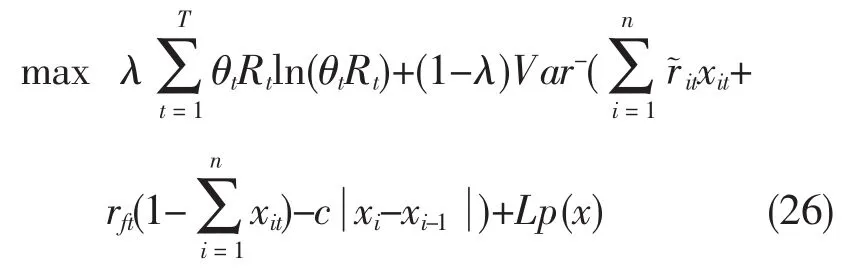
3.选择操作
在上一代种群中以一定概率选择优良个体组成新个体。用轮盘赌方式选择个体,保证优良个体产生下一代,个体i被选中的概率为P(xi)=Fi/ΣFi(x),其中Fi是个体适应度值,ΣFi(x)是所有个体适应度值的和。
4.交叉操作
随机选取两个个体,进行交换组合,把父代优秀基因传递给下一代,产生新个体。第k个染色体ak与第l个染色体al在j位进行交叉为:

其中,b是[0,1]区间上的随机数。
5.变异操作
以一定概率产生变异基因数,用随机方法从种群中选取个体进行变异生成更优个体。第i个个体第j个基因aij的变异操作为:
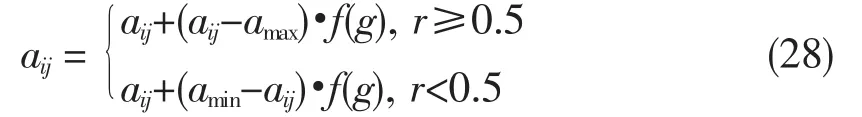
其中,amax为 aij的上限,amin为 aij的下限,f(g)=r2(1-g/Gmax)2,r2为随机数,g为当前迭代次数,Gmax为迭代次数的最大限度,r为[0,1]的随机数。
(二)模型算法改进的步骤和流程图
步骤1设置最初迭代次数t=1,种群规模popsize,交叉概率 Pc,变异概率Pm,最大迭代次数 Gmax。
步骤2 利用logistic映射生成初始种群,计算个体适应度,判断是否符合优化准则,若符合则输出最优个体及最优解,迭代结束;反之转步骤3。
步骤3 利用轮盘赌方式进行选择,选中适应度高的个体,淘汰适应度低的个体。
步骤4 按交叉概率方法,利用式(27)生成新个体。
步骤5 按变异概率方法,利用式(28)生成新个体。
步骤6 由交叉和变异生成新一代种群,返回步骤2,循环上述操作直至最终得到符合条件的最优个体为止。图1为可能性均值-下半方差-熵多期投资组合模型算法改进的具体操作流程图。

图1 可能性均值-下半方差-熵多期投资组合模型算法改进的流程图
四、可能性均值-下半方差-熵多期投资组合模型实证分析
为了验证模型(21)和模型(22)的实用性和可行性,从上海证券交易所中随机选取四只股票S1(海螺水泥600585)、S2(金地集团600383)、S3(上海汽车600104)、S4(三一重工600331),对2009年1月至2014年12月的月收益率的数据进行模拟投资。将整个投资过程分为三期,每一期结束时的收益作为下一期的初始财富继续进行投资,直至得到最终财富。四只股票在三个周期的收益率分布[14]如表1。
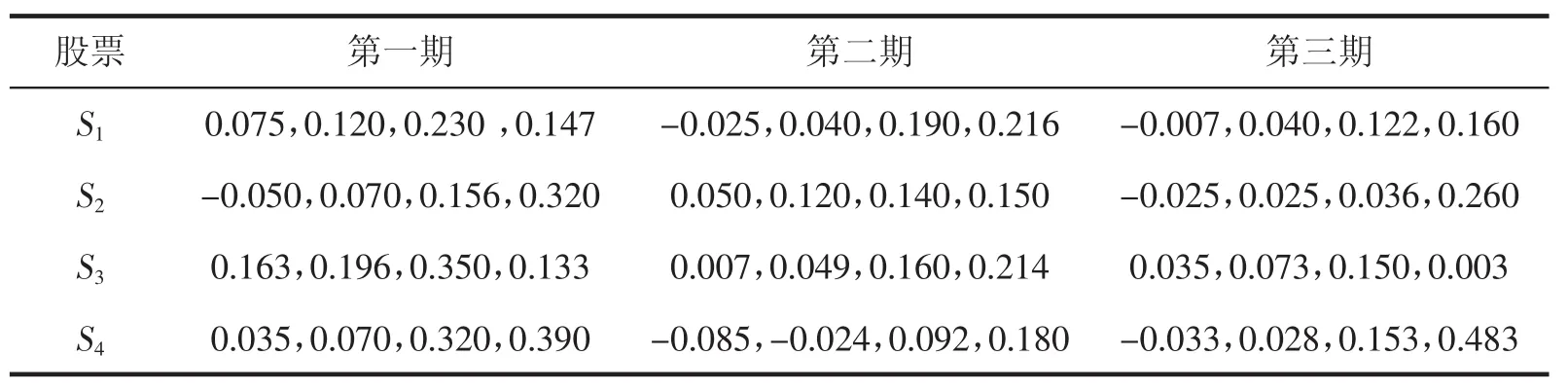
表1 三个周期股票收益率的可能性分布
参数设置:种群规模sizepop=30,交叉概率Pc=0.7,变异概率Pm=0.01,最大进化次数Gmax=500,最大投资数目限制k=4。假设每个阶段的资产交易费用是相同的,都为Cit=0.003,假设投资者初期所持有的财富W1=1万元,投资比例的下限、上限分别为lit=0.05,uit=0.2,罚因子L=108。无风险资产投资比例下限、借款利率、贷款利率分别为:xftl=0.5,rbt=0.017,rlt=0.009。
表1中收益率分布为梯形模糊数表示方法,如S1在第一期收益率可能性分布为(0.075,0.120,0.230,0.147),其中[0.075,0.120]为容许区间,0.230为该分布的左宽度,0.147为右宽度。
为了全面地了解投资者对风险的偏好程度,本文将风险态度划分为几个不同程度,并求出不同风险态度下投资者的投资组合策略如表2。

表2 不同风险态度时投资者的投资组合策略、收益及下半方差
由表2知,当风险态度k=0时,在第二期投资者增加投资第一、三、四只股票,减少投资第二只股票;而在第三期投资者增加投资第一、二只股票,不同程度地减少投资第三、四只股票的比例。可见投资者前期不看好第二只股票,其余都看好,后期只看好第一、二只股票,不太看好第三、四只股票。当风险态度k=0.2时,在第二期投资者增加投资第三、四只股票,减少投资第一、二只股票;在第三期投资者增加投资第一只股票,减少第二、三、四只股票的投资比例。可见投资者前期看好第三、四只股票,后期看好第一只股票,不太看好第二、三、四只股票。
由表2还知,当风险态度k=0.4时,在第二期投资者对四只股票均加大投资力度,在第三期投资者增加投资第三只股票,不同程度地减少第一、二、四只股票的投资比例。可见投资者前期对四只股票都看好,后期看好第三只股票,不看好第一、二、四只股票。当风险态度k=0.6时,在第二期投资者对四只股票均减少投资,而在第三期减少第一、二只股票的投资比例,增加投资第三、四只股票。可见投资者前期对四只股票均不看好,后期看好第三、四只股票,不看好第一、二只股票。当风险态度k=0.8时,在第二期投资者增加投资第一、三、四只股票,减少投资第二只股票;而在第三期减少第二、四只股票的投资比例,增加第一、三只股票的投资比例。可见投资者前期看好第一、三、四只股票,后期看好股票第一、三只股票,不看好股票二、四只股票。当风险态度k=1.0时,在第二期投资者增加投资第二、四只股票,减少投资第一、三只股票,而在第三期减少第二、三只股票的投资比例,增加投资第一、四只股票。可见投资者前期看好股票二、四只股票,不看好第一、三只股票,后期看好股票第一、四只股票,不看好第二、三股票。而且可以明确看到随着风险态度的逐渐增大,下半方差和熵值及收益都是逐渐增加的,进一步表明风险与收益并存。
不同风险态度下的函数值如图2所示。
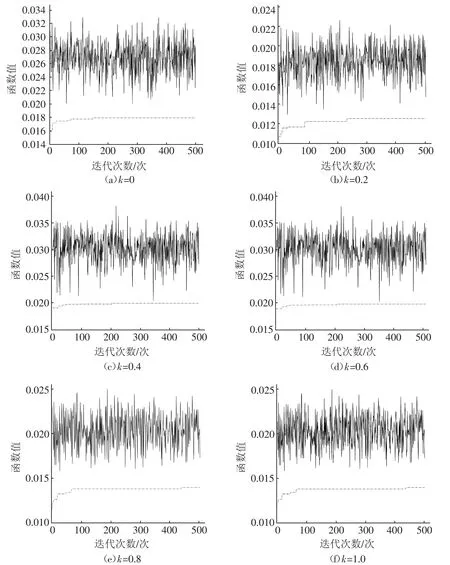
图2 不同风险态度下的函数值
图2为不同风险态度下函数值随迭代次数的变化。由图2可以看出,种群最优适应度值均以很快速度收敛并稳定。风险态度k=0时函数最优值在接近第150次迭代时趋于平稳,而风险态度k=0.2时最优值在第250次迭代之后趋于平稳,风险态度k=0.4时函数最优值在接近第200次迭代时趋于平稳,风险态度k=0.6时函数最优值在接近第300次迭代时趋于平稳,风险态度k=0.8和k=1.0时函数最优值均在接近第400次迭代时才趋于平稳。表明风险态度大时收益值波动较大,即追求风险的投资者需要承担更大的风险,且其收益值波动相较于规避风险者而言也是较大的。
由图3可以看出,随着风险态度适应值的增加,风险也随之增加。表明风险态度适应度值小时投资者厌恶风险,投资较为谨慎,风险适应度值大时投资者追求风险且希望得到较高的收益,所以投资行为也较为大胆。尤其k=0时风险值增大相较于其它是缓慢的,k=0.4,0.6,0.8时收益值随着下半方差的增大而增大,且变化较明显。k=1.0时随着风险值的增大,收益值不发生变化。表明高收益与高风险、低收益与低风险皆不可取,并告诫投资者需谨慎投资。
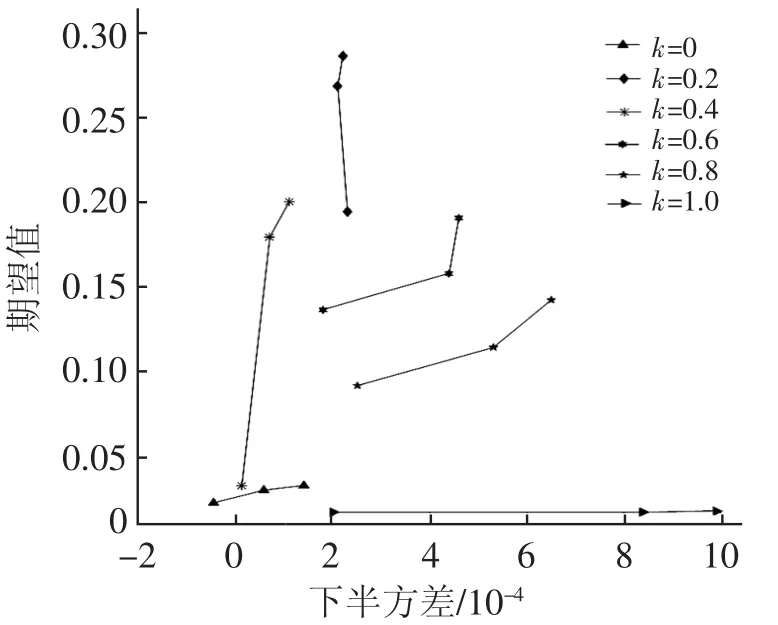
图3 不同风险态度下的有效前沿对比
图4为不同风险态度下三个不同时期下半方差与收益的变化。
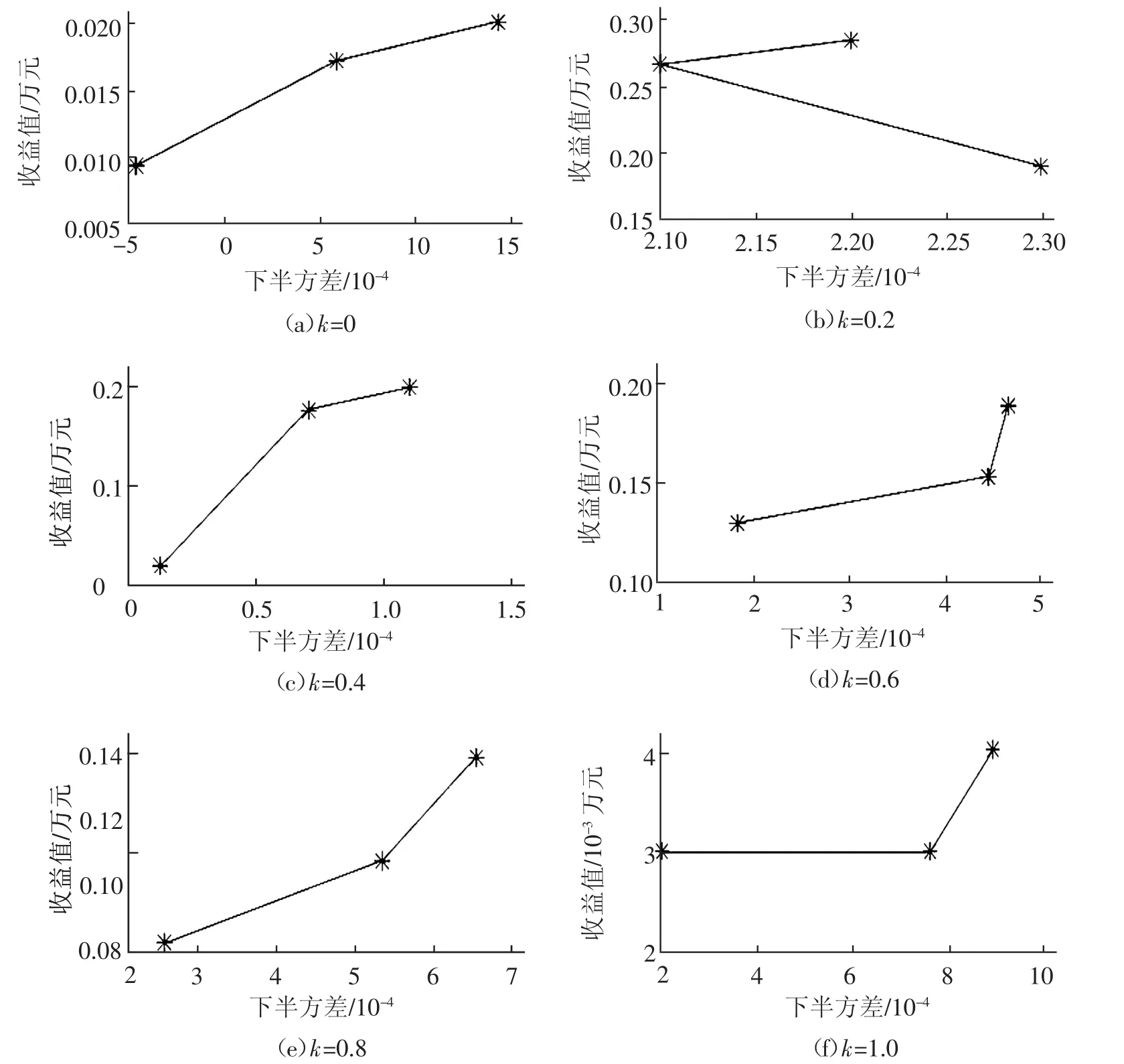
图4 不同风险态度下收益与下半方差的关系
由图4可以看出,k=0时前期收益增速快,后期较慢。k=0.2时前期收益下降快,后期较慢。k=0.4时前期收益增速快,后期较慢。k=0.6时前期收益增速慢,后期较快。k=0.8时前期收益增速慢,后期较快。k=1.0时前期收益不变,后期收益增速变快。即随着下半方差的增大,收益值也随之增加,但也会存在高风险低收益的情况,即收益与风险不成正比的情况,本研究结果表明在任何时期投资都存在风险,投资者需谨慎投资。
五、结语
在日益复杂的金融市场中,随着经济的不断发展,人们对资产的处置方式越来越多样化,更多人选择通过投资达到财富的再提升。经过多位学者对该问题的研究,其重点逐渐集中在对构建模型的改进和求解方法的创新上,这两点是投资组合研究的重点,同时也是热点。本文在文献[11]的基础上同时考虑下半方差及交易费用等多种摩擦因素,引入收益权重建立可能性均值-下半方差-熵多期投资组合优化模型。相较于文献[11]构建的均值-熵模型只考虑到宏观层面风险进行风险度量存在的盲点和片面性,本文所建模型可以用熵和下半方差对风险进行度量,能够全面考虑到宏观和微观两个层面的风险,而且能在确保投资者获取超额收益的同时更大程度地规避风险。由于本文所建模型是带有不等式约束的NP难问题,所以用外点罚函数法对模型进行无约束处理。在标准遗传算法的基础上引入混沌映射改变种群提取过程,其目的是提高种群多样性和寻优能力。随机从上证50中选取四只股票进行仿真实验,分析了不同风险态度下的投资组合方案、函数值随迭代次数变化、收益值随下半方差改变而产生的波动和有效前沿对比。数值结果表明本文所建模型是可行合理的,比文献[11]中的模型在获取收益和控制风险方面考虑得更为周到,有帮助持有杠杆资金的投资者有效控制风险的作用。同时也说明了改进的算法在求解该类模型方面效果较好,是有效可行的,即本文所建模型可以应用到实际的投资组合中,帮助投资者规避风险并获取超额收益。但也表明高风险投资最终不一定就能获得高收益,依此告诫投资者不能一味地追求风险,在投资时应该充分结合个人风险态度及证券市场实情进行全面考虑谨慎投资。

