踩点作答 步步为营
文/王 进
方程(组)与不等式(组)的解答不仅考查我们的计算能力,更关注我们的解题过程。在答题时,很多同学明明会做,却在步骤上频频失分。下面老师将围绕本块知识的规范书写格式进行讲解,供同学们复习时参考。

一、二元一次方程组
例1(2021·江苏扬州)已知方程组的解也是关于x,y的方程ax+y=4的一个解,求a的值。
解法1(代入消元法):
把②代入①,得2(y-1)+y=7,
解得y=3。
把y=3代入②,得x=2。
∴原方程组的解为
解法2(加减消元法):
②×2,得2x=2y-2,③
①-③,得y=9-2y,
解得y=3。
把y=3代入②,得x=2。
∴原方程组的解为
二、一元一次不等式组
【易扣分点】①计算过程出错;②使用代入消元法时,漏加括号;③使用加减消元法时,常数项漏乘扩大或缩小的倍数;④最后没有用大括号写成方程组的解;⑤只求出方程组的解,忽略了求a的值。
【方法指导】解二元一次方程组时,若方程组中未知数的系数为分数或小数,我们一般先将其化为整数,再观察系数的特征选择代入消元法或加减消元法,最后转化为一元一次方程进行求解。
例2(2021·江苏连云港)解不等式组:
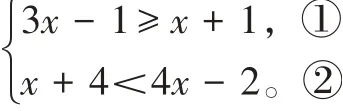
解:由①,得2x≥2,x≥1。
由②,得-3x<-6,x>2。
∴原不等式组的解集为x>2。
【易扣分点】①缺少过程性步骤;②不等式的两边都乘同一个负数时,不等号的方向没有改变;③最后漏写原不等式组的解集。
【方法指导】在解不等式组时,先分别求出每个不等式的解集,尤其是遇到复杂不等式时,要一步一个脚印,切忌跳步骤书写。此外,在利用不等式的性质时,要注意,不等式两边都乘同一个负数时,不等号的方向要改变。最后,我们不要漏写不等式组的解集。
三、分式方程
例3(2021·江苏南京)解方程
解:方程两边同乘(x+1)(x-1),得
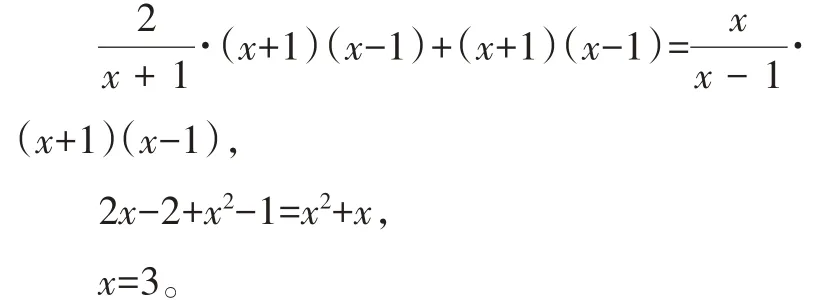
经检验,x=3是原方程的解。
∴原方程的解为x=3。
【易扣分点】①常数项漏乘最简公分母;②漏写检验根的步骤;③漏写总结语——原方程的解。
【方法指导】我们在解分式方程时,首先,应观察方程,找到最简公分母;其次,用方程的每一项与最简公分母相乘,将分式方程转化为整式方程,注意常数项不要漏乘,去掉分数线时要加括号;再次,解完整式方程后一定要检验,避免整式方程的解代入分式后使得分母为零,出现增根;最后,总结原方程的解。
四、一元二次方程
例4(2021·江苏无锡)解方程:(x+1)2-4=0。
解法1(直接开平方法):(x+1)2=4,
x+1=±2,
∴x1=1或x2=-3。
解法2(公式法):x2+2x+1-4=0,
x2+2x-3=0。
∵a=1,b=2,c=-3,
∴b2-4ac=22-4×1×(-3)=16>0,
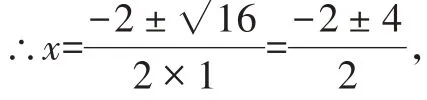
∴x1=1或x2=-3。
解法3(因式分解法):x2+2x+1-4=0,
x2+2x-3=0。
(x-1)(x+3)=0,
∴x-1=0或x+3=0,
∴x1=1或x2=-3。
本题还可用平方差公式求解:
由(x+1)2-4=0,得
(x+1+2)(x+1-2)=0,
(x+3)(x-1)=0,
∴x1=1或x2=-3。
【易扣分点】①缺少过程性步骤;②根的判别式记错;③计算错误;④结果未写成“x1=……或x2=……”的形式。
【方法指导】我们在解一元二次方程时,首先,应认真审题,看题目中是否规定了用哪种方法;其次,观察方程特征,选择最合适或者最熟悉的方法;最后,结果写成“x1=……或x2=……”的形式。采用配方法时,应先将二次项系数化为1,再将常数项移到等式的右边,接着等式两边同时加上一次项系数一半的平方。采用公式法时,应先判断根的判别式是否大于或等于零,再利用求根公式算出结果,结果须化成最简形式。记住,公式法是最万能的解法,适用于所有情况。采用因式分解法时,方程的右边必须化为零,左边必须化为两个整式乘积的形式,常用提取公因式或者公式法来分解因式。

