夯实基础 感悟解法——盘点“二次根式”的解法

文／赵倩倩

二次根式是初中数学“数与式”的主要内容之一，也是中考考查的重点。因此，同学们除了要牢固掌握基础知识、基本技能和基本思想方法外，还要能正确熟练地运用相关知识解决各类问题。

一、二次根式的概念

例1若有意义，则x的取值范围是_____。

【分析】本题考查二次根式a有意义的条件：被开方数a≥0。

解：根据题意，得x-1≥0，解得x≥1。

故答案为x≥1。

【点评】本题考查了二次根式有意义的条件，利用被开方数是非负数得出不等式是解题关键。

例2下列各组二次根式中，化简后是同类二次根式的是（ ）。

【分析】本题考查同类二次根式的概念，应先将各选项化成最简二次根式，再根据被开方数是否相同进行判断即可。

解：A选项，，和不是同类二次根式，本选项不合题意；

故选D。

【点评】本题考查了同类二次根式的概念，解题的关键在于熟练掌握二次根式的化简及同类二次根式的概念。

二、二次根式的性质

例3已知：，则

【分析】本题考查二次根式的性质，平方差公式（a+b）（a-b）=a2-b2以及零指数幂、负整数指数幂的计算。先计算出a、b的值，然后代入所求式子即可求得相应的值。

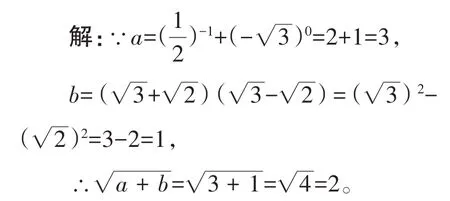
故答案为2。

【点评】本题考查了二次根式的化简求值、平方差公式、零指数幂、负整数指数幂，解题的关键是明确它们各自的计算方法。

例42、5、m是某三角形三边的长，则等于（ ）。

A.2m-10 B.10-2mC.10 D.4

【分析】直接利用三角形三边关系得出m的取值范围，再利用二次根式的性质化 简 得 出答案。

解：∵2、5、m是某三角形三边的长，

∴5-2＜m＜5+2，

故3＜m＜7，

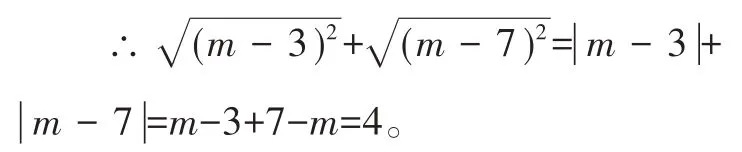
故选D。

【点评】本题主要考查了三角形三边关系以及二次根式的化简，正确化简二次根式是解题关键。

三、二次根式的计算

例5计算的结果是_____。

【分析】本题考查同类二次根式的合并以及二次根式的乘法运算。二次根式的乘法运算法则：0，b≥0）。

解：原式

【点评】本题主要考查了二次根式的混合运算，熟练掌握二次根式的乘法运算法则是解题的关键。

例6计算的结果是__。

【分析】本题考查同类二次根式的合并以及二次根式的除法运算。二次根式的除法运算法则b＞0）。

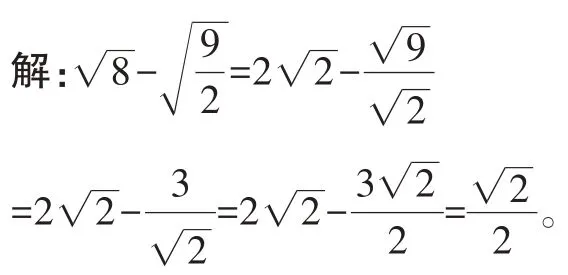
【点评】本题主要考查了二次根式的混合运算，熟练掌握二次根式的除法运算法则是解题的关键。