对“抽象”的全景式解读——以《认识三角形》一课的教学为例

江 苏 南 京 赫 贤 学 校（210000）

北京全景化教育科技发展中心（100000） 张宏伟（特级教师）

一、追根溯源

（一）对“抽象”中文概念的追溯

1.抽

（1）字源演变

（2）说文解字

全景式数学教育团队认为，在数学教学和数学研究中，“抽象”中的“抽”有从现象、对象、生活、素材中抽出、抽取之意。

2.象

（1）字源演变

（2）说文解字

《说文解字》中，“象”的本义是大象，一种哺乳动物，后来引申义为形状、样子。

《韩非子·解老篇》：“人希见生象也，而得死象之骨，按其图以想其生也，故诸人之所以意想者，皆谓之象也。”

《易·系辞》：“象也者，像此者也。”

《疏》：“言象此物之形状也。”

综上所述并对比之，全景式数学教育团队认为，在数学教学中，“抽象”中的“象”应指认识对象的形状、属性、本质、特征等，相当于柏拉图中的理想型。

（二）“抽象”在《汉语大辞典》和《辞海》中的解释

1.在《汉语大辞典》中的解释

（1）从许多事物中，舍弃个别的、非本质的属性，抽出共同的、质的属性，是形成概念的必要手段。

（2）不能具体经验到的，笼统的，空洞的。

2.在《辞海》中的解释

（1）同“具体”相对，指事物某一方面的本质规定在思维中的反应。

（2）指思维活动的一种特性，即在思想中抽取事物的本质属性，撇开非本质属性。

（3）指形而上学的思维特点，亦称空洞的抽象。

（三）全景式数学教育团队的理解

结合对“抽象”中文概念的追溯，我们认为数学中的“抽象”是从具体的事物中去除外在的、个别的、非本质的东西，提炼（即“抽”）出这类事物共同的、本质的属性，如形状、样子、特征、规律、关系等，并上升为理性的、理想型的“像”的思维过程。同时，抽象出的结果是对客观事物的模拟和再现，并要泛化、归回、概括、审视到所有此类的具体事物中，即“而得死象之骨，按其图以想其生也”，我们把这个过程定义为“回象”。因此，全景式数学教育团队认为“抽象”应该是一个从具体到抽象再到具体的过程，而不仅仅是从具体到抽象的过程。

二、教育专家和一些经典论著中的阐述

许多数学家和数学教育研究者对“抽象”一词有过相关的描述。如史宁中教授认为：“数学教学的最终目标是要让学习者会用数学的眼光观察现实世界……而数学的眼光就是抽象……最初的抽象是基于直观的。对于数学，抽象主要包括两个方面的内容：数量与数量关系，图形与图形关系。这就意味着，数学的抽象不仅仅要抽象出数学所要研究的对象，还要抽象出这些研究对象之间的关系。与研究对象的存在性相比，研究对象之间的关系更为本质。”同时，史宁中教授还将抽象的深度大体分为三个层次：“一是简约阶段，即把握事物的本质，把繁杂问题简单化、条理化，能够清晰地表达；二是符号阶段，即去掉具体的内容，利用概念、图形、符号、关系表述，包括已经简约化了的事物在内的一类事物；三是普适阶段，即通过假设和推理建立法则、模式或者模型，并能够在一般意义上解释具体事物。”王永春教授也指出：“数学抽象是对现实世界具有数量关系和空间形式的真实材料进行加工、提炼出共同的本质属性，用数学语言表达进而形成数学理论的过程。”

三、课程标准中的解释和相关论述

《义务教育数学课程标准（2011年版）》在前言中指出：“数学作为对于客观现象抽象概括而逐渐形成的科学语言与工具，不仅是自然科学和技术科学的基础，而且在人文科学与社会科学中发挥着越来越大的作用。”数学学习能培养学生的抽象思维和推理能力，所以教师预设教学时要处理好直观与抽象的关系，教学设计要在呈现作为知识与技能的数学结果的同时，重视学生已有的知识经验，使学生经历从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。

在数学课程总目标中，知识与技能方面提出要经历数与代数的抽象、运算与建模等过程，掌握数与代数的基础知识和基本学习技能；要经历图形的抽象、分类、性质探讨、运动、位置确定等过程，掌握图形与几何的基础知识和基本学习技能。对于学生的数学思考方面，则要求建立数感、符号意识和空间观念，初步形成几何直观能力和运算能力，发展形象思维与抽象思维。

在学段目标中，每一学段都有不同层次的要求。在知识与技能方面，第一学段要经历从日常生活中抽象出数的过程，理解万以内数的意义，初步认识分数和小数，同时经历从实际物体中抽象出简单几何体和平面图形的过程，了解一些简单几何体和常见的平面图形；第二学段要体验从具体情境中抽象出数的过程，认识万以上的数；第三学段要体验从具体情境中抽象出数学符号的过程，理解有理数、实数、代数式、方程、不等式、函数。数学思考方面，第一学段要从物体中抽象出几何图形，在想象图形的运动和位置的过程中发展空间观念。情感态度方面，第三学段要在运用数学表述和解决问题的过程中，认识数学具有抽象、严谨和应用广泛等特点，体会数学的价值。

另外，课程标准在课程资源开发与利用的建议中，要求使用有效的数学软件绘制图形，呈现抽象对象的直观背景，加深学生对所学数学知识的理解。

四、抽象的基本流程

那么，教师如何实施数学抽象教学呢？基于对“抽象”这个概念的分析和理解，我们认为至少应该经历以下四个步骤：第一步，选材，即从复杂的环境中排除非典型对象，抽取和确定典型的研究对象；第二步，生象，即集合所有的典型对象，通过对比、观察、想象，抽取出共同的属性、关系、形式或数量关系，也就是理想型；第三步，概念化，即利用概念、符号、图形、关系式等构建图式、模型，形成概念；第四步，回象，指理解概念之后的综合运用、拓展延伸，即“而得死象之骨，按其图以想其生也”。

五、教学案例

在此呈现我们全景式数学教育团队研究的一个教学案例——《认识三角形》，供大家参考。

课前思考：

《认识三角形》是人教版数学四年级下册第五单元的内容，在第一学段中，学生已经直观、初步认识了三角形和其他一些简单的平面图形，具备了直观认识三角形和从平面图形中寻找三角形的能力。

三角形是学生在日常生活中见得最多的平面图形，如何从常见的三角形物体中抽象出三角形，再把三角形知识应用到现实生活中，引导学生全面深入地研究三角形呢？基于全景式数学教育所倡导的“全景视野下的长线浸润式教学”，把本节课分为前期整体浪漫浸润和课中专项研究两个阶段，这样不仅能拓展学生的知识视野，而且可以丰富学生的学习方式，改变学生对数学学习单一、刻板的印象。

教学目标：

1.利用生活经验，通过观察、操作、实验等活动，认识三角形和三角形的特征，知道三角形高和底的含义，会在三角形内画高。

2.在认识三角形特征的活动中，学习认识多边形特征的基本方法，培养观察、比较、抽象、概括等能力。

3.体会数学与生活之间的密切联系，并在活动中进一步激发学生学习图形的兴趣。

教学重点：

认识三角形，掌握三角形的基本特征。教学难点：

三角形的高及画法。

教学过程：

（一）前期开启整体浪漫浸润

为了丰富学生关于三角形的积累，教学初就启动前期整体浪漫浸润阶段，即让学生有意识、有目的地搜集生活中的三角形，使学生从整体上感知和了解三角形，积累丰富的数学活动经验。然后将搜集到的三角形物体摆放在教室里，将无法搬移的实物拍成照片，打印出来贴在教室的墙壁上，让学生思考它们在生活中的作用并记录下来。

【设计意图：引导学生寻找生活中的三角形，使学生从整体上感知和了解三角形，为学生全面认识三角形、初步感受三角形在现实生活中的应用，以及进一步深入研究三角形的特征奠定基础。】

（二）课中专项研究

1.回顾选材

把学生搜集到的三角形实物摆放在教室里，并将学生搜集到的有关三角形的资料制作成短片在课前播放，进一步激发学生研究三角形的兴趣。

2.生象

师：同学们在之前的自主学习中，寻找到许多三角形的实物，现在请闭上眼睛想一想，三角形是什么样子的？同时把它画下来。（展示学生画的三角形）你们是怎么画的？

生1：房子的屋顶呈三角形，我把它的轮廓画出来了。

师：也就是说，在画三角形的时候，不考虑物体的颜色、花纹、材质，只画出物体的轮廓。

【设计意图：重视学生的想象和已有的认知经验，进一步引导学生经历从具体的三角形实物中逐步抽象出三角形的过程。】

3.概念化

活动A：抽取特征。

师：同学们画的三角形都不一样，那它们有什么共同的特征？

生2：都有三个角，三条边。

生3：还有三个顶点。

师：现在请同学们找一找自己画的三角形的边、角、顶点，并试着标注出它们。（学生操作略）

师：同学们，通过画三角形以及探究三角形的特征，你们觉得什么样的图形是三角形？

生4：有三个角、三条边、三个顶点的图形是三角形。

活动B：用反例辩证。

师：大家同意吗？

生5：我觉得不一定。你们看我画的图（如右图），虽然也有三条边、三个角、三个顶点，但是有一条边是弯曲的，它就不是三角形。

师：那三角形的三条边必须符合什么条件？

生6：应该都是直的。

生7：应该是三条线段。

师：那由三条线段组成的图形一定是三角形吗？（出示右图）请同学们看看这两个图形。

生8：它们都不是三角形。第一个图形虽有三条边、三个角，但这三条边没有连接起来；第二个图形虽然有三条边，但有缺口，没有封闭。

师：你能用自己的话概括三角形的定义吗？

生9：由三条线段组成的封闭图形是三角形。

生10：由三条线段围成的图形叫作三角形。

师：你能结合刚才画的图形解释一下什么是“围成”吗？

生10：三角形有三条线段，每两条线段的端点连接在一起，这就是“围成”，“围成”一个封闭的图形。

活动C：形成规范、标准的概念。

师：由三条线段围成（每两条线段的端点相连）的图形叫做三角形。

【设计意图：三角形的定义较难用学生易理解的数学语言进行表述，通过对三角形特征的辨析，引发学生对三角形定义判断依据的反思。】

活动D：用字母表示三角形。

师：为了方便，我们还可以用字母来表示三角形。（在三角形的顶点分别标上A、B、C，读作三角形ABC，记作△ABC）

4.回象

师：我们认识了三角形的特征，现在请同学们观察这些实物和图片，从中找出三角形并说出判断的理由和依据。（学生寻找三角形并进行判断说明）

【设计意图：再一次引导学生回归到具体实物中，完整地经历概念抽象的过程——从具体到抽象再到具体，即回象。】

5.认识三角形的高

（1）选材与生象

师：同学们，我们前面学过的平行四边形有底和高，那么今天学习的三角形有底和高吗？

生：有。

师：什么是三角形的高？什么是三角形的底？请同学们带着问题自学课本第61页的内容，小组内交流讨论。（学生汇报自学情况）

（2）概念化

师：从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段是三角形的高，这条对边是三角形的底。

师：同学们知道了什么是高，那怎样画三角形的高呢？请试着画一画，并和同桌交流自己的画法。（学生反馈，交流画法）

生11：我用三角尺的直角来画的。

生12：我将三角尺的一条直角边和三角形的底边重合，然后沿着底边移动，当另一直角边过三角形的顶点时，从顶点出发向底边画一条垂线，这条垂线就是三角形的高。

师：我们认识了三角形的高，谁来说一说锐角三角形可以画几条高？

生：三条。

师：请把锐角三角形的另外两条高也画出来。（学生操作后展示作品，交流反馈）

师：锐角三角形能画出三条高，那有一个角是直角的三角形和有一个角是钝角的三角形是不是也能画出三条高呢？请同学们在练习本上试一试，并在小组内交流。

生13：我们选择有一个角是直角的三角形，发现只需要画一条高，另外两条高不用画，因为这两条高是三角形的两条直角边。

师：他说得对吗？你能在黑板上用直角三角尺指一指这个直角三角形的高和底吗？（学生边解释，边指出直角三角形的另外两条高）

生14：（出示右图）我们小组研究了有一个角是钝角的三角形，只能画出一条高。

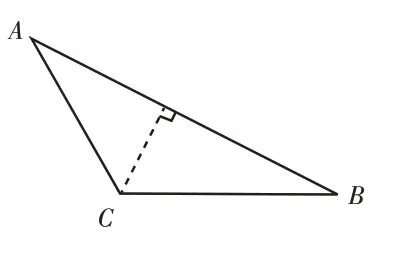
师：他们研究的这个三角形有点特殊，其中有一个角是钝角，于是他们从钝角的顶点C向对边AB作了一条垂线，找到了一条高。但是，这个三角形只能画一条高吗？

生15：可以把另外两条边延长，就可以画出另外两条高了，且这两条高都在三角形的外面。

（教师组织学生交流讨论把钝角三角形中两个锐角作为顶点作高的过程，并比较这个高与前面的高的不同，完善学生对高的理解和认识，这个过程即为“全象”）

【设计意图：引导学生在尝试画高的过程中认识三角形的底和高，学会画三角形的高，培养学生的观察和动手操作能力。】

（3）回象

教师呈现生活中各种有高或者类似高的三角形物体，让学生根据高的概念判断说明哪些是高或者接近高，哪些不是高。

6.拓展延伸

师：今天我们学习的三角形都是平面三角形，生活中也有不少球面三角形（多媒体呈现下图），即球面上由三条弧线围成的三角形就是球面三角形。

【设计意图：让学生体会球面三角形在生活中的应用，拓展和丰富学生对三角形的认识。】

……

小学数学教学中还有许多核心概念，如概括、模型、迁移、推理等，教师对这些概念本身的内涵理解得越深入、越全面，也就越能有效地利用它们指导自己的课程设计和教学实施，从而取得好的教学效果。全景式数学教育团队筛选出20个这样的核心概念进行全面、深入、立体的解读，并针对每个核心概念提供了相应的教学流程和典型案例（详见《小学数学20个核心概念的全景解读》一书，即将出版），希望能给小学数学教师带来一些可行的借鉴。