考虑界面滑移效应的钢-混凝土组合梁-新型非线性纤维梁单元模型
宋福春,苏洪业,刘 帅
(沈阳建筑大学交通工程学院,辽宁 沈阳 110168)
钢-混凝土组合梁作为一种典型的组合结构形式,充分考虑了钢材和混凝土材料的力学特点,具有恒载小、延性高、施工速度快等显著特点,在现代化桥梁建造中表现出极具竞争力的技术经济优势[1]。近年来,钢-混凝土组合梁在我国桥梁建造中的应用日益广泛,对钢-混凝土组合梁力学性能的研究也得到越来越多的关注[2]。
钢梁与混凝土板界面的抗剪连接键是影响钢-混凝土组合梁组合效应的关键因素[3-4]。设计规范根据剪力键连接程度的不同,将其划分为部分抗剪连接和完全抗剪连接,并指出对部分抗剪连接键应考虑其对结构刚度和承载力的影响[5]。同时,即便是完全抗剪连接设计的组合梁结构,由于栓钉等柔性连接键的变形,界面滑移变形总是不可避免地要发生,界面完全连接仅是一种理想状态[6]。
鉴于此,不少研究学者开展了大量的试验研究测试了界面连接程度对组合梁变形及承载力的影响。张林彦[7]通过缩尺试验梁测试得到,抗剪连接键数目降低62.5%后,结构抗弯承载力降低了约27%。吴霖[8]试验测试了栓钉锈蚀率对组合梁力学性能的影响,测试结果表明,栓钉锈蚀率达到25.86%后,结构抗弯承载力降低5.16%。Y.Xing等[9]开展的试验研究表明界面抗剪连接程度降低26%后试验梁变形增加了12.7%。B.Wang等[10]对4片组合梁的测试结果表明,剪力键连接刚度降低一半,组合梁抗弯承载力降低13.7%。
在理论分析模型研究方面,当前考虑钢-混组合梁界面滑移效应的分析模型主要包括三类:实体有限元模型[11]、双层梁单元模型[12]和单梁模型[13]。实体分析模型主要采用壳或实体单元来分别模拟钢梁及混凝土板,在界面处采用非线性弹簧单元或者实体模拟栓钉来考虑界面作用;其特点是模型适用性广,但同时也存在求解成本高计算效率低的技术难题。双层梁单元模型则是在同一位置采用梁单元将钢梁及混凝土板分别模拟,单元的位置重合,节点间采用弹簧单元模拟界面滑移;单梁模型方法将钢梁与混凝土作为一个整体梁单元来模拟,并将界面滑移作为一种变形模式引入。目前计算软件中尚无这种减小计算量进行非线性分析的梁单元类型,相关学者的研究均采用自编程序进行结构计算,且仅可进行线弹性分析。钢-混组合梁在全寿命服役期内,不可避免地存在混凝土板开裂、压碎、钢梁屈服等非线性行为,单元刚度矩阵不再是常数,而是随着承载状态的不同不断变化,目前的单梁模型研究尚无法适用。
基于上述分析,笔者借助于纤维梁单元模型在结构非线性分析方面的优势,在传统纤维梁单元理论的基础上,引入界面滑移变形模式,建立考虑钢-混组合梁界面滑移的非线性单梁理论模型,实现了考虑材料非线性行为后的单元刚度及抗力迭代计算。笔者基于所建立的理论模型,在OpenSees软件进行新单元的二次开发,通过对典型试验梁的分析对比,验证了所建立理论模型及开发计算程序的有效性。研究表明:笔者所建立的理论模型拓展了考虑滑移效应的单梁模型对钢-混组合梁非线性行为分析的适用性。
1 单元理论模型及二次开发
1.1 单元定义
纤维梁单元模型是一种非线性梁单元类型,它采用了梁单元平截面假定的基本假设来描述单元变形,但在截面上采用离散的纤维划分来分别考虑不同位置纤维的刚度及抗力,再通过纤维求和的方式计算截面刚度和抗力[14]。笔者在传统纤维梁单元理论的基础上,引入钢梁与混凝土板间滑移变形模式,推导建立新的可考虑界面滑移的非线性纤维梁单元模型。
新建梁单元如图1(a)所示。2节点8自由度平面梁单元,单元长度为L,截面纤维划分如图1(b)所示,单元变形模式如图1(c)所示。


图1 考虑滑移效应的纤维梁单元示意图Fig.1 Schematic diagram of fiber beam element considering interface slip effect
1.2 单元列式推导
局部坐标系下单元节点位移向量如式(1)所示,单元抗力向量如式(2)所示。uc及us分别表示混凝土板和钢梁的轴向位移;v及θ分别表示节点竖向位移和转角;Fc及Fs分别表示混凝土板和钢梁的轴力;Q和M分别表示单元内剪力及弯矩;下标i和j分别表示节点编号。
u=[uciusiviθiucjusjvjθj]T.
(1)
F=[FciFsiQiMiFcjFsjQjMj]T.
(2)
(3)

Pu.
(4)
ub(x)=[uc(x)us(x)θ(x)]T=
(5)
根据几何方程,可得到坐标x位置截面变形如式(6)所示,其中εc(x),εs(x)和φ(x)分别表示混凝土板、钢梁轴向应变和截面曲率;ucs(x)为坐标x截面处混凝土板与钢梁间的相对滑移。
us(x)=[εc(x)εs(x)φ(x)ucs(x)]T=
(6)
根据如图1所示截面变形模式,坐标x位置截面(y,z)坐标处纤维的轴向应变如式(7)所示,界面滑移如式(8)所示。其中,ψc和ψs分别为混凝土板及钢梁分区标志参数,当纤维(y,z)坐标位于混凝土板区域时,ψc=1,ψs=0;否则,ψc=0,ψs=1。
ε=[ψc(y,z)ψs(y,z) -y0]us(x)=
Q(y,z)us(x).
(7)
ucs(x)=[0 0 0 1]us(x)=Rus(x).
(8)
由式(7)中的纤维应变,可根据纤维单轴本构关系得到纤维的应力σ和切线模量E;同样可由式(8)中的界面相对滑移ucs(x),根据界面滑移本构曲线得到界面相互作用力fs和界面切线刚度ρs;将其表示为增量形式如式(9)~(10)所示。
Δσ=EΔε.
(9)
Δfs=ρsΔucs.
(10)
当单元发生Δu位移增量时,综合式(4)~(10),可将单元内势能表示为式(11)所示。Fe为单元外力增量;Ω,A及l分别表示对单元内、截面及单元长度方向的积分域。
PΔu-ΔuTFe.
(11)
根据势能变分原理,可推导出单元标准列式如式(12)所示;其中K为单元切线刚度矩阵,ks(x)为坐标x位置的截面刚度矩阵。类似地,采用虚功原理也可容易推导单元节点抗力向量F如式(15)所示,截面抗力向量rs(x)如式(16)所示。
KΔu=Fe.
(12)
(13)
(14)
(15)
(16)
式(13)及式(15)中单元刚度矩阵和抗力向量沿单元长度方向的积分可采用Gauss-Lobatto数值积分方法计算;式(14)及式(16)中截面刚度矩阵及抗力向量的积分则基于离散纤维的思想将截面积分转换为各离散纤维的刚度和抗力代数和的形式。截面刚度矩阵和抗力向量的展开形式分别如式(17)及式(18)所示,其中n表示为截面上离散纤维的数目,变量下标k表示编号为k的纤维对应的参数。
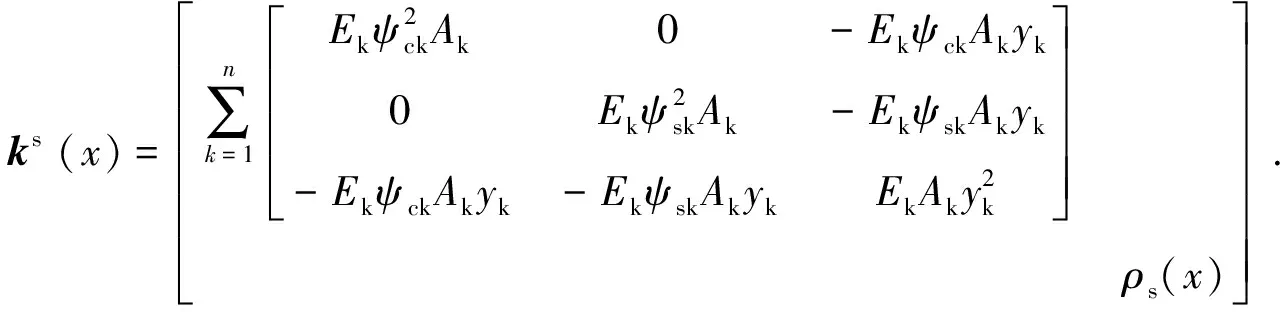
(17)

-σkAkyk]fs].
(18)
1.3 基于OpenSees软件的单元二次开发
OpenSees软件是一款开源的用于土木工程结构非线性分析的计算程序。目前,OpenSees软件中的传统纤维梁单元是基于平截面假定建立的,无法考虑钢-混组合梁界面的滑移效应。笔者在OpenSees开源程序架构的基础上,将上述推导建立的理论模型在OpenSees程序中进行了集成开发,形成了适用于钢-混组合梁滑移效应分析的新的单元类型。
1.3.1 迭代程序
在钢-混凝土组合梁结构分析中,将结构划分为若干个新单元,装配形成结构整体模型。采用完全牛顿迭代法对结构非线性效应进行计算分析,在每一步迭代计算中,根据承载状态的不同,依次对各纤维、积分点截面、单元和整体结构的刚度矩阵和抗力向量进行迭代更新,根据收敛准则对计算收敛性进行评判。
1.3.2 单元开发程序架构
采用C++设计语言在OpenSees源码中对新单元进行集成开发。依次开发了单元类、截面类、坐标转换类,整体单元开发架构及其与源程序对象的继承关系如图2所示。各纤维的材料本构和界面滑移本构关系可以利用OpenSees软件中丰富的非线性材料本构关系库进行模拟。

图2 单元开发架构Fig.2 Framework of developed element in OpenSees
1.4 材料本构关系
1.4.1 钢梁及钢筋材料
钢梁及钢筋材料均采用OpenSees软件中Steel01材料按照线性强化弹塑性材料进行模拟,如图3(a)所示。图中,ε为应变;σ为应力;fy为屈服强度;εy为屈服应变;Es为弹性模量;b为屈服后强化模量系数,可取0.005。
1.4.2 混凝土材料
混凝土采用OpenSees软件中考虑混凝土抗拉作用的Concrete02材料进行模拟[15],如图3(b)所示。图中,εt0和εt0分别表示峰值拉应变和峰值拉应力;εc0和εc0分别表示峰值压应变和峰值压应力;εcu和εtu分别表示极限压应变和极限拉应变;ft和fc分别表示混凝土抗拉强度和抗压强度;Ec表示混凝土切线模量。

图3 材料及界面本构关系Fig.3 Constitutive relations
1.4.3 界面滑移本构关系
混凝土板-钢梁的界面滑移关系采用J.G.Ollgaard提出的栓钉模型,如式(19)所示。其中,fs为界面剪力;ucs为界面滑移;n和m为常数;未对抗剪连接键进行滑移试验时刻按照经验取值m=0.4、n=0.7,Vu为单个栓钉的极限承载力,按式(20)计算;fu为栓钉极限抗拉强度;Aus为栓钉截面积;Ec为混凝土弹性模量。可采用OpenSees软件中的分段弹塑性本构MultiLinear来模拟。
fs=Vu(1-e-nucs)m.
(19)
(20)
2 模型验证及应用
笔者利用所建立的单元理论模型和开发的计算程序,分别对弹性及弹塑性加载下试验梁进行模拟分析验证。
2.1 正弯矩加载试验梁分析验证
文献[7]开展了钢-混组合梁的滑移效应对结构变形及承载力的影响试验,选取其中一组3片正弯矩加载试验梁作为分析案例进行对比验证。3片试验梁的设计参数基本一致,栓钉间距有所不同:SCB-1梁为100 mm,SCB-2为150 mm,SCB-3为285 mm。由材性试验测得试验梁所用混凝土抗压强度为33.67 MPa,弹性模量为3.35×104MPa。
计算3片试验梁单位长度的抗剪连接切线刚度ρs分别为10 609 MPa、7 073 MPa、3 722 MPa。
图4所示分别对四点加载和均布加载情况下,与文献[7]的对比结果界面滑移变形沿梁长方向的分布情况,横坐标为自梁端部至跨中截面的位置坐标。结果表明文中模型计算结果与解析解基本吻合,界面滑移的分布规律受加载类型的影响有所不同。

图4 弹性加载工况下界面滑移变形Fig.4 Interface slip of test beams under elastic loading
3片试验梁弹塑性加载全过程的荷载位移曲线分析结果与试验结果的对比情况如图5所示,表1及表2分别为结构变形和承载力计算结果与试验结果的对比,其中,对比值=(计算值-试验值)/试验值。
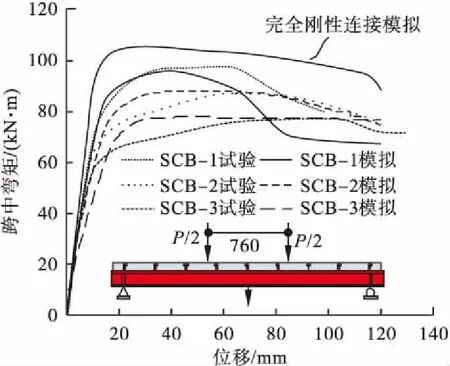
图5 正弯矩加载试验梁荷载位移曲线Fig.5 Load-displacement curves of test beams under positive moment loading

表1 试验梁变形计算结果对比Table 1 Comparisons between calculation and test results of structural deformation

表2 试验梁抗弯承载力计算结果对比Table 2 Comparisons between calculation and test results of flexural capacity
分析图表可以看出:在相同结构及截面设计情况下,随着界面连接程度的降低,结构承载力明显下降,笔者模型的计算结果与试验结果吻合良好,且荷载位移曲线的特征与试验结果基本一致。同时,采用传统纤维梁单元模型分析了完全刚性连接下的结构响应,试验梁下缘屈服时结构变形为6.57 mm,极限抗弯承载力为104.7 kN·m。可以看出,不考虑界面滑移效应将造成对结构刚度和承载力的高估。
2.2 负弯矩加载试验梁分析验证
选取文献[7]中SCB-10作为分析案例验证笔者所建模型对于负弯矩加载下力学行为分析的适用性。图6为SCB-10试验梁的示意图,栓钉间距为190 mm,单位长度的抗剪连接切线刚度ρs为270 MPa,截面设计参数如前文所述。所采用的计算单元模型、材料本构关系和边界条件与2.1节一致。

图6 负弯矩加载试验梁示意图Fig.6 Schematic diagram of test beams under negative moment loading
根据试验梁抗剪连接键设计,采用笔者所建模型计算加载全过程的力学行为;同时,采用传统纤维梁单元模型分析了完全刚性连接下的结构性能进行对比。荷载位移曲线的试验结果与模拟结果的对比情况如图7所示。模拟结果与试验结果基本吻合,界面滑移作用对该试验梁承载力影响不大。

图7 负弯矩加载试验梁荷载位移曲线Fig.7 Load-displacement curves of test beams under negative moment loading
3 结 论
(1)笔者建立的单元理论模型经验证可适用于钢-混凝土组合梁在弹性及弹塑性加载下的界面滑移效应及结构非线性行为计算分析;与试验结果相比,笔者建立的单元模型对结构变形的估计偏差在8.6%以内,抗弯承载力的估计偏差在1.7%以内。
(2)根据案例参数分析结果,钢混组合梁弱抗剪连接(栓钉间距2 000 mm)相较完全抗剪连接(栓钉间距取趋向于0的小值),正、负弯矩加载下结构变形均增大约50%,负弯矩抗弯承载力下降约19%,正弯矩抗弯承载力下降约47%,滑移效应对正弯矩承载力影响程度显著高于负弯矩承载力。
(3)笔者建立的理论模型为考虑滑移效应的钢-混组合梁非线性力学性能的分析与评估提供了一种较为简洁高效的分析方法。

