徐变效应下曲线组合梁界面滑移与轴向力解析法计算

王连广，崔景峰，裴家兴

(东北大学资源与土木工程学院，辽宁 沈阳 110819)

钢-混凝土组合梁(简称组合梁)是钢梁与混凝土板通过抗剪连接件协同作用的组合结构形式，能够充分发挥各构件性能的优势[1]。目前栓钉-柔性抗剪连接件在组合梁中的应用较为广泛，但在竖向荷载作用下，不可避免地会出现界面滑移，降低组合梁刚度和承载力[2]。同时，由于混凝土徐变效应，组合梁会产生内力和应力重分布，进一步增加界面滑移。对组合梁界面滑移与轴向力的研究，在考虑短期荷载效应的同时，还需考虑混凝土板的徐变效应，否则将给组合梁长期使用带来无法估测的损害。此外，与直线组合梁相比，曲线组合梁因其几何构型还需考虑弯扭同时作用，结构性能分析更为复杂。

国内外学者对于徐变效应下组合梁的研究主要从理论计算、数值模拟和试验分析三个方向进行[3-10]。朱力等[11]对组合梁变形、滑移等性能开展了一系列试验探究，提出了更高精度钢-混凝土组合箱梁考虑滑移效应的理论模型；X.Liu等[12-13]对平面弯曲组合梁挠度、滑移及扭转等开展了研究，利用大型有限元软件ABAQUS及室内试验验证了所提数值方法的精确性和效率，并证实了徐变作用会显著影响曲线组合梁的长期性能；A.Souici等[14]在考虑徐变效应的基础上给出了组合梁广义内力的时间表达式，能够预测组合梁在任意时刻的应力和应变状态，但未考虑界面滑移的影响；项贻强等[2]构建了体外预应力钢-混组合梁长期滑移微分方程并给出通解，其研究结论仅限于直线组合梁。

目前，国内外研究主要集中在直线组合梁短期性能上，忽略了混凝土徐变效应，对曲线组合梁长期性能的研究更是有限。因此，笔者基于弹性理论和龄期调整有效模量法(AEMM)，构建了徐变效应下曲线组合梁界面滑移与轴向力微分方程并给出其通解，结合算例分析了徐变效应对曲线组合梁长期性能的影响。研究结果表明，曲线组合梁界面滑移与轴向力变化曲线受作用荷载及滑移刚度影响较大，在设计中应着重考虑。

1 计算模型

1.1 研究对象

考察如图1所示的曲线组合梁，上部为混凝土板，下部为工字型钢梁，对应高度为hc和hs，总高度h=hc+hs，两者之间采用柔性连接件-栓钉连接。将曲线组合梁轴切线方向设为z轴，沿半径方向设为x轴，垂直于xoz平面向下设为y轴，y轴与x轴、z轴形成正交坐标系且遵循右手螺旋定则，R为平面曲率半径。

图1 曲线组合梁坐标系及界面应变分布Fig.1 Coordinate system and strain distribution of the curved composite beam

根据建立的曲线组合梁模型，取微段dz，对应角度dθ，力矩平衡和界面滑移如图2所示。Ac、Ic和As、Is分别为混凝土板和钢梁的截面面积、形心处截面惯性矩。

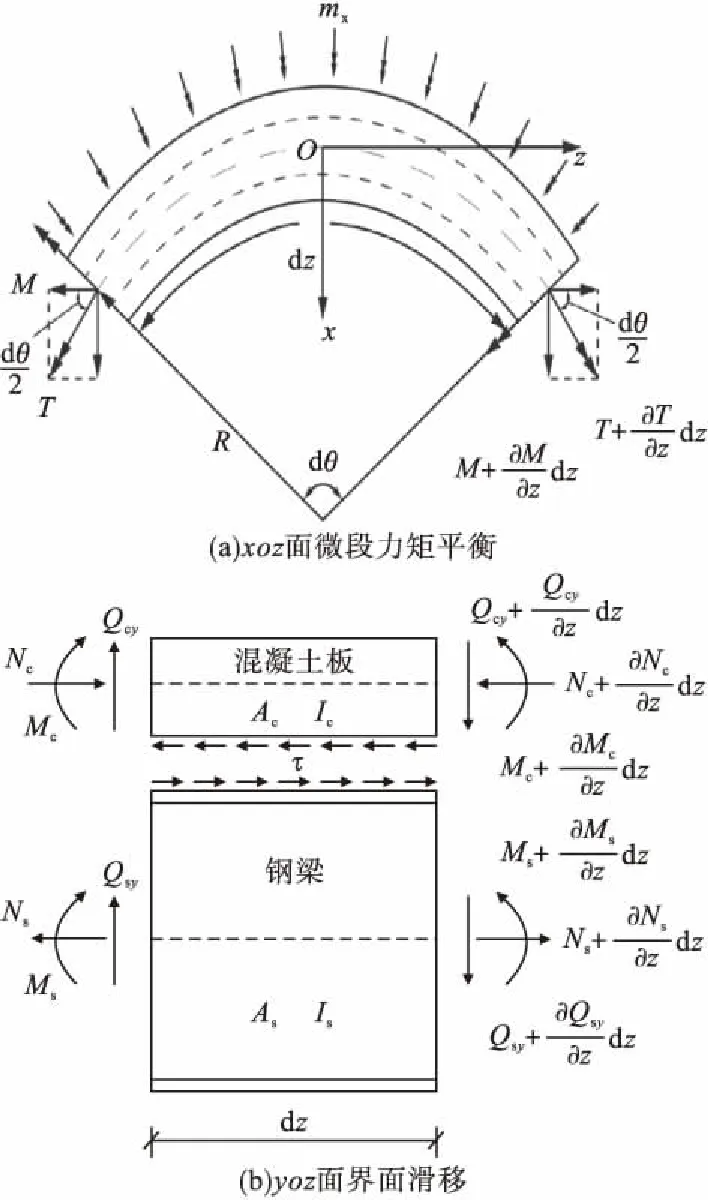
图2 微段力矩平衡和界面滑移Fig.2 Torque equilibrium diagram of micro-segment and slip diagram

F.Gara等[15]研究分析表明，荷载作用下，钢梁进行弹性工作，混凝土板最大压应变位于应力-应变曲线的上升段。为简化分析模型，将曲线组合梁近似按弹性体考虑，依据文献[16-17]，作如下基本假定：

(1)交界面处无竖向掀起，即钢梁与混凝土板曲率保持一致；

(2)混凝土板与钢梁各自符合平截面假定；

(3)抗剪连接件沿梁长等距分布，t时刻单位梁长切线方向剪切应力τ(t)与界面滑移S(t)呈线性关系，即：

τ(t)=kS(t).

(1)

式中：k为单位梁长滑移刚度，k=K/m，其中，K为连接件剪切刚度，m为连接件z向间距。

外荷载作用下曲线组合梁各构件除产生绕各自形心轴的弯矩Mc(t)和Ms(t)以及轴力Nc(t)和Ns(t)外，同时还会产生集中扭矩T。由图2及基本假定可得：

(2)

(3)

(4)

(5)

式中：φ为曲线组合梁扭转角；G、Id分别为曲线组合梁剪切模量和绕z轴的抗扭惯性矩；M(t)、Qy和mx分别为曲线组合梁总弯矩、竖向剪力和绕x轴的分布扭矩。

1.2 曲线组合梁各构件应变

取任意时刻t与任意z处典型截面，钢梁顶部应变εs(t)和混凝土板底部应变εc(t,t0)分别表示为

εs(t)=σs(t)/Es.

(6)

εc(t,t0)=εe(t0)+εcr(t,t0).

(7)

式中：εe(t0)为弹性应变；εcr(t,t0)为徐变应变；其中，εe(t0)=σc(t0)/Ec；σs(t)为t时刻钢梁应力；σc(t0)为初始时刻混凝土板应力；Es、Ec分别为钢梁和混凝土的弹性模量。

1.3 徐变应变计算

徐变应变的确定是求解界面滑移问题的关键。笔者采用龄期调整有效模量法(AEMM)近似考虑徐变效应，建立混凝土徐变本构方程，该方程所表示的徐变本构关系目前在国际上应用最为广泛[18-21]：

(8)

2 界面滑移和轴向力解析解

2.1 微分方程

根据基本假定(1)，弯曲变形过程中钢梁顶部与混凝土板底部界面交接处无竖向掀起，二者具有绕x轴相同曲率κ(t)，曲率κ(t)表示为

(9)

式中：Ix为曲线组合梁绕x轴抗弯惯性矩；EIx=EcIcx+EsIsx，其中Icx、Isx分别为混凝土板和钢梁绕x轴的抗弯惯性矩。

式(6)、式(7)可化为

(10)

(11)

则滑移应变εslip(t)可表示为

εcr(t,t0).

(12)

(13)

对式(9)求一阶导数，代入式(4)、式(5)可得：

(14)

联立式(1)～式(3)和式(10)～式(14)，化简得徐变效应下曲线组合梁界面滑移微分方程为

(15)

其中，

根据基本假定(3)，单个连接件剪力与滑移呈线性关系，对式(1)求一阶导得：

(16)

将式(12)代入式(16)得：

(17)

基于姚玲森[22]推得考虑徐变作用后曲线组合梁中混凝土板受力平衡关系如下所示：

(18)

(19)

式中：Qcx、τcz(t)、τ(t)分别为任意时刻混凝土板径向剪力、轴向均布力和纵向剪应力。

对式(18)求一阶导得：

(20)

令N(t)=Nc(t)=-Ns(t)，联立式(10)、式(11)以及式(17)～ 式(20)，略去∂τcz(t)/∂z，化简得徐变效应下曲线组合梁截面轴向力微分方程为

(21)

其中，λ2=α2-1/R2；μ=-Kζ/m；η=-Kγ/m；ξ=-Kh/2Rm。

2.2 微分方程解析解

式(15)、式(21)表示的控制微分方程，不同荷载工况下具有不同解。笔者以作用均布荷载q的简支工字型曲线组合梁为例，利用边界条件，导出界面滑移与轴向力解析公式，荷载工况如图3所示。

图3 均布荷载作用Fig.3 Uniform load on simply supported curved beam

利用边界条件：

(22)

求得弯矩M(t)、集中扭矩T、扭转角φ和剪力Qy表达式如下：

(23)

(24)

(25)

(26)

将以上参数分别代入式(15)、式(21)，可得如下方程。

(1)界面滑移控制微分方程

S″(t)-α2S(t)=

(27)

式中：β′=βR2q；δ=-(βR+γ)q。

(2)轴向力控制微分方程

(28)

式中：η′=R2q[η-ξR/(GId)]；ξ′=ξRq/(GId)。

由于求解过程相对复杂，文中仅给出界面滑移和轴向力微分方程最终通解。

(1)界面滑移S(t)

(29)

(2)轴向力N(t)

(30)

3 设计参数分析

依据上述理论模型，取图4简支工字型曲线组合梁为例进行研究，为验证文中方法的有效性，曲线组合梁截面相关参数取自文献[10]。曲线组合梁平面弯曲转角θ为15°，跨度L=5.9 m，钢材与混凝土弹性模量Es、Ec分别为2.0×105MPa和2.51×104MPa，剪切模量Gs、Gc对应取7.7×104MPa、1.0×104MPa，剪切刚度K取84 kN/mm，间距m=600 mm，环境相对湿度为50%，作用荷载如图5所示。

图4 曲线组合梁几何尺寸Fig.4 Geometrical dimensions of curved composite beam

图5 自重和附加荷载Fig.5 Self-weight and superimposed load

徐变效应对曲线组合梁结构的长期性能有着重要影响，在进行组合梁界面滑移与轴向力分析之前，对笔者采取的徐变模型进行验证，计算结果如图6所示。可以看出文中计算方法与文献[10]和文献[11]的数据拟合较好，可作为分析依据。

图6 徐变系数Fig.6 Creep coefficients

3.1 界面滑移与轴向力

曲线组合梁在不同时刻(t=10 d，t=1 000 d)和不同平面弯曲转角(θ=5°，θ=15°，θ=30°)的纵向界面滑移曲线分别见图7和图8。

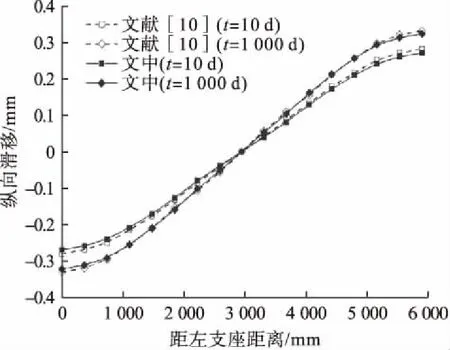
图7 不同时刻沿跨度纵向界面滑移Fig.7 Longitudinal interface slip at different ages along the span

图8 不同平面弯曲转角沿跨度纵向界面滑移Fig.8 Longitudinal interface slip of different plane bending angles along the span

由图可知，文中模型与文献[10]中结论吻合较好，验证了文中公式的合理性。图7和图8均表明滑移刚度k取140 MPa时，沿梁长方向的界面滑移量从梁两端部向跨中位置逐渐减小，两端最大，跨中滑移量为零且关于跨中呈反对称分布；相同跨距下靠近跨中位置处滑移变化量最大，向两端发展变化量越小。从图7可以看出，组合梁在荷载长期作用下，时间增大，滑移量随之增大；由图8可得，滑移量对不同平面弯曲转角变化的敏感度不大。

考虑徐变效应不同时刻沿梁长的纵向界面滑移见图9。由图可知，滑移量随龄期增长而增大，且前期增长率较快，而后逐渐减小。此外，滑移量在前178 d达到总滑移量的约80%，528 d左右基本趋于稳定。

图9 不同龄期沿跨度纵向界面滑移Fig.9 Longitudinal interface slip at different ages along the span

根据文中给出的轴向力理论模型，取初始时间28 d，最终时间1 028 d。不同时刻轴向力沿梁长的变化曲线见图10。

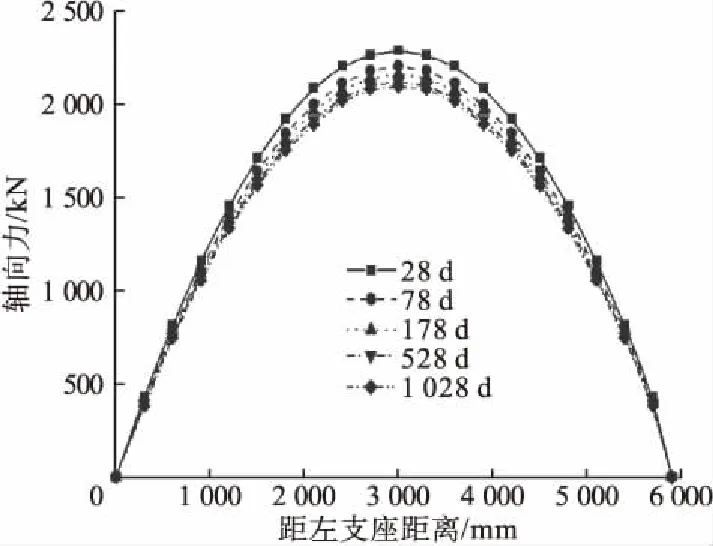
图10 不同龄期沿跨度轴向力Fig.10 Axial force at different ages along the span

图10中显示轴向力在梁端部值为零，跨中位置取得最大值且关于跨中呈对称分布，与滑移量最值发生位置恰好相反。同时表明，曲线组合梁的轴向力变化曲线前期变化率较大，528 d时轴向力值基本趋于稳定。

3.2 荷载和刚度变化影响

不同荷载作用下滑移增量与轴向力增量随龄期变化曲线分别见图11和图12。

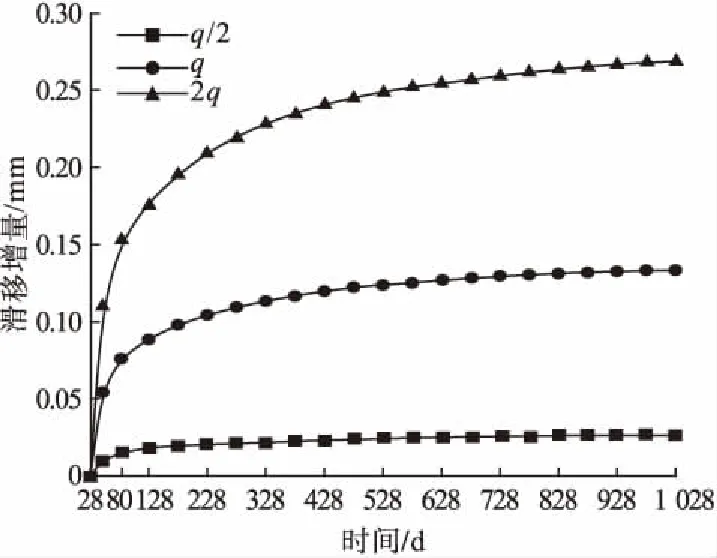
图11 不同荷载滑移增量-龄期变化曲线Fig.11 Slip increment-age curves under different loads

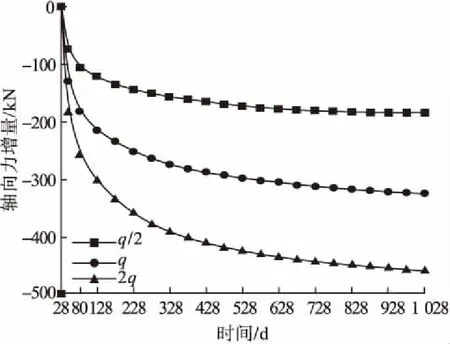
图12 不同荷载轴向力增量-龄期变化曲线Fig.12 Axial force increment-age curves under different loads

图11表示在28 d时，滑移增量为零，滑移量随龄期增加逐渐增大，且增长趋势为非线性。其中，大约在80 d前，滑移增量增加速率较大，与加载龄期几乎成正比；大约80 d之后滑移增量增长速率较为平缓，并且随着龄期的发展，后期滑移增量基本维持稳定。此外，伴随荷载的增加，界面滑移增量增大，且荷载越大，滑移增量变化曲线斜率越大。图12中轴向力增量变化趋势相似于滑移增量变化，区别在于轴向力增量随着龄期的增加而反向增大。

为进一步考察均布荷载q长期作用对界面滑移与轴向力的影响，图13和图14分别给出了不同连接刚度下滑移增量与轴向力增量随龄期变化曲线。

图13 不同连接刚度滑移增量-龄期变化曲线Fig.13 Slip increment-age curves under different connection stiffness

图14 不同连接刚度轴向力增量-龄期变化曲线Fig.14 Axial force increment-age curves under different connection stiffness

图13和图14表明，不同连接刚度下界面滑移与轴向力增量随时间延长而逐渐增大，变化趋势呈非线性。80 d之前界面滑移增量与轴向力增量增长速率较大，完成量占加载总龄期的约50%；128 d左右，完成量约占总量的80%，之后增加速率较为缓慢。另外，随着滑移刚度的增大，界面滑移增量减小，且连接件刚度越大，二者曲线斜率越小。从图14还可以看出，80 d前滑移刚度的变化对于轴向力增量变化几乎没有影响。

4 结 论

(1)对比文献[10]数值方法，文中给出的徐变效应下曲线组合梁界面滑移与轴向力解析法有效可行、且精度高。

(2)不同龄期曲线组合梁界面滑移与轴向力变化曲线呈反对称与对称分布，前178 d滑移量约为总量80%，随着龄期的增长，滑移量与轴向力变化逐渐减缓。此外，曲线组合梁滑移最大值出现在梁端，跨中不发生纵向滑移，而轴向力于跨中出现最大值，梁端无轴向力；滑移量对不同平面弯曲转角变化的敏感度不大。

(3)界面滑移与轴向力增量随龄期发展呈非线性趋势增大，且二者增量均随刚度增大而减小，滑移刚度越大，曲线斜率变化越小，与荷载作用趋势恰好相反。另外，80 d前，滑移刚度变化对轴向力增量的影响可以忽略不计；128 d左右时，界面滑移与轴向力增量约为总变化量的80%。