面向车辆路径问题的改进蚁群算法研究
刘紫玉 赵丽霞 薛建越 陈军霞 宋伟





摘 要:為解决基础蚁群算法在求解车辆路径问题时出现收敛速度慢、易陷入局部最优解等问题,提出了一种改进蚁群算法。首先,引入节约矩阵更新选择概率公式引导蚂蚁搜索;其次,运用分段函数改进挥发因子,调整算法的收敛速度;再次,使用2-opt法,提高算法的局部搜索能力;最后,选取车辆路径问题国际通用数据集进行仿真,运用控制变量法找到信息素因子和启发函数因子的合适取值,以P类数据测试算法的改进效果,并与基础蚁群算法、遗传算法、模拟退火算法和粒子群算法进行对比。结果表明,相较于基础蚁群算法,改进蚁群算法的最优路径总长度平均减少了6.97%;与遗传算法、模拟退火算法和粒子群算法相比,改进蚁群算法的寻优能力更强、收敛速度更快。因此,改进蚁群算法可以有效减少路径长度,跳出局部最优,加快收敛速度,尤其是在单路线允许服务点较多且各点分布较离散的车辆路径情况下,其优势更为明显,可为解决车辆路径问题提供一定的参考。
关键词:交通运输工程其他学科;基础蚁群算法;路径规划;挥发因子;2-opt法
中图分类号:F570 文献标识码:A
DOI:10.7535/hbkd.2022yx01009
收稿日期:2021-05-17;修回日期:2021-12-10;责任编辑:张士莹
基金项目:河北省社会科学基金(HB20GL011)
第一作者简介:刘紫玉(1975—),女,河北赵县人,教授,博士,主要从事物流与供应链、数据挖掘方面的研究。
E-mail:purpleyuliu@163.com
Research on vehicle routing problem based on improved ant colony algorithm
LIU Ziyu,ZHAO Lixia,XUE Jianyue,CHEN Junxia,SONG Wei
(School of Economics and Management,Hebei University of Science and Technology ,Shijiazhuang,Hebei 050018,China)
Abstract:In order to solve the problems of slow convergence and easiness to fall into local optimal solution in solving vehicle routing problem,an improved ant colony algorithm was proposed.Firstly,the saving matrix updating selection probability formula was introduced to guide ant search;Secondly,the piecewise function was used to improve the volatilization factor and adjust the convergence speed of the algorithm;Thirdly,the 2-opt method was used to improve the local search ability of the algorithm;Finally,the international general data set of vehicle routing problem was selected for simulation,and the control variable method was used to find the appropriate values of pheromone factor and heuristic function factor.The improvement effect of the algorithm was tested with class P data,and compared with basic ant colony algorithm,genetic algorithm,simulated annealing algorithm and particle swarm optimization algorithm.The results show that compared with the basic ant colony algorithm,the total length of the optimal path of the improved ant colony algorithm is reduced by 6.97%;Compared with genetic algorithm,simulated annealing algorithm and particle swarm optimization algorithm,the improved ant colony algorithm has stronger optimization ability and faster convergence speed.Therefore,the improved ant colony algorithm can effectively reduce the path length,jump out of the local optimization and accelerate the convergence speed.Especially in the case of a single route that allows more service points and discrete distribution of points,its advantages are more obvious,which provides a certain reference for solving the vehicle routing problem.
Keywords:
other disciplines of transportation engineering;basic ant colony algorithm;route planning;volatile factor;2-opt method
车辆路径问题(vehicle routing problem,VRP)指的是配送中心按照不同配送点的要求,安排车辆有序配送,找到满足约束的最优车辆调度方案。该问题属于NP难题。在求解VRP时,研究人员经常会使用精确式算法和元启发式算法。在求解小规模问题(节点数小于30)时,精确式算法独具优势,但当规模数量变大时,采用该算法会导致计算量过大,难以有效解决问题,适用面较窄。相比于精确式算法,元启发式算法更适合解决大规模问题,搜索更全面,可提高解的优良性,适用面也更广。蚁群算法具有鲁棒性、正反馈、并行性的优点,广泛用于解决车辆路径问题[1],但也会出现陷入局部最优解、收敛速度慢、效果不理想的情况。近年来,人们致力于改进蚁群算法的研究,提高其有效性和适用性,目前主要集中在流程改进和参数设置2个方面。
在流程改进方面,MOHAMED等[2]为解决带装载能力约束的车辆路径问题,提出一种结合局部搜索和蚁群算法的解决方法;KALAYCI等[3]为解决同时取送货车辆的路径问题,提出一种基于蚁群算法和可变邻域搜索的混合算法;ASGHARI等[4]为了找到社交网络中目标用户与客户端之间的可靠路径,设计了反向蚁群算法,更新后的信息素对蚂蚁选择的路径具有反向作用;潘颖等[5]将改进蚁群算法应用于解决系统软硬件划分问题,引入逆反馈机制提高蚁群算法的搜索性能;JOVANOVIC等[6]提出一种求解区域重定位问题的蚁群优化算法,将基本贪婪算法扩展到蚁群算法,给出定义信息素矩阵,提高了算法性能;BOUAMAMA等[7]将变邻域搜索作为子例程改进蚁群算法,求解最小连通支配集问题,该方法还可应用于加权和非加权问题变量;田鸽等[8]提出一种改进蚁群算法,对信息素更新方式加以扩大至最优解寻觅范围,并将启发因子的函数定义范围扩展至初始节点,利用2-opt(2-optimization)法进行局部优化;DECERLE等[9]提出一种将模因理论与蚁群算法相结合的混合算法,解决工作时间均衡的家庭医疗保健问题;MARTIN等[10]为解决家庭护理调度问题,提出一种动态邻域函数改进蚁群算法,提高了搜索能力;張恒等[11]提出一种改进双层蚁群算法,将蚁群划分为引导层蚁群和普通层蚁群;李广明等[12]为实现系统自适应动态推荐,改进了蚁群算法,针对不同搜索状态变更路径搜索策略,根据状态变化动态调整信息启发函数和期望函数,逐步完善了推荐策略;尹雅楠等[13]在规划无人机路径时改进了蚁群算法,对挥发因子以及信息素进行了上下设限。
在参数设置方面,原艳芳等[14]研究了采茶机器人路径问题,改进了蚁群算法,通过改变自适应调节信息素浓度值和迭代终止条件,提高全局搜索能力和计算效率;李根等[15]为解决室外移动机器人路径规划问题,优化了蚁群算法,运用单因素法对蚁群算法中的蚂蚁数目、信息素启发因子、期望启发因子、信息素挥发因子等参数进行分析研究,寻找到最优参数组合;万杰等[16]在研究VRP时设计了一种改进的蚁群算法,在启发因子中加入需求量和时间窗跨度因素;刘冠一等[17]在设计室内服务机器人路径导航系统时提出了自适应信息素浓度和动态信息素挥发因子,改进后的蚁群算法具有较高的全局搜索能力;刘辉等[18]提出采用改进蚁群算法实现高速列车的行车调度优化。
综合以上可以看出,在求解VRP改进蚁群算法时,人们只单方面关注流程的改进或是参数设置。由于基础蚁群算法在一开始搜索时具有盲目性,因而在实际操作中容易出现陷入局部最优解、收敛速度慢的情况。针对该情况,本文引入节约矩阵提高算法的全局搜索能力,运用分段函数改进挥发因子调整收敛速度,运用2-opt法提高算法的局部搜索能力。通过对蚁群算法流程和参数的综合改进,更好地求解车辆路径问题。
1 VRP数学模型的构建
VRP可以描述为配送中心按照不同配送点的要求,从配送中心出发,对所有配送点进行配送。每条配送路径的总载货量不可以超过车的最大承载能力,以确保每个配送点都能得到服务,一个配送点只能由一辆配送车提供服务。服务完配送路径最后一个配送点后,配送车要返回配送中心。为了找到满足约束的最小配送成本配送方案,做以下假设:(1)无缺货假设;(2)配送货物包装规则,无异型包装,配送货物按质量计算;(3)配送点需求量不会超过配送车的最大载重量。符号定义如表1所示。
模型构建如下:
min Z=∑mi=0∑mj=0∑nk=1dijxijk ,(1)
∑mi=0∑mj=0∑nk=1qixijk≤qmax ,(2)
∑mj=0xijk=∑mj=0xjik≤1 ,(3)
∑mi=0∑kk=1xijk=1,i∈M,i≠j,k∈K,(4)
∑mj=0∑kk=1xjik=1。(5)
式(1)表示目标函数,目标为总配送距离最短;式(2)表示配送车辆不可以超载;式(3)表示配送车辆出发后需要返回出发点;式(4)和式(5)表示每个配送点只能由一辆配送车配送。
2 改进蚁群算法的构建
2.1 基础蚁群算法
蚁群算法(ant colony optimization,ACO)是由意大利学者DORIGO等于20世纪90年代首先提出来的[19]。DORIGO等通过观察蚂蚁觅食发现,无论在任何情况下,蚁群最终都可以找到一条距离食物和洞穴最短的路径。看似简单的自然现象背后一定蕴含着科学原因。经过认真研究发现,“信息素”起着至关重要的作用。信息素是蚂蚁在爬行时分泌的一种特殊物质,正是这种特殊物质让蚂蚁在觅食时可以相互传递信息,实现交流。每只蚂蚁都会在爬行过的路径上分泌出“信息素”,信息素会有一定程度的挥发,其他蚂蚁在爬行时会感知到信息素的存在,也能分辨出信息素的浓度。蚂蚁在爬行时都会偏爱最短路径,这样一来蚂蚁就会在最短路径上分泌出信息素,别的蚂蚁感知到高浓度信息素的存在,会以更高的概率选择该路径,同时也会分泌出信息素。那些不是最短距离的路径也可能会被蚂蚁爬行,同样也留下信息素。随着时间的推移,较短路径上的信息素会越来越多,非较短路径上的信息素会越来越少。其他蚂蚁在觅食时也会选择最短路径进行爬行。不断循环往复后,最短路径上会有高浓度的信息素,所有的蚂蚁都会选择最短路径,至此蚁群找到了最短路径。
蚁群算法步骤如下。
1)初始化参数。
2)迭代次数NC=NC+1。
3)m只蚂蚁从起点出发。
4)选择下一个配送点。根据选择概率公式(6)和轮盘赌法选择下一个要到达的点:
pkijt=ταijtηβij∑j∈Nkjταijtηβij, j∈allowed,0, otherwise。(6)
式中:τij(t)为t时刻i,j两点间的信息素浓度,信息素浓度越高,蚂蚁选择该路径的概率越大;η为启发函数,η=1/dij,为i和j两点距离的倒数,两点距离越短,蚂蚁选择该路径的概率越大;allowed表示未访问点的集合。
5)判断是否历遍所有点,没有历遍返回步骤4),反之转到步骤6)。
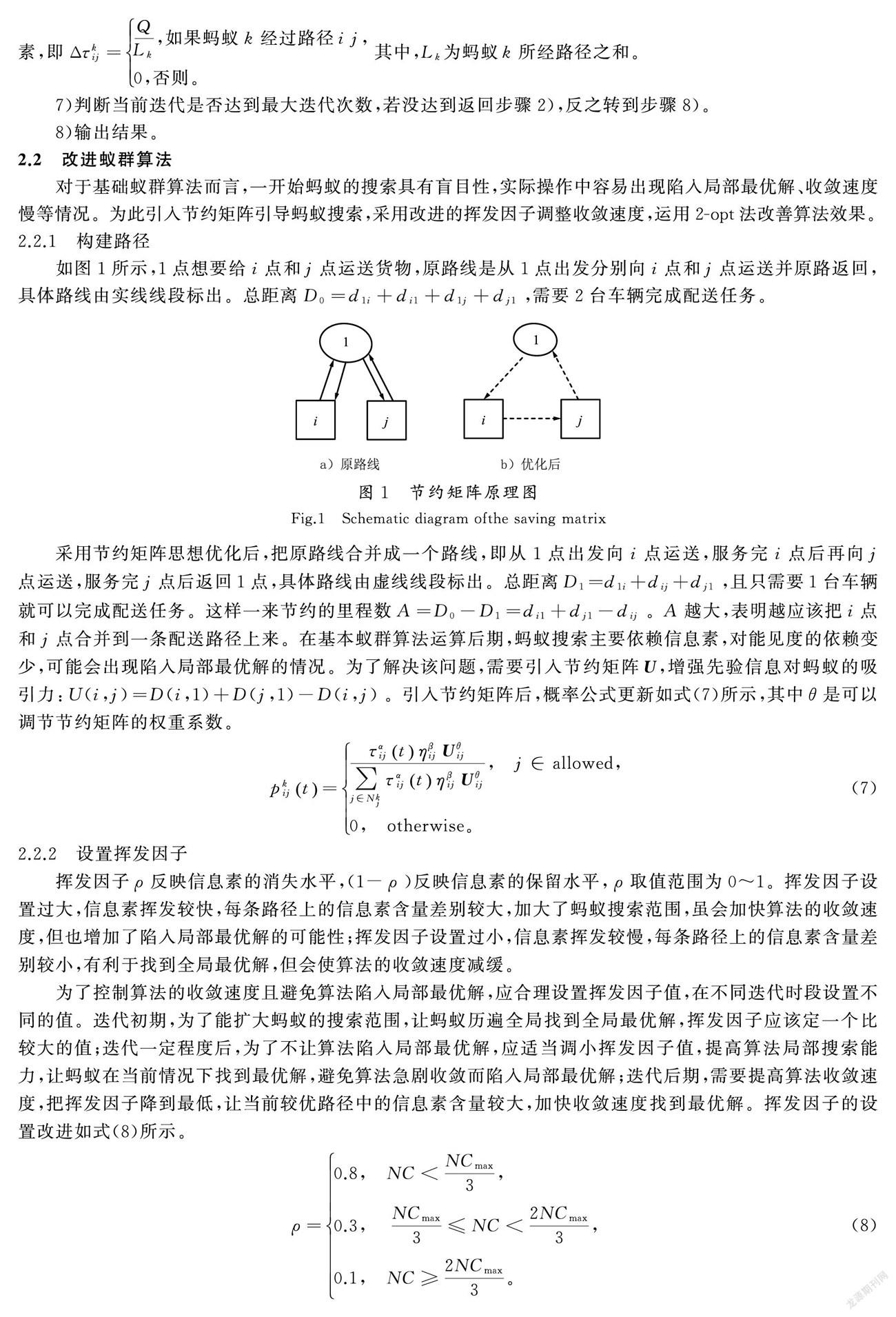
6)更新信息素。每只蚂蚁历遍所有配送点后需要更新信息素,按τij(t+1)=τij(t)*(1-ρ)+Δτij进行更新,其中Δτij为新增信息素含量,Δτij=∑mk=1Δτkij。这里采用的是蚁周模型,即历遍后蚂蚁才会释放信息素,即Δτkij=QLk,如果蚂蚁k经过路径i j,0,否则。其中,Lk为蚂蚁k所经路径之和。
7)判断当前迭代是否达到最大迭代次数,若没达到返回步骤2),反之转到步骤8)。
8)输出结果。
2.2 改进蚁群算法
对于基础蚁群算法而言,一开始蚂蚁的搜索具有盲目性,实际操作中容易出现陷入局部最优解、收敛速度慢等情况。为此引入节约矩阵引导蚂蚁搜索,采用改进的挥发因子调整收敛速度,运用2-opt法改善算法效果。
2.2.1 构建路径
如图1所示,1点想要给i点和j点运送货物,原路线是从1点出发分别向i点和j点运送并原路返回,具体路线由实线线段标出。总距离D0=d1i+di1+d1j+dj1,需要2台车辆完成配送任务。
采用节约矩阵思想优化后,把原路线合并成一个路线,即从1点出发向i点运送,服务完i点后再向j点运送,服务完j点后返回1点,具体路线由虚线线段标出。总距离D1=d1i+dij+dj1,且只需要1臺车辆就可以完成配送任务。这样一来节约的里程数A=D0-D1=di1+dj1-dij。A越大,表明越应该把i点和j点合并到一条配送路径上来。在基本蚁群算法运算后期,蚂蚁搜索主要依赖信息素,对能见度的依赖变少,可能会出现陷入局部最优解的情况。为了解决该问题,需要引入节约矩阵U,增强先验信息对蚂蚁的吸引力:U(i,j)=D(i,1)+D(j,1)-D(i,j)。引入节约矩阵后,概率公式更新如式(7)所示,其中θ是可以调节节约矩阵的权重系数。
pkijt=ταijtηβijUθij∑j∈NkjταijtηβijUθij, j∈allowed,0, otherwise。(7)
2.2.2 设置挥发因子
挥发因子ρ反映信息素的消失水平,(1-ρ)反映信息素的保留水平,ρ取值范围为0~1。挥发因子设置过大,信息素挥发较快,每条路径上的信息素含量差别较大,加大了蚂蚁搜索范围,虽会加快算法的收敛速度,但也增加了陷入局部最优解的可能性;挥发因子设置过小,信息素挥发较慢,每条路径上的信息素含量差别较小,有利于找到全局最优解,但会使算法的收敛速度减缓。
为了控制算法的收敛速度且避免算法陷入局部最优解,应合理设置挥发因子值,在不同迭代时段设置不同的值。迭代初期,为了能扩大蚂蚁的搜索范围,让蚂蚁历遍全局找到全局最优解,挥发因子应该定一个比较大的值;迭代一定程度后,为了不让算法陷入局部最优解,应适当调小挥发因子值,提高算法局部搜索能力,让蚂蚁在当前情况下找到最优解,避免算法急剧收敛而陷入局部最优解;迭代后期,需要提高算法收敛速度,把挥发因子降到最低,让当前较优路径中的信息素含量较大,加快收敛速度找到最优解。挥发因子的设置改进如式(8)所示。
ρ=0.8, NC<NCmax3,0.3, NCmax3≤NC<2NCmax3,0.1, NC≥2NCmax3。(8)
2.2.3 运用2-opt法
2-opt就是两元素优化,亦可称作2-exchange,核心在于随机选择路径上一个区间段进行优化,这个优化只是对当前一个状态的优化,并不是对全局的优化,所以是局部搜索算法。蚁群算法在迭代后期,有些路径上会因为距离短留下大量信息素,引导蚂蚁继续选择该路径,容易陷入局部最优解。
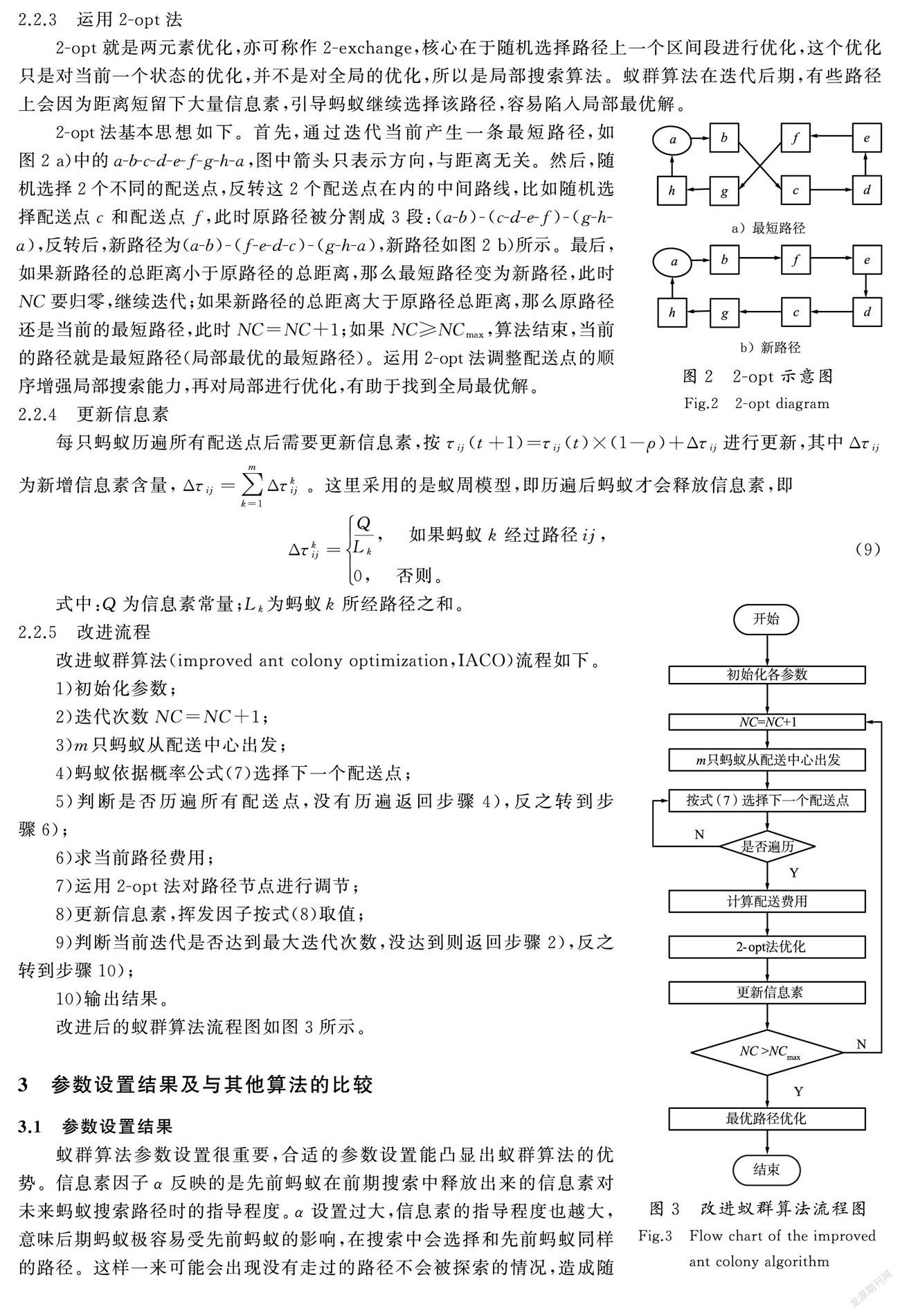
2-opt法基本思想如下。首先,通过迭代当前产生一条最短路径,如图2 a)中的a-b-c-d-e-f-g-h-a,图中箭头只表示方向,与距离无关。然后,随机选择2个不同的配送点,反转这2个配送点在内的中间路线,比如随机选择配送点c和配送点f,此时原路径被分割成3段:(a-b)-(c-d-e-f)-(g-h-a),反转后,新路径为(a-b)-(f-e-d-c)-(g-h-a),新路径如图2 b)所示。最后,如果新路径的总距离小于原路径的总距离,那么最短路径变为新路径,此时NC要归零,继续迭代;如果新路径的总距离大于原路径总距离,那么原路径还是当前的最短路径,此时NC=NC+1;如果NC≥NCmax,算法结束,当前的路径就是最短路径(局部最优的最短路径)。运用2-opt法调整配送点的顺序增强局部搜索能力,再对局部进行优化,有助于找到全局最优解。
2.2.4 更新信息素
每只蚂蚁历遍所有配送点后需要更新信息素,按τij(t+1)=τij(t)×(1-ρ)+Δτij进行更新,其中Δτij为新增信息素含量,Δτij=∑mk=1Δτkij。这里采用的是蚁周模型,即历遍后蚂蚁才会释放信息素,即
Δτkij=QLk, 如果蚂蚁k经过路径ij,0, 否则。(9)
式中:Q为信息素常量;Lk为蚂蚁k所经路径之和。
2.2.5 改进流程
改进蚁群算法(improved ant colony optimization,IACO)流程如下。
1)初始化参数;
2)迭代次数NC=NC+1;
3)m只螞蚁从配送中心出发;
4)蚂蚁依据概率公式(7)选择下一个配送点;
5)判断是否历遍所有配送点,没有历遍返回步骤4),反之转到步骤6);
6)求当前路径费用;
7)运用2-opt法对路径节点进行调节;
8)更新信息素,挥发因子按式(8)取值;
9)判断当前迭代是否达到最大迭代次数,没达到则返回步骤2),反之转到步骤10);
10)输出结果。
改进后的蚁群算法流程图如图3所示。
3 参数设置结果及与其他算法的比较
3.1 参数设置结果
蚁群算法参数设置很重要,合适的参数设置能凸显出蚁群算法的优势。信息素因子α反映的是先前蚂蚁在前期搜索中释放出来的信息素对未来蚂蚁搜索路径时的指导程度。α设置过大,信息素的指导程度也越大,意味后期蚂蚁极容易受先前蚂蚁的影响,在搜索中会选择和先前蚂蚁同样的路径。这样一来可能会出现没有走过的路径不会被探索的情况,造成随机搜索能力下降,解空间变小,容易陷入局部最优解。α设置过小,信息素的指导程度也越小,意味着先前蚂蚁的贡献重要程度变小,算法正反馈机制减弱,也容易陷入局部最优解。α的取值范围一般为[1,5][20]。
启发函数因子β反映的是启发函数在蚂蚁搜索路径时的指导程度。在基本蚁群算法中,将β设置为2点距离的倒数。β设置过大,蚂蚁在搜索时受到2点距离的影响越大,蚂蚁越容易选择局部最短路径,局部最短不意味着全局最短,从而会导致算法过早收敛,容易陷入局部最优解。相反,β设置过小,蚂蚁在搜索时不容易受启发函数的影响,出现完全随机搜索的情况,算法收敛会变慢,不容易找到最优解。β的取值范围一般为[1,5][20]。
本文采用针对VRP国际通用的数据集进行试验。该数据集有74个数据,名称有统一标准,即X-nY-kZ。X代表A,B,P不同类型,A类代表数据中各个配送点分布是半聚集半分散的,B代表聚集型,P代表分散型;Y代表点数(配送中心和配送点总和);Z为最大车辆使用数。例如:A-n32-k5,代表的是A类型32个点,允许最大使用车辆数为5的数据。数据集特点见表2。
本文只针对P类数据进行讨论。随机选择P-n22-k8对信息素因子α、启发函数因子β的取值进行试验,α和β在[1,5]区间内取整数两两组合,共有25种情况,对不同组合都进行10次运算,测试出合适的参数组合,运行结果如表3所示。
在表3可以看出,当α取值保持不变时,β取值越小,蚂蚁越不受2点距离的影响,陷入随机搜索,算法不易收敛;相反,随着β取值的不断变大,蚂蚁在搜索时几乎只考虑两点距离,很容易选择局部最短路径,导致算法过早收敛。当β取值保持不变时,α取值越大,蚂蚁在搜索时几乎只考虑先前蚂蚁留下的信息素,使得随机搜索能力下降,容易陷入局部最优解,运行出来的结果越来越差;相反,随着α取值的不断变小,前期蚂蚁做出的贡献重要程度也变小,不利于找到全局最优解。
由表3还可以看出,序号为17时算法效果较好。虽然平均迭代次数不是最小值,但迭代次数居中,最优路径距离总长度和最差路径距离总长度的和均为最短。因此,将α设置为4,β设置为2。调试参数组合的最优情况路径图如图4所示。
从图4 P-n22-k8最优路径图可以看出,物流中心服务的客户距离都较近,车辆路径鲜少出现交叉与迂回等现象,因此改进蚁群算法给车辆路径规划提供了更大的组合优化空间,能有效避免出现交叉配送与迂回运输不合理等现象,缩短车辆行驶距离,减少车辆使用数量,降低物流成本。
3.2 与基础蚁群算法的比较
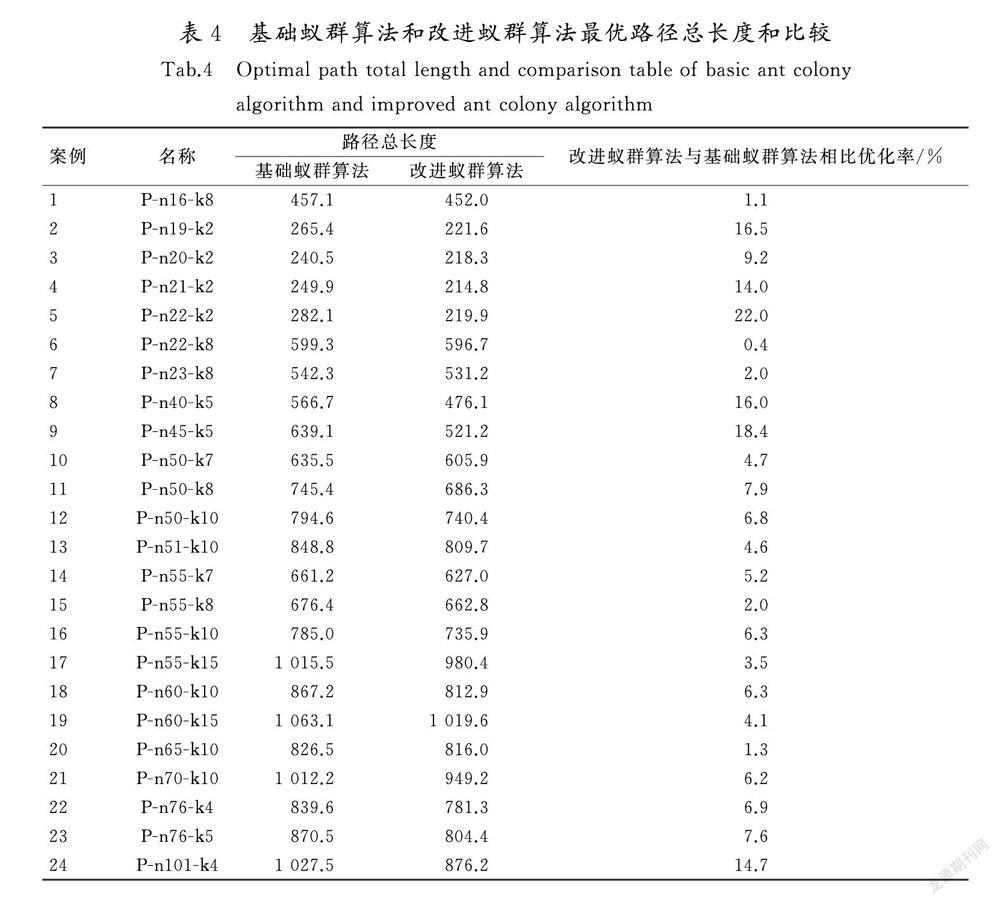
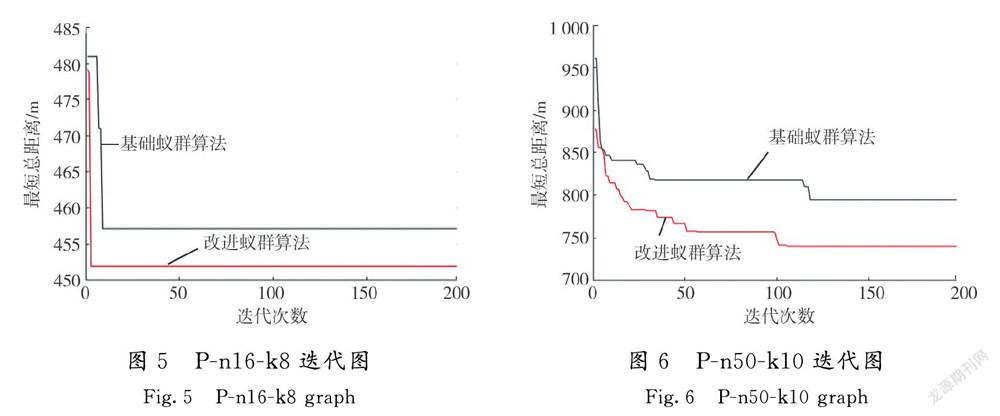
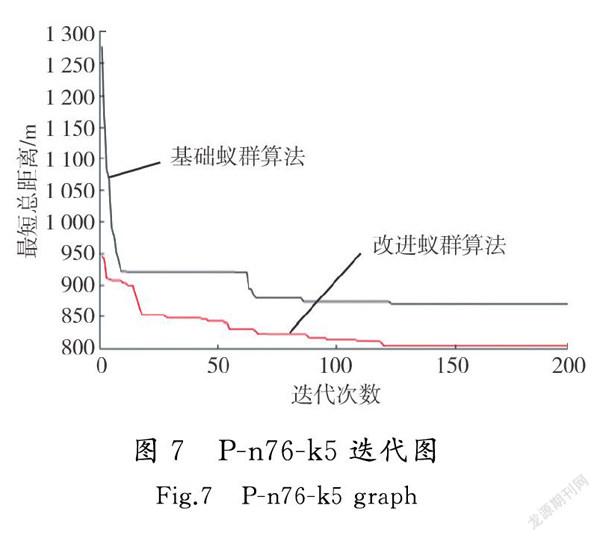
选择P类数据,运用基础蚁群算法和改进蚁群算法分别进行计算,基础蚁群算法中ρ=0.2[21],改进蚁群算法中θ=2。其他参数设置如下:m=节点数×1.5[22],Q=1 000,NCmax=200。使用MATLAB R2018a软件进行仿真,小规模问题、中规模问题和大规模问题的迭代曲线如图5—图7所示,不同案例最优路径总长度和比较如表4所示。
由图5—图7可以看出,在小规模问题下,基础蚁群算法和改进蚁群算法都在迭代初期找到最优解,但改进蚁群算法在搜索初期路径长度就小于基础蚁群算法,且收敛速度更快,更早跳出局部最优解;在中规模问题下,迭代初期改进算法的初始解优于基础蚁群算法,2种算法在迭代中期收敛,但改进蚁群算法更早跳出局部最优解,且收敛速度也要快于基础蚁群算法;在大规模问题下,2种算法在迭代初期相差较大,明显体现出改进算法的优势,且改进算法能够不断跳出局部最优,寻找更优解,2种算法虽都在迭代中后期收敛,但改进蚁群算法稍快于基础蚁群算法,寻优能力更强。
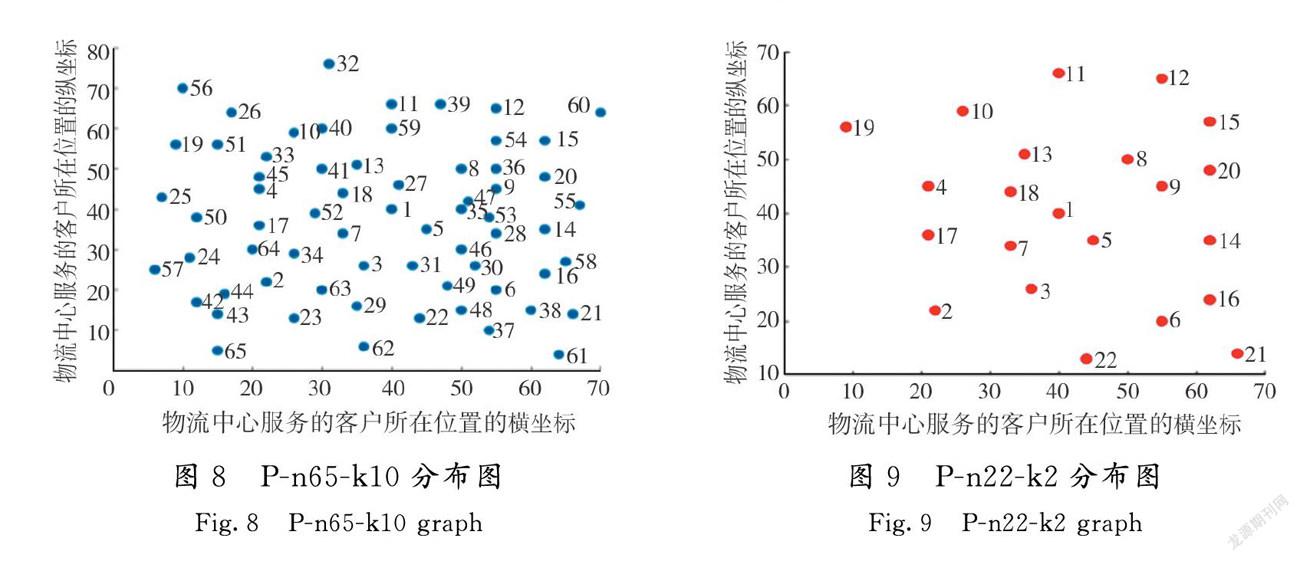
由表4可以看出,所有案例使用改进蚁群算法后都有不同程度的改善。与基础蚁群算法相比,改进蚁群算法平均距离减少了6.97%,大部分案例都减少6%以上,最多减少了22%。提升较少的案例原因有2点:一是因为单路线允许服务配送点较少(如案例1、案例6);二是各点分布较密集(如案例20,各点分布如图8所示),可优化的空间较小,所以改进蚁群算法的优势体现不出来。由此可以得出,本文提出的算法较适合于单路线允许服务点较多且各点分布较离散的VRP(如案例5,分布如图9所示)。
总体来看,改进蚁群算法明显优于基础蚁群算法。结合迭代图可以看出,改进后的蚁群算法仿真结果均优于基本蚁群算法,且在迭代初期改进蚁群算法的寻优能力就强于基础蚁群算法;此外,改进蚁群算法的收敛速度也快于基本蚁群算法。
3.3 与其他算法的比较
选择P类数据,运用基础蚁群算法和改进蚁群算法分别进行计算,基础蚁群算法中ρ=0.2[21],改进蚁群算法中θ=2。其他参数设置如下:m=节点数×1.5[22],Q=1 000,NCmax=200。使用MATLAB R2018a软件,运用遗传算法、模拟退火算法和粒子群算法分别进行仿真比较,结果如表5所示。
由表5可以看出,与遗传算法相比,改进蚁群算法共有17个案例最优路径总长度和减少。剩余案例中只有案例22、案例23遗传算法结果明显优于改进蚁群算法,其余相差不多。与模拟退火算法相比,共有15个案例最优路径总长度和减少,比较而言,改进蚁群算法对于小规模问题的改善程度较低。与粒子群算法相比,改进蚁群算法的仿真结果绝大部分都有改善,只有大规模问题提升效果不佳,共有18个案例的总路径长度减少。以案例6为例,不同算法的迭代图如图10所示。
由图10可以看出,在迭代初期几种方法相差较大,初始解明显体现出了改进算法的优势,且改进算法能够跳出局部最优寻找更优解;从解的质量来看,不论是初始解还是最优解,改进蚁群算法的寻优能力更强;从收敛速度来看,改进蚁群算法与粒子群算法都比较快,遗传算法较慢,模拟退火算法居中,但综合解的质量来说,还是改进蚁群算法的效果更好。因此,与其他算法相比,改进蚁群算法的寻优能力更强,收敛速度更快,最优路径距离总长度最短。
4 结 语
1)本文综合算法流程和参数设置对蚁群算法进行了改进:引入节约矩阵更新选择概率公式,提高了算法的全局搜索能力;运用分段函数改进挥发因子,合理加快了算法的收敛速度;引入2-opt法,提高了算法的局部搜索能力。
2)与基础蚁群算法、遗传算法、模拟退火算法和粒子群算法的仿真结果表明,不论小规模、中规模还是大规模问题,改进后的蚁群算法仿真结果均优于基本蚁群算法,尤其是在解决单路线允许服务点较多且各点分布较离散的VRP时,改进蚁群算法的优势更加凸显。
3)改进后的蚁群算法迭代初期解就优于基础蚁群算法,且改进蚁群算法的收敛速度快于基础蚁群算法,最优路径总长度的和也小于基础蚁群算法。
4)与遗传算法、模拟退火算法和粒子群算法相比,改进蚁群算法最优路径总长度的和绝大部分都有改善,迭代图也表明改进蚁群算法比其他3种算法的寻优能力更强,收敛速度更快。
改进蚁群算法不论在寻优能力方面还是在收敛速度方面都明显优于基本蚁群算法、遗传算法、模拟退火算法和粒子群算法,为解决VRP提供了新思路。本文提出的算法针对VRP虽有普遍适用性,但是细分VRP有很多类型,比如动态VRP、同时取送货VRP等。为了提高算法的适用性,本文并没有对每一种类型的VRP进行针对性的改进,未来可就此进行深入探讨,还可以进一步改进蚁群算法,使其应用于更多领域。
参考文献/References:
[1] 庞燕,罗华丽,邢立宁,等.车辆路径优化问题及求解方法研究综述[J].控制理论与应用,2019,36(10):1573-1584.
PANG Yan,LUO Huali,XING Lining,et al.A survey of vehicle routing optimization problems and solution methods[J].Control Theory & Applications,2019,36(10):1573-1584.
[2] MOHAMED M M S,GAJPALB Y,ELMEKKAWYC T Y,et al.Hybridized ant colony algorithm for the multi compartment vehicle routing problem[J].Applied Soft Computing,2015,37:196-203.
[3] KALAYCI C B,KAYA C.An ant colony system empowered variable neighborhood search algorithm for the vehicle routing problem with simultaneous pickup and delivery[J].Expert Systems with Applications,2016,66:163-175.
[4] ASGHARI S,AZADI K.A reliable path between target users and clients in social networks using an inverted ant colony optimization algorithm[J].Karbala International Journal of Modern Science,2017,3(3):143-152.
[5] 潘穎,阮文惠.基于改进蚁群算法的嵌入式系统软硬件划分[J].现代电子技术,2017,40(3):164-166.
PAN Ying,RUAN Wenhui.Embedded system hardware and software partition based on improved ant colony algorithm[J].Modern Electronics Technique,2017,40(3):164-166.
[6] JOVANOVIC R,TUBA M,VO S.An efficient ant colony optimization algorithm for the blocks relocation problem[J].European Journal of Operational Research,2019,274(1):78-90.
[7] BOUAMAMA S,BLUM C,FAGES J G.An algorithm based on ant colony optimization for the minimum connected dominating set problem[J].Applied Soft Computing,2019,80:672-686.
[8] 田鸽,薛冬娟,梁斌,等.基于改进蚁群算法的冰鲜水产品配送路径优化方法研究[J].大连海洋大学学报,2019,34(5):746-751.
TIAN Ge,XUE Dongjuan,LIANG Bin,et al.Distribution route and its optimization of chilled fishery products[J].Journal of Dalian Fisheries University,2019,34(5):746-751.
[9] DECERLE J,GRUNDER O,HASSANI A H E,et al.A hybrid memetic-ant colony optimization algorithm for the home health care problem with time window,synchronization and working time balancing[J].Swarm and Evolutionary Computation,2019,46:171-183.
[10]MARTIN E,CERVANTES A,SAEZ Y,et al.IACS-HCSP:Improved ant colony optimization for large-scale home care scheduling problems[J].Expert Systems with Applications,2020,142.DOI.10.1016/j.eswa.2019.112994.
[11]張恒,何丽,袁亮,等.基于改进双层蚁群算法的移动机器人路径规划[J/OL].控制与决策.[2021-01-05].https://kns.cnki.net/kcms/detail/detail.aspx?FileName=KZYC20210104002&DbName=CAPJ2021.
ZHANG Heng,HE Li,YUAN Liang,et al.Mobile robot path planning using improved double-layer ant colony algorithm[J/OL].Control and Decision.[2021-01-05].https://kns.cnki.net/kcms/detail/detail.aspx?FileName=KZYC20210104002&DbName=CAPJ2021.
[12]李广明,付剑锋.基于用户搜索状态的动态推荐模型研究[J].情报理论与实践,2021,44(7):166-172.
LI Guangming,FU Jianfeng.Research on dynamic recommendation model based on user search state[J].Information Studies Theory & Application,2021,44(7):166-172.
[13]尹雅楠,甄然,武晓晶,等.自适应多启发蚁群算法的无人机路径规划[J].河北科技大学学报,2021,42(1):38-47.
YIN Yanan,ZHEN Ran,WU Xiaojing,et al.Research on UAV route planning based on adaptive multi heuristic ant colony algorithm[J].Journal of Hebei University of Science and Technology,2021,42(1):38-47.
[14]原艳芳,郑相周,林卫国.名优茶采摘机器人路径规划[J].安徽农业大学学报,2017,44(3):530-535.
YUAN Yanfang,ZHENG Xiangzhou,LIN Weiguo.Path planning of picking robot for famous tea[J].Journal of Anhui Agricultural University,2017,44(3):530-535.
[15]李根,李航,张帅阳,等.基于蚁群算法的最优路径规划及参数研究[J].中国科技论文,2018,13(16):1909-1914.
LI Gen,LI Hang,ZHANG Shuaiyang,et al.Optimal path planning and parameter analysis based on ant colony algorithm[J].China Science Paper,2018,13(16):1909-1914.
[16]万杰,耿丽,田喆.基于改进的蚁群算法求解多目标生鲜农产品车辆路径[J].山东农业大学学报(自然科学版),2019,50(6):1080-1086.
WAN Jie,GENG Li,TIAN Zhe.Solution for the vehicle route of multi-objective fresh agricultural products based on the improved ant colony algorithm[J].Journal of Shandong Agricultural University(Natural Science Edition),2019,50(6):1080-1086.
[17]刘冠一,窦水海,杜艳平,等.室内服务机器人路径导航系统设计及算法[J].科学技术与工程,2020,20(34):14114-14119.
LIU Guanyi,DOU Shuihai,DU Yanping,et al.Algorithm and design of path navigation system of indoor service mobile robot[J].Science Technology and Engineering,2020,20(34):14114-14119.
[18]刘辉,代学武,崔东亮,等.基于参数自适应蚁群算法的高速列车行车调度优化[J].控制与决策,2021,36(7):1581-1591.
LIU Hui,DAI Xuewu,CUI Dongliang,et al.Optimization of high-speed train operation scheduling based on parameter adaptive improved ant colony algorithm[J].Control and Decision,2021,36(7):1581-1591.
[19]DORIGO M.Optimization,Learning and Natural Algorithms[D].Milan:Politecnicodi Milano,1992.
[20]史恩秀,陳敏敏,李俊,等.基于蚁群算法的移动机器人全局路径规划方法研究[J].农业机械学报,2014,45(6):53-57.
SHI Enxiu,CHEN Minmin,LI Jun,et al.Research on method of global path-planning for mobile robot based on ant-colony algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(6):53-57.
[21]杜玉红,张岩,赵焕峰.基于参数优化蚁群算法的机器人路径规划研究[J].现代制造工程,2020(9):7-14.
DU Yuhong,ZHANG Yan,ZHAO Huanfeng.Research on robot path planning based on parameters optimized ant colony optimization[J].Modern Manufacturing Engineering,2020(9):7-14.
[22]张松灿,普杰信,司彦娜,等.基于种群相似度的自适应改进蚁群算法及应用[J].计算机工程与应用,2021,57(8):70-77.
ZHANG Songcan,PU Jiexin,SI Yanna,et al.Adaptive improved ant colony algorithm based on population similarity and its application[J].Computer Engineering and Applications,2021,57(8):70-77.
3493500338284

