动态多流形投影算法在统计过程监测中的应用

郭金玉 王霞

摘 要：為了解决工业数据的序列相关性以及数据的全局和局部结构在某些异常状态下的变化问题，通过“时滞偏移”方法将动态行为纳入多流形投影（multi-manifold projections，MMP）模型，提出一种动态多流形投影算法（dynamic multi-manifold projections，DMMP）在统计过程监测中的应用方案。首先，在原始采样数据的基础上加入时滞变量使之具有动态特性;其次，通过分别求解全局图最大值和局部图最小值，获得全局和局部结构信息;然后，构建统一框架，即全局图最大值和局部图最小值，提取高维动态数据有意义的低维描述;最后，通过对比统计量与控制限进行故障检测，将基于DMMP的监控方案通过田纳西-伊斯曼过程验证其可行性和有效性。仿真结果表明，DMMP的整体性能优于一些传统的保持全局或局部特征的算法。新算法解决了传统算法中具有时间相关性的数据信息获取不全面的问题，为提高传统算法在动态工业过程故障检测中的性能提供了参考。

关键词：自动控制其他学科;统计过程监测;全局图;局部图;时滞偏移;动态多流形投影

中图分类号：TP277   文献标识码：A

DOI：10.7535/hbkd.2022yx01002

收稿日期：2021-11-22;修回日期：2021-12-23;责任编辑：王淑霞

基金项目：国家自然科学基金（61673279）;辽宁省教育厅科学研究项目（LJ2019007）

第一作者简介：郭金玉（1975—），女，山东高唐人，副教授，博士，主要从事故障诊断、生物特征识别算法及应用方面的研究。

通讯作者：郭金玉副教授。E-mail：969554959@qq.com

Application of dynamic multi-manifold projections algorithmin statistical process monitoring

GUO Jinyu，WANG Xia

（College of Information Engineering，Shenyang University of Chemical Technology，Shenyang，Liaoning 110142，China）

Abstract：To solve the problem of serial correlation of industrial data and the changes of global and local structure of data in some abnormal states，the "time lag migration" method was used to incorporate dynamic behavior into the multi-manifold projections（MMP） model，and an application scheme of dynamic multi-manifold projections（DMMP） algorithm in statistical process monitoring was proposed.Firstly，time-lag variables were added to the original sample data to make it dynamic.Secondly，the global and local structure information was obtained by solving the global graph maximum and local graph minimum separately.A unified framework，i.e.global graph maximum and local graph minimum，was constructed to extract meaningful low-dimensional representations for high-dimensional dynamic data.Finally，the fault detection was performed by comparing the statistics with control limits.The feasibility and effectiveness of the monitoring scheme based on DMMP was verified by the Tennessee-Eastman process.The simulation results show that the overall performance of DMMP is better than those of some traditional preserving global or local feature algorithms.The new algorithm solves the problem of incomplete acquisition of time-dependent data information in traditional algorithms，and provides a reference for improving the performance of traditional algorithms in fault detection of dynamic industrial process.

Keywords：

other disciplines of automatic control technology;statistical process monitoring;global graph;local graph;time lag migration;dynamic multi-manifold projections

随着中国向高质量方向发展的迈进，现代工业生产过程日趋精细化、复杂化，因此必须保证生产操作系统不出现任何故障。因为每个系统之间都是相互关联的，其中任何一个故障若不能及时被检测出来都可能对生产过程造成巨大威胁，影响产品质量，因此提高控制系统的稳定性、保证生产过程的安全性和可靠性变得至关重要。近年来，基于数据驱动的故障检测算法广受学术界关注，其利用集散控制系统采集的大量过程测量数据，通过压缩提取将有用的信息用于故障检测和诊断。以主成分分析（principal component analysis，PCA）、偏最小二乘法（partial least squares，PLS）和独立成分分析法（independent component analysis，ICA）为代表的多元统计学方法在过程监测领域得到了广泛应用[1-5]。

随着自动收集多元数据集技术的发展，对统计过程监测潜在变量的需求也随之增加。在统计过程监控中，JOLLIFFE等[6]和VANHATALO等[7]提出PCA依赖于数据在时间上独立的假设，然而生产过程收集的数据呈现出一系列的时间相关性，在当今应用中，这种假设变得越来越不现实。MONTGOMERY等[8]在研究中解释了这种现象，是因为系统动力学与高频采样相结合，从而连续观测就会连续相关。VANHATALO等[7]也证明了自相关对基于PCA的统计过程监控的负面影响。为了克服单模型、非动态的建模方式，VANHATALO等[9]针对工业过程数据呈现的动态特性，提出一种用于统计过程监控的动态主成分分析（dynamic principal component analysis，DPCA）算法。田宇[10]提出一种优化动态核主元分析的故障诊断算法，该算法突破了传统算法的局限，构建一个适合处理非线性和动态数据的模型。虽然上述算法都对故障检测具有良好的檢测效果，但是在进行数据处理时只保留了样本的全局信息，忽略了局部信息对数据的影响，这就造成了局部信息的缺失。因此在学术界寻找可以保留样本邻域结构的新算法成为关注的焦点。HE等[11]为了研究数据的局部结构特征，提出邻域保持嵌入算法，有效保持了原始数据的邻域信息。HU等[12]提出局部保持投影（locality preserving projections，LPP）算法。与其他流形学习算法相比，LPP算法具有一个显著的优点，即能够容易获得一个显式的线性映射。但是，LPP算法存在一个弊端，即LPP的降维性能可能会因为丢失采样数据全局结构中存在的一些重要信息而降低。因此，全局和局部结构对于过程监控至关重要。因为全局结构定义过程数据集的外部形状，而局部结构呈现数据集的内部组织。研究人员又将目光转移到全局与局部结合的新算法来提高故障检测性能。ZHANG等[13]提出一种用于故障检测的全局-局部结构分析（global-local structure analysis，GLSA）模型，其性能优于基于PCA和LPP的监测算法。TONG等[14]基于流形学习的邻域嵌入能力，提出一种新的多流形投影算法（multi-manifold projections，MMP）。MMP的目标是找到一个最优的投影来降维表示原始数据，这个低维数据可以同时最佳地保持全局和局部结构。

如今的工业过程数据趋于动态性，被监测的工业过程数据变量通常是连续自相关的，依赖于数据与时间无关假设的PCA在统计过程监控中受到了限制。KU等[15]提出动态主成分分析来弥补PCA的不足，DPCA算法能够提取过程的动态变化信息，其在化工过程故障检测方面的有效性已经得到验证[16]。有学者在LPP算法的基础上提出动态局部保持投影（dynamiclocality preserving projections，DLPP）算法以提高监控性能。由于过程数据的动态特性，静态情况下的多流形投影算法已经无法满足要求，导致故障检测效果不佳。因此，如何克服数据呈现的动态特性并且最佳地保持数据的全局和局部信息成为研究的重要内容。针对工业数据表现出的时间相关性，本文提出一种动态多流形投影（dynamic multi-manifold projections，DMMP）算法，并且将其用于TE过程进行故障检测。

1 动态多流形投影算法

在过程数据朝动态特性发展的趋势下，张成等[17]提出了基于 DPCA 残差互异度的故障检测与诊断算法，有效降低了动态特征对故障检测的影响，但是忽略了样本的局部信息。DLPP算法能保持数据的局部信息，但是会丢失方差信息，从而破坏样本的外部形状。针对2种算法的局限性，本文通过引入动态多流形投影算法，使得故障检测模型对数据的动态特性有更强的捕捉性能，改善模型的过程监测性能。

本质上DMMP的工作方式与MMP相同。首先使用时间滞后偏移方法将包含n个原始样本的数据集X=x1，x2，…，xi…，xnT（其中xi∈Rm）转换为新的包含过程静态和动态特征的增广矩阵X，然后在X上执行MMP算法。若过程的时滞参数lag=l，通常情况下线性系统的时滞参数l为1或2，若是非线性系统，则l的数值更大，以便得到实际非线性系统的良好线性逼近。通过式（1）生成增广矩阵X：

X=[x1，x2，…，xi，…xn]T，（1）

式中：xi=xTi，xT（i-1），…，xT（i-l）T。

对增广矩阵X进行标准化处理，然后利用图的邻域嵌入能力，为MMP算法构造统一的对偶优化函数，并分别定义局部图最小值和全局图最大值。

局部图最小值的目标函数与LPP[18]相同，先计算邻接矩阵W。局部保持函数为

Jp=min1n∑ni，j=1pTxi-xjWijxi-xjTp=

minpTXTD-WXp=

minpTXTLXp=

minpTL′p，（2）

其中

Wij=exp-‖xi-xj‖2/c，  xi，xj∈Nxi，xj，0，  其他，（3）

式中：L=D-W，在流形学习中称为拉普拉斯矩阵;L′=pTXTLX定义为局部图矩阵;D是一个对角线矩阵;对角线元素为邻接矩阵W的列（或行）之和。

对于全局图最大值目标函数，需要嵌入邻域信息来获得最佳外部形状的流形结构。与传统PCA模型中的平均中心不同，需要考虑每个样本xi的局部平均向量xi，可以比原始数据的平均中心向量更加独立。xi的局部均值向量为

xi=1ni∑xjxj∈Nxi，xj，  i=1，2，…，n，（4）

式中：ni是Nxi，xj中的样本数，所有样本的局部平均向量为Xi=x1，x2，…，xnT。在此基础上，通过最大化下列目标函数来计算投影p。

Jp=max∑ni=1pTxi-xixi-xiTp=

maxpTX-XiTX-Xip=

maxpTGp，（5）

式中：G=X-XiTX-Xi为全局图矩阵。

通过上述过程将数据的局部和整体结构同时保存在DMMP中。根据图的嵌入能力，DMMP应满足2个优化标准，即全局图最大值和局部图最小值，然后通过最大化以下函数来求解满足条件的投影p。

JDMMP=maxpTX-XiTX-XippTXT（D-W）Xp=maxpTGppTL′p，（6）

将式（6）简化为广义的特征值问题：

Gp=λL′p。（7）

假设p1，p2，…，pd是对应于方程（7）的d个最大特征值λ1，λ2，…，λd的特征向量，捕获全局和局部信息的低维矩阵Y如下：

Y=XP（PTP）-1。（8）

式中：P为负载矩阵，P=p1，p2，…，pd∈Rm×（l+1）×d;Y=y1，y2，…，ynT∈Rn×d。

故障检测中通常用平方预测误差（squared prediction error，SPE）和T2统计量指标来分析故障检测准确性，当检测值超过控制限，则系统会将超过控制限的检测点认为是故障。SPE和T2统计量的计算如下：

E=X-YPT，（9）

SPE=EET，（10）

T2=XPλ-1PTXT。（11）

MMP是在一个无监督的方式下将邻域信息嵌入到全局和局部信息中，因此在一定程度上保留了判别特征和聚类信息。在数据分析和特征提取方面，MMP结合了全局信息最大化和局部结构保持的优点。MMP 具有非线性算法的许多特性，例如 LLE和 LE算法，并且能够揭示给定数据集的全局和局部结构。更重要的是，MMP 是一种线性降维技术，使得 MMP 在实际应用中相对容易。在传统MMP算法的基础上加入时滞矩阵，使之变为具有动态特性的DMMP算法。该算法在实际工业过程中应用更为广泛，能够弥补传统故障检测算法的不足，对动态过程数据的处理起着重要作用。

2 基于动态多流形投影算法的统计过程故障检测

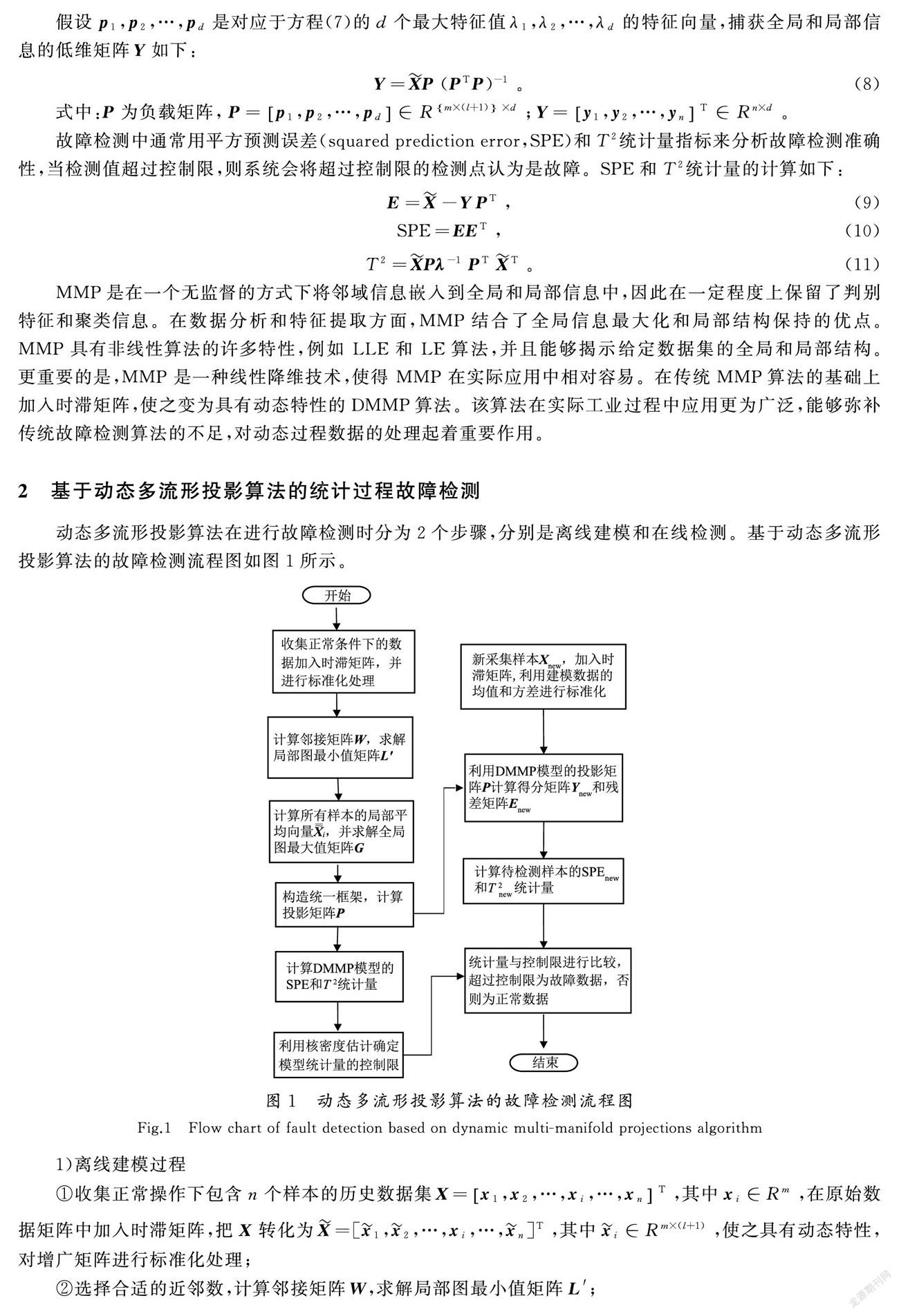
动态多流形投影算法在进行故障检测时分为2个步骤，分别是离线建模和在线检测。基于动态多流形投影算法的故障检测流程图如图1所示。

1）离线建模过程

①收集正常操作下包含n个样本的历史数据集X=x1，x2，…，xi，…，xnT，其中xi∈Rm，在原始数据矩阵中加入时滞矩阵，把X转化为X=[x1，x2，…，xi，…，xn]T，其中xi∈Rm×（l+1），使之具有动态特性，对增广矩阵进行标准化处理;

②选择合适的近邻数，计算邻接矩阵W，求解局部图最小值矩阵L′;

③计算所有样本的局部平均向量Xi，求解全局图最大值矩阵G;

④构造统一框架，求解投影矩阵p;

⑤计算DMMP模型的SPE和T2统计量;

⑥利用核密度估计确定2个统计量的控制限。

2）在线检测过程

①对新采集的样本数据Xnew，增加时滞矩阵使之扩展为具有动态特性的增广矩阵Xnew，利用建模过程数据的均值和方差对增广矩阵进行标准化处理;

②利用DMMP模型求解得到的最大化投影矩阵P计算得分矩阵Ynew和残差矩阵Enew;

③计算待检测样本的SPEnew和T2new统计量;

④将待检测样本的SPEnew和T2new与控制限进行比较，根据统计量是否超过控制限判断样本是否发生故障。

3 TE过程仿真结果与分析

3.1 TE过程

田纳西-伊斯曼（tennessee-eastman，TE）过程模拟器为一个实际的工业过程仿真平台，如今已经成为国际上通用的标准仿真模型[19-20]。

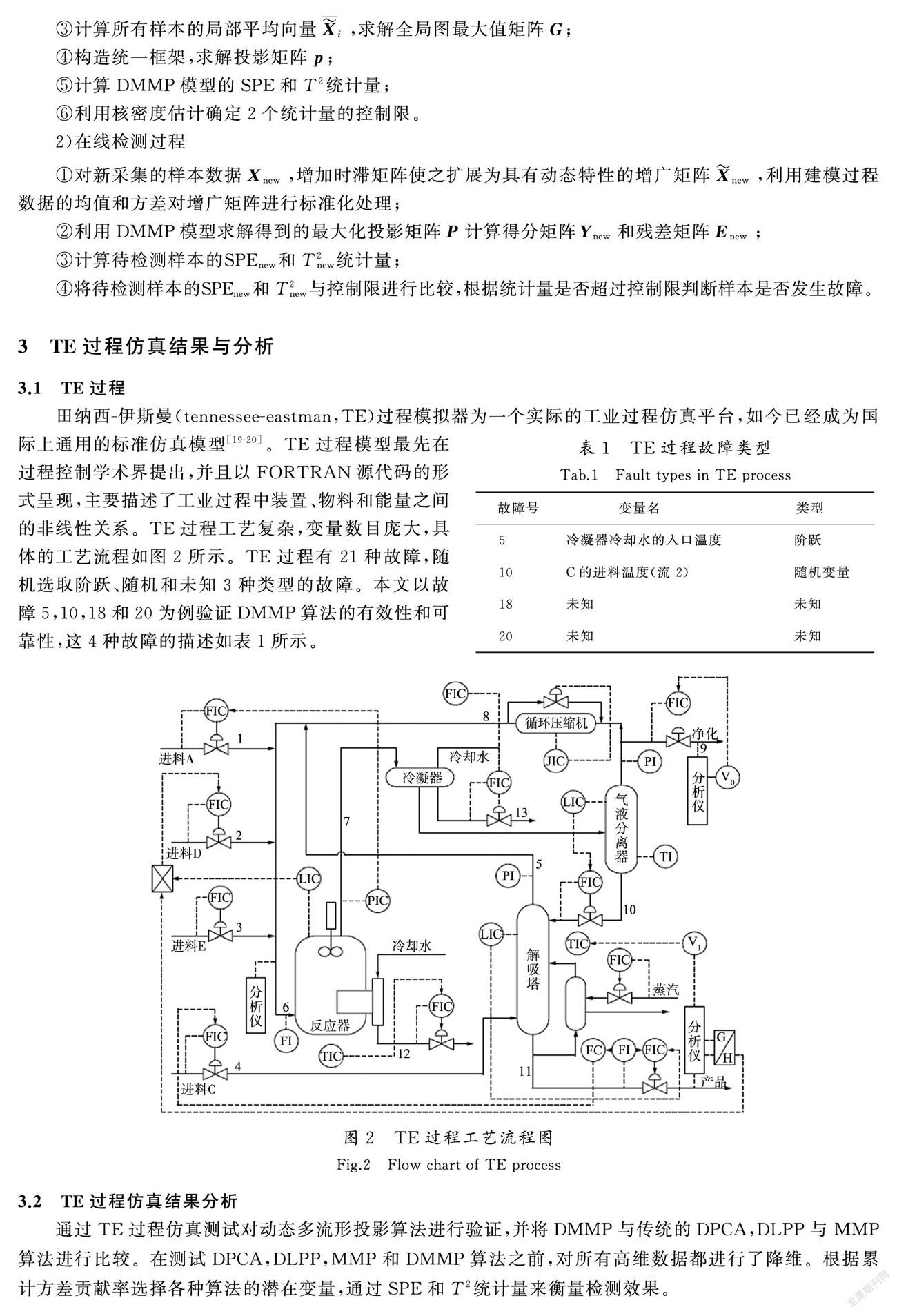
TE过程模型最先在过程控制学术界提出，并且以FORTRAN源代码的形式呈现，主要描述了工业过程中装置、物料和能量之间的非线性关系。TE过程工艺复杂，变量数目庞大，具体的工艺流程如图2所示。TE过程有21种故障，随机选取阶跃、随机和未知3种类型的故障。本文以故障5，10，18和20为例验证DMMP算法的有效性和可靠性，这4种故障的描述如表1所示。

3.2 TE过程仿真结果分析

通过TE过程仿真测试对动态多流形投影算法进行验证，并将DMMP与传统的DPCA，DLPP与 MMP算法进行比较。在测试DPCA，DLPP，MMP和DMMP算法之前，对所有高维数据都进行了降维。根据累计方差貢献率选择各种算法的潜在变量，通过SPE和T2统计量来衡量检测效果。

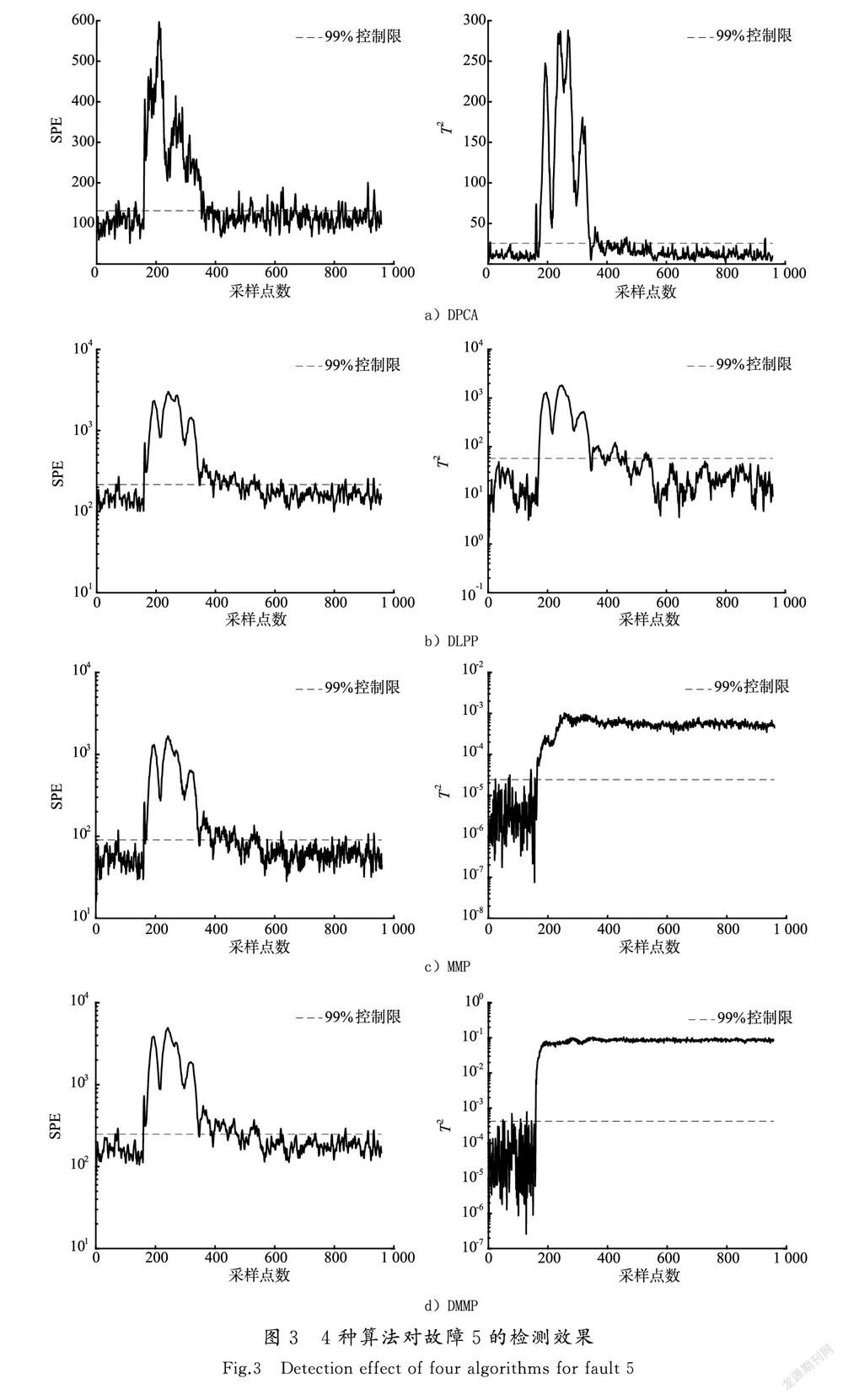
故障5为冷凝器冷却水入口温度的阶跃变化。当扰动发生时，冷凝器温度会突然升高。由于控制器的作用，扰动发生后不久冷凝器温度恢复到设定值，但冷凝器冷却水的流量异常增加，说明故障仍存在于生产过程中，需要进行故障检测。DPCA，DLPP，MMP以及DMMP 4种算法对故障5的检测结果如图3 所示。

由图3可以看出，DPCA，DLPP，MMP以及DMMP算法的SPE和T2统计量在前160个样本中都有个别样本超过控制限，产生了一定的误报，但是相比较而言，DMMP算法的2个统计量的误报率较低。TE过程的测试数据从第161时刻开始引入故障，从图3可以明显看出4种算法的SPE统计量检测效果都比较差，这是由于SPE统计量衡量的是样本向量在残差空间投影的变化，当故障发生时，故障样本向量是由与故障部分叠加的正常部分组成的，然而正常部分占比很小，所以检测效果较差。通过对比SPE统计量的故障检测率可知，DMMP算法对故障5的检测效果最好，比DPCA，DLPP和MMP算法的检测率都要高。对比4种算法的T2统计量，从图3可以明显看出DPCA和DLPP算法的检测效果很差，很难检测出故障。这是由于DPCA算法忽略了样本的局部信息造成的，而DLPP算法丢失了样本的方差信息，所以2种算法的样本主元空间的信息不全面，导致检测效果较差。与DPCA和DLPP相比，MMP算法较好，检测率高达99.63%，但是也没有完全检测出所有的故障。与DPCA，DLPP和MMP算法相比，DMMP算法的T2统计量检测效果非常好，并且检测率达到了100%，能够完全检测出所有的故障。这是因为T2统计量衡量的是样本向量在主元空间的变化，DMMP算法将邻域结构嵌入到样本数据的全局和局部结构中，保证了数据结构的完整性，使得故障检测的信息较为全面，从而检测效果最佳。故障5是一种阶跃型故障，利用传统检测算法对其检测的效果不理想，但是DMMP算法能够通过T2统计量检测出全部的故障，而且SPE统计量的检测效果比DPCA，DLPP和MMP要好。综上所述，DMMP算法对故障5的检测效果更好，验证了该算法的有效性与可靠性。

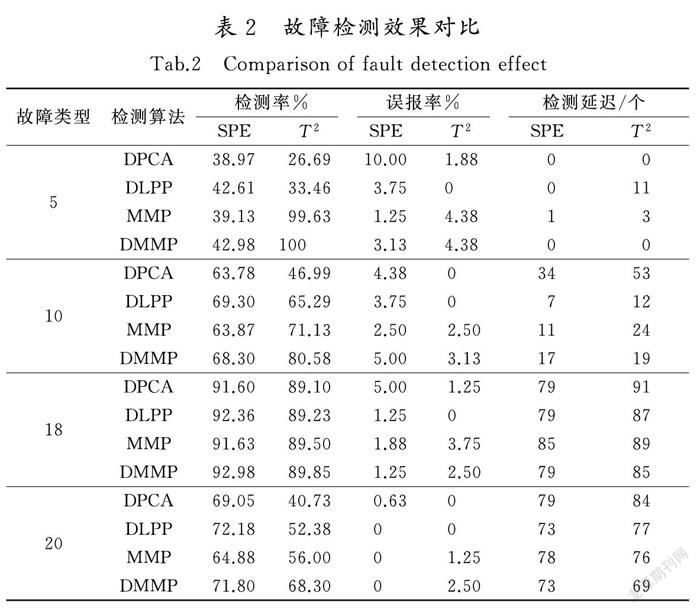
本文通过使用960个正常数据样本分别建立DPCA，DLPP，MMP 和 DMMP 4种算法的监测模型，并利用故障5，10，18和20的测试数据集对4种监测模型进行性能评价。通过对比4种算法的故障检测率、误报率和检测延迟，验证本文算法的有效性和可靠性。表2是故障检测效果对比情况，从表2可以看出本文算法的检测效果明显优于其他3种传统算法，例如故障5的T2统计量检测效果较为突出，达到100%。测试数据在第161时刻开始出现故障，检测延迟衡量的是延迟检测到故障数据的时刻。根据表2可以清楚地看到本文算法的检测延迟相对较低，也证明了本文算法的优越性。

4 结 论

本文提出一种基于动态多流形投影的多元统计过程监测新算法。在原始矩阵的基础上增加了一个时滞矩阵，使采集的数据具有动态特性。在图形嵌入式学习框架下，为了利用包含采样数据全局和局部信息的潜在的几何结构，传统的MMP算法设计全局图和局部图分别刻画全局和局部结构。通过全局图最大值和局部图最小值矩阵构造了一对对偶函数，形成统一框架。利用图的嵌入能力，將数据的邻域结构嵌入到局部和全局信息中，然后计算局部图最小值矩阵以及全局图最大值矩阵，再求解多流形投影的最大化投影矩阵。通过捕获全局和局部信息的低维矩阵计算SPE和T2统计量，利用核密度估计确定统计量的控制限，最终将待测数据的统计量与控制限进行对比，判断数据是否故障。TE过程仿真结果表明基于DMMP的监测算法能够有效进行特征提取和降维，在故障检测中表现出良好的性能。然而DMMP是一种线性降维算法，特征提取需要线性过程变量，非线性降维问题以及将该方法推广到非线性过程的故障检测还有待进一步研究。

参考文献/References：

[1] 孔祥玉，杨治艳，罗家宇，等.基于新息矩阵的独立成分分析故障检测方法[J].中南大学学报（自然科学版），2021，52（4）：1232-1241.

KONG Xiangyu，YANG Zhiyan，LUO Jiayu，et al.Fault detection method with Independent component analysis based on innovation matrix[J].Journal of Central South University（Science and Technology），2021，52（4）：1232-1241.

[2] 李元，张昊展，唐晓初.基于多模态数据全信息的概率主成分分析故障检测研究[J].仪器仪表学报，2021，42（2）：75-85.

LI Yuan，ZHANG Haozhan，TANG Xiaochu.Study on probabilistic principal component analysis fault detection based on full information of multimodal data[J].Chinese Journal of Scientific Instrument，2021，42（2）：75-85.

[3] 朱振杰，杜付鑫，杨旺功.基于主成分分析-孪生支持向量机的工业系统故障监测[J].济南大学学报（自然科学版），2021，35（3）：253-257.

ZHU Zhenjie，DU Fuxin，YANG Wanggong.Fault monitoring of industrial systems based on principal component Analysis-Twin support vector machine[J].Journal of University of Jinan（Science and Technology），2021，35（3）：253-257.

[4] 司亚斌.基于偏最小二乘和慢特征分析的复杂过程监测研究[D].北京：北京化工大学，2020：1-80.

SI Yabin.Research on Complex Process Monitoring Based on Partial Least Squsres and Slow Feature Analysis[D].Beijing：Beijing University of Chemical Technology，2020.

[5] 楊冲，宋留，刘鸿斌.基于独立元分析的制浆造纸废水处理过程故障检测[J].中国造纸学报，2019，34（1）：66-72.

YANG Chong，SONG Liu，LIU Hongbin.Fault detection of papermaking wastewater treatment process based on Independent component analysis[J].Transactions of China Pulp and Paper，2019，34（1）：66-72.

[6] JOLLIFFE I T.Principal component analysis[J].Journal of Marketing Research，1988，25（4）.DOI：10.2307/3172953.

[7] VANHATALO E，KULAHCI M.Impact of autocorrelation on principal components and their use in statistical process control[J].Quality and Reliability Engineering International，2016，32（4）：1483-1500.

[8] MONTGOMERY D C，JENNINGS C L，KULAHCI M.Introduction to Time Series Analysis and Forecasting[M].Hoboken，New Jersey：Wiley，2015.

[9] VANHATALO E，KULAHCI M，BERGQUIST B.On the structure of dynamic principal component analysis used in statistical process monitoring[J].Chemometrics and Intelligent Laboratory Systems，2017，167：1-11.

[10]田宇.基于优化动态核主元分析的复杂工业过程故障诊断研究[D].天津：天津理工大学，2020.

TIAN Yu.Research on Fault Diagnosis of Complex Industrial Process Based on Optimized Dynamic Kernel Principal Analysis[D].Tianjin：Tianjin University of Technology，2020.

[11]HE X F，CAI D，YAN S C，et al.Neighborhood preserving embedding[C]//10th IEEE International Conference on Computer Vision （ICCV'05）：IEEE，2005：1208-1213.

[12]HU K L，YUAN J Q.Multivariate statistical process control based on multiway locality preserving projections [J].Journal of Process Control，2008，18（7/8）：797-807.

[13]ZHANG M G，GE Z Q，SONG Z H，et al.Global-local structure analysis model and its application for fault detection and identification[J].Industrial & Engineering Chemistry Research，2011，50（11）：6837-6848.

[14]TONG C D，YAN X F.Statistical process monitoring based on a multi-manifold projection algorithm[J].Chemometrics and Intelligent Laboratory Systems，2014，130：20-28.

[15]KU W F，STORER R H，GEORGAKIS C.Disturbance detection and isolation by dynamic principal component analysis[J].Chemometrics and Intelligent Laboratory Systems，1995，30（1）：179-196.

[16]ZHANG C，GUO Q X，LI Y.Fault detection method based on principal component difference associated with DPCA[J].Journal of Chemometrics，2019，33（1）.DOI：10.1002/cem.3082.

[17]张成，戴絮年，李元.基于DPCA残差互异度的故障检测与诊断方法[J/OL].自动化学报.[2020-03-24].DOI：10.16383/j.aas.c190884.

ZHANG Cheng，DAI Xunian，LI Yuan.Fault Detection and Diagnosis Based on Residual Dissimilarity in Dynamic Principal Component Analysis[J/OL].Acta Automatica Sinica.[2020-03-24].DOI：10.16383/j.aas.c190884.

[18]XU Wanjiang，LUO Can，JI Aiming，et al.Coupled locality preserving projections for cross-view gait recognition[J].Neurocomputing，2017，224：37-44.

[19]WANG J P.Research on TE process fault diagnosis based on PCA[J].International Core Journal of Engineering，2021，7（1）：467-472.

[20]WEI Y Q，WENG Z X.Research on TE process fault diagnosis method based on DBN and dropout[J].The Canadian Journal of Chemical Engineering，2020，98（6）：1293-1306.

3256501908226