钢-混凝土波形钢腹板组合梁弯扭性能研究

李运生 李孟彪 王亚萍 张彦玲

摘 要：為进一步揭示弯扭作用下钢-混凝土波形钢腹板组合梁的开裂机理和弯扭破坏模式，完成了5片试验梁在弯矩和扭矩联合作用下的弯扭性能模型试验，结合ANSYS有限元分析，给出弯扭作用下波形钢腹板组合梁开裂弯矩折减系数和开裂扭矩折减系数计算公式，以及极限弯矩和极限扭矩相关关系。结果表明：随着扭弯比增大，开裂弯矩减小，开裂扭矩增大，混凝土板斜裂缝与梁轴的夹角逐渐减小;破坏形式由正截面受弯破坏逐渐变化为以最大主拉斜裂缝开裂过大、裂缝间混凝土斜压短柱达到极限压应变为特征的受扭破坏。扭弯比k小于0.15时，极限弯矩基本不受扭矩影响;大于0.6时，极限扭矩基本不受弯矩影响;在0.15和0.6之间时，极限弯矩和极限扭矩均出现明显削弱，二者呈现单调下降的直线相关关系。针对一定扭弯比范围内的波形钢腹板组合梁，提出的开裂弯矩和开裂扭矩折减系数计算公式以及极限弯-扭关系方程，揭示了弯扭作用下混凝土板的开裂机理和弯扭破坏模式，可为研究其他扭弯比条件下的波形钢腹板组合梁弯扭性能提供参考。

关键词：复合结构;钢-混凝土波形钢腹板组合梁;弯扭性能;开裂荷载;极限荷载

中图分类号：U448.21   文献标识码：A

DOI：10.7535/hbkd.2022yx01011

收稿日期：2021-10-12;修回日期：2021-11-21;责任编辑：冯 民

基金项目：国家自然科学基金（51778377）;河北省自然科学基金（E2018210149）;石家庄铁道大学研究生创新资助项目（YC2021084， YC2021017）

第一作者简介：李运生（1970—），男，河南汝南人，教授，博士，主要从事组合结构、桥梁结构理论及应用方面的研究.

通讯作者：张彦玲教授。E-mail：06mzhang@163.com

Research on bending-torsional behaviors of steel-concrete composite beam with corrugated steel webs

LI Yunsheng1，2，LI Mengbiao1，2，WANG Yaping1，2，ZHANG Yanling1，2

（1.School of Civil Engineering，Shijiazhuang Tiedao University，Shijiazhuang，Hebei 050043，China;2.Key Lab of Roads and Railway Engineering Safety Control of Ministry of Education，Shijiazhuang Tiedao University，Shijiazhuang，Hebei 050043，China）

Abstract：To further reveal the cracking mechanism and the bending-torsional failure mode caused by the bending-torsional behaviors of the steel-concrete composite beam with corrugated steel webs，model experiments were conducted on five test beams under the combined bending-torsional load.Combined with ANSYS finite element analysis，reduction factors for both the cracking bending moment and torsional moment were proposed，and the bending-torsional correlation formula between the ultimate bending moment and torsional moment was suggested.The results show that，with the increase of the ratio of bending moment，the cracking torsional moment increases，while the cracking bending moment and the angle between the inclined crack and the longitudinal axis decrease gradually;the failure mode is changed from bending failure of normal section to torsional failure which is characterized by a main inclined crack and the inclined compressed concrete column reaching to the ultimate strain.When the torsional bending ratio k≤0.15，the torsional moment has little influence on the ultimate bending moment;when k≥0.6，the bending moment has little influence on the ultimate torsional moment;when 0.15<k<0.6，both the ultimate bending moment and the torsional moment are reduced apparently by the combined bending-torsional effect with a monotone decreasing linear correlation.The experimental study can reveal the interaction between the bending and torsional properties of composite beams with corrugated steel webs in a certain range of k，which reveals the cracking mechanism and bending torsion failure mode of concrete slabs under bending and torsion，provides some reference for the study of the bending and torsional properties of composite beams with corrugated steel webs in other range of k.

Keywords：

composite structure;steel-concrete composite beam with corrugated steel webs;bending-torsional behavior;cracking load;ultimate load

波形钢腹板组合梁桥具有预应力效率高、自重轻、建筑高度低、钢腹板抗屈曲性能好等优点，同时波形钢腹板施工方便，拼装条件好，具有良好的三维挠曲特性，在宽桥面桥梁和曲线桥梁中都非常适用，但也会由于宽桥的活载大偏心和曲梁梁轴曲率的影响产生复合弯扭作用。

根据对国内外相关资料的调查，发现目前针对该类型结构的抗剪性能[1-2]、抗弯性能[3-5]和抗扭性能[6-9]均已有较多研究成果，但有关波形钢腹板组合梁复合弯扭性能的成果还较少。李宏江等[10]通过空间有限元，对波形钢腹板箱梁偏载下的力学性能进行了研究，分析了高跨比、宽跨比、钢腹板的波纹形状及板厚等對其弯扭性能的影响;HU等 [11]分析了连续曲线波形钢腹板组合梁剪力滞效应的特征，并对有效分布宽度进行了研究;杨丙文[12]推导了波形钢腹板曲线箱梁的约束扭转效应及箱梁角点畸变翘曲率表达式及畸变控制微分方程;丁勇等[13]采用缩尺模型试验方法，对2根对称配筋的波形钢腹板直线PC组合梁进行了弯扭复合作用下的抗扭强度研究;仝波[14]在考虑竖向挠曲、腹板剪切、扭转和外荷载情形下，推导了波形钢腹板曲线梁桥的弯扭耦合表达式;SUNG等[15]对一座波形钢腹板PC曲线组合梁桥进行了现场静载试验和动力测试，给出了桥梁状态的安全阈值;LUKIN等[16]针对不同的钢腹板波形，采用符拉索夫薄壁杆理论，对2点偏心加载的波形钢腹板梁的弯扭性能进行了理论分析，但只限于弹性阶段;李剑锋[17]对考虑扭转与畸变效应的波形钢腹板组合箱梁的抗弯承载力进行了研究。

根据以上的研究现状可以看出，虽然目前针对波形钢腹板直梁的偏心扭转和曲梁的弯扭耦合已有部分研究，但大部分是采用数值或理论分析，关于波形钢腹板组合梁弯扭性能的试验数据还较少，对其弯扭相互作用机理和弯扭相关关系等的研究还不够系统和深入。鉴于此，本文通过5片波形钢腹板预应力直线组合梁在弯矩与扭矩联合作用下的全过程模型试验，结合数值分析和理论推导，对弯扭破坏形态以及开裂弯矩和开裂扭矩、极限弯矩和极限扭矩的相互关系进行研究。

1 模型试验

1.1 试验设计

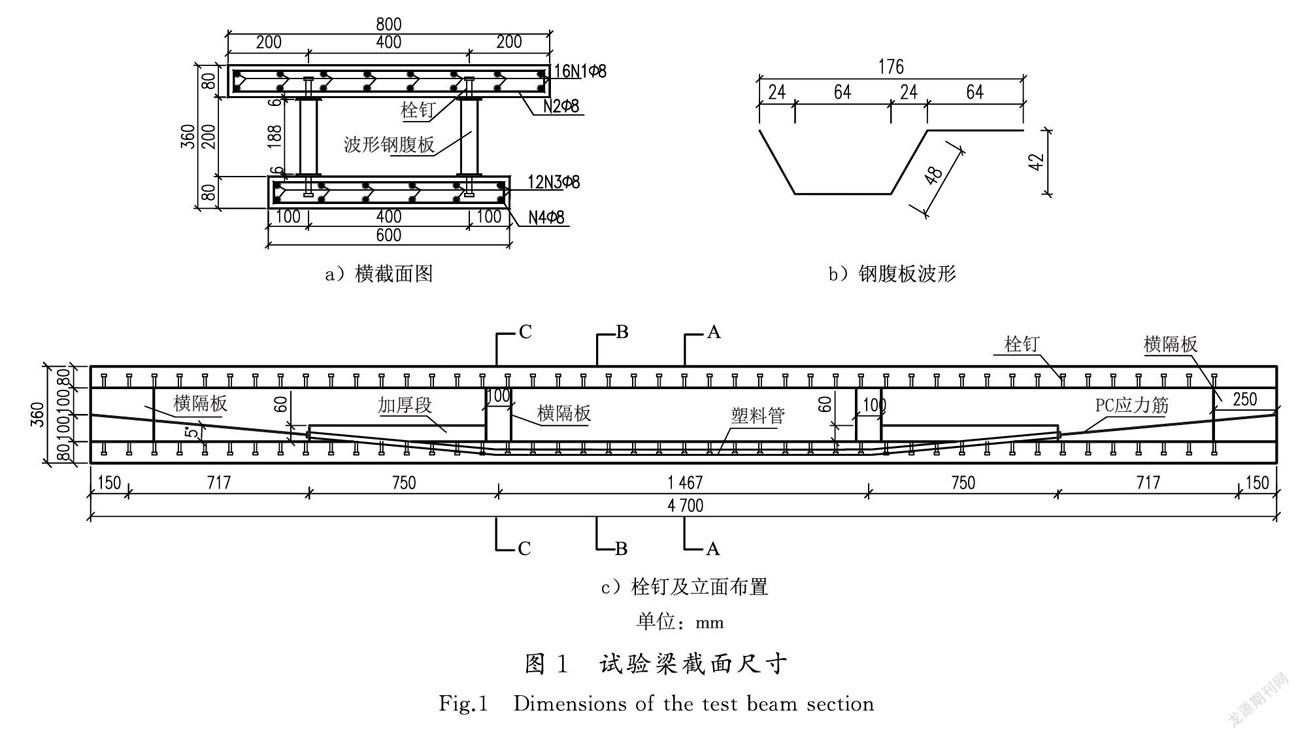
设计了5片试验梁，其中2片分别进行纯弯（SB）和纯扭试验（ST），3片进行弯扭试验。根据所施加的扭矩T与弯矩M的比值（扭弯比k=T/M），弯扭试验梁的扭弯比k分别为0.1（SBT1）、0.2（SBT2）和0.4（SBT3）。各试验梁的截面形式及尺寸、计算跨径、材料和配筋形式完全相同，均为单箱单室简支箱梁，总跨径4.7 m，计算跨径4.4 m，梁高0.36 m。在2个梁端和2个三分点处共设置了4个横隔板，其中中横隔板厚0.1 m，端横隔板厚0.25 m。在箱室内均匀地布置了2束7Φ5的钢绞线，每束截面直径为15.2 mm。主筋及箍筋经计算均采用Φ8 mm钢筋。试验梁截面尺寸及几何尺寸分别见图1和表1。

1.2 试验梁材料特性及性能试验

试验梁顶、底板及横隔板混凝土均为C40，波形钢腹板采用Q235，普通钢筋均采用HRB400。通过材料性能试验得到：混凝土立方体抗压强度标准值为49.57 MPa，弹性模量Ec=3.5×104 MPa;纵向钢筋及箍筋屈服强度为495.59 MPa，极限抗拉强度为659.88 MPa;3 mm厚波形钢腹板的屈服强度为320.59 MPa，极限抗拉强度为454.74 MPa;6 mm厚波形钢腹板上、下翼缘屈服强度为438.95 MPa，极限抗拉强度为504.82 MPa。预应力筋抗拉强度等级为1 860 MPa。

1.3 加载方案

试验加载方案为在波形钢腹板简支直线组合梁上同步施加弯矩和扭矩。采用液压伺服试验机进行三分点竖向加载获得跨中区域的纯弯段（见图2 a）、图2 b））;通过在梁端张拉钢绞线的方式对加载横梁施加偏心竖向力获得扭矩（见图2 c））。试验梁的支承方式纵向为简支，一端为固定铰支座（见图2 d）），另一端为活动铰支座（见图2 e））。在固定铰端反力架下方放置1个纵向的铰支座（见图2 f）），使反力架及梁整体可以绕梁轴转动，从而通过千斤顶施加偏心竖向力以获得扭矩。

对纯弯梁SB，撤掉固定端的纵向铰，只进行三分点竖向加载;对纯扭梁ST，撤掉纵向的固定和活动铰支座，一端固定，另一端设纵向铰并施加扭矩;弯扭梁SBT1，SBT2，SBT3则分别按扭弯比0.1，0.2和0.4同步施加弯矩和扭矩。每片梁预应力筋的初始张拉力均为100 kN。采用分级加载制度，每级加载20 kN，在开裂荷载附近荷载等级加密，屈服后改为位移加载。

1.4 测点布置

每片梁选取2个纯弯段内的截面进行测试：A截面为跨中截面，B截面距跨中约375 mm，是A截面的补充截面，其上的钢筋测点减半。除钢筋外，混凝土板和钢梁腹板上均采用应变花。在跨中截面A和预应力筋起弯点截面C处共放置6个竖向位移计。截面A，B，C的位置见图1 c），测点布置如图3所示。

2 有限元模型

采用ANSYS有限元软件建立了试验梁的有限元模型。混凝土顶、底板及横隔板采用Solid65单元，波形钢腹板采用Shell43单元，预应力筋采用Link8单元，预应力通过初应变法来施加。钢腹板与混凝土顶底板之间的抗剪连接件栓钉采用Combin39模拟。为了方便模型的收敛，建立了反力架模型，其中反力架采用Solid45单元进行模拟。

混凝土单轴受压应力-应变关系采用MKIN多线性随动强化模型。上升段采用GB 50010—2002推荐公式，下降段采用Hongnestad公式，如式（1）、式（2）所示：

σc=fc1-1-εc/ε02， εc≤ε0，（1）

σc=fc1-0.15εc-ε0/εcu-ε0， ε0<εc≤εcu ，（2）

式中： fc为混凝土轴心抗压强度;εc，σc分别为混凝土受压应力-应变关系曲线任一点的应变和应力值;ε0，εcu分别为混凝土受压应力-应变关系曲线的峰值压应变（0.002）和极限压应变（0.003 3）。

混凝土受拉的本构关系曲线同样采用MKIN材料模型来定义[9]，如式（3）、式（4）所示。

σts=Ecεts， εts≤εcr，（3）

σts=fcrεcr/εts0.4， εts>εcr，（4）

式中：εts，σts分别为混凝土受拉应力-应变关系曲线任一点的应变和应力值;Ec为混凝土弹性模量，取值为5 620（fc’）0.5，fc’为混凝土圆柱体抗压强度，取值为0.79fcu，k，fcu，k为混凝土立方体试件抗压强度;fcr為混凝土受拉断裂点拉应力，取值Ecεcr;εcr为混凝土受拉断裂点拉应变，取值0.000 115。

钢腹板、普通钢筋和预应力筋本构模型均采用双线性等向强化模型BISO。

有限元模型中施加的边界条件为一端活动铰支座，在图2 d）所示实际活动铰支座上垫板范围内约束高度y方向和宽度z方向的自由度，另一端为固定铰支座。固定铰支座端有反力架，因此在反力架下方约束x（纵向）、y和z 3个方向的平动自由度和绕y轴的转动自由度，这样在固定铰支座端梁就可与反力架一起绕z轴发生转动，并且满足简支梁固定铰支座的边界条件。在三分点截面顶板中间施加竖向集中力用来施加弯矩荷载，在反力架一侧施加一个向下的集中力用以产生扭矩荷载。有限元模型如图4所示。

取各梁跨中截面3号和4号位移计平均值作为平均挠度，将二者差值除以其水平间距作为扭转角，可得各梁弯矩-挠度和扭矩-扭率曲线实测值，其与有限元计算结果的对比见图5。

由图5可知，实测结果和有限元数值模拟结果吻合良好，可采用有限元模型对实测结果进行校核和补充分析。

3 弯扭受力性能分析

3.1 全过程弯扭受力特征

各试验梁的弯矩-挠度曲线与扭矩-扭率曲线实测值的对比见图6。

由图6可知：1）由于各试验梁具有相同的抗弯刚度和跨度，因此在混凝土开裂之前，弯矩-挠度曲线基本重合。开裂弯矩随扭弯比的增大而减小，扭弯比最大的SBT3开裂弯矩最小，抗弯刚度先是由于混凝土开裂而减小，弯矩-挠度曲线变缓，偏离其他未开裂梁的曲线，其后SBT2，SBT1和SB分别因达到开裂弯矩使曲线斜率依次减小。总体来说，不同扭弯比下各梁的弯矩-挠度曲线相差不大，截面开裂并未对宏观挠度造成明显影响，但极限弯矩和极限挠度随扭弯比的增大而下降。2）开裂之前扭矩-扭率曲线基本重合。开裂扭矩随扭弯比的增大而增大，开裂后截面抗扭刚度下降，扭矩-扭率曲线的斜率依扭弯比从小到大而依次减小。与弯矩-挠度曲线不同的是，各梁在开裂之后扭矩-扭率曲线出现了较大差别，说明斜裂缝的产生对截面抗扭刚度的影响比对抗弯刚度的影响更大。

3.2 裂缝特征

不同扭弯比下，各试验梁的裂缝特征也有明显区别，如图7所示。

图7中，σ为混凝土板下表面任意单元上的正应力;τ为水平剪应力;σ1为主拉应力。由图7可以看出：1）纯弯梁SB在纯弯矩区只有弯矩产生的正应变，因此主拉应力方向与梁轴平行，受拉裂缝始终与梁轴近似呈90°垂直（见图7 a））;2）纯扭梁ST在约束扭转作用下产生扭转剪应力和翘曲正应力，但后者较小，因此ST梁主要表现为扭转变形，主拉应力方向与梁轴基本呈45°，斜裂缝始终与梁轴呈40°～48°，在45°附近（见图7 e））;3）弯扭梁均首先在跨中混凝土底板底面与侧面发生开裂，裂缝发展稳定后，扭弯比为0.1的SBT1梁以斜裂缝为主，夹杂少量垂直裂缝，斜裂缝与梁轴的夹角大部分在50°～73°之间，平均在65°左右（见图7 b））;扭弯比为0.2和0.4的SBT2和SBT3梁均全部呈现为斜裂缝，SBT2斜裂缝与梁轴的夹角在50°～70°之间，平均在60°左右（见图7 c）），SBT3在45°～55°之间，平均在50°左右（见图7 d））;除纯弯梁SB之外，其他各试验梁在破坏之前均在支座处产生了较宽的受扭斜裂缝（见图7 f））。弯扭梁SBT1，SBT2和SBT3在弯矩和扭矩的共同作用下，受拉区同时产生弯矩下的拉应力和扭矩下的水平剪应力，使主拉应力与梁轴不再平行，受拉裂缝由纯弯时的垂直裂缝变为斜裂缝。根据弯扭区混凝土底板应变花的测点数据，开裂前3片弯扭梁底板下表面主拉应变与梁轴的夹角α如表2所示。

斜裂缝角度近似与主拉应变的方向垂直，因此根据表2主拉应变的方向可以得到3片试验梁斜裂缝与梁轴的夹角分别为64°，58°和48°，这与图7中实测的斜裂缝角度变化区间比较吻合。试验结果显示，在弯扭联合作用下，斜裂缝与梁轴的夹角介于纯弯和纯扭作用之间，且随着扭弯比的增加而逐渐减小，显示了由弯曲受力状态向扭转受力状态的逐渐转变。

3.3 弯扭破坏特征

随扭弯比的增大，试验梁的极限荷载减小。纯弯梁SB和扭弯比为0.1的SBT1梁在极限状态时受拉区钢筋大面积屈服，受压区混凝土达到极限压应变被压碎，发生明显的弯曲变形，SBT1梁在扭矩加载端产生扭转角，但扭转变形较小，总体来说均呈现正截面受弯破坏形态;扭弯比为0.2的SBT2梁破坏时也主要以弯曲变形为主，但扭转变形较STB1梁明显;SBT3和ST梁最终由于混凝土板主拉裂缝过大，发生剪切破坏，梁体发生明显的扭转变形，其中SBT3梁跨中产生挠度，但极限挠度小于SB，SBT1和SBT2梁。试验结果说明，随扭弯比的增大，梁体破坏从弯曲变形为主逐渐变化为扭转变形为主，出现了正截面受弯破坏—弯扭破坏—扭转破坏的转变。

4 弯扭相互作用

4.1 开裂弯矩和开裂扭矩的相互影响

梁体开裂之前处于弹性阶段，可采用叠加原理计算应力。在弯扭荷载作用下（不考虑剪力），取跨中截面受拉区底板角点处（该处应力为最不利）的混凝土单元体，其应力状态为平面应力状态，如图7 b）—图7 d）所示，图中正应力σ由弯曲正应力σm、扭转翘曲正应力σω与畸变翘曲正应力σdω 3部分组成，即σ=σm+σω+σdω。

1）弯曲正应力σm

在计算弯曲正应力时，需考虑预应力造成的混凝土消压现象，σm按式（5）计算。

σm=MyIz-ApσpeA0-ApσpeepyIz，（5）

式中：M为跨中截面弯矩;y为截面底板下缘到换算截面形心的距离;Iz为换算截面惯性矩;Ap为钢束截面面积;σpe为预应力筋初始张拉应力;A0为换算截面面积;ep为预应力束截面中心到换算截面形心的距离。

由本文试验现象和文献[18—20]可知，波形钢腹板几乎不承担正应力，因此在进行弯曲效应计算时可忽略波形钢腹板。将本文相关试验梁数据代入式（5），并将弯矩M作为参数，则跨中截面底板角点处弯曲正应力σm表达式为

σm=9.049×10-8M-3.684。（6）

2）刚性扭转效应

刚性扭矩效应包括刚性扭转翘曲正应力σω、自由扭转剪应力τ0和约束扭转附加剪应力τω，其中τω很小，可忽略不计。根据乌氏第二理论，刚性扭转翘曲正应力σω可按式（7）计算：

σω=Bl’s/Ivs，（7）

式中：Bl为约束扭转双力矩，可采用初参数法求得;’s为广义扇性坐标;Ivs为主扇性惯性矩。

扭转剪应力τ0按式（8）计算：

τ0=T/tΩ，（8）

式中：T为跨中截面扭矩;t为箱梁混凝土底板厚度;Ω为箱梁中心线所围成面积的2倍。

将本文相关试验梁数据代入式（7）和式（8），并将扭矩T作为参数，可得跨中截面受拉区底板角点处的扭转翘曲正应力σω和扭转剪应力τ0的表达式分别为

σω=5.9×10-7T，（9）

τ=7.22×10-8T。（10）

3）畸变效应

畸变效应包括纵向畸变翘曲正应力σdω、剪应力和横向畸变应力，其中畸变剪应力数值较小，本文也忽略不计;对横向畸变应力不作研究。

纵向畸变翘曲正应力为

σdω=BdK4/JA，（11）

式中：Bd为截面畸变双力矩，可采用弹性地基梁法求解;JA为畸变翘曲惯性矩;K4为与箱形截面尺寸有关的常数。

将本文相关试验梁数据代入式（11），并将扭矩T作为参数，可得跨中截面受拉区底板角点处的畸变翘曲正应力σdω表达式为

σdω=5.98×10-8T。（12）

4）开裂荷载

由式（6）、式（9）、式（10）和式（12）可得：

σ=σm+σω+σdω=9×10-8M+1.5×10-7T-3.684，（13）

τ=τ0=7.22×10-8T，（14）

故主拉应力为

σ1=σ2+12σ2+4τ2。（15）

以上各式中，弯矩和扭矩的单位均为N·mm，尺寸单位均为mm，应力单位均为MPa。

混凝土在主拉应变达到极限拉应变时发生开裂，但混凝土极限拉应变的取值区间较大，为简化分析，本文直接取混凝土主拉应力达到其极限抗拉强度fcr为开裂条件。将式（13）、式（14）代入式（15），并令σ1等于fcr（根据式（4），本文取fcr=Ecεcr =4.08 MPa），在已知扭弯比时，即可得到开裂弯矩与开裂扭矩，其与试验值和有限元值的对比见表3。

由以上分析可知，理论计算结果与试验值和有限元值比较吻合，但弯扭共同作用下截面某一点的应力计算过程比较繁琐，而纯弯下的应力计算则较为简单，如果能将扭矩对开裂弯矩的影响采用一个折减系数来表示，则可简化计算过程。在一般的直线桥和曲线半径较小的曲线桥中，扭矩主要由活载偏心造成，通常扭弯比较小，构件以弯曲受力为主，此时只需关心扭矩对开裂弯矩的影响，因此定义开裂弯矩折减系数ηMcr= Mcr/Mcr，0，其中Mcr，0为纯弯作用下开裂弯矩值，计算方法见文献[18]。

而对于曲线半径较大的曲线桥，在梁轴曲率和活载偏心的共同作用下，会出现扭弯比较大、构件以扭转受力为主的情况，则需要关注弯矩对开裂扭矩的影响，故定义开裂扭矩折减系数ηTcr=Tcr/Tcr，0，其中Tcr，0为纯扭作用下的开裂扭矩值，计算方法见文献[19]。

弯矩折减系数ηMcr和扭矩折减系数ηTcr随扭弯比k的变化如图8所示。

由图8可知，随扭弯比的增大，开裂弯矩减小，开裂扭矩增大。但图8只是在同一种截面参数下的计算结果，以变化截面的弯扭刚度比r=EI/GId、混凝土頂底板的厚度、配筋力比和预应力筋初始应力，分析这4种参数对开裂荷载折减系数的影响，由于ηMcr和ηTcr呈明显的负相关关系，因此只对ηMcr进行分析，结果见图9。

由图9可知，仅有弯扭刚度比对不同扭弯比下的开裂弯矩折减系数有较大影响，其他参数均影响不大。考虑弯扭刚度比r的影响，对弯矩折减系数ηMcr和扭矩折减系数ηTcr随扭弯比k的变化曲线进行拟合，得到的拟合公式如式（16）、式（17）所示。

ηMcr=0.746e-2.169k+0.002r+0.219，（16）

ηTcr=-0.754e-2.639k+0.001r+0.756。（17）

4.2 极限弯矩和极限扭矩的弯扭相关关系

基于试验梁模型，采用有限元模型补充扭弯比工况，得到不同扭弯比下弯扭梁的极限弯矩Mu和极限扭矩Tu，二者的相关关系曲线如图10所示，相关关系方程如式（18）所示，其中，Mu，0为纯弯作用下的极限弯矩，计算方法见文献[18];Tu，0为纯扭作用下的极限扭矩，计算方法见文献[19]。

Tu/Tu，0=1， k≥0.6，Tu/Tu，0=-1.67Mu/Mu，0+2.023， 0.15<k<0.6，Mu/Mu，0=1， k≤0.15。（18）

由圖10与式（18）可知：波形钢腹板组合梁在弯扭作用下，当外荷载扭弯比小于0.15时，其极限弯矩与纯弯受力作用下的极限弯矩基本相同，扭矩对极限弯矩基本不产生影响;当外荷载扭弯比大于0.6后，极限扭矩与纯扭受力作用下的极限扭矩基本相同，弯矩对极限扭矩的影响也很小;而当外荷载扭弯比在0.15～0.6之间时，极限弯矩与极限扭矩则均小于单一受力状态下的极限荷载，扭矩对抗弯强度的削弱及弯矩对抗扭强度的削弱作用较为明显，极限弯矩和极限扭矩呈单调下降的直线相关关系。

5 结 论

本文完成了5片波形钢腹板组合梁在弯矩和扭矩联合作用下的弯扭性能模型试验，揭示了弯扭作用下混凝土板的开裂机理和弯扭破坏模式，结合ANSYS有限元分析，给出了波形钢腹板组合梁在弯扭作用下开裂弯矩和开裂扭矩的折减系数表达式，以及弯扭相关关系方程，主要结论如下。

1）不同扭弯比下各梁的弯矩-挠度曲线相差不大，截面开裂并未对宏观挠度造成明显影响，但使扭矩-扭率曲线出现了较大差别，说明斜裂缝的产生对截面抗扭刚度的影响比对抗弯刚度的影响更大。

2）随着扭弯比的增大，混凝土斜裂缝与梁轴的夹角逐渐减小;破坏形式由受拉钢筋屈服、受压区混凝土达到极限压应变的正截面抗弯破坏模式逐渐变化为最大主拉斜裂缝开裂过大、裂缝间混凝土斜压短柱达到极限压应变的弯扭破坏模式，显示了由弯曲受力状态向扭转受力状态的逐渐转变。

3）随扭弯比的增大，开裂弯矩减小，开裂扭矩增大。可采用弯矩折减系数对纯弯作用下的开裂弯矩、扭矩折减系数对纯扭作用下的开裂扭矩进行修正，得到弯扭作用下的开裂弯矩和开裂扭矩。

4）扭弯比小于0.15时，波形钢腹板组合梁极限弯矩基本不受扭矩影响;扭弯比大于0.6时，极限扭矩基本不受弯矩影响;扭弯比在0.15～0.6之间时，扭矩对抗弯强度的削弱及弯矩对抗扭强度的削弱作用较为明显，极限弯矩和极限扭矩呈单调下降的直线相关关系。

由于弯扭共同加载下的试验装置比较复杂，本文尚欠缺对于大扭弯比下波形钢腹板组合梁的弯扭性能试验研究，这是今后需要努力的方向。

参考文献/References：

[1] 陈卓异，黄侨，杨明，等.波形钢腹板组合槽型梁剪切挠度计算方法与试验研究[J].工程力学，2014，31（10）：116-122.

CHEN Zhuoyi，HUANG Qiao，YANG Ming，et al.Experimental research on and calculation of shear deflection for trough girders with corrugated steel webs[J].Engineering Mechanics，2014，31（10）：116-122.

[2] ZHOU M，LIU Z，ZHANG J D，et al.Deformation analysis of a non-prismatic beam with corrugated steel webs in the elastic stage[J].Thin-Walled Structures，2016，109：260-270.

[3] LEE D H，OH J Y，KANG H，et al.Structural performance of prestressed composite girders with corrugated steel plate webs[J].Journal of Constructional Steel Research，2015，104：9-21.

[4] 刘晓刚，聂鑫，樊健生.波形钢腹板组合梁无黏结预应力筋应力增量研究[J].建筑结构学报，2014，35（10）：47-55.

LIU Xiaogang，NIE Xin，FAN Jiansheng.Research on prestressing tendons stress increment of prestressed composite beams with corrugated webs[J].Journal of Building Structures，2014，35（10）：47-55.

[5] 周勇超，郝宪武，李子青.变截面波形钢腹板组合梁剪力滞效应[J].长安大学学报（自然科学版），2014，34（4）：62-69.

ZHOU Yongchao，HAO Xianwu，LI Ziqing.Shear lag effect of non-uniform composite beam with corrugated steel web[J].Journal of Chang'an University（Natural Science Edition），2014，34（4）：62-69.

[6] 刘保东，冯文章，任红伟，等.波纹钢腹板连续刚构桥扭转与畸变的试验研究[J].中国铁道科学，2015，36（4）：40-46.

LIU Baodong，FENG Wenzhang，REN Hongwei，et al.Experimental study on torsion and distortion of continuous rigid frame bridge with corrugated steelwebs[J].China Railway Science，2015，36（4）：40-46.

[7] DING Y，JIANG K B，LIU Y W.Nonlinear analysis for PC box-girder with corrugated steel webs under pure torsion[J].Thin-Walled Structures，2012，51：167-173.

[8] 江克斌，丁勇，杨建奎，等.波形钢腹板PC组合箱梁纯扭作用下抗扭承载力试验研究[J].工程力学，2013，30（6）：175-182.

JIANG Kebin，DING Yong，YANG Jiankui，et al.Experimental study on ultimate torsional strength of PC composite box-girder with corrugated steel webs under pure torsion[J].Engineering Mechanics，2013，30（6）：175-182.

[9] SHEN K J，WAN S，MO Y L，et al.Behavior of single-box multi-cell box-girders with corrugated steel webs under pure torsion（Part I）：Experimental and numerical studies[J].Thin-Walled Structures，2018，129：542-557.

[10]李宏江，叶见曙，万水，等.波形钢腹板箱梁偏载下的力学性能[J].交通运输工程学报，2004，4（2）：23-26.

LI Hongjiang，YE Jianshu，WAN Shui，et al.Mechanical performances of box girder with corrugated steel webs under eccentric loading[J].Journal of Traffic and Transportation Engineering，2004，4（2）：23-26.

[11]HU Z T，CHEN X.Finite element analysis on shear-lag effect in curved continuous box girder with corrugated steel webs[C]//Ninth International Conference of Chinese Transportation Professionals（ICCTP）.[S.l.]：American Society of Civil Engineers，2009：2213-2218.

[12]杨丙文.波形钢腹板PC曲线箱梁桥力学性能研究[D].南京：东南大学，2013.

YANG Bingwen.Research on Mechanical Properties of the PC Curved Box-Girder Brjdge with Corrugated Steel Webs[D].Nanjing：Southeast University，2013.

[13]丁勇，江克斌，林铸明，等.波形钢腹板PC组合箱梁弯扭复合作用下抗扭强度试验研究[C]//第23届全国结构工程学术会议论文集（第Ⅱ册）.兰州：[s.n.]，2014：26-30.

[14]仝波.波形钢腹板在曲线梁桥中的应用与研究[D].兰州：兰州交通大学，2015.

TONG Bo.The Application and Research in the Curve Girder Bridge with Corrugated Steel Webs[D].Lanzhou：Lanzhou Jiaotong Univer-sity，2015.

[15]SUNG Y C，LIN T K，CHIU Y T，et al.A bridge safety monitoring system for prestressed composite box-girder bridges with corrugated steel webs based on in-situ loading experiments and a long-term monitoring database[J].Engineering Structures，2016，126：571-585.

[16]LUKIN A A，KHOLOPOV I S，ALPATOV V Y，et al.Beams with corrugated web：Calculation peculiarities of bending torsion analysis[J].Procedia Engineering，2016，153：414-418.

[17]李劍锋.考虑扭转与畸变效应的波形钢腹板组合箱梁抗弯承载力研究[D].广州：广州大学，2016.

LI Jianfeng.Study on the Bending Bearing Capacity of Corrugated Steel Web Composite Box Girder with Considering the Effect of Torsion and Distortion[D].Guangzhou：Guangzhou University，2016.

[18]汤明鑫.波形钢腹板预应力混凝土组合梁抗弯性能研究[D].石家庄：石家庄铁道大学，2020.

TANG Mingxin.Study on Bending Performance of Prestressed Concrete Composite Beams with Corrugated Steel Webs[D].Shijiazhuang：Shijiazhuang Tiedao University，2020.

[19]张彦玲，刘宇坤，李运生.波形钢腹板组合箱梁抗扭性能的试验及理论研究[J].石家庄铁道大学学报（自然科学版），2021，34（2）：1-9.

ZHANG Yanling，LIU Yukun，LI Yunsheng.Experimental and theoretical research on torsional performance of composite box girders with corrugated steel webs[J].Journal of Shijiazhuang Tiedao University（Natural Science Edition），2021，34（2）：1-9.

[20]李侥婷，李国强，楼国彪.考虑约束组合梁与组合节点相互作用的结构火灾反应分析[J].河北科技大学学报，2011，32（5）：500-506.

LI Jiaoting，LI Guoqiang，LOU Guobiao.Analysis of interaction of flush endplate composite joint and restrained composite beam in fire[J].Journal of Hebei University of Science and Technology，2011，32（5）：500-506.

3613500338247