基于单步加权最小二乘的战场集结定位算法

赵玉超 袁宏拓 孙铭

摘 要：針对目前典型的非合作区域内，如空降兵战场集结情况下，快速、高精度、低成本定位难以同时满足的问题，基于无源时差定位技术，结合实际布站和连续定位等特点，提出了一种单步加权最小二乘算法。根据时差定位技术的特点，在区域网分布式无线通信过程中，记录通信方到达各个基站的时间戳，得到时差信息，首次定位时进行两步加权最小二乘，非首次定位时利用上一次定位结果先验信息作为本次定位输入，将两步加权最小二乘简化为单步加权最小二乘。结果表明，在固定布站和随机布站情况下，6站到8站是布站资源消耗和定位精度相结合下较优的布站选择，通过相较于其他算法，新算法在-10～-20 dB信噪比下，均有较好的定位精度。故所提算法在特殊场景下能够实现较为快速、准确的定位，在随机布站时也有较好的性能，为降低算法在实际应用过程中的复杂度提供了参考。

关键词：无线通信技术;TDOA;士兵集结;Chan算法;TS-WLS

中图分类号：TN925   文献标识码：A

DOI：10.7535/hbkd.2022yx01005

收稿日期：2021-10-04;修回日期：2021-11-17;责任编辑：王淑霞

基金项目：国防科技重点实验室课题（6142205190401）

第一作者简介：赵玉超（1987—），男，河北石家庄人，高级工程师，硕士，主要从事无线自组网通信、通信导航一体化方面的研究。

通讯作者：袁宏拓。E-mail： 781296515@qq.com

Battlefield assembly location algorithm based on single step weighted least squares

ZHAO Yuchao1，YUAN Hongtuo2，SUN Ming1

（1.54th Research Institute of China Electronics Technology Group Corporation，Shijiazhuang，Hebei 050018，China;2.School of Information Science and Engineering，Hebei University of Science and Technology，Shijiazhuang，Hebei 050018，China）

Abstract：Aiming at the problem that fast，high-precision and low-cost positioning is difficult to meet in typical non-cooperative areas，such as the battlefield assembly of airborne troops，a single-step weighted least squares algorithm was proposed based on the passive time difference positioning technology and the characteristics of actual station positioning and continuous positioning.According to the characteristics of the time difference location technology，the communication timestamp to each base station was recorded in the process of regional network distributed wireless communication，and the jet lag information was obtained.The two-step weighted least squares was implemented at first positioning，while the last positioning result was used as a prior information for the location input，simplifying the two-step weighted least squares to one-step weighted least squares.The results show that 6 to 8 stations are better location choices with the combination of station resource consumption and location accuracy for fixed station and random station.Compared with other algorithms，the location accuracy is better when the SNR is -10 to -20 dB.In special scenarios，the algorithm can achieve fast and accurate location，and has good performance under random station，which provides a reference for reducing the complexity of the algorithm in practical application.

Keywords：

wireless communication technique;TDOA;soldier assembly;Chan algorithm;TS-WLS

在战场通信测距一体化环境中，基于到达时间差[1-4]（time difference of arrival，TDOA）的无源定位技术研究是当下的研究热点问题。

TDOA技术利用多个基站间同一信号的到达时间差作为已知条件，建立双曲线模型，进行目标位置的求解。根据目标到达基站间的时间差进行定位求解的算法有多种，如最小二乘算法，以Fang算法、解析Chan算法为代表的解析算法，该类算法虽然求解速度快、定位结果相对准确，但是存在无解区和模糊区[5]使其难以应用于工程实践。以泰勒级数展开法[6]、牛顿迭代法[7]为代表的迭代算法，虽然迭代次数少、多次迭代可以使误差收敛于一个极小值，但是泰勒级数展开法需要定位初始值并且存在不收敛的情况。

通过增加基站个数，增加求解过程中冗余信息，对其进行最小二乘求解可以消去无解、模糊解和迭代不收敛等缺点。常见的最小二乘类算法有最小二乘法、两步加权最小二乘法、约束加权最小二乘法和约束总体加权最小二乘法[8-13]。崔剑锋等[14]分析了多基站系统的误差分布特性，胡正等[15]对比了几种常用算法的定位性能。目前对TDOA算法的研究主要集中在高精度、高鲁棒性等方面[16-20]，这类算法虽然通过对误差和统计信息进行建模提高了定位精度，但同时其计算量也显著增加，在实际工程应用中，算法复杂度是必须要考虑的信息。

基于此，本文提出了一种改进的Chan算法，单步加权最小二乘法，对于低速移动物体，如士兵的连续移动，该算法将上一次迭代的位置信息加入到本次计算过程中，将原有的两步加权最小二乘算法改进只需1步加权计算的单步迭代算法，降低了算法的计算复杂度。

1 TDOA定位原理

多基站TDOA定位技术是一种依靠辐射源到不同基站间电磁波飞行到达时间差定位相对位置的一种无源定位技术，如图1所示。定位系统通常由M个基站组成，包括一个主站、M-1个副站。基站与基站间连线称为基线，其延长线称为基线延长线。基站布站可以按固定拓扑结构布站，也可以在一定范围内随机布站，不同的布站方式会影响系统的几何精度因子（geometric dilution of precision，GDOP）。

接收机在某一时刻发送一个定位请求，M个基站会在不同的时刻接收到来自接收机的定位请求。假定接收机发送定位请求的时刻为0，M个基站收到该定位请求的时刻为ti，i=0，1，…，M-1，则接收机到达M个基站的距离分别是tic，其中c是光速。每2个基站作为焦点，2个基站间到达时间差是一个固定值，这个固定值可以确定一条由2个基站作为焦点的双曲线。3个基站产生2个到达时间差，产生2条双曲线，可以在二维区域对目标进行定位。增加一个基站时，4站可以对三维空间目标进行定位。增加多个基站，可以利用产生的冗余信息，对目标进行进一步的精确定位。

设接收机坐标为（x，y，z），M个基站的坐标为（xi，yi，zi），i=0，1，…，（M-1），其中，i=0时为主站，其他基站为副站。目标到基站的距离为ri，i=0，1，…，（M-1），距离差为ri0，i=1，…，（M-1）。则TDOA的一般性表达式为

r0=（x-x0）2+（y-y0）2+（z-z0）2，ri=（x-xi）2+（y-yi）2+（z-zi）2，ri0=ri-r0=c·Δti，（1）

式中：Δti表示目标辐射源到达第i个基站与到达主基站的时间差。

2 单步加权最小二乘算法

2.1 算法推导

Chan算法有2种表现形式，一种是基站个数M等于定位维度数加1，一般是4站三维定位和3站二维定位，这种表现形式被广泛称为Chan算法;另一种是基站个数M大于定位维度数加1，利用冗余信息对定位结果进行最优求解，因为其有2步加权最小二乘，所以被称为TS-WLS算法。

本文所提算法由TS-WLS算法改进而来，针对于移动物体的连续定位，给出了优化后的计算过程。

由式（1）中第2个方程得：

r2i=（x2+y2+z2）+（x2i+y2i+z2i）+2（xix+yiy+ziz）。（2）

令：x2i+y2i+z2i=Ki，代入式（2），再将结果带入式（1），可得：

r2i-r20=（Ki-K0）-2[（xi-x0）x+（yi-y0）y+（zi-z0）z]。（3）

因：

ri0=ri-r0=c·Δti，（4）

令xi0=xi-x0，yi0=yi-y0，zi0=zi-z0，

联立式（3）和式（4）可得：

-2（xi0x+yi0y+zi0z）=r2i0+2ri0r0-Ki+K0，（5）

式中r2i0+2ri0r0=r2i-r20。

令Za=[ZTp，r0]T为未知矢量，其中Zp=[x，y，z]T，由式（5）中求出的具有TDOA噪声的误差矢量为

ψ=h-GaZa，（6）

式中：

h=12r210-x21-y21-z21+x20+y20+z20r220-x22-y22-z22+x20+y20+z20       r2i0-x2i-y2i-z2i+x20+y20+z20，（7）

Ga=-x10 y10 z10 r10x20 y20 z20 r20xi0 yi0 zi0 ri0。（8）

在此，定義无噪声时*的表达形式为*0，故Δti=Δt0i+ni，ri0=r0i0+c·ni0。又由于r0i=r0i0+r00，可得噪声的误差矢量为

ψ=c·B·n+0.5c2·n⊙n，（9）

其中，

B=diag{r01，r02，…，r0i}。

式中：⊙代表Schur乘积。当信噪比（SNR）高时，由广义互相关（GCC）检测的TDOA测量值通常为高斯数据，服从近似的正态分布，因此噪声矢量n也服从近似的正态分布，误差矢量的协方差矩阵便可算出。在实践中条件c·ni0r0i通常可以满足，因而式（9）中的第2项可以忽略，误差矢量ψ成为具有以下协方差矩阵的高斯随机矢量：

Ψ=EψψT=c2BQB，（10）

式中：Q为TDOA测量的协方差矩阵，Za中r0与式（2）有关，表明式（6）仍然是以x，y，z为变量的非线性方程组。

求解该非线性方程组时，假定x，y，z和r0之间无关，令噪声误差矢量最小，则

h=GaZa。（11）

Za的加权最小二乘解为

Za=（GTaΨ-1Ga）-1GTaΨ-1h。（12）

式（12）是式（6）的WLS解，这一步与TS-WLS的第1步相同，目前该式还不能解出，因为B中含有接收机与各测量站之间的距离，故Ψ仍然是未知量。为此，需作进一步近似。

假定接收机与各基站间距离相同，r0i（i=1，2，…，M-1）与r（定义距离）接近，故B≈r0I。由于Ψ的量纲没有什么影响，故式（12）可近似为

Za≈（GTaQ-1Ga）-1GTaQ-1h。（13）

在士兵初次定位时没有初始定位结果，式（13）可以作为第一次定位的粗略解。利用粗略解可以得到接收机到各个基站粗略的距离r0i，进而得到较第1次WLS更为精确的B，将B代入式（10），得到Ψ=E[ψψT]=c2BQB，再利用式（12）进行第2次WLS即可得到改进的TS-WLS解。

在士兵的后续连续定位中，利用上一次定位时的估计位置作为已知，求得估计值B，利用式（12），只进行一次WLS即可求得较为精确的定位结果。相比于TS-WLS的两步最小二乘算法，需要在进行第1次加权最小二乘后重新构造误差函数进行第2次最小二乘，本文所提算法在士兵的每次定位中只需要1次最小二乘计算即可求出较为精确的定位结果，其计算量远小于TS-WLS算法。

2.2 计算步骤

从整个算法的计算流程可知，TS-WLS算法在计算第1次最小二乘时，因为没有先验信息B，无法得到一个准确的加权最小二乘解。本文所提算法利用上一次定位得到的位置信息作为先验信息B带入加权最小二乘计算中，当该算法在第1次定位迭代时，采取TS-WLS算法中的方法，假设B≈r0I，求得第1次加权最小二乘解，获得一个粗略的B，将B作为已知条件再次代入第1步加权最小二乘中，获得第1次定位的准确解。

本文所提算法的核心思想是在进行本次加权最小二乘计算前，采取步进迭代方式，预先由上一次的位置信息得到本次计算所需的B，作为一个先验信息参与到本次加权最小二乘计算中，得到一个精确定位结果。

当物体进行连续移动定位时，初次定位需要进行2次最小二乘，非初次定位时，第k次定位的先验信息B由第（k-1）次的定位结果得到，在已知先验信息B的情况下，只需1步加权最小二乘即可得到准确解。

本文所提算法的流程图如图2所示，

计算步骤如下。

步骤1 通过基站得到本次时差Δti;

步骤2 将时差Δti代入式（7）和式（8），得到h和Ga;

步骤3 求得协方差矩阵Q;

步骤4 第1次定位时转步骤5，否则步骤7;

步骤5 令B≈r0I得到Ψ≈Q，将h和Ga一起代入式（13）求得粗略解;

步骤6 得到一个粗略的B，转到步骤8;

步骤7 将上一次定位结果r0i代入B，获得1个有移动误差的B;

步骤8 将B代入式（10），得到Ψ;

步骤9 利用式（12）求得本次定位精确解。

3 仿真分析

针对士兵战场环境下连续定位，本文所提算法提供了一个优化的计算过程，将TS-WLS的两步最小二乘在连续移动定位的情况下精简为单步迭代最小二乘。所提算法无论是二维平面定位还是三维空间定位都有其应用价值，二维定位去掉了高度信息，也相应去掉了高度带来的误差，计算量更小，在高度值不太重要的场合，采用二维定位会适当减小计算量和误差。本文针对士兵战场环境下定位，模拟平原、巷战、伞兵集结等作战方式进行二维平面定位分析。

3.1 固定和随机布阵下多基站性能分析

首先仿真了本文所提算法在不同基站数目下蒙特卡洛试验次数为1 000次时的均方根误差（root-mean-square error，RMSE）随信噪比（signal to noise ratio，SNR）的变化情况。定位区域为以坐标点（0，0）为中心点，正负5 000 m的正方形二维平面坐标系。时间误差模拟接收机芯片的固定延迟，取10 ns。接收机噪声为高斯白噪声，固定信号功率，改变噪声功率，使信噪比变化范围为-10～20 dB，步进量为2 dB。士兵初始位置为坐标系内（100，150）点的位置，移动速度为22m/s，vx=vy=2 m/s，定位频率为1次/s。

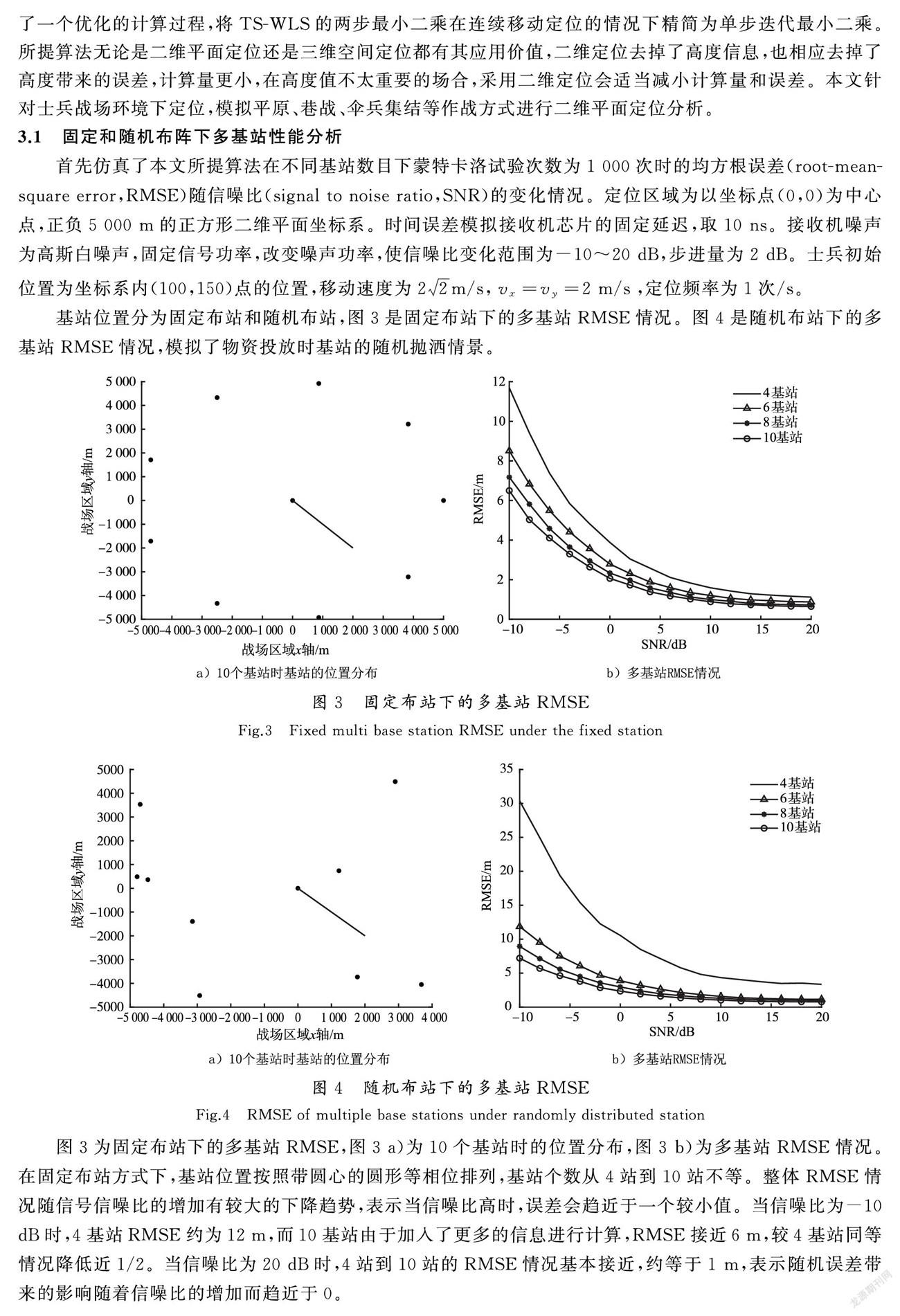
基站位置分为固定布站和随机布站，图3是固定布站下的多基站RMSE情况。图4是随机布站下的多基站RMSE情况，模拟了物资投放时基站的随机拋洒情景。

图3为固定布站下的多基站RMSE，图3 a）为10个基站时的位置分布，图3 b）为多基站RMSE情况。在固定布站方式下，基站位置按照带圆心的圆形等相位排列，基站个数从4站到10站不等。整体RMSE情况随信号信噪比的增加有较大的下降趋势，表示当信噪比高时，误差会趋近于一个较小值。当信噪比为-10 dB时，4基站RMSE约为12 m，而10基站由于加入了更多的信息进行计算，RMSE接近6 m，较4基站同等情况降低近1/2。当信噪比为20 dB时，4站到10站的RMSE情况基本接近，约等于1 m，表示随机误差带来的影响随着信噪比的增加而趋近于0。

图4所示为随机布站下的多基站RMSE，图4 a）为10个基站时的位置分布，图4 b）为多基站RMSE情况。在随机布站方式下，基站位置随机，基站个数从4站到10站不等。与固定布站不同，随机布站下4基站定位误差急剧增加，并且信噪比在20 dB时并没有收敛于一个极小值，这表明随机布站下4基站定位精度有较大的下降，这是由于随机布站的GDOP恶化严重，使得定位精度下降。当布站个数为6站到10站时，RMSE接近于固定布站情况，但是略高。

从固定布站和随机布站的多基站RMSE仿真中可以看出，固定布站因为拥有较好的GDOP，所以整体RMSE相比于随机布站要低，相同的误差环境下定位精度更高。而随机布站，因为布站具有随机性的原因，基站数目与定位精度总体呈现一定的正相关性，这是因为随着基站数目的增多，可利用的信息增多。当固定布站个数从6降为4时，本文所提算法的RMSE恶化情况相比于从8站降为6站略有提高;当随机布站个数从6降为4时，本文所提算法的RMSE恶化情况明显高于6站、8站和10站，这是由于布站个数较少，随机性强，基站GDOP较差导致的。由以上分析结果可知，不论是固定布站还是随机布站，6站到8站是布站资源消耗和定位精度相结合下较优的布站选择。

3.2 多种算法仿真比较

对LS算法、TS-WLS算法和本文所提算法3种算法进行仿真对比，基站个数为7，信噪比为-10～20 dB，步进幅度为2 dB。

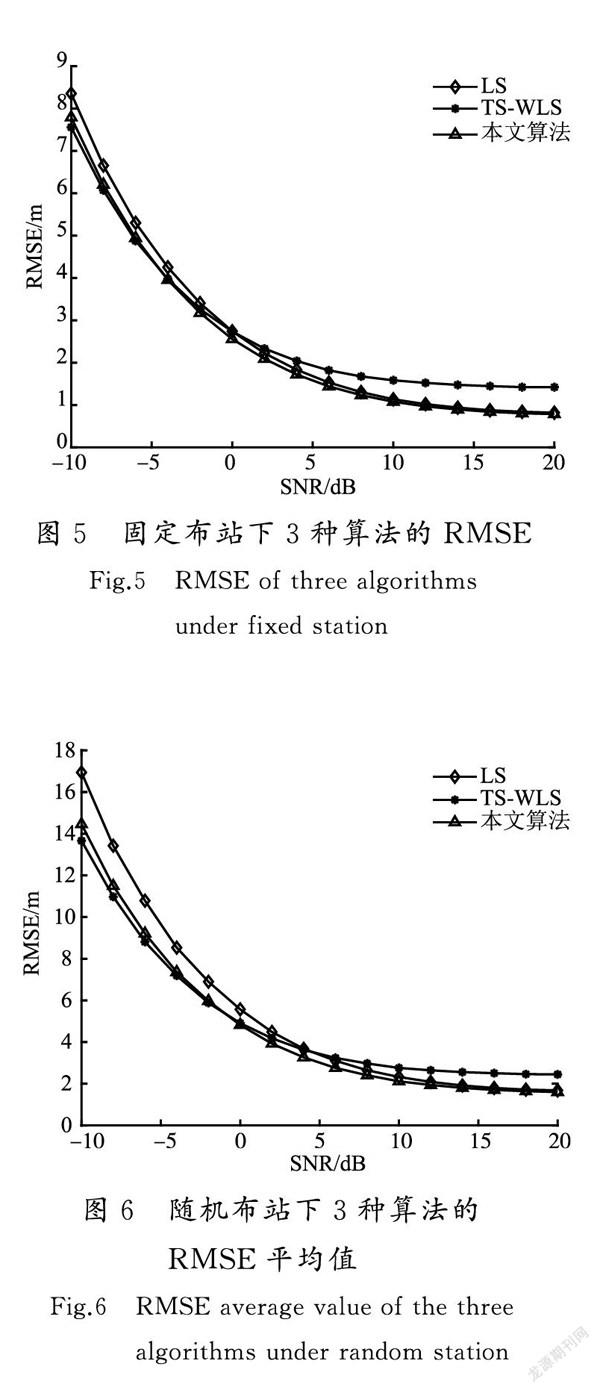
首先仿真了固定布站下3种算法的RMSE情况，图5所示为固定布站下3种算法的RMSE。

固定布站情况如前文所述，为带圆心的圆形。从图5仿真结果可以看出，当信噪比较高、信号准确性较高时，LS算法和本文所提算法的定位均方根误差较低并且相近，TS-WLS算法的均方根误差则较高，并且3种算法的均方根误差随着信号误差的减小趋于稳定。在信噪比为0 dB时，3种算法的均方根误差相近。当信噪比较低、信号准确性较差时，LS算法的均方根误差上升最大，本文所提算法的均方根误差接近并略高于TS-WLS算法，TS-WLS算法的均方根误差上升最为缓慢，在信噪比为20 dB时相比于其他2种算法为最小。

随后仿真了随机布站下3种算法的RMSE情况。随机布站时单次随机布站具有偶然性，不能说明随机布站下的实际情况，所以进行了100次随机布站，取其3种算法的RMSE平均值。

如图6所示为随机布站下3种算法的RMSE平均值所示。与固定布站方式相比，RMSE整体规律相同，数值变大。信噪比为-10 dB时，RMSE增加约8 m，信噪比为20 dB时，RMSE增加约1 m。随机布站因其固有的GDOP恶化，是定位精度较固定布站下降的主要原因。

分析上述仿真结果，在信噪比较高时LS算法有较好的定位精度。TS-WLS定位精度较低的原因是，TS-WLS算法针对噪声满足高斯误差时进行建模，在接收机含有其他噪声，如接收机钟差时，建模准确性下降，定位精度也会随之下降。LS算法没有对误差进行建模，在信噪比较高时反而有更好的定位精度。本文所提算法因为忽略了TS-WLS算法第2步加權最小二乘，迭代使用第1步加权最小二乘，在先验信息B已知的情况下，定位精度在高信噪比时也能达到较好的水平。

在信噪比较低时，LS算法因为没有对误差建模的一个过程，定位精度直接下降，均方根误差升高。TS-WLS算法因为其第二步加权最小二乘对扰动误差进行建模，在信噪比较低时，定位精度优于其他2种算法。本文所提算法由TS-WLS算法改进而来，加入了先验信息B，使第1步加权最小二乘更加精确，忽略了第2步加权最小二乘，所以在信噪比较低时，定位均方根误差接近且略高于TS-WLS算法。

4 结 论

在通信测距一体化环境中，士兵的战场定位能力是制胜关键。当战场环境存在敌方GNSS压制式干扰时，我方士兵依靠单兵装备很难进行有效的抗干扰处理。通过投放带有抗干扰能力的卫星导航接收机作为定位基站，利用TDOA技术可实现对战场环境下士兵的无源定位。

本文所提算法在信噪比较低和较高时都有着相对优秀的定位准确度，在连续定位过程中，通过不断获得前一次定位信息从而得到先验信息B，简化了单次定位的计算过程。单次定位迭代中，仅需一次加权最小二乘法就能获得相对准确的定位结果。仿真验证表明，较少的计算过程和较为准确的定位能力，使得本文所提算法对士兵战场环境下的定位具有较高的运用价值。

本文所提算法是一种连续定位解算算法，当其无法获得前一次定位中的先验信息B时，该算法退化为TS-WLS算法，计算复杂度上升。在实际应用中，将本文算法与卡尔曼滤波算法结合，将本文算法作为单次初始定位结果，利用卡尔曼滤波算法预测移动轨迹，可以进一步提高士兵的移动定位能力。

参考文献/References：

[1] HUANG Y T，BENESTY J，ELKO G W，et al.Real-time passive source localization：A practical linear-correction least-squares approach[J].IEEE Transactions on Speech and Audio Processing，2001，9（8）：943-956.

[2] LIN L X，SO H C，CHAN F K W，et al.A new constrained weighted least squares algorithm for TDOA-based localization[J].Signal Processing，2013，93（11）：2872-2878.

[3] 曲长文，王昌海，徐征.基于时差序列的多机无源定位算法研究[J].现代雷达，2013，35（3）：45-49.

QU Changwen，WANG Changhai，XU Zheng.A study on multi-plane passive location algorithm based on TDOA sequence[J].Modern Radar，2013，35（3）：45-49.

[4] 江翔.无源时差定位技术及应用研究[D].成都：电子科技大学，2008.

JIANG Xiang.Research on Passive Time Diflerence Location Technology and Ios Application[D].Sichuan：University of Electronic Science and Technology of China，2008.

[5] 王婷.无源时差定位模糊区与定位无解区研究[J].现代雷达，2017，039（11）：57-62.

WANG Ting.A Study on the Ambiguity and Non-solution Areas of Passive TDOA Location System [J].Modern Radar，2017，39（11）：57-62.

[6] 杨俊峰，张丕状.基于Chan算法和Taylor级数混合算法的到达时差定位[J].核电子学与探测技术，2013，33（4）：480-482.

YANG Junfeng，ZHANG Pizhuang.Time difference of arrival localization based on Chan algorithm andTaylor series algorithm[J].Nuclear Electronics & Detection Technology，2013，33（4）：480-482.

[7] 屈军锁，侯晓宁，张继荣，等.四基站时差和牛顿迭代法的三维定位算法[J].西安邮电大学学报，2015，20（2）：36-40.

QU Junsuo，HOU Xiaoning，ZHANG Jirong，et al.3D localization algorithm based on 4-station time difference of arrival and Newton iteration[J].Journal of Xi'an University of Posts and Telecommunications，2015，20（2）：36-40.

[8] CHAN Y T，HO K C.A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing，1994，42（8）：1905-1915.

[9] 周恭谦，杨露菁，刘忠.改进的非完全约束加权最小二乘TDOA/FDOA无源定位方法[J].系统工程與电子技术，2018，40（8）：1686-1692.

ZHOU Gongqian，YANG Lujing，LIU Zhong.Improved incomplete constrained weighted least squares TDOA/FDOA passive location method[J].Systems Engineering and Electronics，2018，40（8）：1686-1692.

[10]左燕，陈志猛，蔡立平.基于约束总体最小二乘的单站DOA/TDOA联合误差校正与定位算法[J].电子与信息学报，2019，41（6）：1317-1323.

ZUO Yan，CHEN Zhimeng，CAI Liping.Single-observer DOA/TDOA registration and passive localization based on constrained total least squares[J].Journal of Electronics & Information Technology，2019，41（6）：1317-1323.

[11]苏峰，王昌海，徐征.基于最小二乘的时差定位算法[J].雷达科学与技术，2013，11（6）：621-625.

SU Feng，WANG Changhai，XU Zheng.TDOA location algorithms based on the least squares[J].Radar Science and Technology，2013，11（6）：621-625.

[12]王领，申晓红，康玉柱，等.水声传感器网络信号到达时间差目标定位的最小二乘法估计性能[J].兵工学报，2020，41（3）：542-551.

WANG Ling，SHEN Xiaohong，KANG Yuzhu，et al.Least squares estimation performance for TDOA target localization in underwater acoustic sensor networks[J].Acta Armamentarii，2020，41（3）：542-551.

[13]CHAN Y T，YAU CHIN HANG H，CHING P C.Exact and approximate maximum likelihood localization algorithms[J].IEEE Transactions on Vehicular Technology，2006，55（1）：10-16.

[14]崔剑锋，杨宝山，杜敬林.多站式时差定位系统的误差空间分布特性[J].测试技术学报，2015，29（4）：343-347.

CUI Jianfeng，YANG Baoshan，DU Jinglin.Error space distribution character of multiple station location system[J].Journal of Test and Measurement Technology，2015，29（4）：343-347.

[15]胡正，郭立强，卜晓楠，等.多站时差定位算法的性能比较[J].现代信息科技，2019，3（15）：25-26.

HU Zheng，GUO Liqiang，BU Xiaonan，et al.The performance comparison ofmulti-station TDOA localization algorithms[J].Modern Information Technology，2019，3（15）：25-26.

[16]陈涛，王梦馨，黄湘松.基于樽海鞘群算法的无源时差定位[J].电子与信息学报，2018，40（7）：1591-1597.

CHEN Tao，WANG Mengxin，HUANG Xiangsong.Time difference of arrival passive location based on Salp swarm algorithm[J].Journal of Electronics & Information Technology，2018，40（7）：1591-1597.

[17]孔维炯，丁志中，方福柱.基于TDOA的高精度无线定位算法分析与实现[J].合肥工业大学学报（自然科学版），2019，42（6）：756-762.

KONG Weijiong，DING Zhizhong，FANG Fuzhu.Analysis and realization of high precisionradio positioning algorithm based on TDOA[J].Journal of Hefei University of Technology（Natural Science），2019，42（6）：756-762.

[18]蔡明明，王运锋.基于扩展卡尔曼滤波的时差定位算法[J].现代雷达，2020，42（4）：50-54.

CAI Mingming，WANG Yunfeng.Time difference location algorithm based on Kalman filter[J].Modern Radar，2020，42（4）：50-54.

[19]夏偉，罗明，赵美霞.无源时差定位系统最优布站方法研究[J].雷达科学与技术，2020，18（1）：34-38.

XIA Wei，LUO Ming，ZHAO Meixia.Study on optimal station distribution and performance of passive time difference localization system[J].Radar Science and Technology，2020，18（1）：34-38.

[20]IMANI S，PEIMANY M，HASANKHAN M J，et al.Bi-static target localization based on inaccurate TDOA-AOA measurements[J/OL].Signal，Image and Video Processing.[2021-07-17].DOI：10.1007/s11760-021-01985-4.

3624501908297