基于AMW-SVDD的多模态过程故障检测方法

张成 伊海迪 李元

摘 要：針对传统SVDD方法对多模态过程故障检测率低的问题，提出了自适应滑动窗口-支持向量数据描述（adaptive moving window- support vector data description，AMW-SVDD）的故障检测方法。首先，使用网格搜索方法建立窗宽序列并获取初始窗宽;其次，应用滑动窗口技术将整体数据以窗宽为标准切分到多个子窗口;然后，利用网格搜索方法和粒子群优化（particle swarm optimization，PSO）算法，得到最优窗宽和由各窗口最优SVDD模型构成的模型序列;最后，使用最优模型序列进行故障检测，并将此方法应用于数值例子及田纳西伊斯曼（TE）数据集。结果表明，与传统故障检测方法如KPCA和SVDD等相比，AMW-SVDD方法可有效捕获过程数据的多模态特性。AMW-SVDD方法通过滑动窗口技术捕获数据的局部特征，同时应用PSO算法优化局部模型，二者结合可以自适应确定窗宽参数，进一步获取最优子模型序列，能够有效解决多模态过程故障检测问题，为提高SVDD方法在多模态过程中的故障检测性能提供了参考。

关键词：自动控制技术其他学科;支持向量数据描述;粒子群优化;滑动窗口;多模态;故障检测

中图分类号：TP181;TP277   文献标识码：A

DOI：10.7535/hbkd.2022yx01001

收稿日期：2021-10-14;修回日期：2021-11-20;责任编辑： 冯 民

基金项目：国家自然科学基金（61673279）;辽宁省自然科学基金（2019-MS-262）;辽宁省教育厅基金（LJ2019013）

第一作者简介：张 成（1979—），男，辽宁沈阳人，副教授，博士，主要从事过程故障诊断分析方面的研究。

通讯作者：李 元教授。E-mail：li-yuan@mail.tsinghua.edu.cn

Multimode process fault detection method based on AMW-SVDD

ZHANG Cheng1，YI Haidi2，LI Yuan3

（1.College of Science，Shenyang University of Chemical Technology，Shenyang，Liaoning 110142，China;2.College of Computer Science and Technology，Shenyang University of Chemical Technology，Shenyang，Liaoning 110142，China;3.College of Information Engineering，Shenyang University of Chemical Technology，Shenyang，Liaoning 110142，China）

Abstract：Aiming at the problem of low fault detection rate in multimode process by traditional SVDD method，a fault detection method of support vector data description based on adaptive moving window （AMW-SVDD） was proposed.Firstly，the grid search method was used to establish the window width sequence and obtain the initial window width.Next，the moving window technology was applied to segment the overall data into multiple sub windows according to the window width.Then，the grid search method and particle swarm optimization （PSO） algorithm were used to get the optimal window width and the model sequence composed of the optimal SVDD model in each window.Finally，the optimal model sequence was used for fault detection，and this method was applied to numerical cases and Tennessee Eastman （TE） data sets.The results show that compared with traditional fault detection methods such as KPCA and SVDD，AMW-SVDD method can effectively capture the multimode characteristics of process data.In AMW-SVDD method，the local features of data are captured by moving window technology，and the local model is optimized by PSO algorithm，the combination of the two could adaptively determine the window width and further obtain the optimal model sequence，so that the problem of fault detection in multimode process can be effectively solved，which provides some reference for improving the fault detection performance of SVDD method in multimode process.

Keywords：

other disciplines of automatic control technology;support vector data description;particle swarm optimization;moving window;multimode;fault detection

隨着现代工业过程的日渐复杂化，企业对系统安全提出越来越高的要求。为了保证系统的高效运转，近年来，故障检测技术飞速发展。其中，基于数据驱动的过程监控方法可充分挖掘数据的潜在特征，逐渐成为故障诊断领域中的研究热点[1]。

在基于数据驱动的众多故障检测方法中，主元分析（principle component analysis，PCA）[2-3]、偏最小二乘（partial least squares，PLS）[4-5]及二者衍生方法的研究和应用较多[6]。这些方法可以有效处理数据中的冗余信息，降低数据维数，但过程数据中的非线性和非高斯性等特征会制约其故障检测性能[7]。而工业过程数据大多具有非线性特征，如田纳西伊斯曼（Tennessee Eastman，TE）过程[8]，连续搅拌釜（continuous stirred tank reactor，CSTR）过程[9]等。为了解决非线性过程监控问题，核技巧被引入上述方法并衍生出核主元分析（KPCA）和核偏最小二乘（KPLS）等[10-11]。其中，KPCA[12]通过核技巧使低维空间线性不可分数据映射到高维特征空间后线性可分[13-14]。需要指出的是，KPCA方法适用于非线性过程故障检测，但当过程数据具有非高斯分布特征时，该方法的故障检测性能受到制约[15]。为了解除数据必须服从高斯分布的限制，TAX等[16]提出支持向量数据描述（support vector data description，SVDD）方法。通常，该方法在单模态问题中起到重要作用，但对多模态过程监控效果有限[17-18]。为了有效监控多模态过程，多种故障检测方法被提出[19]。HE等[20]将k近邻（k nearest neighbor，KNN）算法应用到故障检测领域，提出基于KNN的故障检测方法 （fault detection using the KNN rule，FD-KNN）。ZHAO等[21]提出多PCA方法，该方法对每个模态数据建立局部模型，通过衡量不同模型间的相似性，将多模态问题转换为单模态问题进行解决。CHU等[22]结合支持向量机（support vector machine，SVM）和基于熵的变量选择方法为不同模态数据选择相应模型进行故障检测。马贺贺等[23]结合马氏距离与邻域密度特征，提出新的监控指标，使用单个模型可对多模态数据进行监控。杨雅伟等[24]通过聚类算法将不同模态切分，分别建立SVDD模型进行故障检测。值得注意的是，上述方法大多为各子模型设置统一参数，会导致部分模型无法达到最优，制约了故障检测性能。

针对多模态过程故障检测问题，本文提出了自适应滑动窗口-支持向量数据描述（SVDD based on adaptive moving window，AMW-SVDD）故障检测方法。此方法通过自适应滑动窗口技术捕获数据的局部特征，使全局具有多模态特征的数据，在各子窗内保持单模态特性。同时，应用粒子群（particle swarm optimization，PSO）[25]算法优化各子窗口模型参数，解决多子模型因统一设置参数导致的部分模型无法达到最优的问题。

1 基本算法

1.1 支持向量数据描述（SVDD）

SVDD的基本思想是寻找一个球心为a、半径为R且体积尽可能小并包含尽可能多样本的超球体。假设有一组正常训练数据H∈Rn×d，其中n为样本数，d为变量数，则SVDD原始优化问题可表述为

minR，a，ξ R2+C∑ni=1ξi，s.t. ‖Φhi-a‖2≤R2+ξi，ξi≥0， i=1，2，…，n，（1）

式中：ξi为松弛变量;C为惩罚因子。本文使用高斯核K（hi，hj）=exp（-‖hi-hj‖2σ2）代替映射后的样本间内积运算<Φ（hi），Φ（hj）>，并在引入拉格朗日乘数α=[α1，α2，...，αn]T后将式（1）转换为其对偶问题[26]：

maxα ∑ni=1αiK（hi，hi）-∑ni=1∑nj=1αiαjK（hi，hj），s.t. ∑ni=1αi=1，  0≤αi≤C。（2）

求解式（2）可以确定超球体球心a和半径R：

a=∑indexi=1αiΦ（hi），（3）

R2=K（h*，h*）-2∑indexi=1αiK（hi，h*）+∑indexi=1∑indexj=1αiαjK（hi，hj），（4）

式中：h*为支持向量;index为由支持向量所构成集合的样本数量。对于测试样本htest，其到超球体球心的距离为

D2=K（htest，htest）-2∑indexi=1αiK（hi，htest）+∑indexi=1∑indexj=1αiαjK（hi，hj）。（5）

若D>R，则为故障样本，否则为正常样本。

1.2 粒子群优化（PSO）

初始化粒子群，每个粒子有各自速度v和位置x：

vk+1id=ωvkid+c1r1（pkid，pbest-xkid）+c2r2（pkd，gbest-xkid），xk+1id=xkid+vk+1id，（6）

式中各参数含义如表1所示。

迭代过程中，通过比较x处适应值与pbest，gbest大小对当前最优解进行更新。算法具体步骤如下：

1）初始化各粒子位置x和速度v，pbest为当前位置最优解，gbest为pbest中最优值。

2）计算各粒子适应度，比较与pbest及gbest大小，更新pbest和gbest。

3）由式（6）更新各粒子速度和位置。

4）若達到最大迭代次数或者gbest达到预设阈值则停止优化，输出最优解，否则，转到步骤2）。

2 自适应滑动窗口-支持向量数据描述的故障检测方法

2.1 PSO算法寻参策略

SVDD中惩罚因子C和核函数参数σ的初始值设置是决定模型性能的最重要因素。PSO算法的使用，可以保证各子窗口SVDD模型是针对此窗口局部数据达到最优。另外，由于多数工业过程数据维数高，导致无法直接观察模型拟合情况，使得经验值调参过程变得艰难;而PSO算法通过合理设置粒子数及迭代次数，无需调参经验，自动获得最优参数，相较于经验值调参，优势会更加明显。

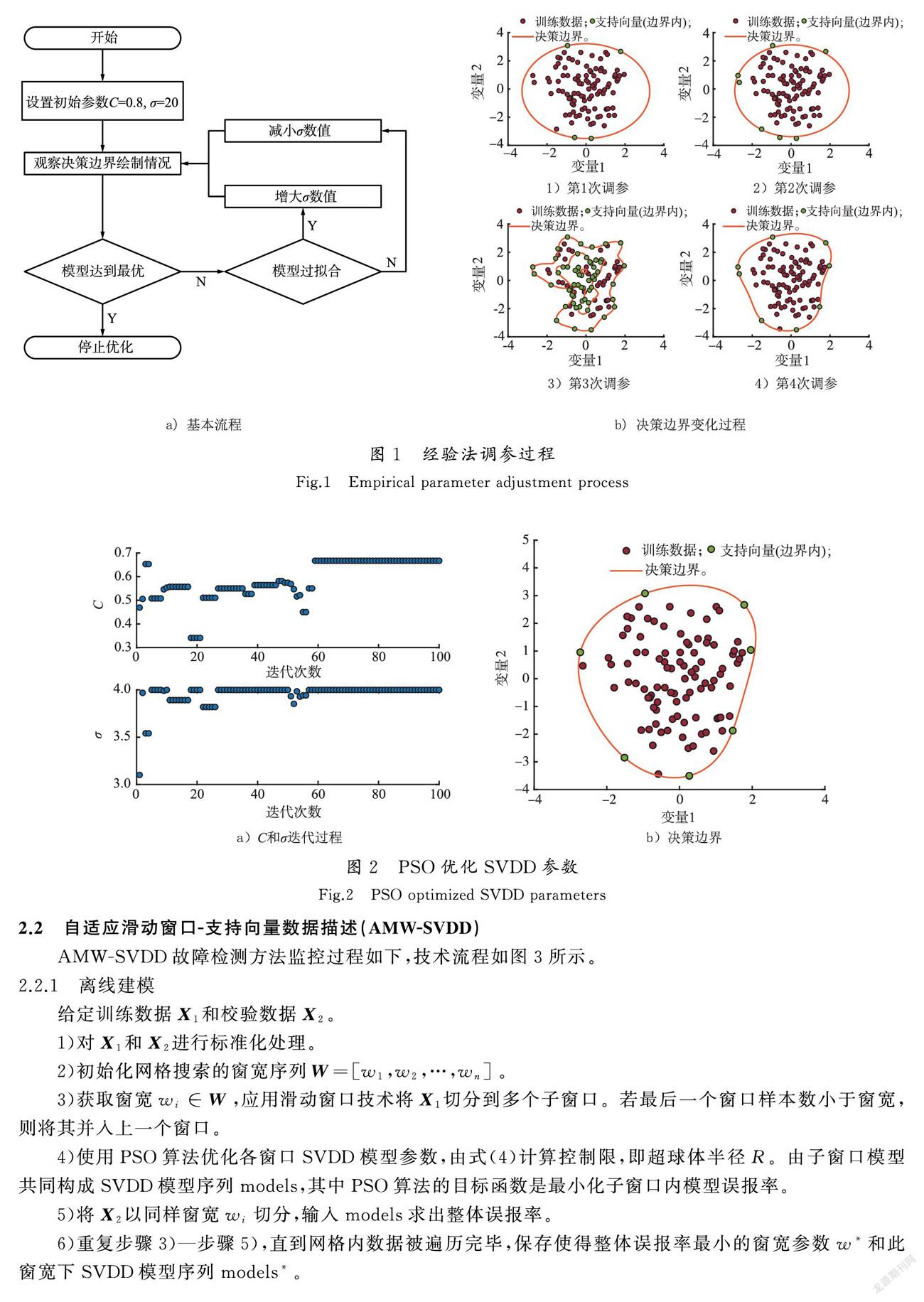
本文通过一个数值例子验证PSO方法的有效性。在二维空间中随机生成100个均值为[0 0]、协方差矩阵为[1 0;0 1]的高斯随机数，分别使用经验值法和PSO方法对SVDD模型调参。其中经验值法调参流程如图1 a）所示，调参过程模型变化情况如图1 b）所示;PSO算法迭代过程中C和σ变化如图2 a）所示，最终决策边界绘制如图2 b）所示。

通过对比图1 b）和图2 b），可以发现使用经验值法和PSO法所得模型决策边界基本一致。由此可以得出，相较于经验调参法，PSO方法在不降低模型性能的前提下大大减少了模型调参的时间成本。

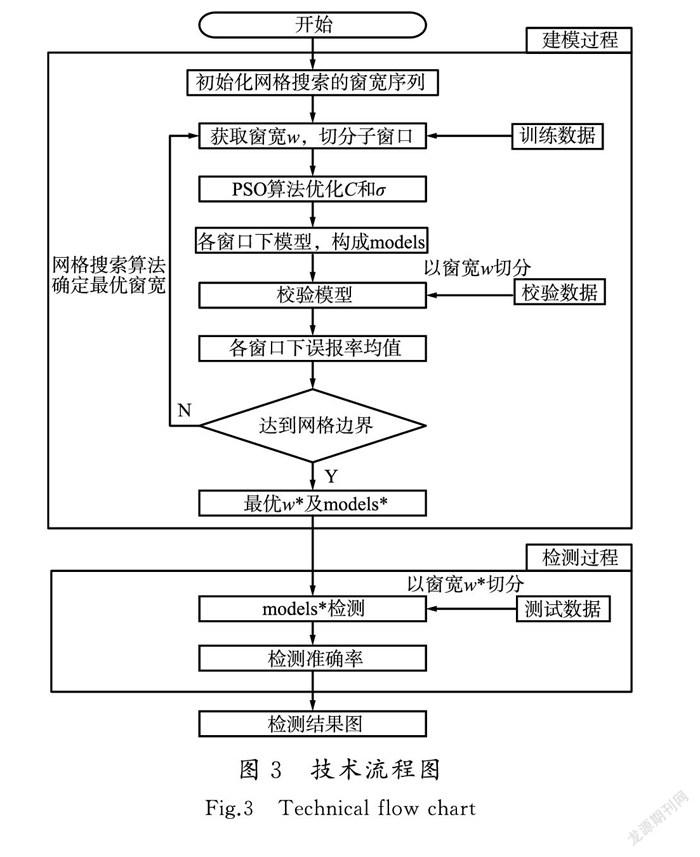
2.2 自适应滑动窗口-支持向量数据描述（AMW-SVDD）AMW-SVDD故障检测方法监控过程如下，技术流程如图3所示。

2.2.1 离线建模

给定训练数据X1和校验数据X2。

1）对X1和X2进行标准化处理。

2）初始化网格搜索的窗宽序列W=[w1，w2，…，wn]。

3）获取窗宽wi∈W，应用滑动窗口技术将X1切分到多个子窗口。若最后一个窗口样本数小于窗宽，则将其并入上一个窗口。

4）使用PSO算法优化各窗口SVDD模型参数，由式（4）计算控制限，即超球体半径R。由子窗口模型共同构成SVDD模型序列models，其中PSO算法的目标函数是最小化子窗口内模型误报率。

5）将X2以同样窗宽wi切分，输入models求出整体误报率。

6）重复步骤3）—步骤5），直到网格内数据被遍历完毕，保存使得整体误报率最小的窗宽参数w*和此窗宽下SVDD模型序列models*。

2.2.2 在线监测

1）对于测试数据X*，利用训练数据的均值和标准差进行标准化。

2）将X*按w*进行划分，输入models*，由式（6）计算得到D。

3）比较D与R的大小，若D

则，为故障样本。

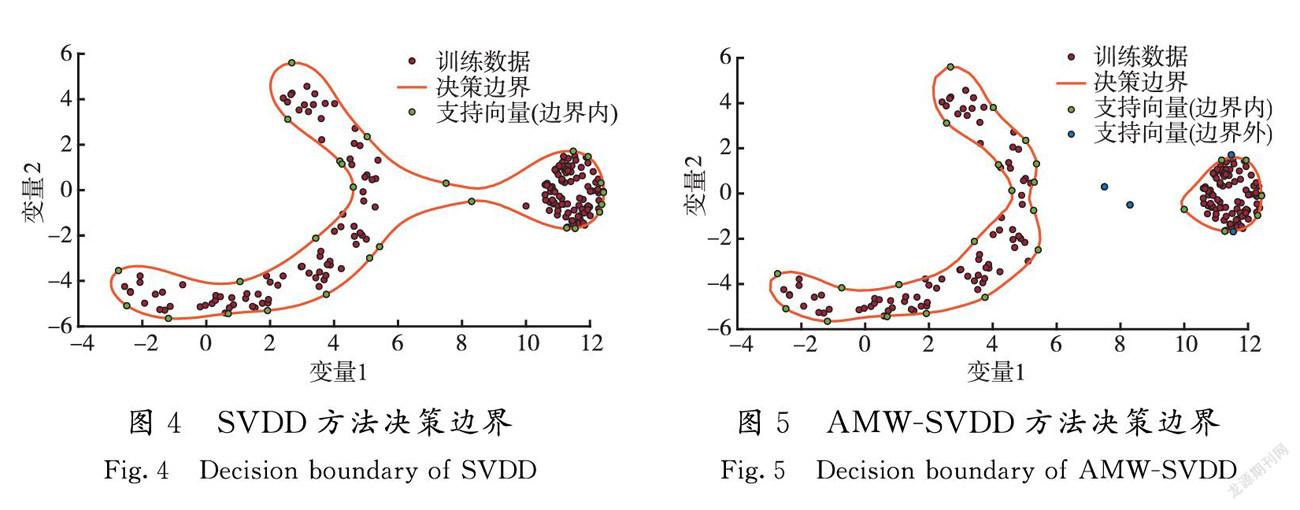
本文引用文献[26]中的一个二维数值例子以证明所提方法的优点。生成100个密度较低的香蕉形正常样本和100个密度较高的圆形正常样本，然后将3个离散点添加到训练样本中。图4为用SVDD方法建模所得决策边界，根据文献[26]，此时模型达到最优。图5为AMW-SVDD方法建模所得决策边界，建模阶段最优窗宽为100。

通过对比图4和图5可以发现，若故障数据出现在离散点附近，AMW-SVDD方法可以有效检测。使用SVDD方法建模时，超球体会将2种模态数据及离散点全部包围，当故障数据出现在离散点附近时，SVDD方法无法有效检测;而本文方法将数据划分到2个子窗口，各窗口模型由PSO方法分别调优。其中，包含离散点的窗口建模时通过调参可以将距离数据中心较远的样本识别为外部支持向量，排除在决策边界外。由于各子窗口决策边界均只包含了密集模态数据，故本文方法可以检测出模态间冗余区域内的故障点。

3 仿真实验

本文以文献[27]中的一个多模态数值例子证明本文方法的有效性。模拟数据包含5个变量，由式（7）生成。

x1=0.576 8s1+0.376 6s2+e1，x2=0.738 2s21+0.056 6s2+e2，x3=0.829 1s1+0.400 9s22+e3，x4=0.651 9s1s2+0.207 0s2+e4，x5=0.397 2s1+0.804 5s2+e5，（7）

其中e1～e5是均值为0、标准差为0.01的噪声序列。

model 1：s1～U（-10，-7）; s2～N（-15，1），model 2：s1～U（2，5）; s2～N（7，1）。（8）

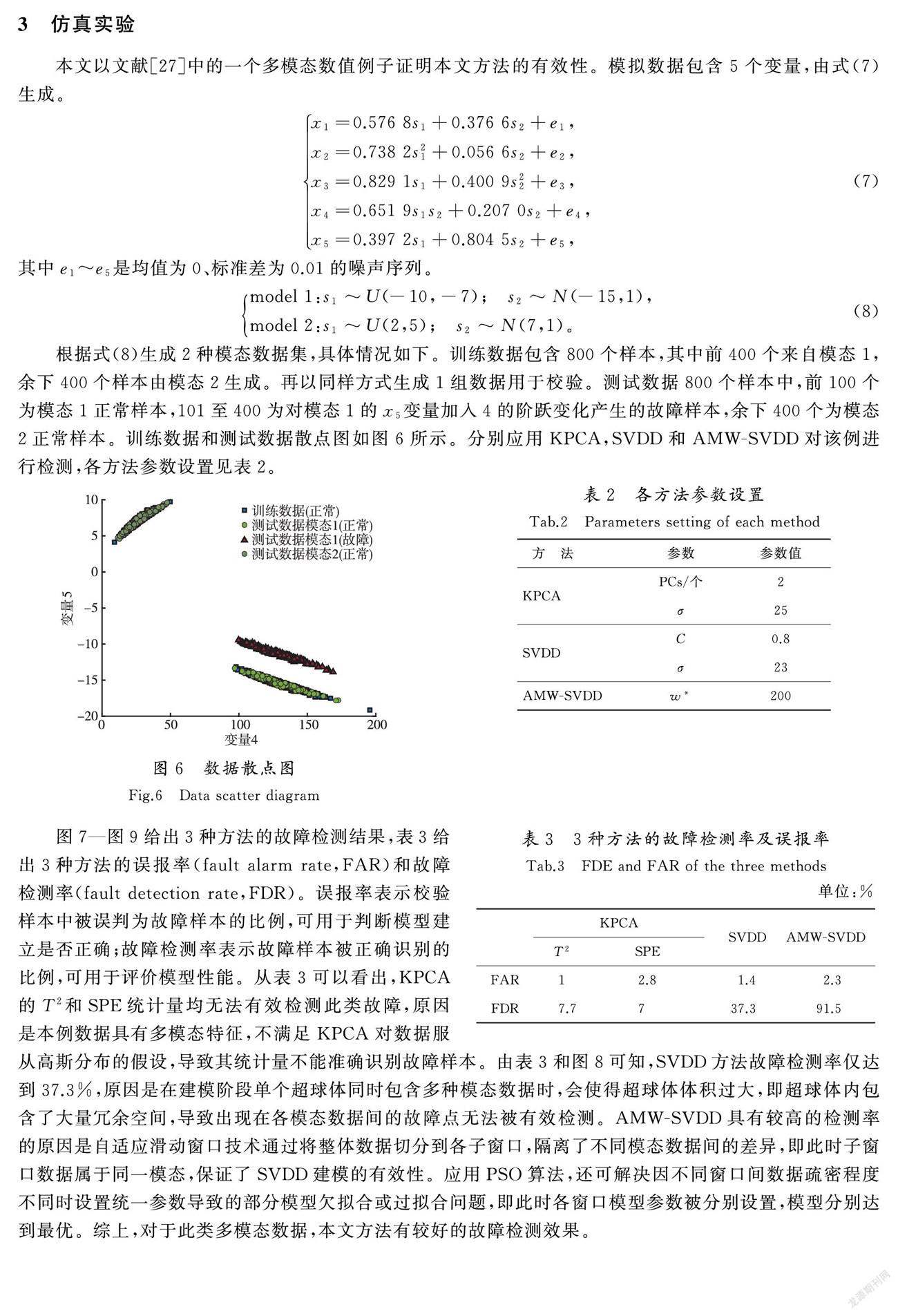
根据式（8）生成2种模态数据集，具体情况如下。训练数据包含800个样本，其中前400个来自模态1，余下400个样本由模态2生成。再以同样方式生成1组数据用于校验。测试数据800个样本中，前100个为模态1正常样本，101至400为对模态1的x5变量加入4的阶跃变化产生的故障样本，余下400个为模态2正常样本。训练数据和测试数据散点图如图6所示。分别应用KPCA，SVDD和AMW-SVDD对该例进行检测，各方法参数设置见表2。

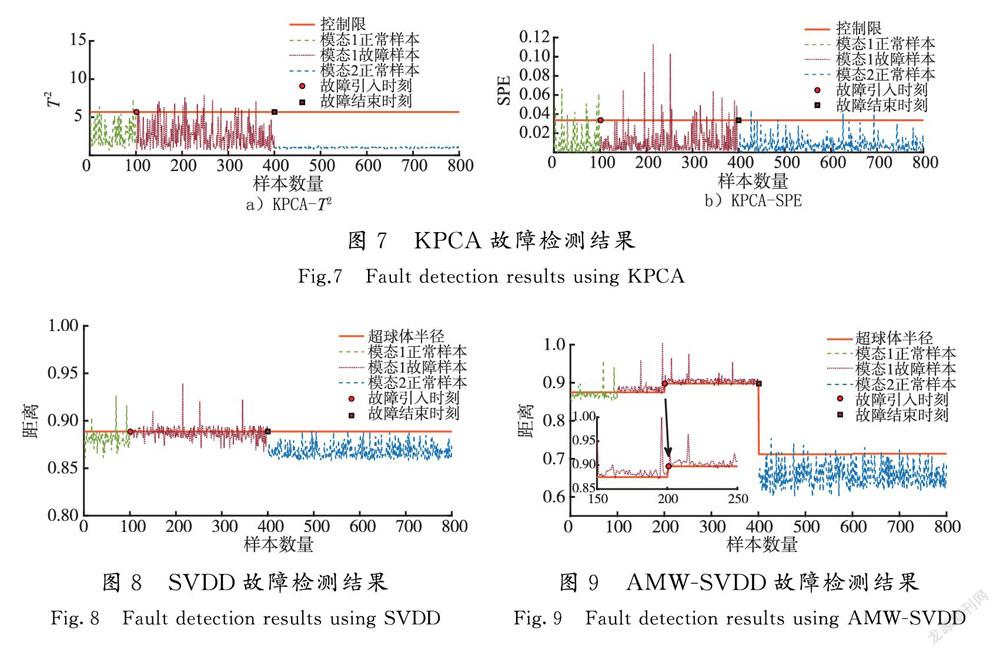
表3给出3种方法的误报率（fault alarm rate，FAR）和故障检测率（fault detection rate，FDR）。误报率表示校验样本中被误判为故障样本的比例，可用于判断模型建立是否正确;故障检测率表示故障样本被正确识别的比例，可用于评价模型性能。从表3可以看出，KPCA的T2和SPE统计量均无法有效检测此类故障，原因是本例数据具有多模态特征，不满足KPCA对数据服从高斯分布的假设，导致其统计量不能准确识别故障样本。由表3和图8可知，SVDD方法故障检测率仅达到37.3%，原因是在建模阶段单个超球体同时包含多种模态数据时，会使得超球体体积过大，即超球体内包含了大量冗余空间，导致出现在各模态数据间的故障点无法被有效检测。AMW-SVDD具有较高的检测率的原因是自适应滑动窗口技术通过将整体数据切分到各子窗口，隔离了不同模态数据间的差异，即此时子窗口数据属于同一模态，保证了SVDD建模的有效性。应用PSO算法，还可解决因不同窗口间数据疏密程度不同时设置统一参数导致的部分模型欠拟合或过拟合问题，即此时各窗口模型参数被分别设置，模型分别达到最优。综上，对于此类多模态数据，本文方法有较好的故障检测效果。

4 TE过程

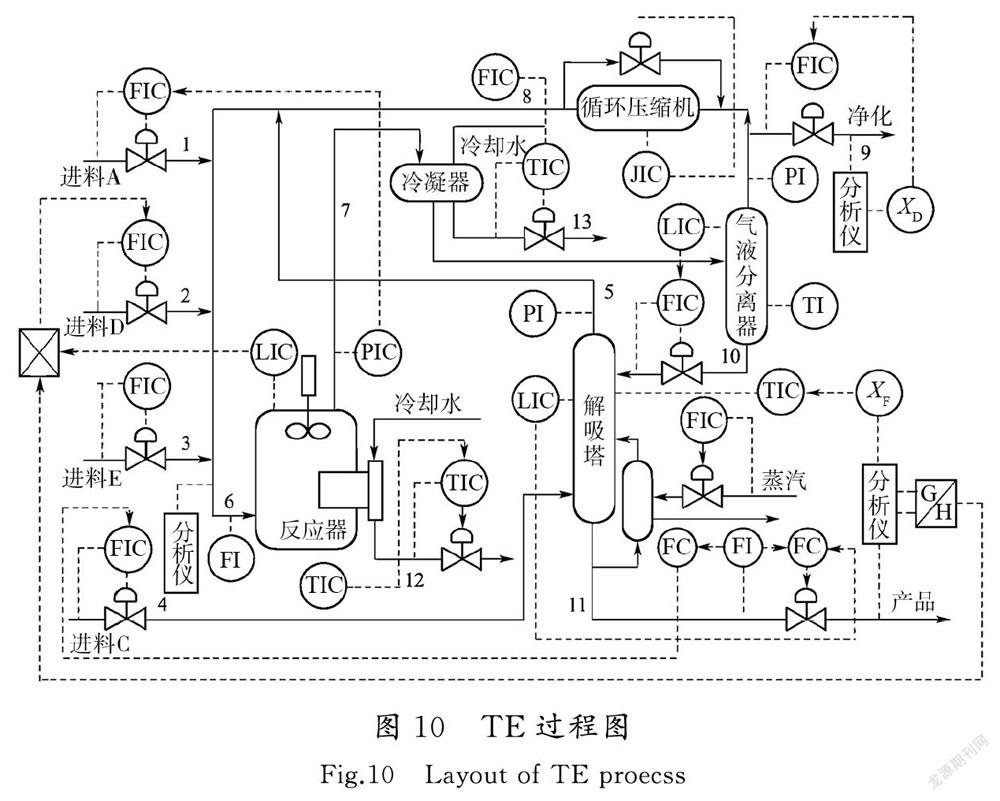
TE过程作为一个完备的工业过程数据仿真平台，已经被广泛应用于故障诊断的研究中[28]，其基本结构如图10所示。TE过程共包含41个测量变量和12个控制变量，本文选用其中50个变量进行实验。TE仿真器可以模拟6种工作环境，每种工作环境可以生成28种故障情况[29]，本文选用模态1和模态3两种工况数据进行监控。

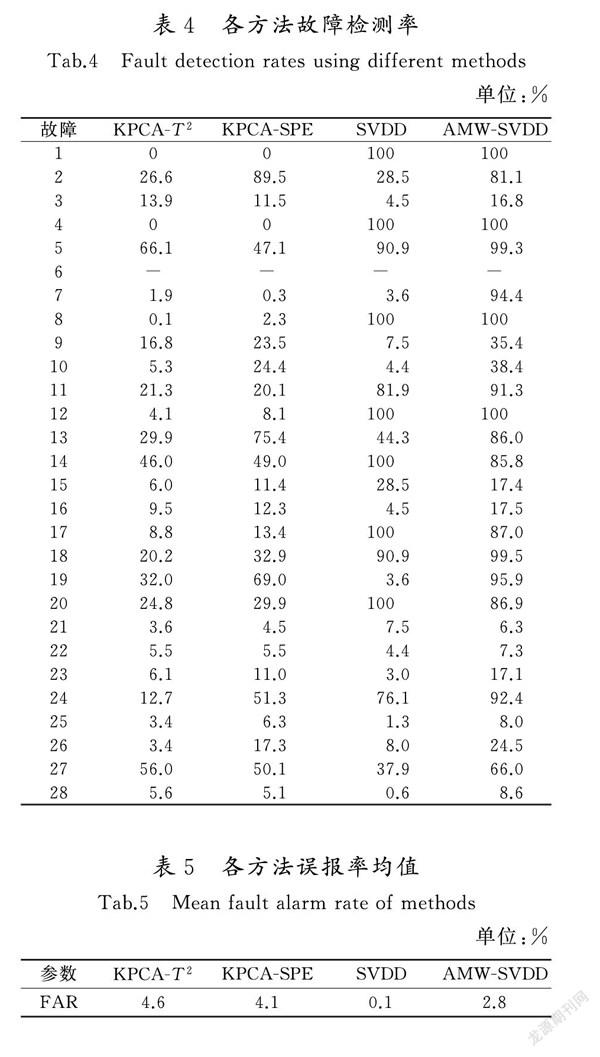
训练数据包含2 000个样本点，其中前1 000个在模态1正常工况下采集，余下样本点在模态3正常工况下采集，以同样方式再生成1组数据用于校验。测试数据与训练数据样本数相同，前1 000个由模态1正常工况生成，余下的1 000个样本来自模态3，各种故障均在模态3的第200时刻引入。利用AMW-SVDD方法进行故障检测，并与KPCA-T2，KPCA-SPE，SVDD进行对比分析。KPCA核主元个数选取为18，核参数σ=25，置信度α=95%，SVDD方法C=0.8，σ=20，AMW-SVDD方法最优窗宽为200。表4和表5分别给出了各方法在不同故障数据集的故障检测率和全部数据集的误报率均值。

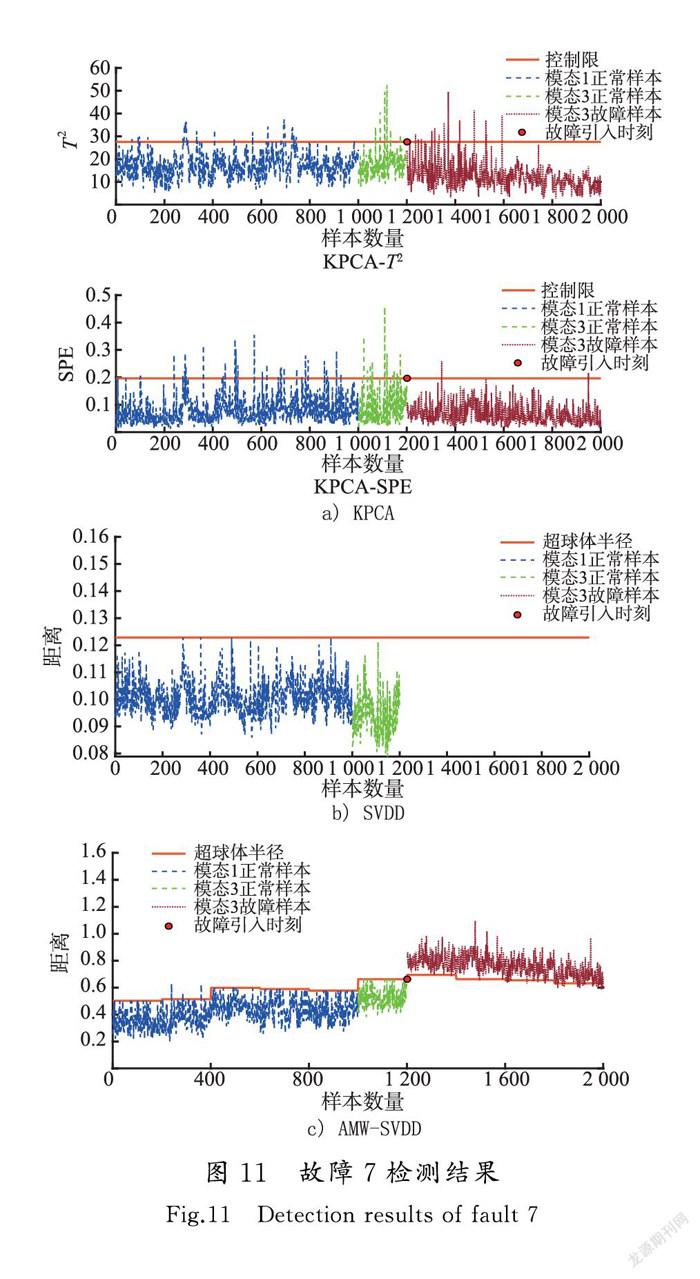
综合对比上述方法在TE数据集上的检测效果，KPCA方法2个统计量检测效果均有限，原因是具有多模态特征的数据，整体并不服从多元高斯分布，这与T2和SPE统计量的适用范围相违背。进一步分析发现T2统计量检测效果远不及SPE统计量，原因是主元子空间通常保留数据正常特征，而残差子空间主要描述噪声，所以T2控制限覆盖范围通常远大于SPE控制限，因此SPE统计量更易检测出相对微小的故障，导致其检测性能优于T2。SVDD方法检测率相对较低，原因是SVDD方法对多模态数据建模时无法正确处理多模态数据的分布特征。当原始数据具有多个模态时，传统SVDD方法仍然试图寻找单一超球体同时包围多个模态数据，使得模态间冗余空间被大量包含在超球体内部，当故障样本出现在冗余空间时，其到超球体球心距离同样小于半径，SVDD方法无法对此类故障进行有效检测。AMW-SVDD方法检测效果最优，主要原因是该方法通过自适应窗口技术切分数据，使得同一窗口数据属于同一模态，并且应用PSO算法对各窗口模型分别调优，成功将模态间的冗余空间排除在超球体外部，进一步隔离了整体数据的多模态特性，因此具有较高的故障检测率。图11给出了各方法对故障7的检测结果，可以直观发现，AMW-SVDD方法所得统计量在故障发生后绝大部分时间内保持超出控制限的状态，而其余方法的统计量在整个故障发生阶段基本都未能超出控制限，说明本文方法检测效果远高于传统故障检测方法。另外，由表5可知，各方法的误报率均控制在5%以下，说明模型都没有出现过拟合现象，保证了实验结果的有效性。需要说明的是，在规定时间内生成故障6数据时会缺失约1/3样本，故将其舍去。由于舍去故障6数据后本节实验仍剩余27组故障数据，实验样本已经足够充分，且表4中其他27种故障的检测结果可以证明本文方法对多模态数据检测性能的优越性，故舍去故障6数据对本节实验结果不会产生较大影响。综上所述，本文方法是一种适用于多模态过程的故障检测方法。

5 结 语

为提高传统SVDD方法在多模态过程中的监控性能，提出了基于AMW-SVDD的多模态过程故障检测方法。该方法通过结合网格搜索方法和滑动窗口技术，实现自适应确定窗宽参数，从而以最优窗宽为标准将整体多模态数据切分为多个子单模态数据，可有效隔离数据的多模态特性。在子窗口内数据属于同一模态的基础上，引入粒子群优化算法，为各子窗口SVDD模型分别优化参数，解决不同子窗口内数据疏密程度不同时使用同一参数无法同时调优全部模型的问题。AMW-SVDD方法通过将数据特征由全局分解到局部，可成功处理数据的多模态特性。在数值例子及TE数据集上的实验结果表明，相比传统故障检测方法，在处理多模态过程时，AMW-SVDD方法具有更高的过程监控性能。

本文主要针对多模态数据进行研究，但是实际工业过程中数据间往往还具有很强的自相关性，接下来将考虑如何解决过程中的动态性问题，提高算法在不同场景的适应性。

参考文献/References：

[1] 刘强，卓洁，郎自强，等.数据驱动的工业过程运行监控与自优化研究展望[J].自动化学报，2018，44（11）：1944-1956.

LIU Qiang，ZHUO Jie，LANG Ziqiang，et al.Perspectives on data-driven operation monitoring and self-optimization of industrial processes[J].Acta Automatica Sinica，2018，44（11）：1944-1956.

[2] HAMADACHE M，LEE D.Principal component analysis based signal-to-noise ratio improvement for inchoate faulty signals：Application to ball bearing fault detection[J].International Journal of Control Automation and Systems，2017，15（2）：506-517.

[3] BIN SHAMS M A，BUDMAN H M，DUEVER T A.Fault detection，identification and diagnosis using CUSUM based PCA[J].Chemical Engineering Science，2011，66（20）：4488-4498.

[4] 胡益，王麗，马贺贺，等.基于核PLS方法的非线性过程在线监控[J].化工学报，2011，62（9）：2555-2561.

HU Yi，WANG Li，MA Hehe，et al.Online nonlinear process monitoring using kernel partial least squares[J].CIESC Journal，2011，62（9）：2555-2561.

[5] WANG L，SHI H B.Improved kernel PLS-based fault detection approach for nonlinear chemical processes[J].Chinese Journal of Chemical Engineering，2014，22（6）：657-663.

[6] 彭开香，马亮，张凯.复杂工业过程质量相关的故障检测与诊断技术综述[J].自动化学报，2017，43（3）：349-365.

PENG Kaixiang，MA Liang，ZHANG Kai.Review of quality-related fault detection and diagnosis techniques for complex industrial processes[J].Acta Automatica Sinica，2017，43（3）：349-365.

[7] 李晗，萧德云.基于数据驱动的故障诊断方法综述[J].控制与决策，2011，26（1）：1-9.

LI Han，XIAO Deyun.Survey on data driven fault diagnosis methods[J].Control and Decision，2011，26（1）：1-9.

[8] MCAVOY T J，YE N.Base control for the Tennessee Eastman problem[J].Computers & Chemical Engineering，1994，18（5）：383-413.

[9] RUSSO L P，BEQUETTE B W.Effect of process design on the open-loop behavior of a jacketed exothermic CSTR[J].Computers & Chemical Engineering，1996，20（4）：417-426.

[10]SCHLKOPF B，SMOLA A，MLLER K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation，1998，10（5）：1299-1319.

[11]贾润达，毛志忠，王福利.基于KPLS模型的间歇过程产品质量控制[J].化工学报，2013，64（4）：1332-1339.

JIA Runda，MAO Zhizhong，WANG Fuli.KPLS model based product quality control for batch processes[J].CIESC Journal，2013，64（4）：1332-1339.

[12]LEE J M，YOO C K，CHOI S W，et al.Nonlinear process monitoring using kernel principal component analysis[J].Chemical Engineering Science，2004，59（1）：223-234.

[13]赵孝礼，赵荣珍.全局与局部判别信息融合的转子故障数据集降维方法研究[J].自动化学报，2017，43（4）：560-567.

ZHAO Xiaoli，ZHAO Rongzhen.A method of dimension reduction of rotor faults data set based on fusion of global and local discriminant information[J].Acta Automatica Sinica，2017，43（4）：560-567.

[14]ZHANG Y W，MA C.Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS[J].Chemical Engineering Science，2011，66（1）：64-72.

[15]张成，郭青秀，李元，等.基于主元分析得分重构差分的故障检测策略[J].控制理论与应用，2019，36（5）：774-782.

ZHANG Cheng，GUO Qingxiu，LI Yuan，et al.Fault detection strategy based on difference of score reconstruction associated with principal component analysis[J].Control Theory & Applications，2019，36（5）：774-782.

[16]TAX D M J，DUIN R P W.Support vector domain description[J].Pattern Recognition Letters，1999，20（11/12/13）：1191-1199.

[17]劉家辰，苗启广，宋建锋，等.使用聚类稳定性分析方法增强单类学习算法[J].西安电子科技大学学报，2015，42（2）：58-64.

LIU Jiachen，MIAO Qiguang，SONG Jianfeng，et al.Enhanced one-class learning based on clustering stability analysis[J].Journal of Xidian University，2015，42（2）：58-64.

[18]刘伟旻，王建林，邱科鹏，等.基于DHSC的多模态间歇过程测量数据异常检测方法[J].化工学报，2017，68（11）：4201-4207.

LIU Weimin，WANG Jianlin，QIU Kepeng，et al.Method for detecting abnormal data in multimode batch processes based on dynamic hypersphere structure change[J].CIESC Journal，2017，68（11）：4201-4207.

[19]ZHAO S J，ZHANG J，XU Y M.Performance monitoring of processes with multiple operating modes through multiple PLS models[J].Journal of Process Control，2006，16（7）：763-772.

[20]HE Q P，WANG J.Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes[J].IEEE Transactions on Semiconductor Manufacturing，2007，20（4）：345-354.

[21]ZHAO S J，ZHANG J，XU Y M.Monitoring of processes with multiple operating modes through multiple principle component analysis models[J].Industrial & Engineering Chemistry Research，2004，43（22）：7025-7035.

[22]CHU Y H，QIN S J，HAN C H.Fault detection and operation mode identification based on pattern classification with variable selection[J].Industrial & Engineering Chemistry Research，2004，43（7）：1701-1710.

[23]馬贺贺，胡益，侍洪波.基于马氏距离局部离群因子方法的复杂化工过程故障检测[J].化工学报，2013，64（5）：1674-1682.

MA Hehe，HU Yi，SHI Hongbo.Fault detection of complex chemical processes using Mahalanobis distance-based local outlier factor[J].CIESC Journal，2013，64（5）：1674-1682.

[24]杨雅伟，宋冰，侍洪波.多SVDD模型的多模态过程监控方法[J].化工学报，2015，66（11）：4526-4533.

YANG Yawei，SONG Bing，SHI Hongbo.Multimode processes monitoring methodvia multiple SVDD model[J].CIESC Journal，2015，66（11）：4526-4533.

[25]LI H，WANG H G，FAN W H.Multimode process fault detection based on local density ratio-weighted support vector data description[J].Industrial & Engineering Chemistry Research，2017，56（9）：2475-2491.

[26]KENNEDY J，EBERHART R.Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks.Perth：IEEE，1995：1942-1948.

[27]MA H H，HU Y，SHI H B.Fault detection and identification based on the neighborhood standardized local outlier factor method[J].Industrial & Engineering Chemistry Research，2013，52（6）：2389-2402.

[28]RATO T J，REIS M S.Fault detection in the Tennessee Eastman benchmark process using dynamic principal components analysis based on decorrelated residuals （DPCA-DR）[J].Chemometrics and Intelligent Laboratory Systems，2013，125：101-108.

[29]BATHELT A，LAWRENCE RICKER N，JELALI M.Revision of the Tennessee Eastman process model[C]//9th International Symposium on Advanced Control of Chemical Processes.Whistler：[s.l.]，2015：309-314.

3189501908242