基于空间矢量相位偏移的三相变流器容错优化控制

孙 超，邱颖宁，冯延晖，秦 伟

（南京理工大学能源与动力工程学院，江苏省南京市 210094）

0 引言

随着风力发电技术的普及，风电在电力系统中的占比不断提高［1-2］。在直驱式永磁同步风力发电系统中，用于电机控制与电能传输的三相AC/DC变流器是必不可少的。与永磁同步发电机相比，电力电子开关设备通常工作于高电压、高功率等电气环境之中，因而更容易发生故障［3］。而且相比于不可控功率开关，全控型功率开关器件的门极需要接受高频控制信号，所以在系统中，可控型功率开关管是最容易发生故障的设备。为了提高风力发电系统的安全性、可靠性、经济性，除了优化变流器的控制策略参数［4-6］，对三相变流器容错运行以及优化控制的研究也十分必要。

根据三相AC/DC 变流器的运行结构拓扑，可将其分为2 类：一种是多级并联运行方式，另一种是单级运行方式［7］。当单个功率开关器件发生开路故障时，多级并联的运行方式能够通过控制算法和开关切换，实现对开路故障的全比例补偿容错，但开路故障前的控制算法无法继续使用，且多级并联三相AC/DC 变流器由于拓扑较为复杂、成本较高，因而使用范围没有单级运行的三相AC/DC 变流器广泛。

根据容错电路拓扑结构的不同，可以将单级三相AC/DC 变流器的开路故障容错控制方法分为3类：冗余系统结构、三相四桥臂结构和三相三桥臂结构。冗余系统结构需要将另一组三相变流器与主电路中的三相变流器进行并联，两者之间通过可控型晶闸管进行切换，实现容错控制［8-9］。三相四桥臂结构容错方式相比于冗余系统结构，只需要增加一个冗余桥臂，当主电路中某一相单管或同一相的双管发生开路故障时，利用冗余桥臂替换故障桥臂进行工作［10-12］。

三相三桥臂容错控制方式不需要增加冗余开关设备，降低了系统的硬件成本，且容错控制方式更加灵活。文献［13-14］利用未发生开路故障的功率开关重新构建电压空间矢量，对参考电压矢量进行合成。但该容错方法只能处理同一相功率开关发生开路故障的情况，无法实现不同相功率开关开路故障的容错控制。文献［15-16］利用正常零矢量替换故障零矢量实现容错控制，但没有考虑到开路故障后的有效矢量畸变，故无法实现全比例补偿容错。文献［17-18］考虑了有效矢量的畸变问题，在设计容错控制方法时，剔除了故障有效矢量，仅利用未受开路故障影响的有效矢量和零矢量完成容错控制，但单一有效矢量和零矢量同样无法实现对参考矢量的全比例合成。文献［19］通过设计零d轴电流控制算法，实现容错控制，但仍然没有考虑开路故障对有效矢量的影响。文献［20-21］基于模型预测控制（model predictive control，MPC）提出了容错控制方法，该方法根据电机模型，预测得到下一个时刻的系统运行状态，进行最优矢量的选择，相比于空间矢量脉宽调制（space vector pulse width modulation，SVPWM）控制算法，该算法只能选择与参考电压空间矢量近似的基础矢量来实现容错控制，同样无法进行全比例合成，且基于MPC 的容错控制算法比SVPWM 控制算法计算量更大。

SVPWM 算法利用基础电压空间矢量来合成参考电压空间矢量，具有算法简单、控制效果好等优点，因而成为应用最广泛的调制策略之一［22］，通常用于控制两电平功率变流器。但是，由于目前的三相三桥臂结构容错控制方式无法实现全比例补偿，导致三相电流仍然存在畸变，使得参考电压空间矢量和电流矢量之间存在不可忽视的相位差。而通过对上述容错控制方法的分析不难发现，已有的容错控制方法都是以参考电压空间矢量和电流矢量同相位为前提进行设计的，从而导致容错效果不佳。本文以三相AC/DC 变流器为研究对象，通过建立参考电压空间矢量和电流矢量相位差的数学模型，分析得到开路故障前后参考电压空间矢量和电流矢量之间相位差的变化，提出了基于空间矢量相位偏移的容错优化控制方法，并以八扇区矢量投影容错控制方式为基础进行容错控制，并通过仿真和实验验证所提出的容错优化控制方法的可行性与有效性。

1 基于相位偏移的容错优化控制方法

1.1 开路故障分析

三相AC/DC 变流器结构拓扑如附录A 图A1所示。各相功率开关状态由开关变量Sa、Sb、Sc决定：当开关变量为1 时，表示该相上管导通，下管关断；当开关变量为0 时，则表示该相上管关断，下管导通。由开关变量状态可定义SVPWM 中8 个基础矢量：V0、V1、V2、V3、V4、V5、V6、V7。三相AC/DC变流器功率开关发生开路故障后，系统运行情况受三相电流流向的影响，以a 相功率开关发生开路故障前后为例，a 相电流ia流向、a 相桥臂功率开关状态与系统运行状态之间的关系如附录A 图A2（a）、（b）所示。从图A2（a）可以看出，当ia＞0 且开关变量Sa=1 时，电流经过反并联续流二极管D1 流向负载，此时系统运行状态与功率开关S1 是否发生开路故障无关；当开关变量Sa=1 且ia＜0 时，电流本应由S1 流入，但由于S1 开路，电流只能由D4 流入，如图A2（b）所示，系统运行受到开路故障影响，此时开关变量等效为Sa=0，参考电压空间矢量的合成发生变化。S4 及其他功率开关开路故障时系统运行状态同理可以分析得到。

由上述分析可知，开路故障使得原本应该导通的开关无法导通，基础电压空间矢量随之改变，从而导致了参考电压空间矢量的畸变。同时，由于参考电压空间矢量的畸变，其与电流矢量之间的相位差也会增大。

1.2 相位偏移模型

由附录A 图A1，结合永磁同步电机数学模型，可以得到三相电压表达式如下。

式中：us，a、us，b、us，c为三相变流器相电压；ia、ib、ic为三相变流器相电流；Ls为定子电感；np为电机极对数；ωm为电机机械角速度；ψm为永磁体磁链幅值；φm为电机机械角度；φom为电机初始机械角度；Ra、Rb、Rc为三相定子电阻。

由式（1）可以得到：

式中：Rs为等效电阻，且有Rs=Ra=Rb=Rc。

对式（3）进行Park 变换，可得到：

式中：idq为d轴电流id和q轴电流iq构成的矢量；us，dq为d轴电压us，d和q轴电压us，q构成的矢量；ωe为电机电角速度。

由于定子等效电阻较小，且当系统运行稳定后，铜损很小，故可以忽略电阻的大小以及dq轴电流的变化率。根据系统有功功率和无功功率之间的关系计算得到参考电压空间矢量和电流矢量之间的相位差δ0。

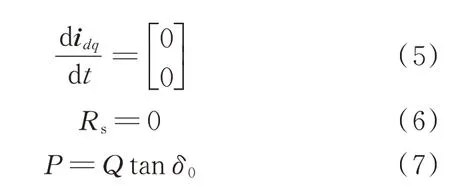
式中：P为系统有功功率；Q为系统无功功率；δ0为电压空间矢量和电流矢量之间的相位差。

将式（5）和式（6）代入式（4）可以得到：

由式（12）可知，电流矢量和电压矢量之间的相位差由定子电感、永磁体磁链以及控制参数id、iq决定。而在机侧控制算法中，当功率开关发生开路故障后，d轴电流分量会偏离于系统设定值，q轴电流分量会围绕系统设定值上下波动。定义开路故障后d轴电流分量为i+d，偏离值为τ，则有：

若要满足已有容错控制方法的设计前提，则需要令开路故障后的电压矢量和电流矢量相位差为零，即令式（12）为零，联立式（12）和式（13）可得：

由式（15）可以解得令参考电压空间矢量和电流矢量相位差为零的d轴电流i+d，利用i+d替换id，即可减小两者之间的相位差，实现容错优化控制。虽然式（15）中2 个解都能满足式（14），但考虑到尽量减小d轴电流变化对系统运行的影响，故需舍去两解中绝对值较大的解（解2），该结论在仿真以及实验结果中会进一步对比说明。

1.3 容错优化控制实现方法

基于空间矢量相位偏移的容错优化控制方法框图如图1 所示。图中：Cf为直流母线电容；Udc为直流母线电压；RL为直流侧负载；θ为电机电角度。

图1 系统控制方法框图Fig.1 Block diagram of system control method

容错控制模块的切换过程具体如下。系统控制算法中设置有SVPWM 模块标志位“0”，以及容错控制模块标志位“1”。当故障诊断模块未检测到功率开关开路故障时，则标志位置“0”，由SVPWM 模块输出6 路PWM 控制信号。而当故障诊断模块检测到功率开关开路故障时，一方面将诊断结果发送给容错控制模块，使其根据不同开关开路故障选择对应的容错控制方式；另一方面，将标志位置“1”，由容错控制模块输出6 路脉宽调制（PWM）控制信号，完成容错控制。

本文在容错控制模块中选择八扇区矢量投影法作为容错模式，八扇区划分方式［17］如附录A 图A3所示。功率开关发生开路故障后，通过八扇区划分方式能够将故障扇区和非故障扇区进行区分。根据受开路故障影响的类型，参考电压空间矢量合成方式可分为如下2 类。

1）只有零矢量受开路故障影响

用正常零矢量替代故障零矢量。以S1 开路故障且参考电压空间矢量位于扇区Ⅲ为例。此时受开路故障影响的矢量仅为零矢量V7，由1.1 节开路故障分析可知，当开关变量Sa=1 且ia＜0 时，开关变量等效为Sa=0，即V7畸变成V4。此时利用零矢量V0替换零矢量V7即可完成容错控制。该扇区内开路故障前后参考电压空间矢量表达式如式（16）和式（17）所示，容错后的参考电压空间矢量Vc如式（18）所示。

式中：ε、η、γ为矢量作用比例；Vr为开路故障前参考电压空间矢量；VS1为S1 开路故障后参考电压空间矢量；Vc为容错后参考电压空间矢量。

2）零矢量和有效矢量受开路故障影响

故障零矢量用正常零矢量进行替换，故障有效矢量用矢量投影法实现对参考电压空间矢量的合成。以S1 开路故障且参考电压空间矢量位于扇区Ⅶ为例。此时，受开路故障影响的矢量为零矢量V7和有效矢量V2，由1.1 节开路故障分析可知，当开关变量Sa=1 且ia＜0 时，开关变量等效为Sa=0，即V7畸变成V4，V2畸变成V3。该扇区内开路故障前后参考电压空间矢量表达式如式（19）和式（20）所示，容错后Vc的表达式如式（21）所示，矢量投影补偿如图2 所示。

图2 矢量投影补偿Fig.2 Vector projection compensation

其余各扇区以及各功率开关开路故障时，同理进行容错控制。

2 仿真及实验验证

2.1 仿真验证

仿真系统参数如附录A 表A1 所示。若参考电压空间矢量和电流矢量同相位，则当a 相电流ia由正到负过零点时，参考电压空间矢量正好位于六扇区划分方式下扇区Ⅱ的中点处，此时参考电压空间矢量和电流矢量与β轴正方向重合。为了方便比较参考电压空间矢量和电流矢量之间的相位关系，选取β轴正方向为观测轴，当a 相电流ia由正到负过零点时，电流矢量与β轴正方向重合。此时，参考电压空间矢量和β轴正方向间的角度，即为参考电压空间矢量和电流矢量之间的相位差。六扇区划分方式如附录A 图A4 所示，当系统无开路故障发生时，仿真结果如附录A 图A5 所示，图中虚线为a 相电流由正到负过零点时对应的扇区位置。不难看出，当ia由正到负过零点时，参考电压空间矢量所处扇区位置为六扇区划分方式下的扇区Ⅱ的中点处（β轴正方向），此时电流矢量和电压矢量相位差接近于零。

当S1 发生开路故障后，仿真结果如附录A 图A6 所示。从图中可以看出，S1 开路后，当ia由正到负过零点时（电流矢量位于β轴正方向时），电压空间矢量所处扇区为扇区Ⅲ，参考电压空间矢量和电流矢量之间出现了较大的相位差。

选择基于矢量投影的八扇区容错控制方法进行容错控制，容错后的仿真结果如附录A 图A7 所示。从图中可以看出，利用八扇区容错控制方法后，当ia由正到负过零点时（电流矢量位于β轴正方向），此时电压空间矢量所处扇区为八扇区划分方式下扇区Ⅲ（八扇区划分方式如附录A 图A3 所示），参考电压空间矢量和电流矢量之间仍然存在较大的相位差。

加入容错优化控制算法后的仿真结果如附录A图A8 所示。从图A8（a）结果可以看出，利用容错优化控制方法后，ia由正到负过零点时，对应的参考电压空间矢量所处扇区位置为扇区Ⅱ，参考电压空间矢量和电流矢量之间的相位差减小，容错优化后三相电流波形更加接近于无开路故障时电流波形；同时，采用式（15）中的解2 进行容错优化后，虽然对应的参考电压空间矢量也处于扇区Ⅱ，但相比于图A8（a）中的结果，参考电压空间矢量和电流矢量之间相位差较大，且容错后三相电流峰值附近的波形出现明显的畸变，容错效果较图A8（a）差。

为了方便比较各情况下两者相位关系，图3 和表1 给出了无开路故障、S1 开路故障、容错以及容错优化情况下，参考电压空间矢量相对于电流矢量（β轴正方向）的位置。其中，iref为电流矢量；Vref，nor为无开路故障时参考电压空间矢量；Vref，S1为开路故障后参考电压空间矢量；Vref，S1，comp为容错后参考电压空间矢量；Vref，S1，opt为容错优化后参考电压空间矢量；Vref，S1，dopt为采用式（15）中解2 进行容错优化后的参考电压空间矢量。表1 中规定逆时针方向为相位的正方向。

图3 仿真矢量相对位置Fig.3 Relative position of simulated vectors

表1 仿真矢量相位Table 1 Phase of simulated vectors

从图3 以及表1 中可以看出，开关管发生开路故障后，参考电压空间矢量处于扇区Ⅲ，与电流矢量之间的相位差为68.38°；使用容错控制算法后，虽然两者之间的相位差减小至54.74°，但参考电压空间矢量仍然处于扇区Ⅲ；使用容错优化算法后，参考电压空间矢量恢复到扇区Ⅱ，两者之间相位差为−6.83°；采用式（15）中的解2 进行容错优化后，虽然参考电压空间矢量恢复到扇区Ⅱ，但两者之间相位差为−23.96°。仿真结果表明，所提出的容错优化方法能够有效减小参考电压空间矢量和电流矢量之间的相位差，优化系统输出三相电流波形，提升系统容错运行效果。同时，对比式（15）中2 个解对应的容错效果可知，虽然2 个解都能有效减小参考电压空间矢量和电流矢量之间的相位差，但绝对值较小的解，取得的容错效果更佳，故在实际应用中舍去式（15）中绝对值较大的解。

2.2 实验验证

本文为了验证所提出的容错优化控制方法的可行性及有效性，模拟直驱式永磁同步风力发电系统机侧结构，搭建了验证平台。实验平台结构如附录A 图A9 所示，实验平台实物如附录A 图A10 所示。实验平台主电路部分主要包括电网、变频器、电机对拖平台、三相变流器、直流电容及负载，其中电机对拖平台是为了模拟风轮系统拖动永磁同步发电机转动，实现由机械能向电能转换的过程。实验系统主要参数如附录A 表A2 所示。

对照仿真结果，对正常情况、S1 开路故障、八扇区容错控制、容错优化控制进行实验对比，三相电流和参考电压空间矢量所在扇区的对照实验结果如图4（a）至图4（f）以及表2 所示，图中虚线为a 相电流由正到负过零点时对应的扇区位置。

表2 实验矢量相位Table 2 Phase of experiment vectors

图4 实验结果Fig.4 Experimental results

从图4 及表2 可以看出，实验结果与仿真结果一致：图4（a）为系统无故障实验结果，当ia由正到负过零点时，参考电压空间矢量所处位置接近六扇区划分方式中扇区Ⅱ的中点，此时参考电压空间矢量和电流矢量相位差为3.48°；图4（b）为系统S1 故障实验结果，当ia由正到负过零点时，参考电压空间矢量所处位置为六扇区划分方式中扇区Ⅳ，此时参考电压空间矢量和电流矢量之间出现较大的相位偏移，两者之间相位差为109.86°；图4（c）为系统采用八扇区容错控制后实验结果，当ia由正到负过零点时，参考电压空间矢量所处位置为八扇区划分方式中扇区Ⅳ，此时参考电压空间矢量和电流矢量之间的相位偏移虽然减小至92.98°，但仍然较大，影响了容错效果；图4（d）为系统采用基于相位偏移的容错优化控制算法后实验结果，当ia由正到负过零点时，参考电压空间矢量所处位置为八扇区划分方式中扇区Ⅱ，此时参考电压空间矢量和电流矢量之间的相位差为−3.67°，同时当ia过零点时，三相电流波形显著改善；图4（e）为系统采用式（15）中解2 进行容错优化后实验结果，当ia由正到负过零点时，参考电压空间矢量同样位于八扇区划分方式中扇区Ⅱ，此时参考电压空间矢量和电流矢量之间的相位差为−15.63°，但三相电流波形出现了畸变；图4（f）是各情况下对应于ia由正到负过零点时各矢量的相对位置关系，包括电流矢量iref、正常情况下参考电压空间矢量Vref，nor、S1 开路故障时参考电压空间矢量Vref，S1、容错控制后参考电压空间矢量Vref，S1，comp、容错优化控制后参考电压空间矢量Vref，S1，opt以及采用式（15）中解2 进行容错优化后的参考电压空间矢量Vref，S1，dopt。从图中可以看出，在容错优化控制后，参考电压空间矢量和电流矢量之间的相位差显然减小。同时，式（15）中的解2 虽然也能有效减小参考电压空间矢量和电流矢量之间相位差，但容错效果较差，故在实际应用中舍去该解。

由于实验中的电机、电阻、电感等发热使得阻抗值发生变化，所以故障以及未进行容错优化的实验结果相比于仿真结果，参考电压空间矢量和电流矢量之间相位差更大。但仿真结果以及实验结果都证实了所提出的容错优化方法的可行性与有效性。

电流谐波含量表达式如下［23］：

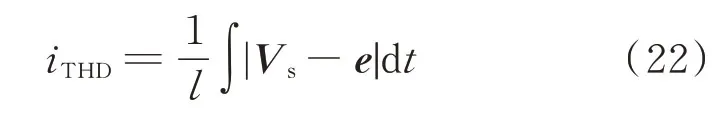
式中：iTHD为定子电流谐波；l为总漏感；Vs为基础电压矢量；e为系统实际输出电压矢量。若参考电压空间矢量与电流矢量相位差增大，则参考电压空间矢量和实际输出电压矢量之间的相位差也会增大，导致了基础电压矢量和实际输出的电压矢量之间偏差增大。根据式（22）可知，当基础电压矢量和实际输出电压矢量的偏差增大，就会导致电流谐波增大。利用容错优化控制方法后，能够有效减小参考电压空间矢量和电流矢量的相位差，所以电流谐波含量也会随之降低。

在各运行情况下的三相电流总谐波畸变率（THD）如表3 所示。不难发现，利用容错优化控制方法得到的三相电流THD 相比于一般的容错控制方法降低了4%～6%，故容错优化控制方法能够有效地提高系统容错效果。同时利用解2 进行容错优化后得到的三相电流THD 较大，故在实际应用中仅选择绝对值较小的解进行优化控制。

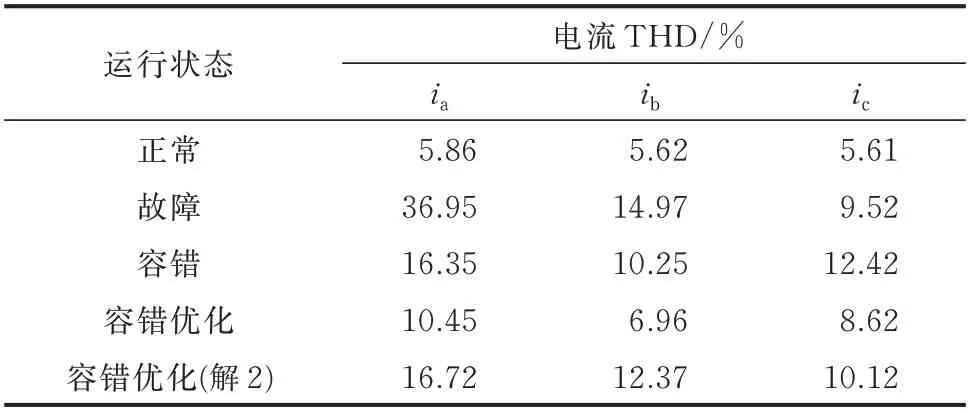
表3 各运行情况下三相电流THDTable 3 Three-phase current THD under various operation conditions

图5 为系统在正常、故障和容错三种情况下动态响应结果。结果表明，系统从发生开路故障到容错只用了0.04 s，该结果表明本文提出的容错优化控制方法能够在系统开路故障后及时对系统进行容错控制，使系统恢复正常运行的能力。

图5 系统动态响应实验结果Fig.5 Experimental results of system dynamic response

3 结语

本文分析了参考电压空间矢量和电流矢量之间相位差在功率开关故障前后的变化，指出了2 个矢量之间的相位偏移导致的容错效果不佳问题，继而提出了基于空间矢量相位偏移的三相AC/DC 变流器容错优化控制方法。仿真及实验结果表明，所提出的容错优化控制方法能够有效减小参考电压空间矢量和电流矢量之间的相位差，改善三相电流输出波形，优化原有容错控制方法。同时，该方法不需要额外的硬件辅助，降低了系统的运行成本，提高了系统在容错状态下的运行效果。

本文未将最大功率跟踪控制算法参数与电机参数进行综合考虑，未来需要进一步加深对该方面的研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。