基于线性判别分析和密度峰值聚类的异常用电模式检测

王建元，张少锋

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林省吉林市 132012）

0 引言

电能的非技术性损失（non-technical loss，NTL）是指用户消费电能后，电力公司却未收到电费的这部分电能［1］。这些损失中，除少部分由电表自身故障产生，大部分是由电力用户的窃电行为导致的［2］。据统计，中国因窃电造成的损失超过总供电损失的6%［3］。除经济上的损失以外，NTL 的存在还会干扰电网运行参数的测算，进而危及电力系统运行的可靠性［4-5］。异常用电检测工作可以找出故障电表和窃电用户，但早期的检测方法仍依赖于现场筛查，耗时耗力。智能电表的普及为电力公司收集了大量细粒度的电力负荷数据［6］，为基于数据驱动的异常用电检测提供了数据来源。

按照是否需要数据标签，可以将电力负荷异常检测算法分为有监督和无监督2 类。有监督算法通过训练集学习异常用户的特征从而获得辨识异常用户的能力，如支持向量机［7-8］、神经网络［9-10］等，其准确度较高，但需要足够量的含标签的样本数据作为支撑。然而，电力负荷数据存在数据类别不平衡的问题，异常用户比例较小，容易使训练过程欠拟合［11］，最终可能降低检测结果的准确度。相比之下，无监督算法的优势是检测过程不需要数据标签，且由于没有训练过程，受数据类别不平衡的影响较小。

目前，基于深度学习的无监督算法多作为有监督检测算法的辅助算法［9，12］，以减少类别不平衡数据对检测结果的负面影响；基于离群因子的无监督算法不适合检测多种用电模式的电力用户负荷［13］。而基于聚类的无监督算法可以实现异常检测全过程（不包括模型评估）的无监督，并且能够实现对多类别电力负荷的异常检测。K均值（K-means）聚类［14］、基于密度的带有噪声的空间聚类（density based spatial clustering of applications with noise，DBSCAN）［15］、近邻传播聚类［16］、离群聚类［17］等在电力负荷异常检测中都有不错的成效。然而，聚类算法用于异常检测存在的问题是参数选取往往基于经验［18］，而无监督算法缺乏异常用户标签，无法评估所选参数的优劣，故难以获取最优参数。

电力负荷异常检测模型通常包含特征构造和异常检测两大模块［19-20］。本文电力负荷异常检测模型流程为：特征构建—维度规约—聚类—异常检测。由于不同类型的电力用户（如城市居民用户、农村居民用户、工商业用户等）往往具有不同类别的用电模式，因此，检测模型选用密度峰值（density peaks，DPeaks）聚类算法，使模型可以检测多种类别的电力用户。此外，考虑到位置信息（电力用户的台区号、小区号等）相同的电力用户往往有着相似的用电模式，且这些信息比较容易获取，本文在维度规约中使用线性判别分析（linear discriminant analysis，LDA）方法计及了电力用户的位置信息。最后，为降低参数的选取难度，设置了电力负荷异常检测的双判据。使用本模型对爱尔兰智能电表数据进行了检测，验证了该方法的有效性。

1 DPeaks 聚类算法原理

DPeaks 聚 类 算 法 由 Alex Rodriguez 和Alessandro Laio 于2014 年提出［21］，是一种基于密度的聚类算法，可以识别任意簇型且聚类过程所需参数较少［22］。对于每一个数据点i，DPeaks 聚类算法需要计算2 个量：点i的局部密度（下文简写为密度）ρi和点i与最相邻的更高密度点的距离（下文简写为距离）δi。点i的密度定义为：

密度最高点的距离取两点之间的最大距离。

基于各个点的密度ρ和距离δ，采用DPeaks 聚类算法绘制出δ-ρ决策图并将所有点分为3 种类型：密度峰值点（即聚类中心）、正常点和异常点。算法原理见附录A 图A1。密度峰值点位于决策图的右上方，ρ和δ均较大，邻域内有很多点但没有比其密度更大的点；正常点位于决策图的下方，δ较小，邻域内有比其密度更大的点；异常点位于决策图左上方，ρ较小且δ较大，邻域内没有除自身以外的点存在。算法流程见附录A。

2 异常检测模型

基于LDA 和DPeaks 聚类算法的无监督电力负荷异常检测模型整体框架如图1 所示。

图1 所提模型的整体框架Fig.1 Overall framework of proposed model

2.1 特征构造

特征构造可以挖掘原负荷数据的深层信息，提高异常检测模型的准确度。本模型基于用户的日、月用电量数据构造了其形态、波动性、趋势性和相关性指标。

2.1.1 形态指标

1）日、月平均用电量；

2）日、月用电量率，即平均用电量与最大用电量的比值；

3）月用电量峰谷差率［23］，即最大最小用电量的差值与最大用电量的比值；

4）每季度用电量占全年用电量的比例。

2.1.2 波动性指标

1）日、月用电量离散系数［24］，即日、月用电量标准差与日、月用电量均值的比值；

2）日、月用电量离散系数与行业日、月用电量离散系数的比值［24］（用所有用户用电量的平均值代表行业用电量）；

3）前后m个月用电量的首尾差值。

2.1.3 趋势性指标

1）日用电量序列线性拟合的斜率k；

2）月用电量序列的上升趋势和下降趋势［13］。

2.1.4 相关性指标每户日用电量序列与典型日用电量序列（用所有用户日均值序列表示）的皮尔逊相关系数。

2.2 维度规约

构造的特征数量较多且可能包含相关性强的特征，为方便数据可视并提高算法效率，有必要对特征集降维处理。常用的降维方法有主成分分析（principal component analysis，PCA）和LDA。本文选用LDA 对原特征集降维，LDA 是一种有监督方法，即需要已知数据的类别信息。需要特别指出的是，本文模型中LDA 输入的数据类别信息是电力用户台区标签，而非异常用户标签，因此，本文整个电力负荷异常检测模型依然是无监督模型。利用数据标签，可以使降维后同一类别的数据更紧凑［25］，使聚类算法倾向于将相同台区的用户归为一类。

为确定新特征的维度，使用累积贡献率来反映降维数据中所包含的原始数据信息的多少。累积贡献率通常要达到85%才能较为全面地表达出原始数据信息［26］。需要注意的是，PCA 降维后的维度可以达到原数据的维度，而LDA 降维后的维度最多为标签类别数减1。单个特征的贡献率和累积贡献率的计算公式如下：

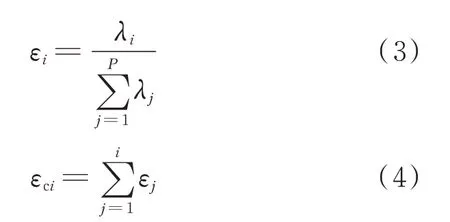
式中：εi为第i个特征值的贡献率；λi为第i个特征值；P为新特征值的总个数；εci为前i个特征值的累积贡献率。

2.3 异常值判定标准

聚类算法多用于解决分类问题，对于异常检测问题，有必要明确异常值的判定标准。DPeaks 聚类算法在异常检测时，往往只设置单个异常值判据［27-28］。本文根据DPeaks 聚类算法原文异常值的识别原理，分别基于δ-ρ决策图和数据点的实际坐标设置了识别异常值的2 个判据。

位于δ-ρ决策图左上方的点为异常点，由此给出第1 个异常点的判据。

判据1：如果某个数据点的密度ρi小于基准密度ρ0且距离δi大于基准距离δ0，那么这个点是异常点。各个簇的基准密度和基准距离的计算公式如下：

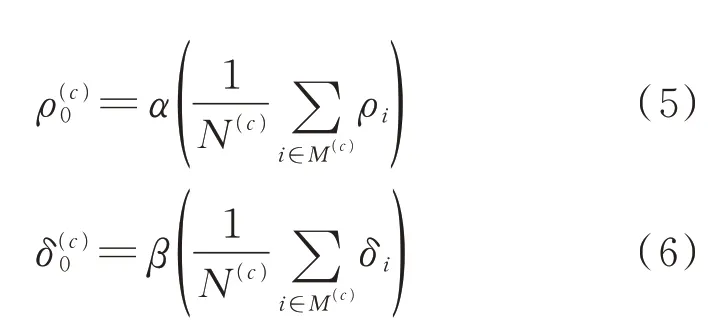
式中：ρ(c)0、δ(c)0分别为第c个簇的基准密度、基准距离；α、β为经验常数；N(c)为第c个簇包含的数据点的总个数；M(c)为第c个簇包含的数据点集合。

实际坐标越远离聚类中心的点越可能是异常点，由此给出第2 个异常点的判据。

判据2：如果某个数据点的密度ρi小于这个点所属簇的边界密度ρb，那么这个点是异常点。

本文定义分别属于不同簇且欧氏距离小于ω倍的dc的2 个点分别为这2 个簇的边界点（有很多组边界点）。由边界点可以求取各个簇的边界密度ρ(c)b（上标c表示簇号），求取过程如下：

步骤1：令所有簇的边界密度ρ(c)b的初值为0；

步骤2：将满足边界点条件的2 个点的平均密度作为这2 个点所属簇的边界密度；

步骤3：重复步骤2 得到所有簇的多个边界密度；

步骤4：取每个簇中的最大边界密度作为这个簇最终的ρ(c)b。

参数α、β决定判据1 的严格程度，α越小、β越大则模型依据判据1 检测出的异常值越少；参数ω决定判据2 的严格程度，ω越小则模型依据判据2 检测出的异常值越少。双判据模型将同时满足上述2 个单一判据的点判定为异常点。

为方便对检测结果进行评估，本文给出数据点基于判据1、判据2 的异常概率P1、P2和基于双判据的异常概率P：

式中：ρmax为所有数据点的最大密度；δmax为所有数据点的最大距离。

异常概率仅在用户间才有相对意义，只用于计算模型的曲线下方包围的面积（area under curve，AUC）指标，不作为异常数据的检出依据。

2.4 模型评价指标

本质上，电力负荷的异常检测是一个类别不平衡的二分类问题，不能使用以准确度为依据的评价指标，因为即使分类器将全部用户识别为正常用户，也可以获得较高的评价。电力负荷异常检测模型的优劣常用受试者工作特征（receiver operating characteristic，ROC）的AUC 指标来评价。AUC 的求取需要先获取二分类器的混淆矩阵。

2.4.1 混淆矩阵

混淆矩阵包含了一个二分类器所有可能的分类结果，如表1 所示。

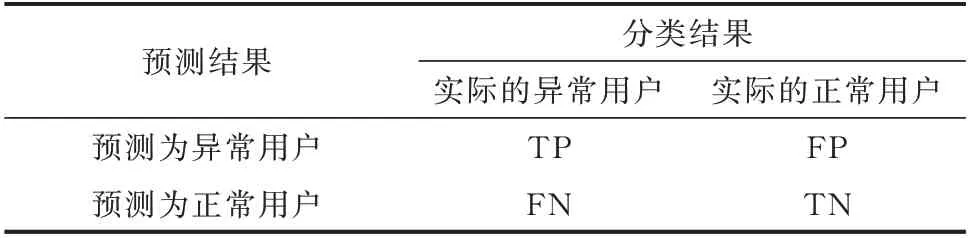
表1 用于电力负荷异常检测的混淆矩阵Table 1 Confusion matrix applied in anomaly detection for power load

式中：ATP表示分类器预测为异常实际也是异常的用户数量；AFN表示分类器预测为正常而实际是异常的用户数量；R表示正确检测出的异常数据个数占异常数据总数的比例。召回率R越大，分类器性能越好。

2）精确率P：

式中：AFP表示分类器预测为异常而实际是正常的用户数量；P表示正确检测出的异常数据个数占全部检测出的异常数据个数的比例。精确率P越高则误检率越低，分类器性能越好。

2.4.2 ROC 曲线和AUC 指标

根据混淆矩阵可以计算分类器的真阳率（true positive rate，TPR）和假阳率（false positive rate，FPR），分别用于反映检出率和误检率，不同的阈值对应不同的TPR 和FPR 数值。ROC 曲线以FPR为横轴、TPR 为纵轴，反映了不同阈值下检出率和误检率之间的权衡［29］。

AUC 指标的取值范围为［0，1］，AUC 数值越大，ROC 曲线就越靠近最佳分类点（0，1），分类效果越好。

3 算例分析

3.1 数据介绍

本文数据使用爱尔兰智能电表数据集［30］，包含6 445 个电力用户536 d 的用电量数据（单位为kW ⋅h），采样频率为每30 min 一次。存在异常用电行为的用户已被标出，共计205 户。异常用户标签仅作为模型评估的依据，不在检测过程中使用。所有用户来自5 个台区（记为1～5 号），台区号将作为LDA 方法的类别标签。

将每个用户的用电量按天累加，得到536 d 的日用电量数据；为构造能反映长时间跨度下的用电特征，将每30 d 的日用电量数据进行累加，得到18 个月的月用电量数据。数据集中包含一整天用电量为0 的数据点，这在实际中是正常的，但这些数据点会在特征构造时使某些特征值无法求取。本实验将一天用电量为0 的数据点均修改为0.01，用一个很小的值表示用户一天内没有用电的情况。

3.2 实验结果与分析

3.2.1 用户位置信息对模型性能的影响

LDA-DPeaks 模型的检测流程见附录B 图B1。

由用户日、月用电量序列构造的18 个特征分别是：平均日、月用电量F1、F2；日、月用电量序列的离散系数F3、F4；日、月用电量率F5、F6；月用电量序列的峰谷差率F7；第1 年前3 个月和第2 年前3 个月的用电量差值F8；用户日、月用电量离散系数与行业日、月用电量离散系数的比值F9、F10；第1 年中春夏秋冬4 个季度用电量分别占全年用电量的比例F11～F14；用户日用电量与典型日用电量的相关系数F15；日用电量序列线性拟合的斜率F16；上升趋势指标和下降趋势指标F17和F18。

由于以上特征的数量级不尽相同，为平衡各特征对结果的影响，按式（12）对以上特征进行归一化处理。

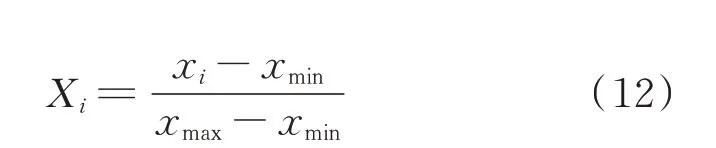
式中：xi、Xi分别为第i个用户的某特征归一化前、后的数值；xmin、xmax分别为该特征的最小、最大值。

考虑到特征F11～F14共同表示全年的用电量形态，将它们乘以权重系数0.25。

18 个特征的相关性分析矩阵见附录C 图C1，其中，F1与F2、F3与F9、F4与F10完全相关，因此将F2、F9、F10删去，保留剩下的15 个特征。

分别采用PCA 和LDA 模型（分别代表忽略位置信息和计及位置信息）将15 个用电特征进行降维处理得到若干新特征，所有新特征根据贡献率依次从大到小排列，表2 截取了贡献率较高的前8 个新特征。当新特征的个数为3 时，PCA 和LDA 降维方法的累积贡献率分别为92.80%、99.48%，均能较好地表示原特征的信息。因此，本实验所取新特征的个数为3。

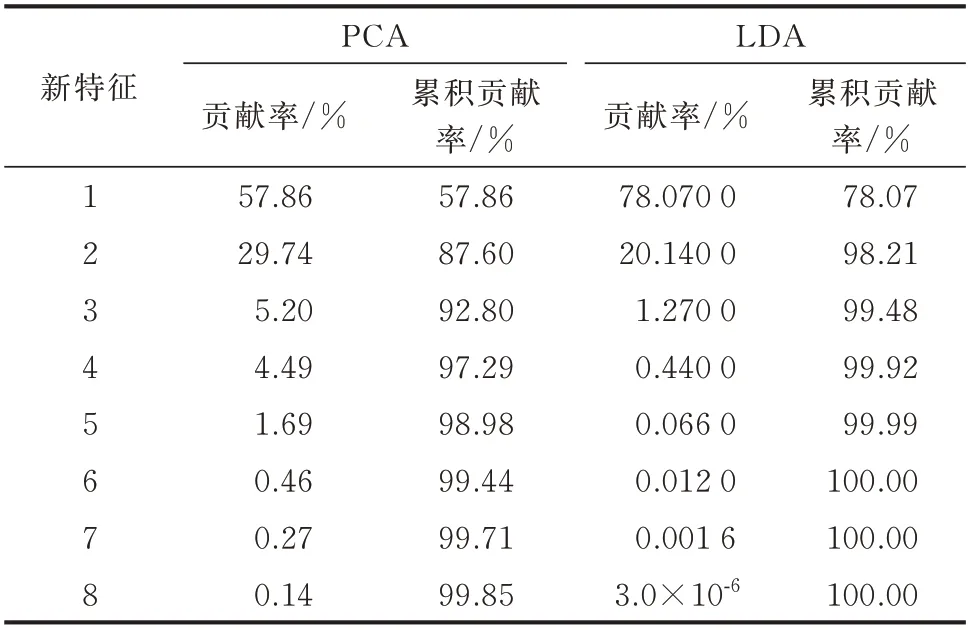
表2 采用PCA 和LDA 模型所得新特征的贡献率和累积贡献率Table 2 Contribution rate and cumulative contribution rate of new features obtained by PCA and LDA models

采用DPeaks 聚类算法对PCA 和LDA 模型得到的新特征数据进行异常检测，检测标准均为双判据。为对比2 类数据的异常检测效果，调整判据的参数使两者检出数量大致相同。PCA 和LDA 模型的α、β、ω参数分别取为0.32、5.0、2.5 和0.35、3.5、38.0。检测结果如表3 所示，2 种新特征均被DPeaks聚类算法分为3 类，两者的异常用户检出总数大致相同，但每一类异常用户数相差较大。检测结果见附录D 图D1、图D2。

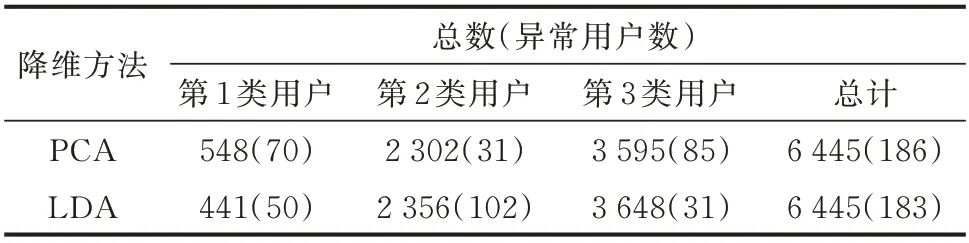
表3 PCA 和LDA 模型的检测结果Table 3 Detection results of PCA and LDA models

一个簇的聚类中心可以表示簇内所有样本的总体特征［31］，因此，将各类别聚类中心用户的用电量曲线作为对应类别的典型用电量曲线。调取PCA和LDA 模型所确定的聚类中心用户的日用电量数据，如图2 所示。PCA 模型确定的第2、3 类别用户的典型日用电量曲线在大部分时间内相互交叉，不利于聚类算法的分簇；LDA 模型的相应曲线大部分时间不存在交叉，2 类用户的类别属性较为明确，有利于聚类算法的分簇。

图2 不同类别典型用户的用电量曲线Fig.2 Electricity consumption curves of different types of typical users

调用数据集的异常用户标签信息，将检测结果与实际异常用户进行对比，见附录D 图D3、图D4。可以看出，LDA 模型比PCA 模型的检出率更高，误检率更低。

在不考虑模型计算速度和可视化的情况下，增加一组PCA 模型取前6 个新特征（PCA 取前6 维和LDA 取前3 维的累积贡献率非常接近）的对比实验，以消除2 种降维方法对原数据的还原程度差异对实验结果的干扰。3 种模型的ROC 曲线如图3 所示（图中括号内的3D、6D 分别表示3 维、6 维），可见LDA 模型具有更高的AUC 指标。

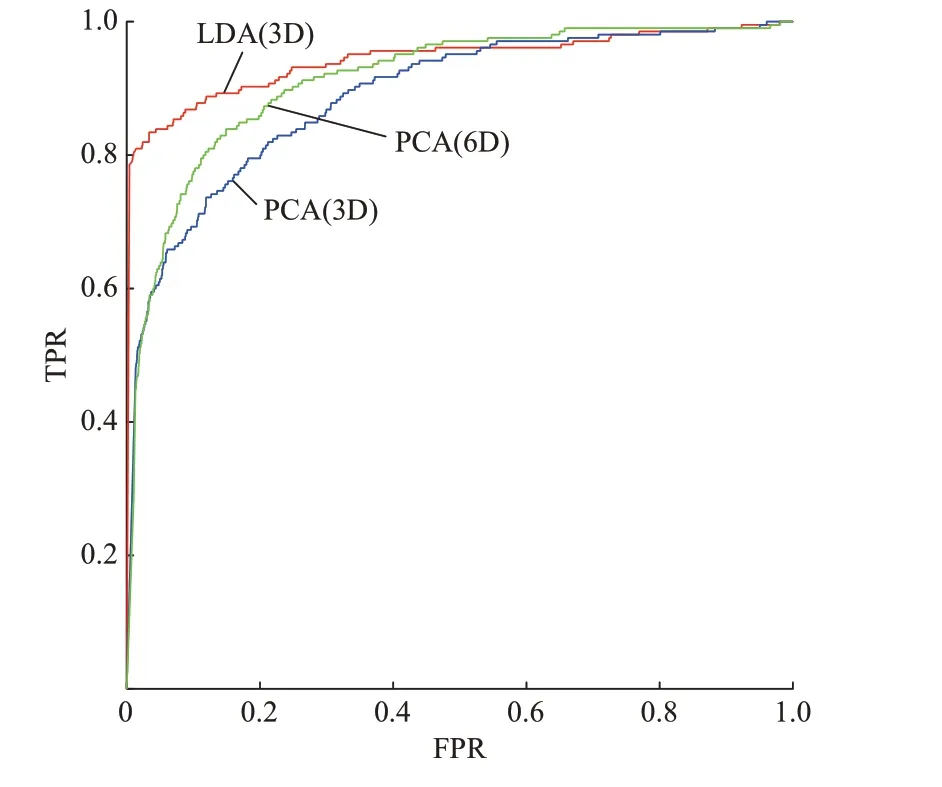
图3 3 种模型的ROC 曲线Fig.3 ROC curves of three models

为消除不同降维方法对实验结果的影响，增加一组以PCA-DPeaks 模型的聚类结果为标签的LDA-DPeaks 模型的实验，表示不考虑位置信息的情况；为测试位置信息对其他聚类算法的影响，增加了3 组DBSCAN 聚类算法的对比实验（DBSCAN算法的ε参数为邻域距离，T参数为ε邻域内所包含的数据点个数的阈值，若某个数据点ε邻域内点的个数小于T，则被DBSCAN 算法识别为异常点）。各模型评价指标如表4 所示。可以发现，考虑用户的位置信息后，DPeaks 和DBSCAN 两种算法的异常用户检出率和精确度都有不同程度的提升。

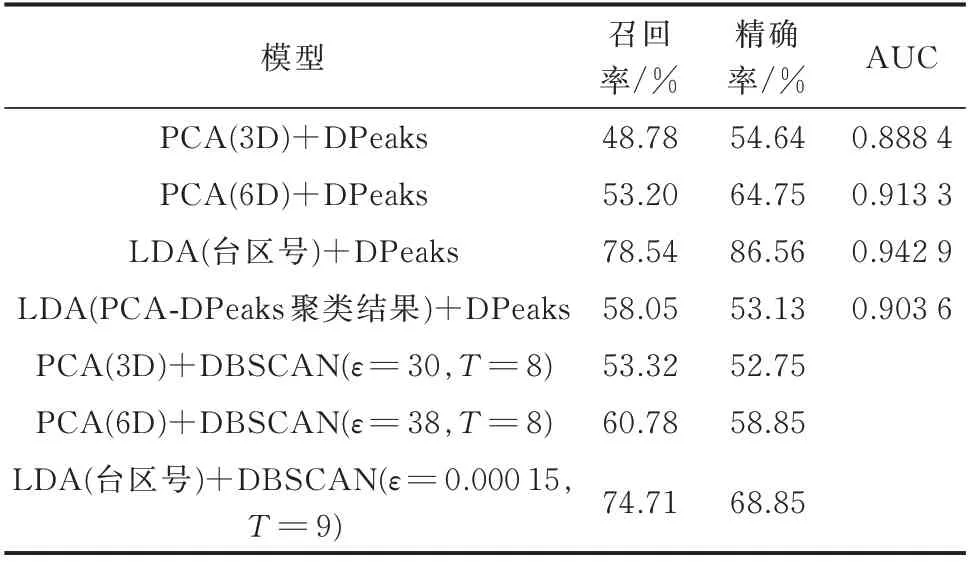
表4 LDA 和PCA 模型性能对比Table 4 Performance comparison between LDA and PCA models

综上所述，考虑用户位置信息的DPeaks 聚类模型可以减少聚类过程中不同类别用户之间的相互干扰，有利于提高模型的检出率和精确度。

3.2.2 参数对模型性能的影响

分别采用基于判据1、判据2 的LDA 模型进行用电量数据异常检测。在决策图中选取了3 个聚类中心，如附录E 图E1 所示。将检测结果按不同类别分别在决策图和实际坐标上标出，2 个单一判据同时检测出的用户为双判据的检测结果，如图4所示。

图4 不同判据下模型的检测结果Fig.4 Detection results of models with different criteria

可以看出，判据1 可以准确识别出决策图基准线左上方的异常用户（图4（a）、（b）、（c）），在决策图上表现良好；而在实际坐标上，判据1 检测第2 类用户时会将靠近簇中心的正常用户误认为异常(图4(e))。判据2 识别出的异常用户大多是用户所属簇边缘的点（图4（d）、（e）、（f）），说明判据2 在实际坐标上的表现较好；而对于决策图左上方的异常点，判据2 表现不佳，在检测第1、2 类用户时误检率较高（图4（a）、（b）），在检测第3 类用户时（图4（c））检出率较低。也就是说，2 个单一判据各有利弊。双判据识别出的异常用户为图4 中2 个单一判据同时标记的用户，兼具2 个单一判据的优势。

将检测为异常用户的异常概率记为1，其余按式（7）—式（9）计算。各判据下模型的基准参数α0、β0、ω0均设为0.35、3.5、38.0，评估指标如表5 所示，3 种判据的AUC 指标均大于0.9，说明3 个判据下模型的异常检测效果都较好。双判据的召回率略低于单个判据，但其精确度远高于单个判据，结合其AUC 指标说明：双判据模型的整体性能优于单个判据模型。

表5 基于不同判据的LDA 模型性能对比Table 5 Comparison of LDA model performance based on different criteria

在α0、β0、ω0的基础上，改变其中一个参数，保持另外2 个参数不变，计算不同参数下模型的AUC 指标。如图5 所示，不合理的β、ω参数分别会导致判据1 模型、判据2 模型的AUC 远低于最佳值，α参数对判据1 模型的AUC 也有轻微影响；但3 个参数的变动对双判据模型的AUC 影响均很小。

图5 各参数对不同判据模型性能的影响Fig.5 Influence of various parameters on performance of models with different criteria

综上所述，双异常值判据的设置使检测结果受参数变化的影响变小，增大了各参数的合理值区间，降低了参数的选取难度（仍需参考经验）。此外，双判据模型异常检测的综合性能也优于单判据模型。

4 结语

本文提出了一种考虑用户位置信息的无监督异常用电检测模型。模型基于聚类算法，可以检测多类别的电力用户；使用LDA 计及了用户的台区信息，使检测出的异常用户更全面、准确；针对不合理参数对模型检测效果的不利影响，设置异常检测的双判据标准，增加了参数的合理取值范围。

本文所提模型的局限性是DPeaks 聚类算法计算复杂度较高（为O（n2）），面对海量负荷数据，计算时间可能过长。后续将针对算法计算效率问题进行改进。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。