基于图卷积网络的微电网拓扑辨识

孙 伟，朱世睿，杨建平，朱梦雨，李奇越

（1. 合肥工业大学电气与自动化工程学院，安徽省合肥市 230009；2. 工业自动化安徽省工程技术研究中心，安徽省合肥市 230009；3. 山东科汇电力自动化股份有限公司，山东省淄博市 255087）

0 引言

微电网是指由分布式发电（distributed generation，DG）单元、储能装置、负荷、控制装置等组成的小型发配电系统［1-2］。微电网稳定安全的运行需要对DG 单元采取合适的控制策略以保证DG单元的功率在运行时保持均衡状态［3-4］。对于某区域内多个小型孤立微电网体系，当某个微电网内部发电功率过剩而相邻微电网功率不足时，可将部分DG 单元在2 个相邻微电网中进行切换以增加微电网的灵活性。但微电网拓扑发生变化也会对其控制性能产生较大影响。及时辨识拓扑结构并根据拓扑结构调整DG 单元的控制策略，抑制因拓扑变化导致的微电网控制问题是变拓扑微电网稳定运行的可行思路［5-7］。

目前，电力网络拓扑辨识方法主要可分为两大类。一类方法是依靠智能测量设备和历史拓扑库，以潮流分析或者传统的数学运算为基础实现拓扑辨识［8-9］。文献［8］提出一种基于配电网数据采集及监视控制系统和微型同步相量测量装置数据融合的电网拓扑辨识方法，通过历史数据库罗列所有可能的拓扑情况，利用遍历对比辨识电网开关状态的变化。文献［9］利用关联矩阵的简化加快网络拓扑的分析速度，提出一种基于邻接矩阵的网络拓扑辨识算法。以文献［8］和文献［9］为代表的这类方法过于依赖历史数据库中拓扑结构的全面性，拓扑辨识的计算效率低且实时性差。

另一类方法是利用人工智能领域中的深度学习技术，运用数据驱动的思想［10-11］。文献［10］利用可用于模式识别的电压序列数据，并设计两层前馈深度神经网络识别电网中开关和保护装置的状态。文献［11］采用一种结合主成分分析和深度置信网络的电网拓扑识别模型，利用主成分分析法中鲁棒特征提取的特点来处理数据和滤除噪声，并使用深度置信网络来捕捉电压幅值和线路开关状态之间的非线性关系。但是此类方法仅是对电网中节点或线路数据的挖掘，并没有考虑电网节点间的结构信息。

针对现有拓扑辨识方法存在的缺陷，本文提出了一种综合节点本身的数据特征和电网结构特征的基于图卷积网络（graph convolutional network，GCN）的微电网拓扑辨识方法。本文首先建立了包含DG 单元的微电网拓扑图模型。然后，将拓扑图转化为描述边特征的线图，以便将微电网结构信息纳入拓扑辨识计算。最后，通过GCN 实现微电网拓扑状态的辨识，并仿真验证了所提方法的有效性。

本文所提方法的创新点在于：1）引入了微电网拓扑图向线图转化的预处理思想，解决了GCN 仅能处理图结构中节点信息的限制与微电网拓扑辨识需要处理图结构中边信息的需求之间的矛盾。2）当微电网中的断路器开关状态变化，且有其他微电网参数（如负载功率变化）时，本文方法依然有很高的拓扑辨识准确率，具有较好的鲁棒性。

1 微电网的拓扑辨识需求与GCN

1.1 微电网控制对拓扑辨识的需求

为了分析微电网控制对拓扑辨识的需求，本文采用如图1 所示的微电网模型。该微电网由8 个DG 单元（DG1～DG8）和相应的负载组成，并通过公共连接点（point of common coupling，PCC）处的断路器与外部配电网相连，K1～K8 为断路器。当PCC 与配电网断开时，微电网处于孤岛运行模式［12］。当微电网孤岛运行时，电网内负荷的功率需求由所有DG 单元共同承担。目前常用的电压频率和幅值下垂控制是一种实现功率均衡的有效方法［13-14］。

图1 微电网模型结构图Fig.1 Structure diagram of microgrid model

然而，当微电网线路出现故障时，继电保护系统会对断路器开关进行控制，导致微电网运行拓扑发生变化。拓扑的改变会导致各DG 单元的控制策略无法满足变拓扑后的微电网稳定运行条件［15-16］。为了说明拓扑变化对微电网的影响，附录A 展示了因发生故障导致微电网运行拓扑改变时，微电网各DG 单元电压和频率的仿真结果。可以看出，为了保证拓扑变化后微电网系统的稳定，需要及时识别线路开关的变化，并修正各DG 单元的控制策略。

由图1 可知，微电网各DG 单元通过线路及断路器连接，当微电网发生故障导致某处断路器的开关断开时，微电网的网络拓扑发生改变，需要实时获取微电网拓扑信息。将图1 中每个DG 单元及对应的负载模块化并抽象成节点，DG 单元之间的线路连接抽象成边，得到微电网模型抽象到数学域上的拓扑如附录B 图B1 所示。

这样，微电网拓扑辨识问题就转化成了图上边的状态的观测问题，边的状态为0 代表对应微电网线路上断路器开关断开，边的状态为1 代表断路器开关闭合。因此，利用微电网DG 单元的电力特征信息，有望通过GCN 强大的图拓扑学习能力得到图上每条边的状态，从而实现微电网的拓扑辨识。

1.2 GCN 的基本原理

GCN 是一种基于图的神经网络，利用直接在图上进行类卷积的操作，解决了常规深度学习方法无法直接处理的非欧氏数据问题［17］。现有的GCN 包括基于谱的GCN 和基于空间的GCN。基于谱的GCN 在谱图理论的框架下提出一种卷积神经网络的表达式［18］，利用图信号处理中的滤波器来定义图卷积，图信号中的噪声可以通过图卷积运算去除［19］；基于空间的GCN 将图卷积定义为来自邻居的特征信息的聚合［20］。

本文采用基于空间的GCN，利用边对节点信息进行聚合从而生成新的特征表示，图中的每个节点都因为邻居节点和更远节点的影响而在改变特征信息［21］。以5 个节点的拓扑图为例，GCN 的结构如图2 所示。图中：hl，i为第l个图卷积层第i个节点的隐藏特征向量，i∈[1，5]；fl为第l个图卷积层的聚合函数，l∈[1，K]，K为网络中图卷积层的总个数；h0，i为第i个节点的输入特征向量；ŷi为第i个节点的最终输出向量。

图2 GCN 结构图Fig.2 Structure diagram of GCN

GCN 的输入包括：1）图中所有节点的输入特征向量组成的N×M维输入特征矩阵X，N和M分别为节点数和节点输入特征向量的维数；2）图的结构特征描述一般用图的邻接矩阵表示，中间经过K个图卷积层后，得到GCN 的输出特征矩阵Z。

在中间K个图卷积层中，节点的特征以隐藏特征的形式在图结构中流动，每一个图卷积层的具体运算表达式为：

2 微电网拓扑辨识方法

2.1 微电网拓扑的抽象

本文的应用场景是通过观测微电网各DG 单元间线路上断路器的开关状态实现拓扑辨识，属于图论模型中边信息的处理。而GCN 的输入、信息汇集以及输出均针对图中的节点信息。图中的边只存储结构信息，并没有实质的特征信息，这从原理上就直接决定了GCN 仅能处理节点信息的限制。为解决上述GCN 仅能处理图结构中节点信息的限制与微电网拓扑辨识需要处理图结构中边信息的需求之间的矛盾，本文将微电网拓扑图中的边抽象成节点，生成一个抽象后的线图拓扑［23］。以图2 中5 个节点的微电网拓扑图为例，将其抽象成线图拓扑的过程如图3 所示。

图3 微电网拓扑抽象成线图拓扑过程Fig.3 Process of abstracting microgrid topology into line graph topology

首先，将原拓扑中所有的边抽象成节点并进行编号。然后，若原拓扑中两条边相邻，则在线图中将它们抽象后的节点之间连接一条边。根据生成的线图，就可以利用GCN 实现边层面的分类任务。

2.2 微电网拓扑辨识相关的节点特征计算

GCN 的输入是图中各个节点的特征。为了进行微电网拓扑的辨识，需要确定和微电网中开关状态相关的各DG 单元的电气量特征。可供选择的电气量有DG 单元输出的电压、电流、频率和功率。经MATLAB/Simulink 仿真发现，当微电网中有开关状态发生变化时，变化时刻前后，各DG 单元的输出电压变化趋势最为明显。因此，选用DG 单元的输出电压来表示微电网的节点特征。

本文将微电网原来的拓扑图转化为线图的形式，所以要将原来的节点特征转化为边的特征。以微电网相邻DG 单元输出电压的差值作为线图中对应节点的节点特征。

2.3 基于GCN 的微电网拓扑辨识算法流程

GCN 在用于微电网的拓扑辨识时，所学习的模型会受到负荷、DG 单元的输出功率以及节点连接关系的影响，这与图像分类有所不同，但是算法流程几乎一致。通过输入图的拓扑信息以及节点特征信息，GCN 会有监督地学习节点特征间的潜在联系，最后得到微电网中所有的开关状态。基于GCN 的微电网拓扑辨识流程如附录B 图B2 所示，具体步骤如下。

步骤1：数据的导入与预处理。首先，导入微电网的拓扑结构、微电网各DG 单元的历史输入电压序列以及微电网各DG 单元间线路上断路器的开关状态。然后，将导入的微电网拓扑图按照图3 所示方法抽象成线图，并将原微电网拓扑中相邻DG 单元的历史输入电压序列作差，作为抽象后线图中对应节点的特征。考虑到GCN 输入节点特征的数据可能差异过大，容易造成GCN 的损失函数难以收敛或者精度不高的问题，采用规范化处理将节点特征的各个分量映射到［0，1］区间如式（2）所示［24］。假设节点特征向量为x，则

式中：xj和x*j分别为规范化前和规范化后第i个节点的特征分量，j∈[1，M]；xmin和xmax分别为节点特征所有分量中的最小值和最大值。

将处理之后的数据样本按一定比例随机分成训练集、验证集和测试集，其中训练集和验证集用来确定GCN 的各种超参数以及权重，测试集用来评估训练完成后GCN 模型的性能。

步骤2：初始化GCN 的结构和参数。在开始训练GCN 之前，需要设置GCN 的网络结构和参数，例如图卷积层的个数、优化器、损失函数等。GCN 的网络结构和超参数见附录B 表B1。

步骤3：训练GCN。首先，输入抽象后线图的边集、点集以及各节点特征，得到线图的邻接矩阵A和节点特征矩阵X。然后，通过多个图卷积层及批归一化（batch normalization，BN）操作来实现节点特征信息的汇集及标准化过程，提取并学习节点电压差之间的特征，由Softmax 层输出分类后的状态向量，其中的每一个分量代表对应断路器的开关状态。最后，利用观测值与真实值通过式（3）中的交叉熵损失函数计算所有节点总的损失函数值，并利用反向传播算法更新GCN 的权重［25］。经多次迭代满足终止条件（达到迭代次数或损失函数值小于一定的阈值），表明GCN 学习到了数据间的映射规律，将此时的GCN 模型保存。

式中：LC为图中所有节点总的损失函数值；ym为第m个节点的真实值；y͂m为第m个节点的观测值。

步骤4：GCN 模型的评估。将测试集的节点电压差序列输入已经训练好的GCN 模型中，用于实时的断路器开关状态观测，以获得微电网的拓扑结构。

3 仿真分析

3.1 样本采集

为了测试所提微电网拓扑辨识方法的性能，本文通过MATLAB/Simulink 仿真获取微电网DG 单元的输出电压。其中部分微电网DG 单元节点的输出电压数据如附录B 图B3 所示。根据微电网拓扑计算相邻DG 单元的输出电压差数据。并设置T=0.01 s 的采样周期对电压差进行采样，获取输出电压差在采样点处的离散值。

微电网线路上断路器开关状态设置方面，在初始时刻，将所有开关均闭合，之后每隔2 s 选择其中1 个开关断开；所有开关均断开1 次后，再每隔2 s 选择其中2 个开关断开。根据每次开关切换后的微电网数据构造样本集，取开关切换时刻前后各10 个采样点的电压差离散值组成电压差时间序列，作为对应微电网线图拓扑的节点特征，节点的标签取对应线路的开关状态，闭合标注为1，断开标注为0。然后，将构造的样本集按分层采样的方式分为训练集、验证集和测试集，比例为7∶2∶1。样本集的具体内容如包含的节点数、边数、属性数以及类个数见附录B 表B2。

3.2 仿真结果及分析

3.2.1 辨识准确度测试

为了直观地了解GCN 的稳定性、收敛速度以及准确度，附录B 图B4 和图B5 分别展示了随着迭代次数的增加，训练集和验证集的损失函数和准确度的变化。

由附录B 图B4 可知，随着迭代次数的增加，训练集和验证集的损失函数值迅速下降。当GCN 经过80 次迭代后，损失函数值已经趋于平稳不再继续下降，说明此时的GCN 已经收敛，对输入拓扑节点特征和结构特征的学习已经基本完成。进一步对比训练集和验证集的损失函数的变化，发现它们之间的下降趋势和最终稳定值比较相近，这说明GCN 具有较强的泛化能力，没有出现过拟合的现象。由附录B 图B5 可知，训练集和验证集的准确度随着迭代次数的增加迅速升高并达到稳定值，训练集和验证集的准确度最终分别稳定在0.955 和0.925 左右，说明GCN 的特征提取和学习效果良好。

为了分析GCN 中图卷积层的个数对GCN 性能的影响，本文从1 层开始逐渐增加图卷积层的个数至4 层，使用同样的样本集对其训练，并统计验证集的准确度如图4 所示。

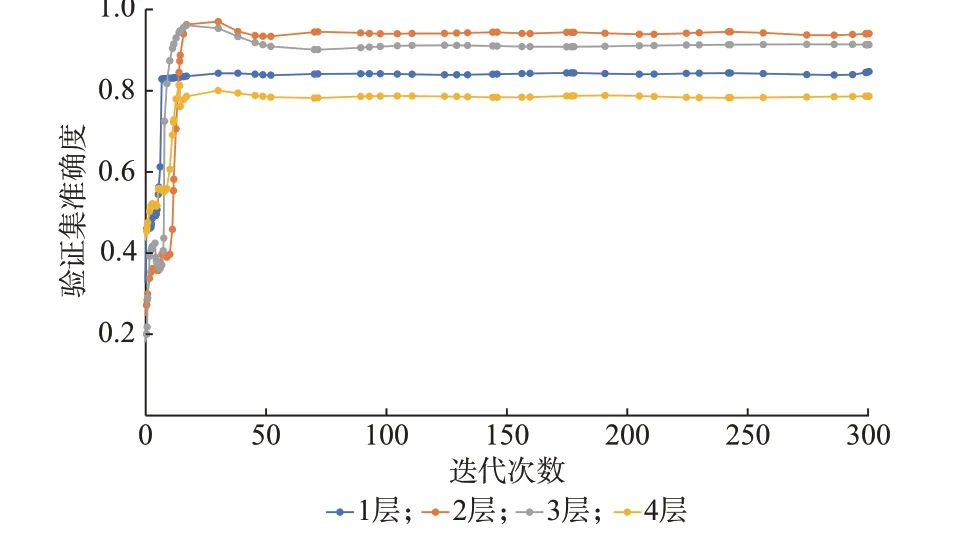
图4 不同图卷积层数下验证集的准确度Fig.4 Accuracy of validation set in different numbers of graph convolutional layers

根据图4 所示的准确度曲线可知，图卷积层数为1 时，GCN 便已经有了较强的辨识性能，但节点特征信息汇集的深度不够。当图卷积层增加至2 层时，验证集的准确度最高，此时GCN 的性能最佳。而当图卷积层数大于2 时，继续增加层数会导致GCN 的性能变差，一方面是由于数据集的样本个数有限，过多的图卷积层会增多GCN 待训练的参数，容易出现过拟合现象；另一方面是由于本文应用场景微电网中节点个数不多，分支较少，所以GCN 层数过多会导致信息汇集出现交叉，从而使图中所有节点特征趋于一致，降低了拓扑辨识的精度。因此，在微电网结构较小、训练样本较少的情况下，设置图卷积层为2 层便可以获得较高的拓扑辨识性能。

为了验证GCN 模型的优越性，将其与较为先进的几种电网拓扑辨识方法如支持向量机（support vector machine，SVM）、贝叶斯网络（Bayesian network，BN）、轻量梯度提升机（light gradient boosting machine，LightGBM）、随机森林（random forest，RF）进行了对比［26］，得到各种方法测试集的准确率和计算时间如表1 所示。

表1 不同方法下电网拓扑辨识的性能Table 1 Performance of power grid topology identification with different methods

在表1 所示的5 种电网拓扑辨识方法中，本文所提GCN 模型的测试准确率最高并且辨识的时效性也最佳，计算时间比其他的方法少了一个数量级以上。这是因为GCN 可以直接在图上进行运算，且仅需要较少的网络层数便可以实现图上信息的有效学习，这说明GCN 在电网拓扑辨识方面的性能优于其他数据驱动的方法。

3.2.2 辨识鲁棒性测试

为了验证所提方法在微电网其他参数可变的情况下依然有效，测试拓扑辨识的鲁棒性，本文模拟微电网真实运行情况，将微电网中DG 单元的负载功率由定值调整为随时间振荡，时间间隔以5%的步长在额定功率的50%～90%之间变化。重新构造样本集对GCN 训练和测试，得到在负载功率时变情况下微电网拓扑辨识的准确度如附录B 图B6 所示。

由附录B 图B6 可知，在微电网中的负载功率为时变的情况下，GCN 仍然有比较好的辨识效果，训练集和验证集的准确度虽然比负载功率固定时略低，但仍能保持在0.9 左右，保证了相对良好的辨识效果。这是因为选取的节点特征是微电网相邻DG单元的电压差，当有负载功率等外部因素发生变化后，虽然每个DG 单元的电压会发生一定的变化，但是相邻DG 单元的差值基本保持不变，很大程度上抑制了扰动的影响，因此本文方法在微电网拓扑辨识时具有良好的鲁棒性。

4 结语

为了提升微电网拓扑辨识的准确性和时效性，本文引入图深度学习的思想，提出了一种基于GCN的微电网拓扑辨识方法。结合对GCN 的拓扑辨识的性能分析以及与其他方法的对比测试，得出如下结论：

1）GCN 综合考虑了节点信息以及节点之间拓扑关系的影响，通过节点间信息的汇集能够深入学习到节点特征和结构特征。当微电网线路上断路器的开关发生变化时，GCN 能够精确辨识到拓扑的变化。由于GCN 能够直接对图结构的数据进行处理，因此，本文方法在拓扑辨识方面的性能显著优于SVM、BN 及RF 等其他模型。

2）在微电网运行过程中，除了断路器的开关会发生变化外，负载的功率也会随时间变化。GCN 能够有效抑制因负载功率变化引起的节点特征的扰动，仍然保持着较高的拓扑辨识准确率，体现了本文方法在微电网拓扑辨识时有着较强的鲁棒性。

本文对图深度学习在微电网拓扑辨识中的应用进行了初步研究，后续研究工作可以尝试通过改进节点特征、优化网络结构以及针对不同应用场景引入注意力机制，有利于拓扑辨识精度的进一步提升。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。