具有储能作用的用户侧资源运行特性

赵建立，汤卓凡，王桂林，陈宇扬，王隗东，陈珂，吴英俊

（1.国网上海市电力公司，上海 200030；2.上海市智能电网需求响应重点试验室，上海 200030；3.河海大学能源与电气学院，南京 211100；4.中国电力科学研究院有限公司需求侧多能互补优化与供需互动技术北京市重点试验室，北京 100192）

0 引言

随着近年电力负荷的增加，供给侧的电力调控潜能已捉襟见肘，加之我国提出“双碳”目标使得调控更加困难。因此，在供给侧手段难以满足功能需求的情况下，研究负荷侧用户资源在平衡供需压力中的潜力显得十分重要［1］。

在负荷侧用户资源中，具有储能作用的用户负荷是一类特殊资源，包括铅酸蓄电池、飞轮储能、电动汽车等既有供能特性又有用能特性的供用能负荷［2］。这类资源具有负荷与电源的双重特性，当电网电力过剩时，可利用这些供用能资源存蓄电能；电网电力不足时，这些资源又可以向电网提供电能。供用能资源可以提高资源利用率和平衡电网负荷，缓解供需平衡压力，使电网运行更加经济、安全和稳定。因此，研究具有储能作用的用户负荷具有深远意义。

目前，国内外关于储能技术的研究已取得丰硕成果，许多技术已日趋成熟并投入市场实现了规模化应用。根据储能方法的不同，储能可分为物理储能、化学储能和电磁储能［3］。电力系统领域对储能装置的基本要求是存储容量大，现有的储能技术在满足这一要求的同时，往往对储能装置的选址有较高的要求，只有电化学储能才能同时满足这两种要求，因此电化学储能顺理成章地成为现阶段最热门的研究对象。文献［4］对物理储能技术的发展历史进行了阐述，说明其技术的成熟性，但同时表示物理储能技术存在受周边环境和地理位置影响大、建设成本高等缺点，使得其发展进入瓶颈期。文献［5］介绍了几种目前常见的电化学储能技术及各自特点。文献［6］考虑到电池复杂的降解回收，研究了一种结合可再生能源的电池储能系统最佳容量确定方法。文献［7］调查了安装在变电站中的飞轮储能系统提供调峰服务的情况，通过最小化变压器功率限制违规和飞轮能量损失，制定了飞轮功率设定优化方案。文献［8］提出了连接到单母线聚合电力系统的飞轮储能系统的集成传递函数，实现了飞轮储能系统的最佳动态性能。文献［9］着眼于电磁储能，介绍了其储能原理、应用领域和未来的发展前景。文献［10］通过对家用电动汽车进行可控充电，减小了电力系统平衡供需两侧不确定性，缓解了电力系统急需更多储能的压力。文献［11］对过去20 年电动汽车模式的进展和研究发展进行了全面的回顾，从应用角度出发，研究了每种电动汽车模式类别的发展情况。

本文基于目前已有的研究，选取典型的具有储能作用的用户侧资源，分别对其进行物理仿真建模。结合仿真数据，分析了这些负荷的运行特性，为后续研究奠定了基础。

1 典型供用能负荷模型

选取蓄电池、飞轮储能和电动汽车3 类典型的具有储能作用的供用能负荷，分别建立3 种负荷的供用能模型。

1.1 蓄电池

1.1.1 蓄电池充电模型

蓄电池充电方式多为定电流、定电压二段充电方式［12］。蓄电池在充电时，其端电压、电流与充电时长存在一定的物理联系。通过描述蓄电池充电时3个参数间的关系，得到其充电功率模型

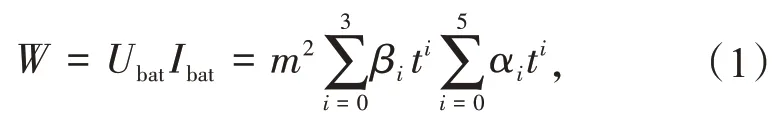
式中：W为充电功率，W；m为蓄电池组的个数；αi为蓄电池充电电流系数；βi为蓄电池充电电压系数。αi和βi统称为充电系数，不同规格的蓄电池，由于其生产厂家和生产技术不同，因此充电系数也不同。

1.1.2 蓄电池放电模型

在蓄电池的放电模型中，荷电状态（SOC）被用作衡量蓄电池的剩余容量，在数值上SOC 定义为蓄电池的剩余容量占其完全充电后容量的比值，取值范围是0～1，其值为1 时，蓄电池为满充状态。SOC的计算公式为［13］

式中：A为铅酸蓄电池有电活性的面积，cm2；t为放电时间，s；Qmax为蓄电池最大容量，kW；I0为蓄电池额定放电电流，A；c为铅酸蓄电池有电活性的物质密度，g∕cm³；cref为铅酸蓄电池最初有电化学的物质密度，g∕cm³；F为法拉第常数，C∕mol；R为蓄电池的内电阻，W；T为温度，K；η，γ，αa，αc为蓄电池参数。

蓄电池在放电过程中，电压会随放电时间延长而逐渐降低，进而形成端电压与时间的放电曲线，其电压变化计算公式为

式中：n为蓄电池组个数；c10为蓄电池10 h 放电率放电容量，kW；I10为10 h 放电电流，A；二者之间的换算关系为I10=0.1c10；ck和dk为蓄电池的放电系数，不同厂家不同型号的蓄电池，放电系数不同；Ixi为蓄电池放电电流，A。

蓄电池放电功率Wd的表达式为

1.1.3 蓄电池储能损耗模型

铅酸蓄电池的损耗一般是指蓄电池的寿命损耗。铅酸蓄电池的寿命与多种因素有关，包括温度、峰值电流、充放电循环和放电深度等［14］，其中对寿命影响最大的因素为该电池的放电深度（Depth of Discharge，DOD），DOD 数值越大则蓄电池寿命越短。因此，为了简化计算，仅考虑放电深度对铅酸蓄电池寿命的影响，建立蓄电池储能损耗模型。

通过雨流计数法可以精确计算出蓄电池的循环周期，结合四阶函数拟合循环寿命与放电深度的关系［15-16］为

式中：N为蓄电池在某一放电深度的充放循环寿命；DOD为蓄电池的放电深度。

1.2 飞轮储能

飞轮储能系统基本结构由飞轮转子、轴承、电动机∕发电机、电力电子控制装置、真空室等5 个部分组成。相较于其他技术，飞轮储能的特点在于几乎无摩擦损耗、风阻小；比功率可达8 kW∕kg 以上，远高于传统电化学储能技术；其寿命主要取决于飞轮材料的疲劳寿命和系统中电子元器件的寿命。

1.2.1 飞轮储能充放电模型

飞轮储能系统主要由功能元件、连接及支撑元件和其他附加设备等组成，功能元件为飞轮、电力电子系统、电动机∕发电机等；连接及支撑元件为真空室、轴承支撑系统、备用轴承等［17］。在用电谷期，飞轮储能系统运行在充电模式下，从电网吸收电能，通过转速增加，将能量以机械能的形式储存在飞轮系统中，直到达到转速的峰值。在用电高峰期，飞轮储能系统调整为放电模式，通过降低转速，逐渐将所储存的机械能转化为电能，返还给电网系统，降低电网供电压力。因此，飞轮储能系统的运行状态可以分为3种情况，即充能加速状态、放电减速状态和空载状态。其储存能量计算公式为

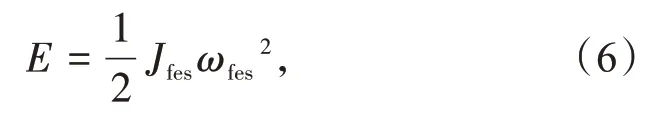
式中：Jfes为转子的转动惯量，kg·m2；ωfes为飞轮转子转速，r∕s。

飞轮储能系统可释放或储存的能量ΔE为

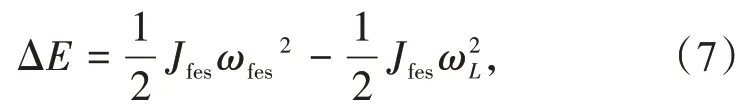
式中：ωL，fes为飞轮储能系统在充放电循环中设定的最低转速，rad∕s。通常情况下，最高额定转速ωH是最低额定低转速ωL的2 倍，即ωH=2ωL。当ωH=ωL时，飞轮达到设计的最大储能量

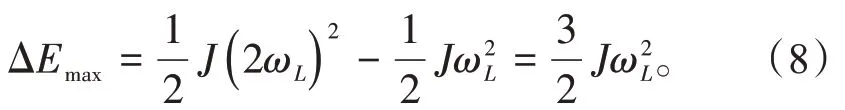
由式（7）可见，飞轮转速是飞轮储能性能的关键影响因素。因此，为了提高飞轮的储能性能，可以增加飞轮的旋转速度。但是，由于工艺水平的限制，大功率高速飞轮的制造难度大、造价高昂，在工程实践中很少运用。目前广泛使用的飞轮储能系统主要为10 000 r∕min以下的钢转子储能系统。

除了提高飞轮转速以外，增加飞轮的转动惯量是另一种增大飞轮储存的能量行之有效的手段

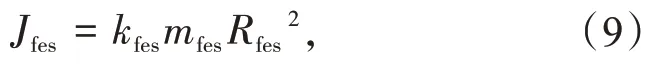
式中：kfes为飞轮材料系数；mfes为飞轮转子质量，kg；Rfes为飞轮转子的半径，m。

能量利用率是衡量储能系统优劣的标志之一，飞轮储能系统的能量利用率与自身所储存能量的最大值和可释放的能量有关，具体如下式所示

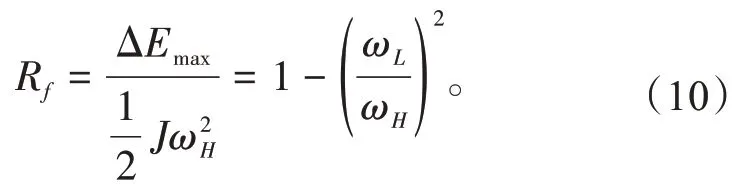
飞轮储能系统的功率P可表示为

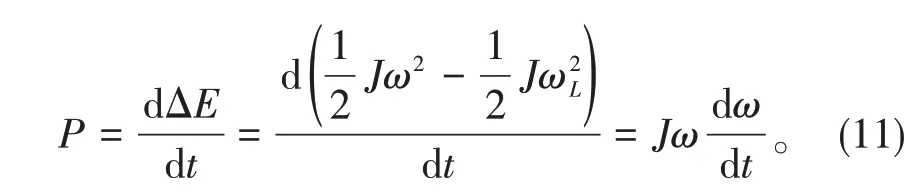
1.2.2 飞轮储能损耗模型

飞轮储能损耗一般分为2 种：摩擦损耗和涡流损耗。现代飞轮储能系统一般都工作在真空环境中，摩擦损耗很小，因此飞轮储能损耗主要为涡流损耗。根据文献［16］，可得飞轮储能的损耗模型如式（12）—（15）所示

式中：Pfwc为涡流损耗，kW；PFe为转子铁心损耗，kW；Pel为除铁心外其他部分涡流损耗，kW；Ph为磁滞损耗，kW；Pcl为经典涡流损耗，kW；Pex为异常损耗，kW；Kh为磁滞损耗系数；fm为交变磁场频率，Hz；Bm为磁密幅值，T；K（Bm）为因局部磁滞环引起的损耗增加系数；B（θ）为硅钢片磁通密度，T；Kcl为经典涡流损耗系数；Kex为异常损耗系数；T为周期，s；R1，R2分别为圆环的内径和外径，m；h为圆环的轴向长度，m；JZ为圆环内的涡流，s-1；σ为圆环材料的电导率，S∕m。

1.3 电动汽车

考虑到用户将电动汽车接入电网充电的行为在时间和方式上均具有不确定性［18］，因此根据电动汽车是否与电网存在能量交互和信息交流（即用户与电网进行信息交流，从而避开电网峰荷进行充电，在负荷高峰期进行放电），建立3 种电动汽车的充放电模型，即无约束充电模型，受控充电模型和基于峰∕谷期的受控充∕放电模型。

1.3.1 电动汽车无序充电情况

无序充电模型是指电动汽车根据实际需要进行非受控充电，且不在高峰时段向电网传输电力，具体建模思路如下。

首先需确定电动汽车充电开始时刻t0，假设t0时刻后电动汽车不再出行，根据美国国家公路交通安全管理局的统计数据，t0满足正态分布。单台电动汽车达到满充状态所需时间可表示为当日行驶距离和充电功率的函数。同样根据统计数据可知，电动汽车日行驶距离满足对数正态分布［10，14］。根据函数关系可推导出充电时间的概率分布和概率密度函数，进一步得出单台电动汽车充电功率需求的函数分布。

式中：tsc为开始充电时刻；T为充电时长，h；F为tsc和T的联合概率分布函数，这里假定随机变量tsc和T相互独立。单台电动汽车在某时刻的充电功率需求为

1.3.2 电动汽车受控充电模型

电动汽车受控充电是指电动汽车在与电网有信息交互的基础上，其被控制在电网负荷的低谷期进行充电，但不反向传输电能给电网。

电网首先会对每日负荷低谷时段进行预测，之后下发给用户。当电动汽车用户所需要的充电时长小于负荷低谷持续的时间，则电动汽车用户可以选择低谷期的任意时段进行充电；而当电动汽车用户所需要的充电时长大于负荷低谷的持续时间，则电动汽车用户只能选择在负荷低谷的起始时间同步开始充电，直到低谷期的结束。其表达式为

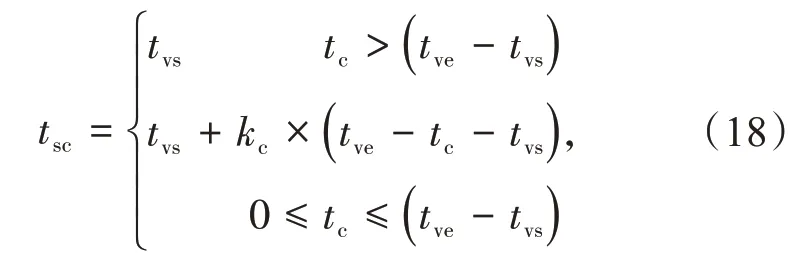
式中：tsc为开始充电时刻；tvs和tve分别为谷期开始和结束的时间（以00：00—07：00为电网负荷低谷期）；tc为充电时长，h；kc为［0，1］区间内的随机数。

1.3.3 基于峰谷期的电动汽车受控充∕放电模型

基于峰谷期的电动汽车受控充∕放电模型，由于与1.3.2节中的充电模型类似，因此不再赘述，其放电模型则需要考虑以下3方面。

（1）针对实际出行中的午高峰（11：00—14：00）和晚高峰（19：00—22：00），为电动汽车设定2 种放电模式，较小的放电功率Pd1对应午高峰；较大的放电功率Pd2对应晚高峰。此外，在午高峰放电时需预留电量以确保车辆的通勤功能。在晚高峰放电时为保护电池寿命，放电后电池电量应不低于20%。

（2）考虑到并不是所有电动汽车用户都能按要求进行放电，特设定用户放电响应度λ，结合车辆实际的日行驶里程统计数据，设定λ=50%。

（3）设定电动汽车在经过午高峰和晚高峰两次放电以后，在电网负荷低谷期进行充电。电动汽车的储能损耗与蓄电池的储能损耗类似，不再赘述。

2 仿真分析

根据第1.1—1.3 节中3 种负荷的仿真模型，分别采用实际物理试验和仿真软件进行测试，并针对试验结果分析3 类负荷的特性。其中，蓄电池使用实际物理试验，飞轮储能与电动汽车仿真模型均运行于Matlab 2012仿真软件。

2.1 蓄电池试验

2.1.1 蓄电池充电

蓄电池在25 ℃的恒温条件下进行充放电，充电方式为恒压充电（电压分别为2.40 V 和2.28 V），充电电流为1.0 A，放电深度控制在50%。经过多次充放电试验，记录试验数据后计算其平均数值，绘制蓄电池充电特性曲线如图1所示。

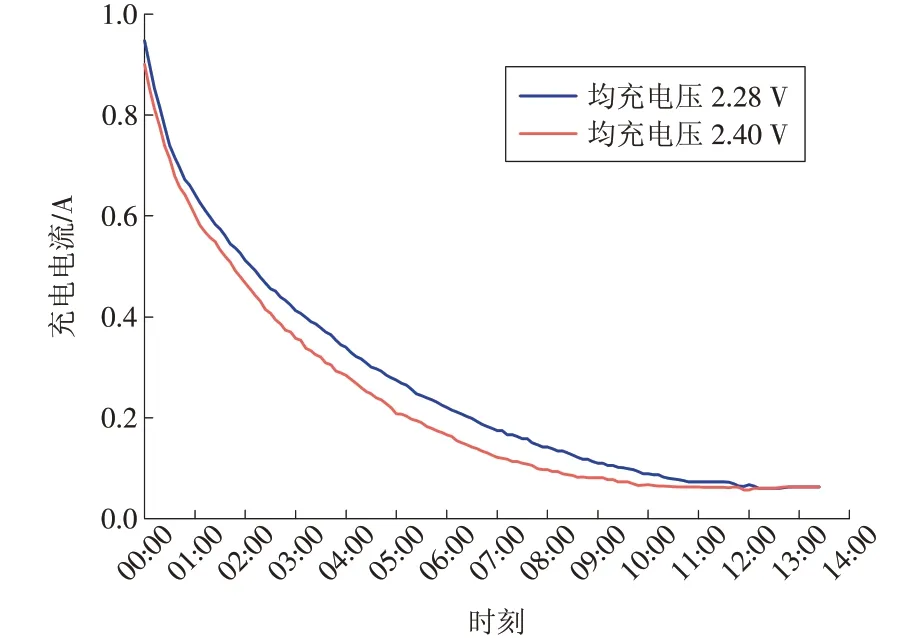
图1 蓄电池充电特性Fig.1 Battery charging characteristics

由图1可见，在恒压充电模式下，充电电流随着充电时间的增加逐渐减小，从0 h 到14 h，充电电流从1.0 A 逐渐降到0.1 A，充电末期的电流已十分微弱，说明充电速度在下降。此外，保持放电深度和充电电流不变，通过改变充电电压，可以观察到蓄电池充满电需要的充电时长几乎相同，均为13 h 左右。因此，在用电高峰期，可以选择使用较低的充电电压对蓄电池进行充电，而不影响充电时长。

通过充放电试验发现工作温度对蓄电池的使用寿命有较大影响。针对储存期内的蓄电池会有电量损失的问题，在蓄电池投入使用前需对其进行一次补充充电。图2展示了某蓄电池工作温度和充电电压的关系。由图2 可见，充电电压随温度升高呈现下降趋势。但是一般情况下规定最低充电电压≥2.2 V，最高充电电压≤2.4 V。

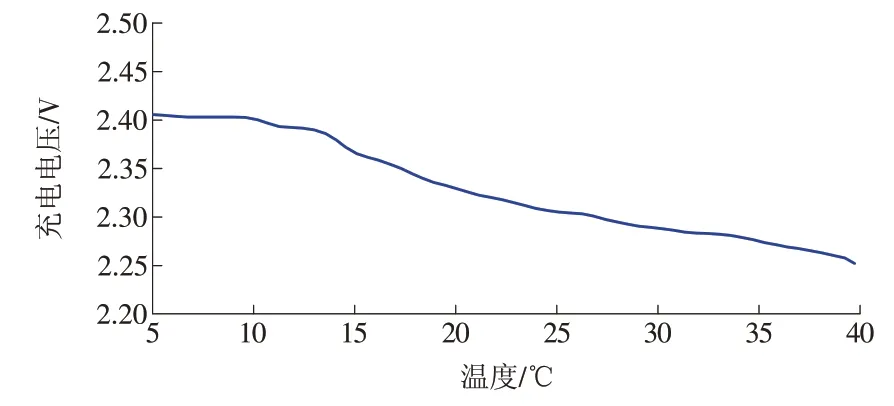
图2 蓄电池工作温度与充电电压关系Fig.2 Relationship between the working temperature and charging voltage of a battery

2.1.2 蓄电池放电

选取2.0 V 阀控密封式铅酸蓄电池作为蓄电池放电仿真的试验对象，放电时间为10 h，通过多次试验，记录数据并绘制放电特征曲线如图3所示。

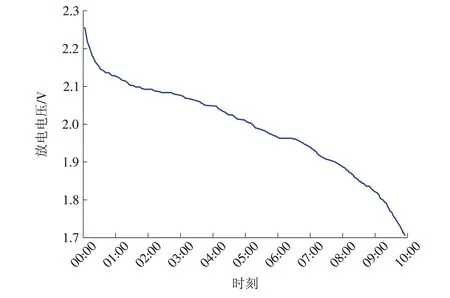
图3 蓄电池放电特性Fig.3 Battery discharge characteristics

由图3 可见，在放电开始时蓄电池的端电压处于急速下降的情况，这是因为蓄电池在刚开始放电时，其极板表面和孔隙中的电解液质量浓度下降速度很快，导致放电速度过高。随着放电持续进行，蓄电池的端电压下降速度开始放缓，虽仍然呈现下降趋势，但曲线斜率较放电开始时已有明显减小，且这一阶段的持续时间很长，约占蓄电池总放电时长的50%以上，保持了蓄电池良好的供电可靠性。随着放电时长逐渐增加，蓄电池处于放电末期时，蓄电池极板表面的电解液质量浓度已降至很低的水平，蓄电池无法再维持稳定的放电速率，端电压急剧下降，直到放电终止。

由于蓄电池的化学特性，其放电容量受到蓄电池周围温度的影响，具体影响关系如图4 所示。由图4可见，蓄电池的放电容量与温度成单调关系，温度越高，放电容量越大，在一定温度范围内近似可看成线性相关，其公式为式中：Ct为蓄电池非基准温度的放电容量，A·h；KT为温度系数（单位温度变化引起的蓄电池容量变化率）；t0为基准温度，一般为25 ℃或20 ℃；t为非基准温度，℃。

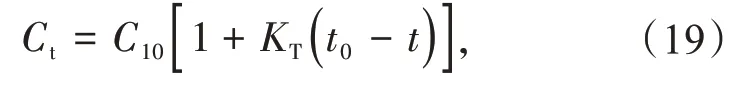
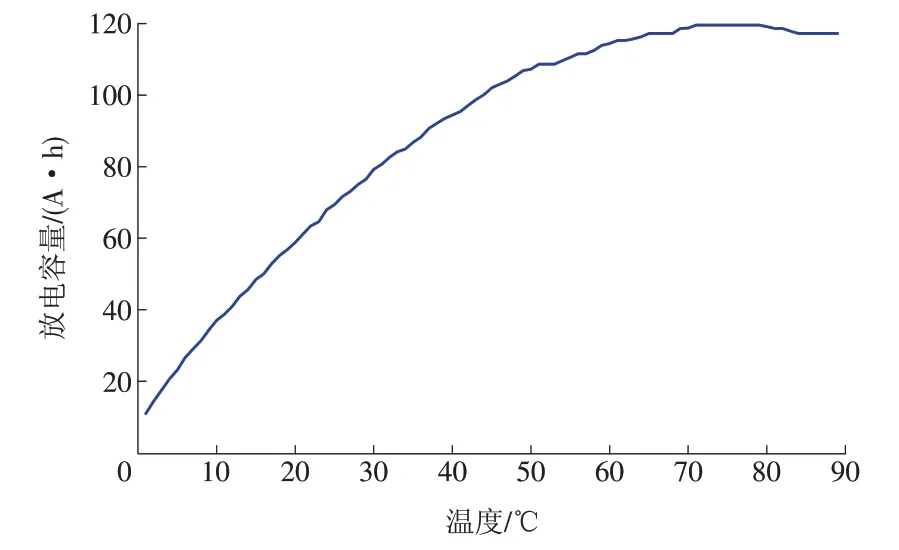
图4 蓄电池放电容量与环境温度关系Fig.4 Relationship between the battery discharge capacity and ambient temperature

2.2 飞轮储能仿真

图5和图6分别为飞轮储能系统功率吸收∕释放功率仿真数据和飞轮转速曲线数据。参数设置为kfes=1.875×10-5，Rfes=2 m，mfes=8 000 kg，功率吸收时长和释放时长均设为90 s。

图5 飞轮系统吸收或释放功率仿真数据Fig.5 Simulation data of the absorbed or released power of the flywheel system

图6 飞轮转速曲线Fig.6 Speed of the flywheel

由图5 及图6 可见，飞轮在0—90 s 处于充电状态，持续从外界吸收能量，转速从2 200 r∕min升高至5 200 r∕min，充电功率保持1 400 kW 不变；在90 s 之后，飞轮结束充电，开始调整为放电模式，其转速逐渐从峰值5 400 r∕min 逐渐回落至2 200 r∕min，放电功率同样保持为1 400 kW，放电持续时长为90 s。

综上分析，飞轮储能响应速度快，其运行特性与飞轮的转速呈正相关，因此用户在使用飞轮储能与电网进行互动时，需充分考虑飞轮的转速阈值。

2.3 电动汽车仿真

将1.3节中3种电动汽车充放电模型分别命名为模型1、模型2和模型3，采用Monte Carlo算法对3个模型进行迭代计算，迭代次数为1 000次。单台电动汽车单日内充放电功率曲线如图7—9所示。

图7 单台电动汽车充电功率需求（模型1）Fig.7 Charging power demand of a single electric vehicle（model 1）

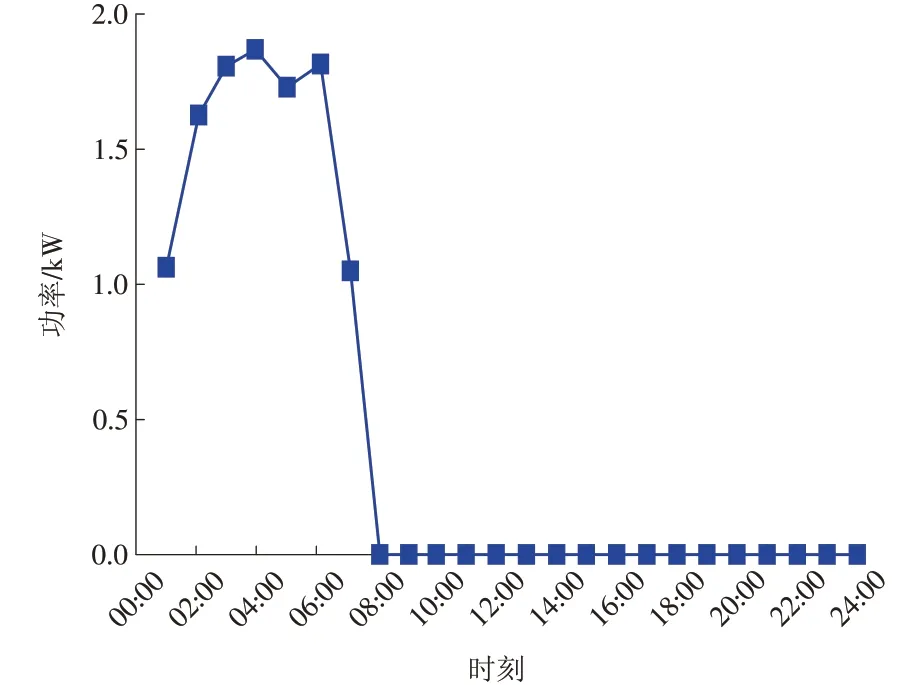
图8 单台电动汽车充电功率需求（模型2）Fig.8 Charging power demand of a single electric vehicle（model 2）

由仿真结果可见，模型1 和模型2 中电动汽车均只有充电需求，且有明显的时间特点。模型1 中电动汽车的充电需求从11：00开始逐渐上升，19：00到达顶峰后逐渐降低；模型2 中电动汽车主要在用电谷期（01：00—08：00）进行充电，其他时间段无充电行为。模型3中电动汽车既有充电行为也有放电行为，放电主要集中在午高峰和晚高峰时期，充电行为则与模型2类似，集中在用电谷期，对电网运行来说是一种良好的用电模式。

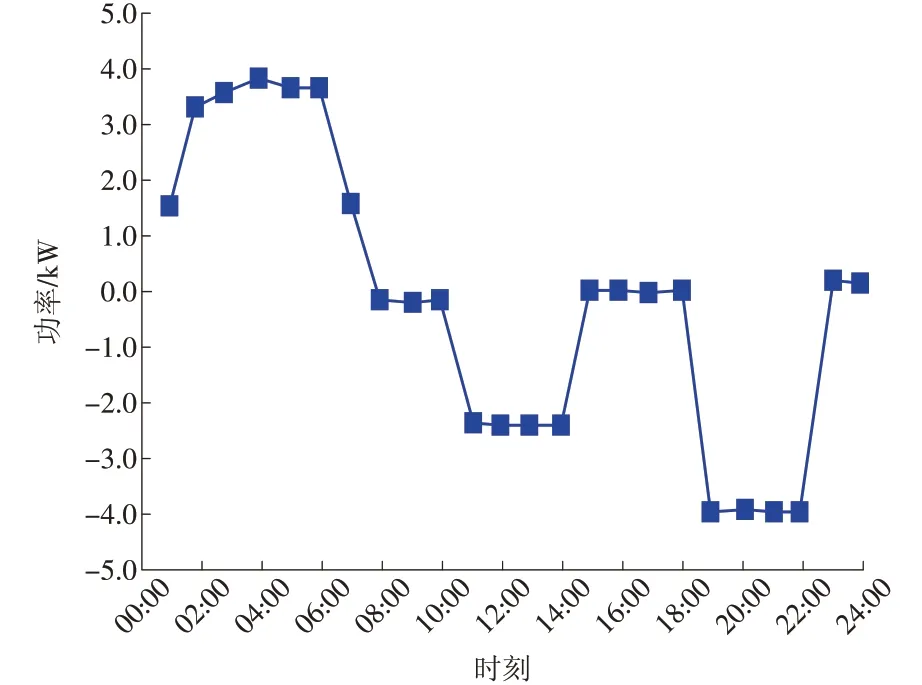
图9 单台电动汽车充电功率需求（模型3）Fig.9 Charging power demand of a single electric vehicle（model 3）

3 结论

选取具有储能作用的用户侧负荷，对其供用能特性进行分析。分别建立蓄电池、飞轮储能和电动汽车的仿真模型，分别通过物理试验和软件仿真模拟其实际运行情况，根据试验数据可以得到典型供用能负荷的运行特性。

（1）蓄电池有良好的运行性能，充电时即使充电电压较低，蓄电池仍能保持良好的充电速度；放电时，在绝大部分放电期内端电压变化较小。同时，研究了温度对于蓄电池充放电的影响，即充电电压随温度升高呈现下降趋势，放电容量随温度升高而增大。由于其优秀的运行特性，蓄电池已广泛应用于工业、交通航海、航天、新能源储能等领域。

（2）飞轮储能响应速度快，损耗小，其运行特性与飞轮的转速呈正相关，因此在使用飞轮储能时需要充分考虑飞轮的转速阈值。基于其运行特点，飞轮储能可应用于城市地铁和电气化铁路牵引变电所等领域。

（3）电动汽车的运行特性灵活多样，具有巨大的应用潜力，可用于需求响应项目，是负荷侧参与电网调节的重要资源。

这些典型供用电负荷的运行特性分析可为后续进一步研究具有储能作用的用户侧负荷在需求响应中的作用提供参考。