基于社区划分的GRU神经网络负荷建模

赵省军，张开鹏，付鑫权，司英莲，刘志栋*，周登钰

（1.国网甘肃省电力公司武威供电公司，甘肃武威 733000；2.西华大学电气与电子信息学院，成都 610039）

0 引言

电力系统仿真是分析研究、调度运行电力系统的主要手段。负荷模型的准确性会直接影响电力系统的仿真结果，从而对电力系统运行、控制、调度等决策造成影响。因此，建立准确、有效的电力负荷模型对电力系统仿真分析十分必要［1］。近年来，电力系统中的负荷成分也在不断变化，各种非线性负荷占比与日俱增，大量分布式电源并入配电网，因此精确的负荷建模对提高电力系统数字仿真精度尤为重要［2-3］。

现有的负荷建模方法可以归纳为机理性建模和非机理性建模。机理性建模通过函数模型和多项式模型对静态负荷进行线性表达，并通过感应电动机模型或感应电动机与零膨胀泊松回归（Zeroinflated Poisson，ZIP）模型并联的简化电路模型表达部分动态负荷。机理性模型在应对分布式电源与各种非线性负荷大量接入配电网时，会出现准确性过低或模型结构复杂、参数过多等问题［4-5］。

非机理性建模包括常微分方程模型、传递函数模型、状态空间模型、时域离散模型和考虑负荷非线性特性而提出的人工神经网络模型。近年来，随着机器学习的不断发展，各种神经网络模型被应用到负荷建模中。文献［6］和文献［7］通过引入径向基函数（Radial Basic Function，RBF）神经网络，对含有不同比例的分布式电源接入节点进行负荷建模，模型精度较高。但是该方法应用于配电网所有节点统一建模时效果欠佳。文献［8］将节点一年内每天负荷曲线进行聚类，对全年该节点每类的典型负荷曲线进行神经网络负荷建模。但节点数量的增加导致负荷类型增加，会出现模型复杂、参数过多等问题。文献［9］详细阐述了长短期记忆（Long Short Term Memory，LSTM）递归神经网络（Recurrent Neural Network，RNN）在负荷建模中的适用性，利用LSTM 网络的时序记忆功能，对电力系统中时序数据进行有效建模。但LSTM 网络存在参数较多、模型收敛速度较慢等问题。

门控循环单元（Gated Recurrent Unit，GRU）是一种基于LSTM 的优化网络［10］，简化了LSTM 网络的内部单元结构，故其在保证较高精度的同时能够有效缩短模型的训练时间，更加适用于建立负荷模型。文献［11］提出将GRU 神经网络引入负荷建模领域，对现代电网分布式电源与非线性负荷的接入具有很强的适应性，建立的非机理模型能够精确地得到系统的负荷值。现有的负荷建模并没有考虑电网拓扑结构，只是对单一的节点进行建模。而电力系统作为典型的复杂网络系统，且在配电网节点数越来越多的情况下，只考虑单一节点的负荷建模方式适用性较差。为实现电网运行状态在线监控及调度决策的快速制定，对配电网进行区域划分，实行“分而治之”，有效减少负荷模型的数量，提高计算速度，减小电网状态分析及调度策略制定的复杂程度［12-14］。

综上所述，提出了基于社区划分的GRU 神经网络负荷建模方法。主要创新点和优势在于：利用社区分类算法，将配电网分成各节点联系紧密的若干社区，再分别对社区进行建模，解决了配电网节点数过多情况下负荷模型复杂、计算效率低等问题。同时，基于GRU 神经网络的等效负荷建模方法能够充分兼顾数据的时序性和非线性关系，有效反映时间序列数据中的长期历史过程。最后，为了考虑社区内部各节点的拓扑结构，模拟重要节点在实际网络中的影响程度更大，引入节点度中心性作为网络输入特征量。

1 社区划分

社区划分的基本思路为：同一社区内节点之间的连接更紧密，而不同社区之间的连接比较松散。文献［15］提出的加文-纽曼（Girvan-Newman，GN）算法是一种最典型的社区分裂方法。GN 算法的重要概念为边介数（Betweenness），即网络中任意2 个节点通过此边的最短路径的数目。具体算法思路为，在网络之中，通过社区内部的边的最短路径相对较少，而通过社区之间的边的最短路径的数目则相对较多。GN 算法是基于删除边的算法，本质是基于聚类中的分裂思想，在原理上使用边介数作为相似度的度量方法。在GN 算法中，每次都会选择并删除边介数高的边，网络分裂速度远快于随机删除边时的网络分裂。

GN算法的步骤如下。

（1）计算每一条边的边介数。

（2）删除边介数最大的边。

（3）重新计算网络中剩下的边的边介数。

（4）重复（3）和（4）步骤，直到网络中的任一顶点作为一个社区为止。

为了定量描述社区划分的好坏，提出了模块度的概念，对社区进行模块化描述。事实上，基于模块化优化的社区划分算法就是将质量函数Q最大化，从而得到更好的社区划分。质量函数Q 的得分越高，发现的群落结构与客观事实越一致。质量函数Q定义为

式中：Q为质量函数；m为图的边数；A为图的邻接矩阵；ki为节点i的度；δij=1时，节点i和节点j在同一社区；δij=0时，节点i和节点j不在同一社区。

2 GRU神经网络

文献［16］使用LSTM 网络搭建主动式配电网的等效模型，将电力系统单个节点实测电压作为1 个LSTM 隐藏层和2 个全连接（Fully Connected，FC）层隐藏层构成的神经网络的输入，并将该节点的有功功率和无功功率作为输出。这种对于单个节点的建模方式，在大规模电力系统中很难实行，会导致模型过多、参数复杂、效率低等问题。针对这一问题提出考虑整个电网所有节点的等效负荷模型，需要使用更加优化的神经网络模型，因此引入GRU 神经网络。GRU基本单元如图1所示。

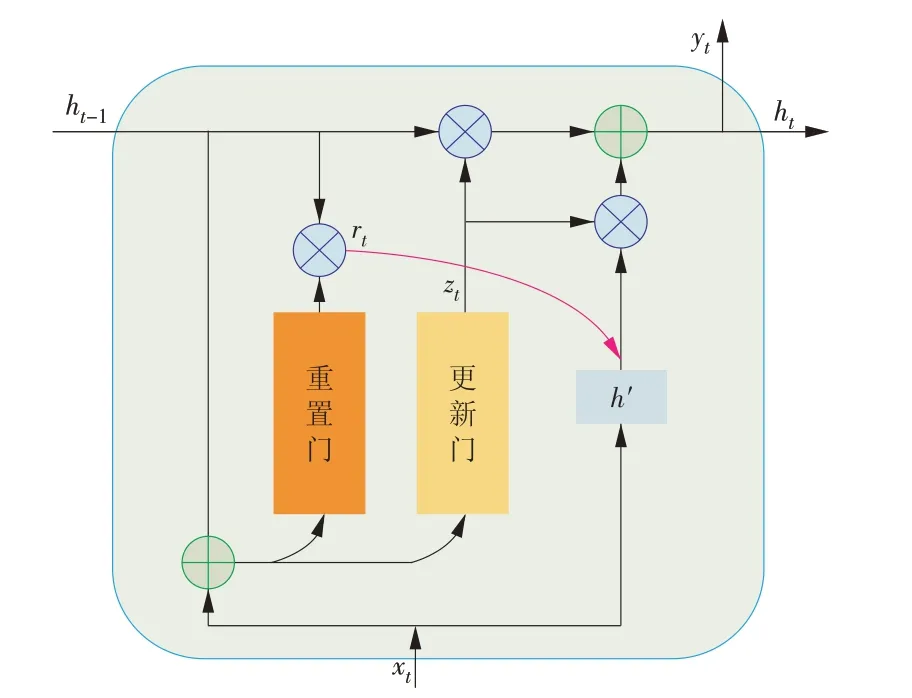
图1 GRU基本单元Fig.1 GRU basic unit

GRU 神经网络是在LSTM 及RNN 循环神经网络的基础上，对神经元内部的组成结构进行了优化，可以显著提升模型训练的效率。文献［17-18］将GRU 神经网络引入电力系统负荷预测，充分考虑负荷的时序特性，训练速度快，预测精度高。GRU网络的前向传播公式为

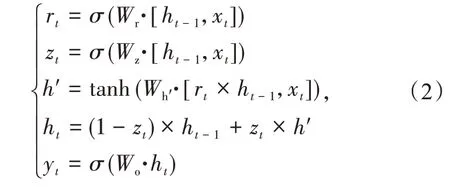
式中：xt为输入向量；ht-1为上一时刻的状态变量；ht为当前时刻的状态向量；zt为更新门的状态；rt为重置门的状态；h′为当前候选集的状态；yt为当前时刻的输出向量；Wr为更新门与z及ht-1构成的连接矩阵相乘的权重参数；Wz为重置门与z及ht-1构成的连接矩阵相乘的权重参数；Wh′为候选集与z及ht-1构成的连接矩阵相乘的权重参数；Wo为输出向量与z及ht-1构成的连接矩阵相乘的权重参数；［］表示向量连接；·表示矩阵点乘；×表示矩阵乘积；σ(x)表示sigmoid激活函数；tanh(x)则为tanh激活函数。σ(x)及tanh(x)的公式为

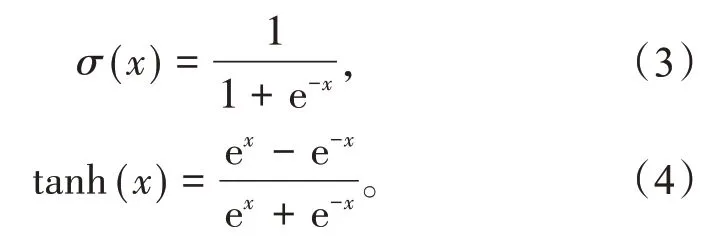
GRU 神经网络以更新门和重置门作为核心模块，输入变量xt和上一时刻的状态记忆变量ht-1的拼接矩阵经sigmoid 非线性变化后输入到更新门中，决定上一时刻状态变量被带入到当前状态中的程度。重置门控制上一时刻被写入到候选集的信息量，通过1-zt倍的ht-1存储上一时刻的信息，并通过zt倍的h′记录当前时刻的信息，再将二者相加的结果作为当前时刻的输出值。

3 GN-GRU等效负荷模型

3.1 总体模型

GN-GRU 等效模型基于大电网拓扑结构原理，使用GN算法对社区进行分类，将大电网分为n个独立的社区，并单独对每个社区进行负荷建模。将社区内所有节点的实测电压增量以及前一时刻的有功功率、无功功率实测数据加上各个节点在社区中的度中心性作为GRU 神经网络的输入数据，将当前时刻有功功率、无功功率作为输出数据，用于训练神经网络，得到由n个GRU 模型组成的负荷模型集合，如图2所示。

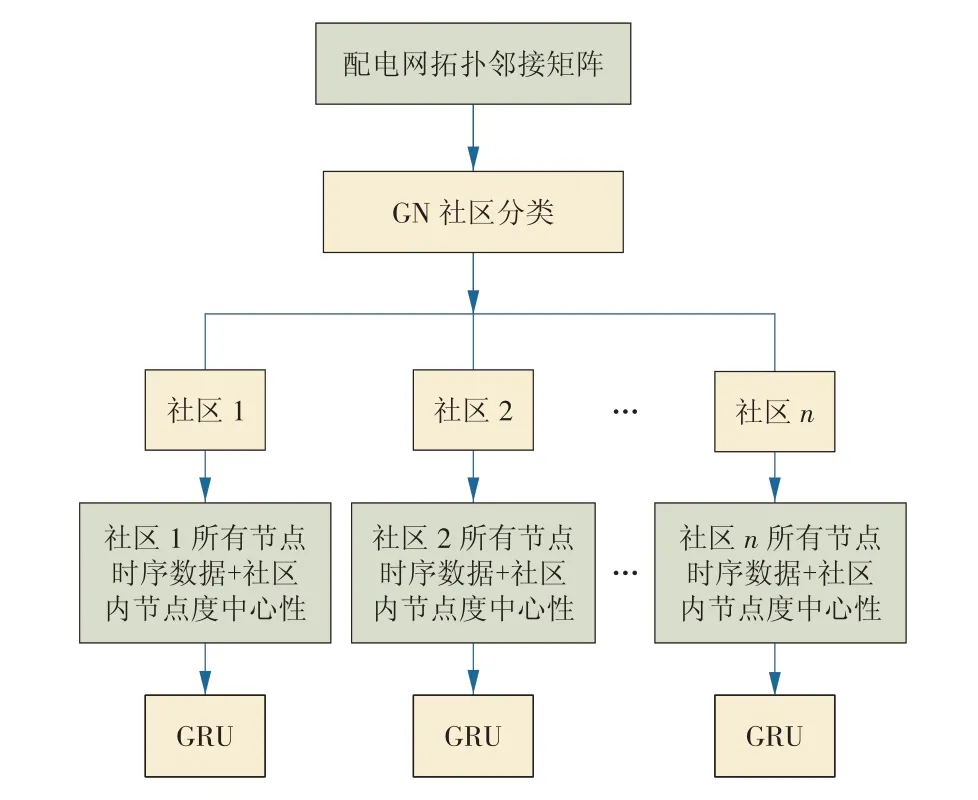
图2 GN⁃GRU等效模型Fig.2 GN⁃GRU equivalent model

3.2 度中心性

度中心性（Degree Centrality）是在网络分析中刻画节点中心性（Centrality）的最直接度量指标。一个节点的节点度越大就表示这个节点的度中心性越高，该节点在网络中就越重要。

在配电网这样的无向图中，度中心性量测网络中某个节点与其他所有节点相联系的程度，其公式为

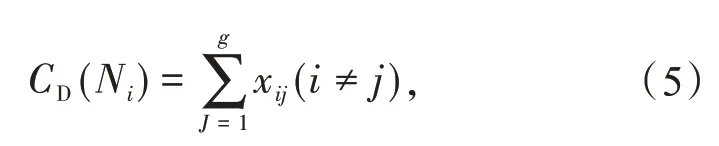
式中：CD(Ni)表示节点i的度中心度，g表示整个无向图的节点数，xij表示i节点与j节点的连接关系（xij=1表示直接相连，xij=0表示未直接相连）。

为消除网络规模变化对度中心性的影响，提出了一个标准化的量测公式

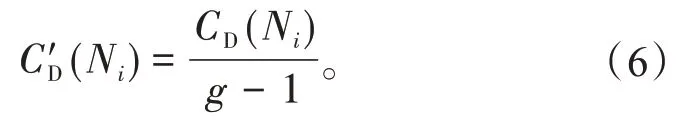
在公式中，使用节点i的度中心性值除以其他g-1个节点最大可能的连接数，得到与节点i有直接联系的网络节点的比例。

3.3 输入特征集的构建

对大规模电力系统进行社区分类，分别对各个社区进行基于节点中心性的GRU 等效负荷建模，将各节点实测电压、上一时刻有功功率、无功功率以及该节点的度中心性作为神经网路的输入，将实测有功、无功作为输出，等效公式为

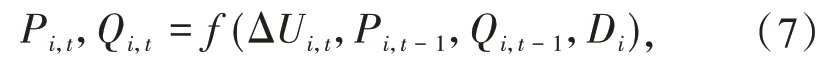
式中：Pi，t和Pi，t-1表示第i个节点t时刻和t-1时刻的实测有功功率；Qi，t和Qi，t-1表示第i个节点t时刻和t-1 时刻的实测无功功率；ΔUi，t-1表示i个节点t时刻的实测电压增量；Di表示第i个节点在社区中的度中心性。

对社区内部所有节点进行负荷等效建模，需要建立具有社区电网特性的神经网络输入特征集，构建输入向量数据Xt为

将实测有功功率、无功功率作为输出值，输出向量数据Yt为

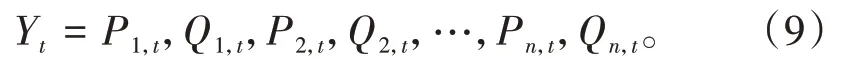
采用均方根误差（RMSE）作为指标，以评估GRU 等效模型的输出与社区电网实测有功功率及无功功率，RMSE方程式为

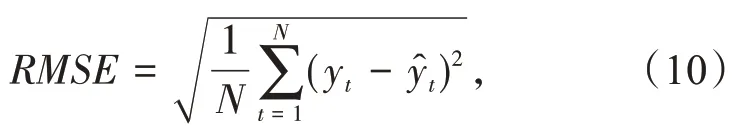
式中：N为输入时序数据总数；yt为社区电网中节点测试有功功率、无功功率，kW为GRU等效模型输出值。

4 案例仿真

4.1 试验环境配置

本仿真模型采用Python 3.7 作为编程语言，软件构架基于Tensorflow，Keras，Scikit‑learn算法框架。配图采用matplotlib 绘图模块绘制。仿真环境采用Intel（R）Core（TM）i5-8250U 处理器，Intel（R）UHD Graphics 962 显示适配器。

4.2 确定网络构架超参数

需要确定的GRU神经网络训练超参数包括GRU网络层数D及Dense网络层数d。采用sigmoid激活函数及Adagrad优化器，初始学习率lr=0.1。

对神经网络进行训练时，设置周期数epochs=50，批次数batch_size=4。采用控制变量法对GRU网络层数D及Dense网络层数d进行最优选择，结果见表1，选择D=3，d=3作为最优神经网络超参数值。

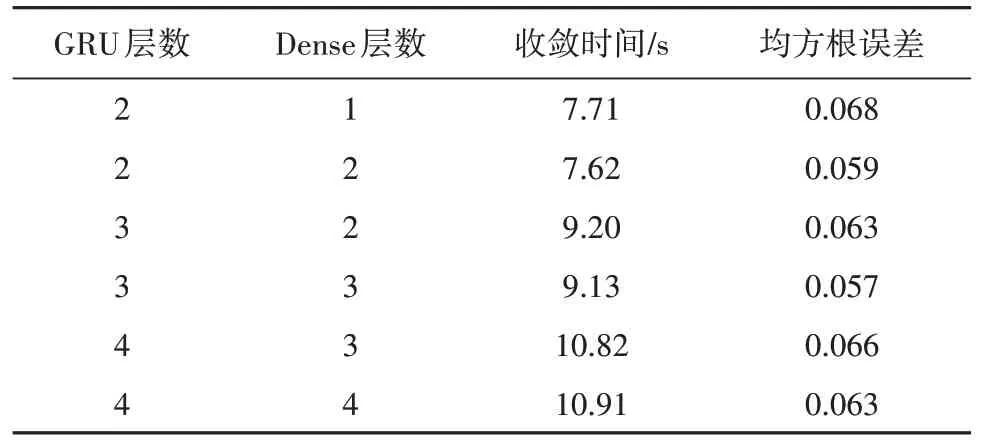
表1 不同层数组合的收敛时间和均方根误差Table 1 Convergence time and root mean square error of the combination with different layers

4.3 仿真结果

为验证提出模型的准确性，选取某40节点配电网作为仿真对象，并将该配电网192 d 负荷数据作为数据集。按照2∶1的比例将数据集划分训练集和测试集，其中训练集为128 d，测试集为64 d，每天96点采样数据。

对GN-GRU 神经网络负荷模型进行训练，与整体配电网40 节点GRU 神经网络负荷模型对比。使用GN 算法对40 节点配电网拓扑进行社区划分，其中电网拓扑中联络开关视为处于闭合状态，得到网络节点之间的分区关系如图3 所示。分别对6 个社区进行负荷建模，如图4及图5所示。

图3 40节点配电网社区划分结果Fig.3 Results of community division of the 40⁃node distribution network

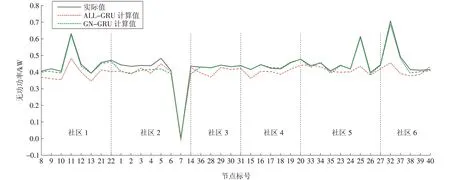
图4 各社区无功功率对比Fig.4 Reactive power of each community

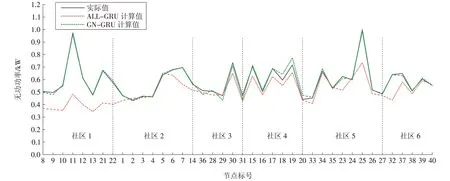
图5 各社区有功功率对比Fig.5 Active power of each community

将每个社区内各个节点的实际值，全部40节点网络进行GRU 神经网络负荷模型（All-GRU）计算结果，以及通过GN-GRU 负荷模型计算结果进行对比。其中All-GRU 模型的输入输出向量与GNGRU的输入输出向量格式相同。

由图4及图5可见，与40节点实际有功功率、无功功率比较，在训练样本相同、模型参数相同的前提下，All-GRU 神经网络负荷模型由于数据维度较高、拟合度较差，导致计算结果较差。在划分社区的情况下，40 个节点有效地划分为节点彼此联系紧密的6个社区，降低了神经网络输入数据维度，且提高了数据之间关联程度。使用6个GN-GRU 神经网络负荷模型对6 个社区分别进行负荷建模，有功功率、无功功率计算结果准确性均较高。

计算上述2个模型的测试集，结果见表2。由表2可见，GN-GRU 负荷模型中6个社区负荷模型得到的平均均方根误差为0.035，明显低于对40 节点配电网整体进行建模的误差结果0.057。由于网络参数的减少，GN-GRU 负荷模型中6 个社区负荷模型平均训练时间小于All-GRU 模型训练时间。综上所述，GN-GRU 模型计算精度提升且计算速度更快，相对于单个节点分别进行建模以及全部节点统一建模的2种情况，该建模方法拥有模型数量少、计算速度适中、计算精度高等优点。GN-GRU 负荷建模方法更加适用于如今规模不断扩大的配电网现状，能够更加快速、有效地计算出电网负荷数据结果。

表2 负荷模型结果对比Table 2 Comparison results of load models

5 结论

提出基于GN-GRU 神经网络的负荷建模方法，首先采用GN 算法对大规模配电网系统进行社区划分；再考虑大规模配电网中每个节点在电网拓扑网络中的度中心性，作为输入特征量；最后采用GRU神经网络依次对每个社区网络进行负荷建模，得到大规模配电网负荷模型集，具有以下优势。

（1）面对现今大规模配电网节点过多、结构复杂等问题，通过GN 社区分类算法，将配电网划分为具有自联系的若干个社区，并分别进行建模，有效减少模型数量，提高计算效率且增加计算精度。

（2）考虑了每个节点的度中心性，将节点在社区网络中的重要性作为输入特征量，能够较真实地反应现实电力系统中重要节点功率变化所带来的同心松弛效应。

（3）使用GRU 作为神经网络主要的单元，能够有效地考虑输入数据中电压值的时序特性。具有较高的计算精度。