基于拓扑重构与分布式电源调度的配电网灾后恢复策略

王卓容，石庆鑫

（华北电力大学电气与电子工程学院，北京 102206）

0 引言

近年来全球气候变化导致极端天气频发，给国内外的电力系统乃至社会经济造成了严重的损失。例如，2017 年发生在美国的哈维、艾玛、玛利亚台风引发了城市配电网的大规模停电，共造成2 000 亿美元经济损失［1］。2021 年河南郑州的7·20 水灾，共造成479 条10 kV 线路停运，1.24 万个配电台区不同程度停电［2］。为了评估配电网抵御小概率、后果严重的自然灾害的能力以及灾后恢复供电的能力，学术界与工业界共同提出了弹性电网的概念，并发展成为一个重要的研究方向［3］。

衡量配电网弹性的指标包括切负荷的经济损失与系统恢复供电的时间［4］。近年来，国内外学者针对提升配电网弹性做了大量工作。主要方法可以总结为3 个方面：一是加固关键的配电网杆塔以降低其因灾损毁坏的概率［5］；二是建设更多的备用线路，当某些线路发生故障时，通过拓扑重构来保证网络的连通性［6-9］；三是在配电网关键负荷附近安装分布式电源，在灾后电网成为孤岛时形成微网，以供应本地重要负荷。一般地，分布式电源包括分布式柴油发电机（Distributed Generator，DG）、光伏（Photovoltaic，PV）发电系统、电池储能系统等［10-11］。

文献［11］将配电网的运行模式分为“常规模式”与“自恢复”模式；在“自恢复”模式中，系统被分割为若干个依赖DG 供电的微网。文献［12］采用改进的维特比算法优化了系统的拓扑重构方案，但未考虑多种分布式电源的最优调度。文献［13］提出一种动态微网的形成方法，最大化系统灾后恢复的负荷。文献［14］提出一种基于模型预测控制算法的恢复策略，但该策略只考虑有功功率，忽略了与无功功率和电压的约束，且未能考虑网络拓扑重构。文献［15］提出一种主-从分布式电源调度与拓扑重构方法，使恢复的负荷最大化。文献［16］提出一种两阶段恢复算法，第1阶段确定重构的拓扑，第2 阶段调度DG 和负荷恢复量。文献［17］提出一种两阶段的弹性提升方法，第1 阶段规划远动开关的位置，第2 阶段在现有远动开关的基础上实现减负荷最小化。文献［18］提出一种多时间步长的动态的网络重构方法，每个时间步长进行DG 调度。但是，频繁闭合、开断开关会影响开关元器件的寿命。如果有足够的历史运行数据，可以建立一个基于数据驱动的最优DG 调度策略以提高弹性［19］。总体上讲，以上文献虽然充分利用了DG 为负荷供电，但几乎都是基于以下假设。

（1）调度策略没有充分利用主网为配电网负荷供电。事实上，主网由于冗余度高，负荷节点发生断电的概率通常小于配网。

（2）分布式电源的输出功率足以承担附近的所有负荷。

基于上述分析，本文提出了一种配电网灾后恢复（Post‑disaster Restoration，PDR）策略，提升系统在极端天气（如台风、洪水等）下的弹性。该算法还利用了联络线和不同类型的可调度和不可调度的分布式电源。本文创新点总结如下。

（1）提出一种依赖线性约束条件的最优拓扑重构方法，最大限度地为负荷供电。采用虚拟网络方法，保证配电网拓扑重构过程中保持辐射状结构。

（2）故障后最优分布式电源调度考虑了不同资源的协同运行，包括可调度的柴油发电机、不可调度的PV 发电系统、需求响应以及具有电压调节功能的器件，如并联电容器。

1 配电系统运行特点

配电系统通常由一条或几条馈线组成，每条馈线都有几条支路。系统的保护装置是基于辐射状拓扑结构设计的，每条馈线都安装了常闭分段开关，并有几个常开开关连接馈线的末端。

极端天气事件发生后，由于线路故障，馈线的某个部分可能形成孤岛。闭合与之相连的备用线路可将这个孤岛连接到另一条馈线，并且调度分布式电源为附近负荷供电，使切负荷的损失最小化［6］，而新的拓扑结构在损坏的线路修复之前保持不变，这种操作方式叫做配电网拓扑重构。一般情况下，存在多种重构方法保证系统的辐射状结构。因此，PDR 的目的是找出最优的网络拓扑，使系统修复期间的运行成本最低。

2 配电网灾后恢复策略

2.1 目标函数

目标函数主要包含2 个部分，第1 部分是切负荷的补偿费用，第2 部分为可调度分布式电源的运行费用，且假设光伏系统的运行成本为0。在调度周期内，网络拓扑保持不变。在极端天气条件下，供应更多的电力负荷（减少缺供电量）比减少费用更重要。为了在极端事件中分布式电源持续时间更长，维持最低成本的分布式电源运行，所以目标函数中也包含了可调度分布式电源的成本，其表达式为

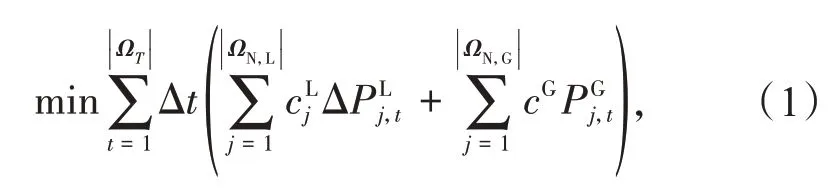
式中：t，ΩT分别为时间指标和时间集合；j，ΩN，L，ΩN，G分别为节点指标、负荷节点集合、发电机节点集合；|·|表示集合中的元素个数；为节点j的切负荷费用；为节点j在t时段的切负荷量；cG为柴油发电机的运行费用；为位于节点j的柴油发电机在t时段的输出功率。

2.2 拓扑重构约束

在图论中，无环连通图称为树［20］，在电力系统中被称为“辐射状网络”。当线路发生故障时，调度中心需要考虑到线路的功率限制，重新形成一个新的、最优的辐射状拓扑结构，使切负荷的量达到最小。此处引入了一个与原始电网具有相同拓扑结构和开关状态变量zij的无损虚拟网络，如图1 所示［15］。在这个虚拟网络中，假设每个非源节点的负荷为1.0，则辐射状拓扑的约束为式（2）—（7）。

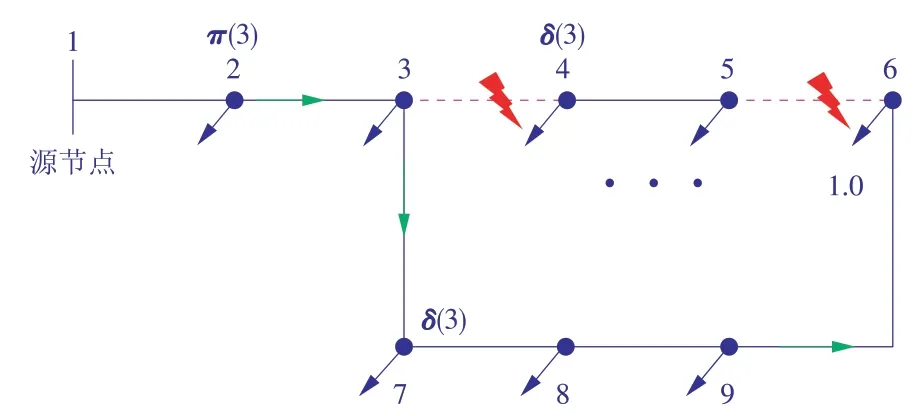
图1 偶然故障发生后部分连接网络示意Fig.1 Example of a partially⁃connected network after a contingency

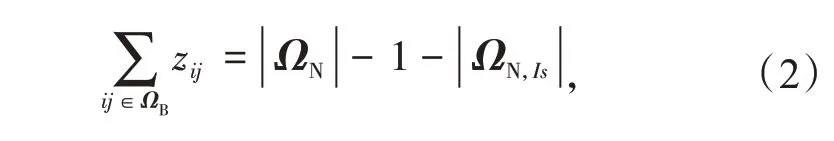
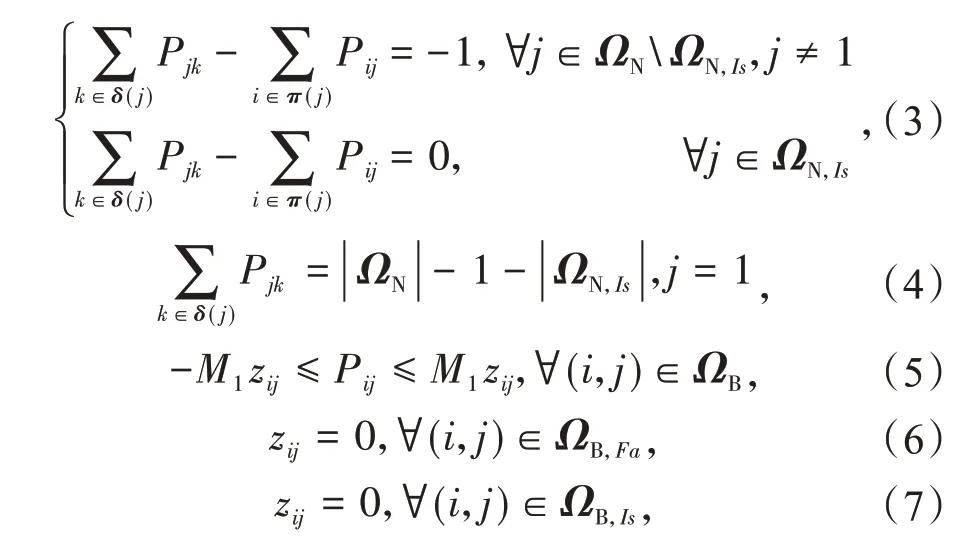
式中：zij为开关状态（1-闭合，0-断开）；ΩN为节点的集合；ΩN，Is为孤岛节点的集合；π（j）为节点j的相邻上游节点集合；δ（j）为节点j的相邻下游节点集合；Pjk为线路（j，k）的功率；Pij为线路（i，j）的功率；ΩB为线路的集合；ΩB，Fa为故障线路的集合；ΩB，Is为孤岛中线路的集合。

约束（2）表示闭合线路的数量等于非源节点的数量减去孤岛节点的数量。孤岛节点指在所有线路闭合的情况下，此节点与源节点没有连接路径。约束（3）表示每个节点的功率平衡，其中孤岛节点的负荷为0。约束（4）表示与源节点直接相连线路的功率。约束（5）是基于大M法的线路潮流约束，其中，M1是个足够大的常数［21］。若zij=0，则流过线路（i，j）的功率为0。约束（6）表示故障线路被远动开关断开后，在被修复之前保持开路。约束（7）表示这个虚拟网络中的孤岛线路无法与主网联通，因而功率为0。

2.3 系统运行约束

一般而言，柴油发电机发1 kW·h电的成本高于从电力市场购电的费用。因此，本文假设只有在发生N-k 故障时才使用可调度的分布式电源。PDR算法受到设备运行约束和系统潮流约束。

系统运行约束为式（8）—（23）。由于此类约束条件均与时间有关，为简单起见，每个等式后都省略了表达式∀t∈ΩT。

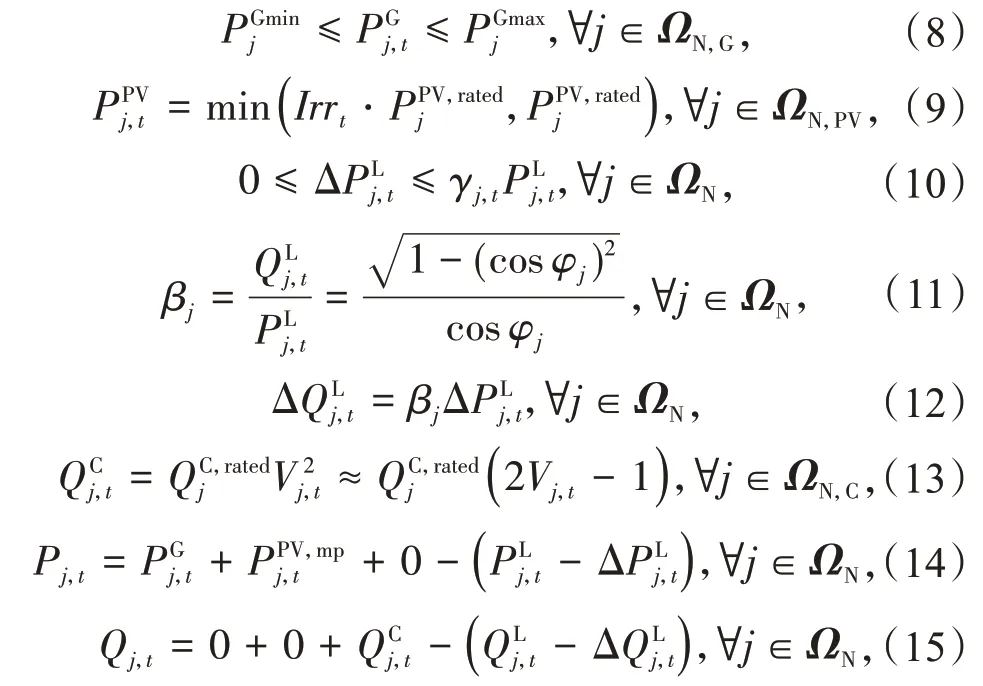
约束（8）表示柴油发电机的出力上下限，其出力可调度。约束（9）表示光伏发电系统始终在最大功率点运行，因此在正常范围内输出功率与光照强度成比例关系。约束（10）表示切负荷的上下限，其中可以通过历史负荷曲线来预测。约束（11）—（12）表示有功功率和无功功率的比值。为简化计算，本文假设负荷的功率因数始终恒定。旁路电容器（Shunt Capacitor，SC）的无功功率输出与电压平方成正比。由于节点电压在很窄的范围内波动，SC 无功出力与电压的关系式可以线性化，如式（13）所示。约束（14）—（15）表示节点j注入有功、无功功率的平衡方程，包括发电机输出、光伏系统输出以及切负荷后的负荷需求。综合考虑以上公式，节点有功功率和无功功率表示为式（16）—（17）。注：光伏系统的无功输出、DG 的无功输出以及电容器的有功输出均设置为0，则2个等式具有相似的形式。

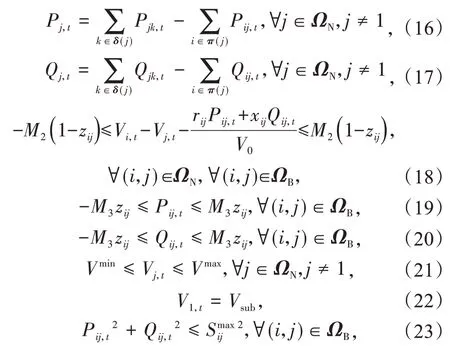
式中：Pij，t，Qij，t为t时段线路（i，j）流过的有功、无功功率；Vi，t为t时段母线i的电压幅值；rij，xij为线路（i，j）的电阻和电抗；Vmax，Vmin为电压的上、下限；M2和M3为足够大的常数；为线路（i，j）容量的最大值。

约束（16）—（17）表示节点j的有功与无功功率的平衡。约束（18）为基于线性化Distflow 模型的潮流约束［19］。V0表示额定电压，通常设为1。若zij=1，则不等式约束转化为等式约束，表示电压降落Vi-Vj由线路潮流所决定。若zij=0，则电压约束Vi-Vj松弛。约束（19）—（20）表示如果线路（i，j）断开，则此线路上没有功率。约束（21）为负荷节点的电压上下限。通常将变电站节点设置为平衡节点，如式（22）所示。约束（23）可以用P-Q坐标系下的一个圆表示，如图2所示，圆的边界可以近似为一个外接多边形。因为在电力系统中，通常有|Qij，t|≤|Pij，t|，所以非线性约束（23）可以等效为式（24）—（26）这3个分段线性方程。

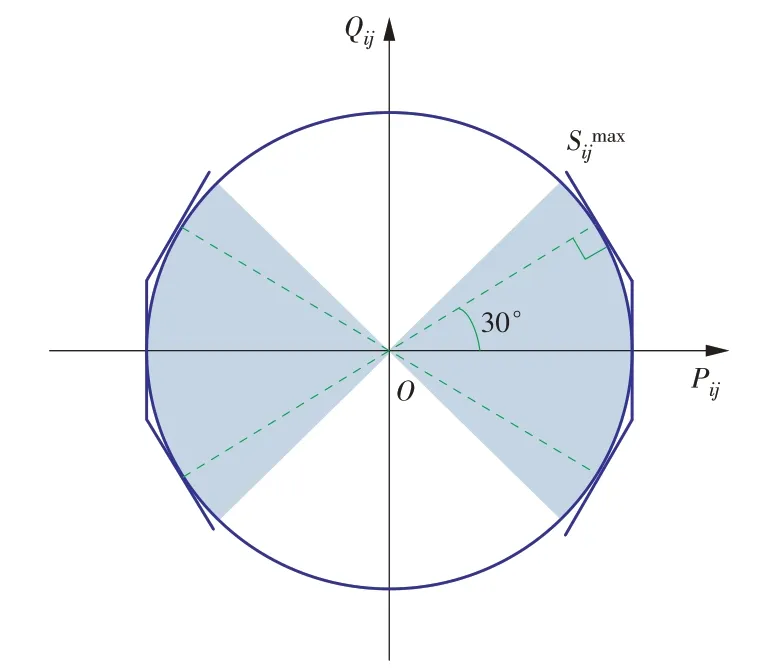
图2 线路功率限制的分段线性化示意Fig.2 Piece⁃wise linearization of line power limit

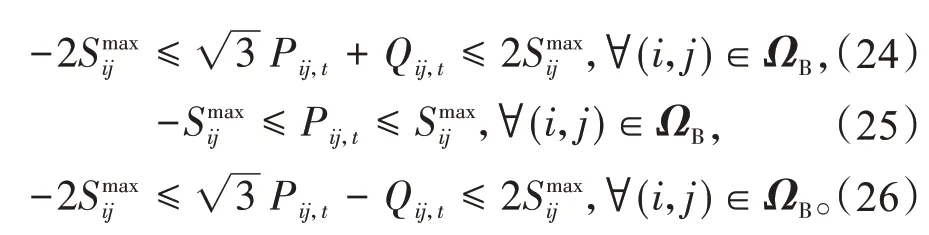
2.4 PDR方法概述

由于所有的约束都是线性的或线性化的，整个PDR 方法建模为混合整数线性规划（MILP）。根据2.3节的讨论，优化模型总结如下。

目标函数：式（1）；

约束条件：式（2）—（22），式（24）—（26）；

在PDR 方法中，目标函数为最小化切负荷的补偿费用与柴油发电机的运行费用，约束条件包括拓扑重构约束与系统运行约束。其中，系统运行约束由发电机输出约束、切负荷上下限约束和线路潮流约束组成。

3 算例分析

本节以IEEE 33 节点系统为例验证所提灾后调度策略。计算环境为具有英特尔酷睿i7 处理器（2.8 GHz）电脑。编程由MATLAB 实现，优化程序包为IBM ILOG CPLEX Optimization Studio V12.8.0。

包含分布式电源的33 节点系统如图3 所示，IEEE 33 节点系统包含了多条支路，实线表示常闭线路，虚线表示联络线，也即常开线路；1 号节点为变电站节点，负荷分为重要负荷与非重要负荷，分别用不同颜色标注；分布式电源分为可调度的柴油发电机与不可调度的光伏发电系统；部分节点安装有旁路电容器。此外，假设1 号节点至6 号节点之间的线路为地下电缆，不会因极端天气而受损。系统的主要参数见表1。优化时间步长∆t为1 h，假设所有线路故障在第10 h 发生，在第22 h 得到完全修复。重要负荷和非重要负荷分别采用不同的日负荷曲线。基于预测的日负荷曲线与光照强度曲线，首先计算正常运行状态下的24 h潮流。

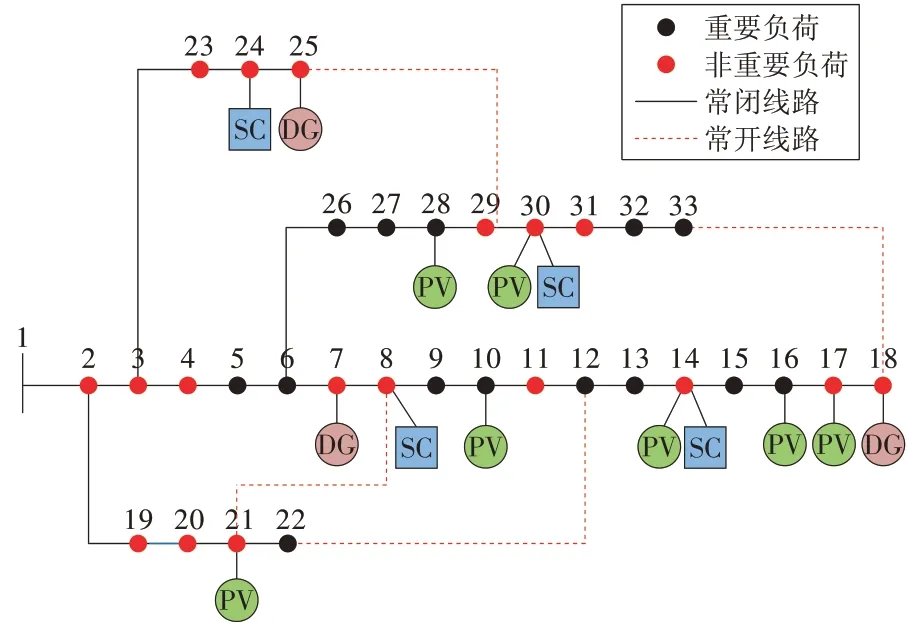
图3 包含分布式电源的33节点系统Fig.3 IEEE 33⁃bus system with DGs

表1 33节点系统相关参数Table 1 Parameters of the IEEE 33⁃bus system

为了充分验证所提方法的作用，本节选取切负荷较严重的2个典型N-k故障场景。

场景1：线路（12，13）和线路（27，28）断开。

场景2：线路（9，10），（23，24）和线路（6，26）断开。

针对每个场景求解PDR 优化模型，主要优化结果见表2。2 个场景网络重构的结果如图4 所示。在2 种场景中，均闭合多个联络开关以保证供电中断的负荷重新供电，同时断开分段开关以避免网络形成环状结构。分布式电源和负荷的响应如图5所示，包括柴油发电机的功率输出、所有重要负荷与非重要负荷的功率。

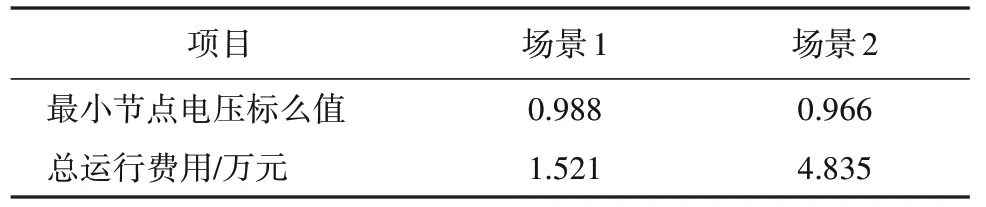
表2 两个场景的主要计算结果Table 2 Major results of the two scenarios

图4 网络重构结果Fig.4 Network reconfiguration

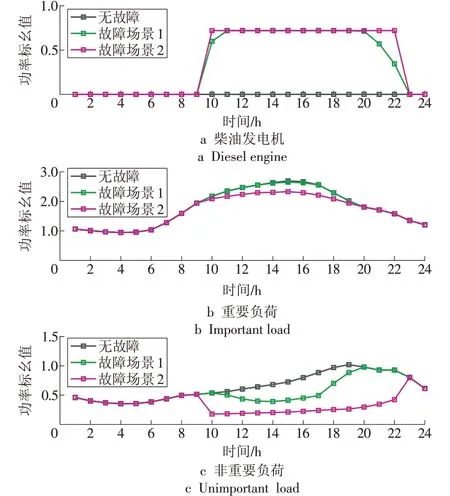
图5 分布式电源和负荷响应Fig.5 DGs and demand responses

场景1 中，2 条线路故障使节点28—33，13—18均形成孤岛；此时通过联络线使孤岛负荷转移至线路（23，24）与（2，19）；然而，由于线路（2，19）容量有限，需要启动柴油发电机，并切除部分负荷；PDR 选取非重要负荷优先切除。场景2 中，多条线路故障导致节点24—25，26—33，10—18 均形成孤岛；此时闭合4条联络线，同时断开线路（20，21）可将孤岛负荷全部连接到线路2，3，…，8中，通过主网供电。线路（21，22）的容量为1 MV·A，重构后由于容量越限导致了大量的减负荷。因此，场景2 的总运行费用较场景1大。

4 结论和展望

本文提出了一种考虑网络重构和分布式电源调度的PDR 策略。利用联络线（常开线路）和可调度分布式电源来降低缺供负荷，特别是优先保障重要负荷的供电。本文主要贡献有以下2点。

（1）提出了一种改进的虚拟网络的方法，将具有孤岛的网络在重构中辐射状约束转化为一种线性约束。

（2）提出了一种包含可调度分布式电源、不可调度光伏系统和恢复后电压调节装置的最优调度模型。通过协同调度，实现切负荷损失的最小化。

算例分析结果表明，在所有场景下，本文所提PDR 算法能够最大限度地保障负荷供电。与没有使用PDR 算法相比，本文所提PDR 算法通过分布式电源调度与拓扑重构，降低了极端情况下的切负荷损失。不足之处如下。

（1）PDR 算法没有考虑维修人员最优调度的问题。

（2）故障线路被修复后，在修复后的随后几个小时内不投入使用。因此，未来的工作将集中于确定最优序列和对PDR算法进行动态网络重构。